Алгоритмы регрессии - линейная регрессия
Введение в линейную регрессию
Линейная регрессия может быть определена как статистическая модель, которая анализирует линейную связь между зависимой переменной с заданным набором независимых переменных. Линейная связь между переменными означает, что, когда значение одной или нескольких независимых переменных изменится (увеличится или уменьшится), значение зависимой переменной также изменится соответствующим образом (увеличится или уменьшится).
Математически взаимосвязь может быть представлена с помощью следующего уравнения -
Y = mX + b
Здесь Y - зависимая переменная, которую мы пытаемся предсказать.
X - зависимая переменная, которую мы используем, чтобы делать прогнозы.
m - наклон линии регрессии, которая представляет влияние X на Y
b - константа, известная как Y-пересечение. Если X = 0, Y будет равно b.
Кроме того, линейная зависимость может быть положительной или отрицательной по своей природе, как описано ниже -
Положительная линейная связь
Линейная зависимость будет называться положительной, если увеличивается как независимая, так и зависимая переменная. Это можно понять с помощью следующего графика -

Отрицательная линейная связь
Линейная зависимость будет называться положительной, если независимая увеличивается, а зависимая переменная уменьшается. Это можно понять с помощью следующего графика -

Типы линейной регрессии
Линейная регрессия бывает следующих двух типов -
- Простая линейная регрессия
- Множественная линейная регрессия
Простая линейная регрессия (SLR)
Это самая простая версия линейной регрессии, которая предсказывает ответ, используя одну функцию. В SLR предполагается, что две переменные линейно связаны.
Реализация Python
Мы можем реализовать SLR в Python двумя способами: один - предоставить собственный набор данных, а другой - использовать набор данных из библиотеки python scikit-learn.
Example 1 - В следующем примере реализации Python мы используем наш собственный набор данных.
Во-первых, мы начнем с импорта необходимых пакетов следующим образом:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltЗатем определите функцию, которая будет вычислять важные значения для SLR -
def coef_estimation(x, y):Следующая строка скрипта даст количество наблюдений n -
n = np.size(x)Среднее значение вектора x и y можно рассчитать следующим образом:
m_x, m_y = np.mean(x), np.mean(y)Мы можем найти перекрестное отклонение и отклонение относительно x следующим образом:
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xЗатем коэффициенты регрессии, т.е. b, можно рассчитать следующим образом:
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)Затем нам нужно определить функцию, которая будет строить линию регрессии, а также предсказывать вектор ответа -
def plot_regression_line(x, y, b):Следующая строка сценария отобразит фактические точки как диаграмму рассеяния -
plt.scatter(x, y, color = "m", marker = "o", s = 30)Следующая строка сценария предсказывает вектор ответа -
y_pred = b[0] + b[1]*xСледующие строки скрипта построят линию регрессии и поместят на них метки:
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()Наконец, нам нужно определить функцию main () для предоставления набора данных и вызова функции, которую мы определили выше -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()Вывод
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788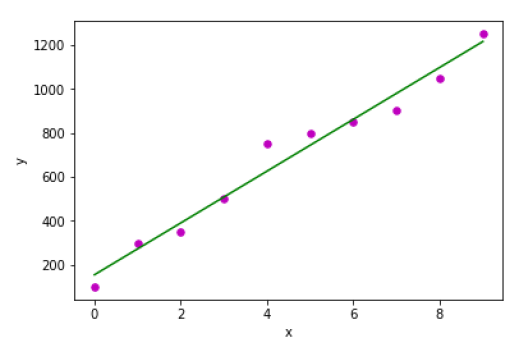
Example 2 - В следующем примере реализации Python мы используем набор данных о диабете из scikit-learn.
Во-первых, мы начнем с импорта необходимых пакетов следующим образом:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreЗатем мы загрузим набор данных о диабете и создадим его объект -
diabetes = datasets.load_diabetes()Поскольку мы внедряем SLR, мы будем использовать только одну функцию, а именно:
X = diabetes.data[:, np.newaxis, 2]Затем нам нужно разделить данные на наборы для обучения и тестирования следующим образом:
X_train = X[:-30]
X_test = X[-30:]Затем нам нужно разделить цель на наборы для обучения и тестирования следующим образом:
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]Теперь, чтобы обучить модель, нам нужно создать объект линейной регрессии следующим образом:
regr = linear_model.LinearRegression()Затем обучите модель с использованием обучающих наборов следующим образом:
regr.fit(X_train, y_train)Затем сделайте прогнозы, используя набор для тестирования следующим образом:
y_pred = regr.predict(X_test)Затем мы напечатаем некоторый коэффициент, такой как MSE, оценка дисперсии и т.
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))Теперь постройте выходы следующим образом:
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()Вывод
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Множественная линейная регрессия (MLR)
Это расширение простой линейной регрессии, которая предсказывает ответ с использованием двух или более функций. Математически мы можем объяснить это следующим образом:
Рассмотрим набор данных, содержащий n наблюдений, p функций, то есть независимых переменных, и y как один ответ, то есть зависимую переменную, линия регрессии для p функций может быть рассчитана следующим образом:
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} $$Здесь h (x i ) - это прогнозируемое значение отклика, а b 0 , b 1 , b 2 …, b p - коэффициенты регрессии.
Модели множественной линейной регрессии всегда включают ошибки в данных, известные как остаточная ошибка, которая изменяет расчет следующим образом:
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} + e_ {i} $$Мы также можем записать приведенное выше уравнение следующим образом -
$$ y_ {i} = h (x_ {i}) + e_ {i} \: или \: e_ {i} = y_ {i} - h (x_ {i}) $$Реализация Python
в этом примере мы будем использовать набор данных о жилье Бостона из scikit learn -
Во-первых, мы начнем с импорта необходимых пакетов следующим образом:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsЗатем загрузите набор данных следующим образом -
boston = datasets.load_boston(return_X_y=False)Следующие строки скрипта будут определять матрицу признаков X и вектор ответа Y -
X = boston.data
y = boston.targetЗатем разделите набор данных на наборы для обучения и тестирования следующим образом:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)пример
Теперь создайте объект линейной регрессии и обучите модель следующим образом:
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()Вывод
Coefficients:
[
-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01
]
Variance score: 0.709454060230326
Предположения
Ниже приведены некоторые предположения о наборе данных, который сделан моделью линейной регрессии.
Multi-collinearity- Модель линейной регрессии предполагает, что в данных очень мало или совсем нет мультиколлинеарности. По сути, мультиколлинеарность возникает, когда независимые переменные или функции имеют в них зависимости.
Auto-correlation- Другое предположение, которое предполагает модель линейной регрессии, состоит в том, что в данных очень мало автокорреляции или она отсутствует. Как правило, автокорреляция возникает, когда существует зависимость между остаточными ошибками.
Relationship between variables - Модель линейной регрессии предполагает, что связь между откликом и характеристическими переменными должна быть линейной.