การออกแบบคอมไพเลอร์ - ตัวแยกวิเคราะห์จากบนลงล่าง
เราได้เรียนรู้ในบทสุดท้ายแล้วว่าเทคนิคการแยกวิเคราะห์จากบนลงล่างจะแยกวิเคราะห์อินพุตและเริ่มสร้างต้นไม้แยกวิเคราะห์จากโหนดรากค่อยๆเคลื่อนลงไปที่โหนดใบไม้ ประเภทของการแยกวิเคราะห์จากบนลงล่างแสดงอยู่ด้านล่าง:
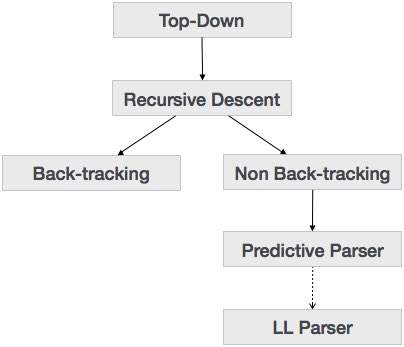
การแยกวิเคราะห์ Descent แบบเรียกซ้ำ
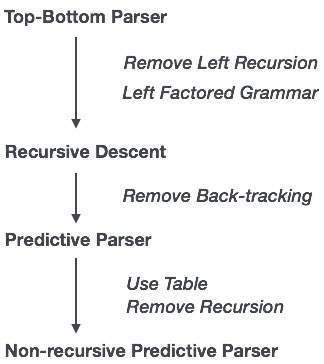
การสืบเชื้อสายซ้ำเป็นเทคนิคการแยกวิเคราะห์จากบนลงล่างที่สร้างแผนผังการแยกวิเคราะห์จากด้านบนและอินพุตจะอ่านจากซ้ายไปขวา ใช้โพรซีเดอร์สำหรับทุกเทอร์มินัลและเอนทิตีที่ไม่ใช่เทอร์มินัล เทคนิคการแยกวิเคราะห์นี้จะแยกวิเคราะห์ข้อมูลที่ป้อนซ้ำเพื่อสร้างโครงสร้างการแยกวิเคราะห์ซึ่งอาจต้องใช้การติดตามย้อนกลับหรือไม่ก็ได้ แต่ไวยากรณ์ที่เกี่ยวข้อง (หากไม่ได้แยกตัวประกอบ) ไม่สามารถหลีกเลี่ยงการติดตามย้อนกลับได้ รูปแบบของการแยกวิเคราะห์การสืบเชื้อสายซ้ำที่ไม่จำเป็นต้องมีการติดตามย้อนกลับเรียกว่าpredictive parsing.
เทคนิคการแยกวิเคราะห์นี้ถือได้ว่าเป็นแบบวนซ้ำเนื่องจากใช้ไวยากรณ์ที่ไม่มีบริบทซึ่งเป็นแบบวนซ้ำ
การติดตามย้อนกลับ
ตัวแยกวิเคราะห์จากบนลงล่างเริ่มต้นจากโหนดรูท (สัญลักษณ์เริ่มต้น) และจับคู่สตริงอินพุตกับกฎการผลิตเพื่อแทนที่ (ถ้าตรงกัน) เพื่อให้เข้าใจสิ่งนี้ให้ใช้ตัวอย่างต่อไปนี้ของ CFG:
S → rXd | rZd
X → oa | ea
Z → aiสำหรับสตริงอินพุต: read ตัวแยกวิเคราะห์จากบนลงล่างจะทำงานดังนี้:
มันจะเริ่มต้นด้วย S จากกฎการผลิตและจะจับคู่ผลตอบแทนกับตัวอักษรซ้ายสุดของอินพุตนั่นคือ 'r' การผลิต S (S → rXd) ที่ตรงกับมัน ดังนั้นตัวแยกวิเคราะห์จากบนลงล่างจะเลื่อนไปยังตัวอักษรอินพุตถัดไป (เช่น 'e') ตัวแยกวิเคราะห์พยายามขยาย 'X' ที่ไม่ใช่เทอร์มินัลและตรวจสอบการผลิตจากด้านซ้าย (X → oa) ไม่ตรงกับสัญลักษณ์อินพุตถัดไป ดังนั้นตัวแยกวิเคราะห์จากบนลงล่างจะติดตามเพื่อรับกฎการผลิตถัดไปของ X, (X → ea)
ตอนนี้โปรแกรมแยกวิเคราะห์จะจับคู่ตัวอักษรอินพุตทั้งหมดตามลำดับ ยอมรับสตริงแล้ว
|
|
|
|
|
Predictive Parser
Predictive parser คือตัวแยกวิเคราะห์การสืบเชื้อสายแบบเรียกซ้ำซึ่งมีความสามารถในการคาดเดาว่าจะใช้การผลิตใดเพื่อแทนที่สตริงอินพุต โปรแกรมวิเคราะห์คำทำนายจะไม่ประสบกับการย้อนรอย
ในการทำงานให้สำเร็จตัววิเคราะห์คำทำนายจะใช้ตัวชี้มองไปข้างหน้าซึ่งชี้ไปที่สัญลักษณ์อินพุตถัดไป ในการทำให้ตัวแยกวิเคราะห์กลับมาติดตามได้ฟรีตัวแยกวิเคราะห์เชิงคาดการณ์จะกำหนดข้อ จำกัด บางประการเกี่ยวกับไวยากรณ์และยอมรับเฉพาะระดับของไวยากรณ์ที่เรียกว่าไวยากรณ์ LL (k)
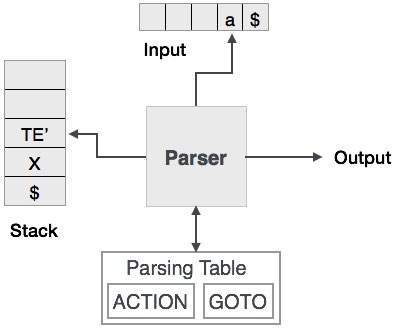
การแยกวิเคราะห์เชิงคาดการณ์ใช้สแต็กและตารางแยกวิเคราะห์เพื่อแยกวิเคราะห์อินพุตและสร้างโครงสร้างการแยกวิเคราะห์ ทั้งสแต็กและอินพุตมีสัญลักษณ์สิ้นสุด$เพื่อแสดงว่าสแต็กว่างเปล่าและอินพุตถูกใช้ไป ตัวแยกวิเคราะห์หมายถึงตารางการแยกวิเคราะห์เพื่อทำการตัดสินใจใด ๆ เกี่ยวกับการรวมองค์ประกอบอินพุตและสแต็ก
ในการแยกวิเคราะห์แบบเรียกซ้ำตัวแยกวิเคราะห์อาจมีการผลิตมากกว่าหนึ่งรายการให้เลือกสำหรับอินสแตนซ์อินพุตเดียวในขณะที่ในการแยกวิเคราะห์เชิงคาดการณ์แต่ละขั้นตอนจะมีการผลิตให้เลือกมากที่สุด อาจมีกรณีที่ไม่มีการผลิตที่ตรงกับสตริงอินพุตทำให้ขั้นตอนการแยกวิเคราะห์ล้มเหลว
LL Parser
LL Parser ยอมรับไวยากรณ์ LL ไวยากรณ์ LL เป็นชุดย่อยของไวยากรณ์ที่ไม่มีบริบท แต่มีข้อ จำกัด บางประการในการรับเวอร์ชันที่เรียบง่ายเพื่อให้สามารถใช้งานได้ง่าย ไวยากรณ์ LL สามารถใช้งานได้โดยใช้อัลกอริทึมทั้งสองแบบคือการสืบเชื้อสายซ้ำหรือการขับเคลื่อนด้วยตาราง
LL parser แสดงเป็น LL (k) L ตัวแรกใน LL (k) กำลังแยกวิเคราะห์อินพุตจากซ้ายไปขวา L ตัวที่สองใน LL (k) ย่อมาจากการได้มาจากซ้ายสุดและ k หมายถึงจำนวนการมองไปข้างหน้า โดยทั่วไป k = 1 ดังนั้น LL (k) จึงอาจเขียนเป็น LL (1)
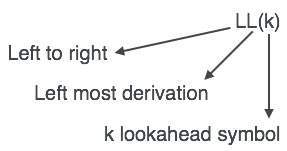
อัลกอริทึมการแยกวิเคราะห์ LL
เราอาจยึดติดกับดีเทอร์มินิสติก LL (1) สำหรับคำอธิบายตัวแยกวิเคราะห์เนื่องจากขนาดของตารางโตขึ้นแบบทวีคูณด้วยค่า k ประการที่สองถ้าไวยากรณ์ที่กำหนดไม่ใช่ LL (1) โดยปกติแล้วจะไม่ใช่ LL (k) สำหรับ k ใด ๆ ที่กำหนด
ด้านล่างนี้เป็นอัลกอริทึมสำหรับการแยกวิเคราะห์ LL (1):
Input:
string ω
parsing table M for grammar G
Output:
If ω is in L(G) then left-most derivation of ω,
error otherwise.
Initial State : $S on stack (with S being start symbol)
ω$ in the input buffer
SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ Vt or $
if X = a
POP X and advance ip.
else
error()
endif
else /* X is non-terminal */
if M[X,a] = X → Y1, Y2,... Yk
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
Output the production X → Y1, Y2,... Yk
else
error()
endif
endif
until X = $ /* empty stack */ไวยากรณ์ G คือ LL (1) ถ้า A →α | βเป็นสองโปรดักชั่นที่แตกต่างกันของ G:
สำหรับไม่มีเทอร์มินัลทั้งαและβได้รับสตริงที่ขึ้นต้นด้วย.
มากที่สุดหนึ่งในαและ der สามารถหาสตริงว่างได้
ถ้าβ→ t ดังนั้นαจะไม่ได้รับสตริงใด ๆ ที่ขึ้นต้นด้วยเทอร์มินัลใน FOLLOW (A)