การสื่อสารแบบดิจิทัล - การมอดูเลตเดลต้า
อัตราการสุ่มตัวอย่างของสัญญาณควรสูงกว่าอัตรา Nyquist เพื่อให้ได้การสุ่มตัวอย่างที่ดีขึ้น หากช่วงเวลาการสุ่มตัวอย่างใน Differential PCM ลดลงมากความแตกต่างของแอมพลิจูดตัวอย่างต่อตัวอย่างจะน้อยมากราวกับว่าความแตกต่างนั้น1-bit quantizationจากนั้นขนาดขั้นตอนจะมีขนาดเล็กมากเช่น Δ (เดลต้า).
การปรับเดลต้า
ประเภทของการมอดูเลตที่อัตราการสุ่มตัวอย่างสูงกว่ามากและขนาดของขั้นตอนหลังจากการหาปริมาณมีค่าน้อยกว่า Δการมอดูเลตดังกล่าวเรียกว่า delta modulation.
คุณสมบัติของ Delta Modulation
ต่อไปนี้เป็นคุณสมบัติบางประการของการมอดูเลตเดลต้า
อินพุตที่สุ่มตัวอย่างมากเกินไปถูกนำมาใช้เพื่อใช้ประโยชน์จากความสัมพันธ์ของสัญญาณอย่างเต็มที่
การออกแบบปริมาณนั้นเรียบง่าย
ลำดับการป้อนข้อมูลสูงกว่าอัตรา Nyquist มาก
คุณภาพอยู่ในระดับปานกลาง
การออกแบบโมดูเลเตอร์และเดโมดูเลเตอร์นั้นเรียบง่าย
การประมาณแบบขั้นบันไดของรูปคลื่นเอาท์พุต
ขนาดขั้นบันไดมีขนาดเล็กมากกล่าวคือ Δ (เดลต้า).
ผู้ใช้สามารถกำหนดอัตราบิตได้
สิ่งนี้เกี่ยวข้องกับการใช้งานที่ง่ายกว่า
Delta Modulation เป็นรูปแบบที่เรียบง่ายของเทคนิค DPCM ซึ่งเรียกอีกอย่างว่า 1-bit DPCM scheme. เมื่อช่วงเวลาการสุ่มตัวอย่างลดลงความสัมพันธ์ของสัญญาณจะสูงขึ้น
เดลต้าโมดูเลเตอร์
Delta Modulator ประกอบด้วย quantizer 1 บิตและวงจรหน่วงเวลาพร้อมกับวงจรฤดูร้อนสองวงจร ต่อไปนี้เป็นแผนภาพบล็อกของโมดูเลเตอร์เดลต้า
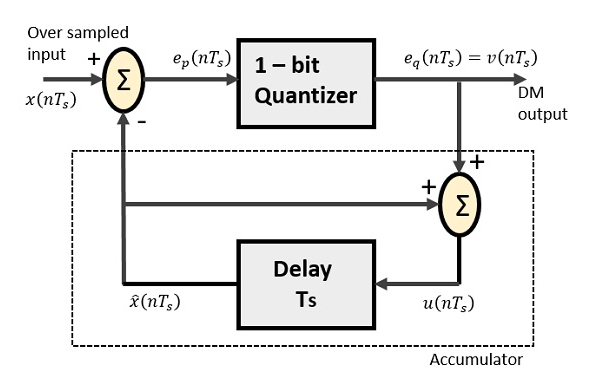
วงจรทำนายใน DPCM ถูกแทนที่ด้วยวงจรหน่วงเวลาแบบธรรมดาใน DM
จากแผนภาพด้านบนเรามีสัญกรณ์ดังนี้ -
$ x (nT_ {s}) $ = มากกว่าอินพุตตัวอย่าง
$ e_ {p} (nT_ {s}) $ = เอาต์พุตในช่วงฤดูร้อนและอินพุตปริมาณ
$ e_ {q} (nT_ {s}) $ = quantizer output = $ v (nT_s) $
$ \ widehat {x} (nT_ {s}) $ = เอาต์พุตของวงจรหน่วงเวลา
$ u (nT_ {s}) $ = อินพุตของวงจรหน่วงเวลา
เมื่อใช้สัญกรณ์เหล่านี้ตอนนี้เราจะพยายามหาขั้นตอนการมอดูเลตเดลต้า
$ e_ {p} (nT_ {s}) = x (nT_ {s}) - \ widehat {x} (nT_ {s}) $
--------- สมการ 1
$ = x (nT_ {s}) - u ([n - 1] T_ {s}) $
$ = x (nT_ {s}) - [\ widehat {x} [[n - 1] T_ {s}] + v [[n-1] T_ {s}]] $
--------- สมการ 2
นอกจากนี้
$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig. [e_ {p} (nT_ {s})] $
--------- สมการ 3
$ u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s}) $
ที่ไหน
$ \ widehat {x} (nT_ {s}) $ = ค่าก่อนหน้าของวงจรหน่วงเวลา
$ e_ {q} (nT_ {s}) $ = quantizer output = $ v (nT_s) $
ดังนั้น
$ u (nT_ {s}) = u ([n-1] T_ {s}) + v (nT_ {s}) $
--------- สมการ 4
ซึ่งหมายความว่า,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
สมมติว่าเงื่อนไขเป็นศูนย์ของการสะสม
$ u (nT_ {s}) = S \ displaystyle \ sum \ LIMIT_ {j = 1} ^ n sig [e_ {p} (jT_ {s})] $
Accumulated version of DM output = $ \ displaystyle \ sum \ LIMIT_ {j = 1} ^ nv (jT_ {s}) $
--------- สมการ 5
ตอนนี้โปรดทราบว่า
$ \ widehat {x} (nT_ {s}) = u ([n-1] T_ {s}) $
$ = \ displaystyle \ sum \ LIMIT_ {j = 1} ^ {n - 1} v (jT_ {s}) $
--------- สมการ 6
เอาท์พุทของหน่วยหน่วงเวลาคือเอาต์พุต Accumulator ที่ปกคลุมด้วยวัตถุฉนวนหนึ่งตัวอย่าง
จากสมการ 5 และ 6 เราได้โครงสร้างที่เป็นไปได้สำหรับเดโมดูเลเตอร์
รูปคลื่นโดยประมาณของ Stair-case จะเป็นเอาต์พุตของเดลต้าโมดูเลเตอร์ที่มีขนาดขั้นตอนเป็นเดลต้า (Δ). คุณภาพเอาต์พุตของรูปคลื่นอยู่ในระดับปานกลาง
Delta Demodulator
เดโมดูเลเตอร์เดลต้าประกอบด้วยตัวกรองความถี่ต่ำฤดูร้อนและวงจรหน่วงเวลา วงจรทำนายจะถูกตัดออกที่นี่และด้วยเหตุนี้จึงไม่มีการป้อนข้อมูลที่สันนิษฐานให้กับเครื่องถอดรหัส
ต่อไปนี้เป็นแผนภาพสำหรับเดโมดูเลเตอร์เดลต้า
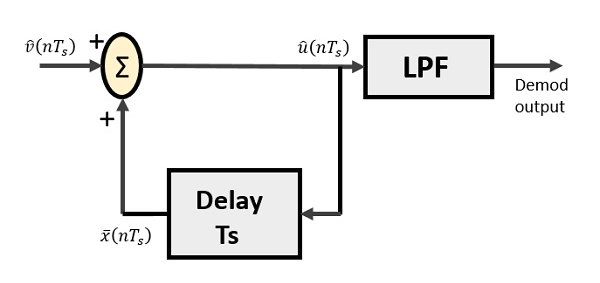
จากแผนภาพด้านบนเรามีสัญกรณ์ดังนี้ -
$ \ widehat {v} (nT_ {s}) $ คือตัวอย่างอินพุต
$ \ widehat {u} (nT_ {s}) $ คือผลผลิตในช่วงฤดูร้อน
$ \ bar {x} (nT_ {s}) $ คือเอาต์พุตล่าช้า
ลำดับไบนารีจะถูกกำหนดให้เป็นอินพุตสำหรับเดโมดูเลเตอร์ เอาต์พุตโดยประมาณของบันไดกรณีถูกกำหนดให้กับ LPF
ตัวกรองความถี่ต่ำถูกนำมาใช้ด้วยเหตุผลหลายประการ แต่เหตุผลที่สำคัญคือการกำจัดสัญญาณรบกวนสำหรับสัญญาณนอกย่านความถี่ ข้อผิดพลาดขนาดขั้นตอนที่อาจเกิดขึ้นที่เครื่องส่งสัญญาณเรียกว่าgranular noiseซึ่งถูกกำจัดที่นี่ หากไม่มีสัญญาณรบกวนเอาต์พุตของโมดูเลเตอร์จะเท่ากับอินพุตเดโมดูเลเตอร์
ข้อดีของ DM มากกว่า DPCM
Quantizer 1 บิต
การออกแบบโมดูเลเตอร์และเดโมดูเลเตอร์ที่ง่ายมาก
อย่างไรก็ตามมีเสียงรบกวนใน DM
ความลาดชันเกินความผิดเพี้ยนของโหลด (เมื่อ Δ เล็ก)
เสียงรบกวน (เมื่อ Δ มีขนาดใหญ่)
Adaptive Delta Modulation (ADM)
ในการมอดูเลตแบบดิจิทัลเราพบปัญหาบางอย่างในการกำหนดขนาดขั้นตอนซึ่งมีผลต่อคุณภาพของคลื่นสัญญาณขาออก
จำเป็นต้องมีขนาดขั้นบันไดที่ใหญ่ขึ้นในความลาดชันของสัญญาณมอดูเลตและจำเป็นต้องมีขนาดขั้นบันไดที่เล็กลงซึ่งข้อความมีความลาดเอียงเล็กน้อย รายละเอียดนาทีพลาดในกระบวนการ ดังนั้นจะดีกว่าถ้าเราสามารถควบคุมการปรับขนาดขั้นตอนตามความต้องการของเราเพื่อให้ได้มาซึ่งการสุ่มตัวอย่างตามแบบที่ต้องการ นี่คือแนวคิดของAdaptive Delta Modulation.
ต่อไปนี้เป็นแผนภาพบล็อกของ Adaptive delta modulator
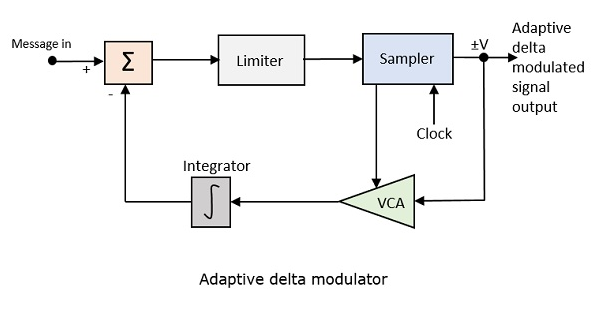
อัตราขยายของแอมพลิฟายเออร์ที่ควบคุมแรงดันไฟฟ้าจะถูกปรับโดยสัญญาณเอาต์พุตจากตัวอย่าง อัตราขยายของเครื่องขยายเสียงกำหนดขนาดของขั้นตอนและทั้งสองอย่างเป็นสัดส่วน
ADM จะวัดความแตกต่างระหว่างมูลค่าของตัวอย่างปัจจุบันและค่าที่คาดการณ์ไว้ของตัวอย่างถัดไป ใช้ความสูงของขั้นตอนที่แปรผันเพื่อทำนายค่าถัดไปสำหรับการสร้างค่าที่แตกต่างกันอย่างรวดเร็วอย่างซื่อสัตย์