การสื่อสารดิจิทัล - การสุ่มตัวอย่าง
Sampling หมายถึง“ กระบวนการวัดค่าทันทีของสัญญาณเวลาต่อเนื่องในรูปแบบไม่ต่อเนื่อง”
Sample เป็นข้อมูลที่นำมาจากข้อมูลทั้งหมดซึ่งต่อเนื่องกันในโดเมนเวลา
เมื่อแหล่งที่มาสร้างสัญญาณแอนะล็อกและหากต้องแปลงเป็นดิจิทัลให้มี 1s และ 0sกล่าวคือสูงหรือต่ำสัญญาณจะต้องถูกแยกออกในเวลา การแยกสัญญาณแอนะล็อกนี้เรียกว่าการสุ่มตัวอย่าง
รูปต่อไปนี้แสดงสัญญาณเวลาต่อเนื่อง x (t) และสัญญาณตัวอย่าง xs (t). เมื่อไหร่x (t) คูณด้วยรถไฟอิมพัลส์เป็นระยะซึ่งเป็นสัญญาณตัวอย่าง xs (t) ได้รับ
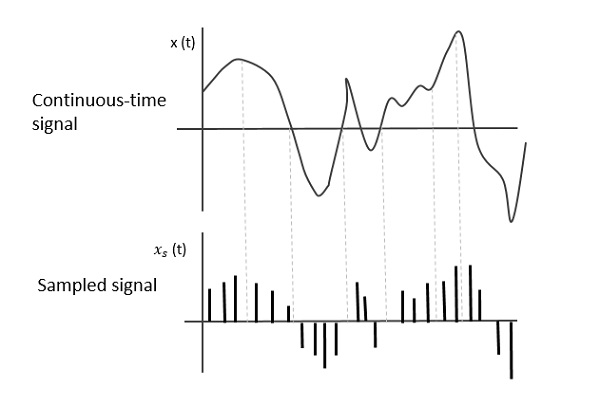
อัตราการสุ่มตัวอย่าง
ในการแยกแยะสัญญาณควรแก้ไขช่องว่างระหว่างตัวอย่าง ช่องว่างนั้นสามารถเรียกได้ว่าเป็นไฟล์sampling period Ts.
$$ การสุ่มตัวอย่าง \: ความถี่ = \ frac {1} {T_ {s}} = f_s $$ที่ไหน
$ T_ {s} $ คือเวลาสุ่มตัวอย่าง
$ f_ {s} $ คือความถี่ในการสุ่มตัวอย่างหรืออัตราการสุ่มตัวอย่าง
Sampling frequencyคือผลต่างของช่วงเวลาการสุ่มตัวอย่าง ความถี่ในการสุ่มตัวอย่างนี้สามารถเรียกง่ายๆว่าSampling rate. อัตราการสุ่มตัวอย่างหมายถึงจำนวนตัวอย่างที่ได้รับต่อวินาทีหรือสำหรับชุดค่าที่ จำกัด
สำหรับสัญญาณแอนะล็อกที่จะสร้างขึ้นใหม่จากสัญญาณดิจิทัลควรพิจารณาอัตราการสุ่มตัวอย่างเป็นอย่างมาก อัตราของการสุ่มตัวอย่างควรเป็นเช่นที่ข้อมูลในสัญญาณข้อความไม่ควรสูญหายและไม่ควรถูกทับ ดังนั้นอัตราจึงคงที่สำหรับสิ่งนี้เรียกว่าอัตรานิควิสต์
อัตรา Nyquist
สมมติว่าสัญญาณถูก จำกัด วงโดยไม่มีส่วนประกอบความถี่สูงกว่า Wเฮิรตซ์. นั่นหมายความว่า,Wคือความถี่สูงสุด สำหรับสัญญาณดังกล่าวเพื่อให้ได้สัญญาณต้นฉบับที่มีประสิทธิภาพอัตราการสุ่มตัวอย่างควรเป็นสองเท่าของความถี่สูงสุด
ซึ่งหมายความว่า,
$$ f_ {S} = 2W $$ที่ไหน
$ f_ {S} $ คืออัตราการสุ่มตัวอย่าง
W คือความถี่สูงสุด
อัตราการสุ่มตัวอย่างนี้เรียกว่า Nyquist rate.
ทฤษฎีบทที่เรียกว่า Sampling Theorem ถูกระบุไว้ในทฤษฎีของอัตรานิควิสต์นี้
ทฤษฎีบทการสุ่มตัวอย่าง
ทฤษฎีบทการสุ่มตัวอย่างซึ่งเรียกอีกอย่างว่า Nyquist theoremนำเสนอทฤษฎีอัตราตัวอย่างที่เพียงพอในแง่ของแบนด์วิดท์สำหรับคลาสของฟังก์ชันที่ จำกัด แบนด์วิดท์
ทฤษฎีบทการสุ่มตัวอย่างระบุว่า“ สัญญาณสามารถทำซ้ำได้อย่างแน่นอนหากมีการสุ่มตัวอย่างในอัตรา fs ซึ่งมากกว่าสองเท่าของความถี่สูงสุด W.”
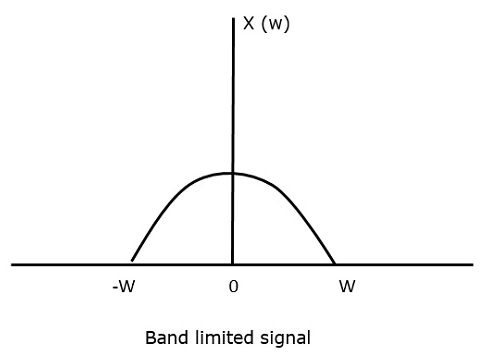
เพื่อทำความเข้าใจกับทฤษฎีบทการสุ่มตัวอย่างนี้ให้เราพิจารณาสัญญาณ จำกัด วงนั่นคือสัญญาณที่มีค่า non-zero ระหว่างบางคน –W และ W เฮิรตซ์.
สัญญาณดังกล่าวแสดงเป็น $x(f) = 0 for |f\lvert > W$
สำหรับสัญญาณเวลาต่อเนื่อง x (t)สัญญาณ จำกัด แบนด์ในโดเมนความถี่สามารถแสดงได้ดังแสดงในรูปต่อไปนี้
เราต้องการความถี่ในการสุ่มตัวอย่างซึ่งเป็นความถี่ที่ข้อมูลไม่ควรสูญหายแม้หลังจากการสุ่มตัวอย่างแล้วก็ตาม สำหรับสิ่งนี้เรามีอัตรา Nyquist ที่ความถี่ในการสุ่มตัวอย่างควรเป็นสองเท่าของความถี่สูงสุด เป็นอัตราวิกฤตของการสุ่มตัวอย่าง
ถ้าสัญญาณ x(t) มีการสุ่มตัวอย่างสูงกว่าอัตรา Nyquist สัญญาณดั้งเดิมสามารถกู้คืนได้และหากสุ่มตัวอย่างต่ำกว่าอัตรา Nyquist สัญญาณจะไม่สามารถกู้คืนได้
รูปต่อไปนี้อธิบายสัญญาณหากสุ่มตัวอย่างด้วยอัตราที่สูงกว่า 2w ในโดเมนความถี่
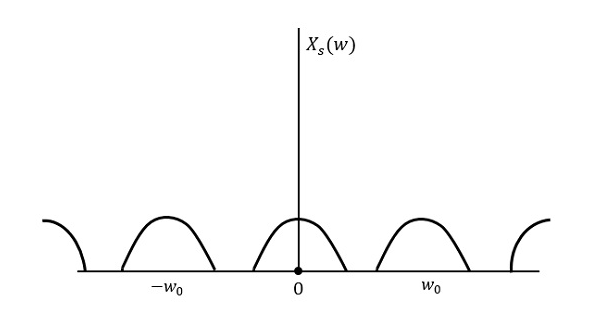
รูปด้านบนแสดงการแปลงฟูริเยร์ของสัญญาณ $x_{s}(t)$. ที่นี่ข้อมูลจะถูกทำซ้ำโดยไม่มีการสูญเสียใด ๆ ไม่มีการปะปนและด้วยเหตุนี้การกู้คืนจึงเป็นไปได้
การแปลงฟูเรียร์ของสัญญาณ $x_{s}(t)$ คือ
$$ X_ {s} (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0) $$โดยที่ $ T_ {s} $ = Sampling Period และ $ w_ {0} = \ frac {2 \ pi} {T_s} $
ให้เราดูว่าจะเกิดอะไรขึ้นถ้าอัตราการสุ่มตัวอย่างเท่ากับสองเท่าของความถี่สูงสุด (2W)
นั่นหมายความว่า,
$$ f_ {s} = 2W $$ที่ไหน
$ f_ {s} $ คือความถี่ในการสุ่มตัวอย่าง
W คือความถี่สูงสุด
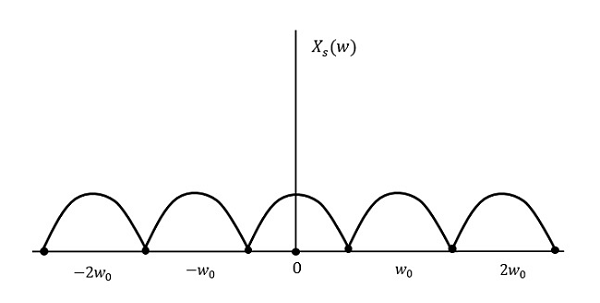
ผลลัพธ์จะเป็นดังที่แสดงในรูปด้านบน ข้อมูลจะถูกแทนที่โดยไม่มีการสูญเสียใด ๆ ดังนั้นนี่จึงเป็นอัตราการสุ่มตัวอย่างที่ดีเช่นกัน
ตอนนี้ให้เราดูสภาพ
$$ f_ {s} <2W $$รูปแบบผลลัพธ์จะมีลักษณะดังรูปต่อไปนี้

เราสามารถสังเกตได้จากรูปแบบข้างต้นว่ามีการทำข้อมูลมากเกินไปซึ่งนำไปสู่การปะปนและการสูญเสียข้อมูล ปรากฏการณ์ที่ไม่ต้องการของการทับซ้อนนี้เรียกว่านามแฝง
นามแฝง
การใช้นามแฝงสามารถเรียกได้ว่าเป็น“ ปรากฏการณ์ของส่วนประกอบความถี่สูงในสเปกตรัมของสัญญาณโดยคำนึงถึงตัวตนของส่วนประกอบความถี่ต่ำในสเปกตรัมของเวอร์ชันตัวอย่าง”
มาตรการแก้ไขเพื่อลดผลกระทบของนามแฝงคือ -
ในส่วนเครื่องส่งของ PCM ก low pass anti-aliasing filter ใช้ก่อนเครื่องเก็บตัวอย่างเพื่อกำจัดส่วนประกอบความถี่สูงซึ่งไม่ต้องการ
สัญญาณที่สุ่มตัวอย่างหลังจากการกรองจะถูกสุ่มตัวอย่างในอัตราที่สูงกว่าอัตรา Nyquist เล็กน้อย
การเลือกอัตราการสุ่มตัวอย่างสูงกว่าอัตรา Nyquist นี้ยังช่วยในการออกแบบไฟล์ reconstruction filter ที่เครื่องรับ
ขอบเขตของการแปลงฟูเรียร์
เป็นที่สังเกตโดยทั่วไปว่าเราขอความช่วยเหลือจากอนุกรมฟูริเยร์และการแปลงฟูริเยร์ในการวิเคราะห์สัญญาณและในการพิสูจน์ทฤษฎีบท เป็นเพราะ -
การแปลงฟูริเยร์เป็นส่วนขยายของอนุกรมฟูริเยร์สำหรับสัญญาณที่ไม่ใช่คาบ
การแปลงฟูเรียร์เป็นเครื่องมือทางคณิตศาสตร์ที่มีประสิทธิภาพซึ่งช่วยในการดูสัญญาณในโดเมนต่างๆและช่วยในการวิเคราะห์สัญญาณได้อย่างง่ายดาย
สัญญาณใด ๆ สามารถย่อยสลายได้ในรูปของผลรวมของไซน์และโคไซน์โดยใช้การแปลงฟูริเยร์นี้
ในบทถัดไปให้เราพูดคุยเกี่ยวกับแนวคิดของ Quantization