ทฤษฎีบทการเข้ารหัสแหล่งที่มา
รหัสที่ผลิตโดยแหล่งหน่วยความจำแบบไม่ต่อเนื่องจะต้องแสดงอย่างมีประสิทธิภาพซึ่งเป็นปัญหาสำคัญในการสื่อสาร เพื่อให้สิ่งนี้เกิดขึ้นมีคำรหัสซึ่งแสดงถึงรหัสที่มาเหล่านี้
ตัวอย่างเช่นในการโทรเลขเราใช้รหัสมอร์สซึ่งตัวอักษรจะแสดงด้วย Marks และ Spaces. ถ้าตัวอักษรE ได้รับการพิจารณาซึ่งส่วนใหญ่จะใช้แสดงโดย “.” ในขณะที่จดหมาย Q ซึ่งไม่ค่อยได้ใช้แสดงโดย “--.-”
ให้เราดูที่แผนภาพบล็อก
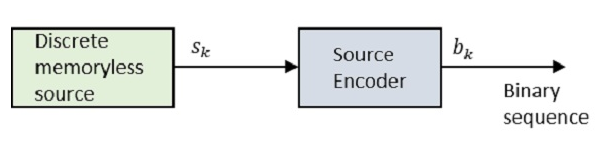
ที่ไหน Sk คือเอาต์พุตของแหล่งที่มาของหน่วยความจำแบบไม่ต่อเนื่องและ bk คือเอาต์พุตของตัวเข้ารหัสต้นทางซึ่งแสดงโดย 0s และ 1s.
ลำดับที่เข้ารหัสนั้นจะถูกถอดรหัสอย่างสะดวกที่เครื่องรับ
ให้เราสมมติว่าแหล่งที่มามีตัวอักษรด้วย k สัญลักษณ์ที่แตกต่างกันและ kth สัญลักษณ์ Sk เกิดขึ้นกับความน่าจะเป็น Pk, ที่ไหน k = 0, 1…k-1.
ให้คำรหัสไบนารีกำหนดให้กับสัญลักษณ์ Skโดยตัวเข้ารหัสมีความยาว lkวัดเป็นบิต
ดังนั้นเราจึงกำหนดความยาวคำรหัสเฉลี่ยLของตัวเข้ารหัสต้นทางเป็น
$$ \ overline {L} = \ displaystyle \ sum \ LIMIT_ {k = 0} ^ {k-1} p_kl_k $$
L แสดงจำนวนบิตเฉลี่ยต่อสัญลักษณ์ต้นทาง
ถ้า $ L_ {min} = \: Minimum \: possible \: value \: of \: \ overline {L} $
แล้ว coding efficiency สามารถกำหนดเป็น
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
ด้วย $ \ overline {L} \ geq L_ {min} $ เราจะมี $ \ eta \ leq 1 $
อย่างไรก็ตามตัวเข้ารหัสต้นทางถือว่ามีประสิทธิภาพเมื่อ $ \ eta = 1 $
สำหรับสิ่งนี้จะต้องกำหนดค่า $ L_ {min} $
ให้เราอ้างถึงคำจำกัดความที่ว่า"ให้แหล่งที่มาของเอนโทรปีแบบไม่ต่อเนื่องหน่วยความจำ $ H (\ delta) $ ความยาวรหัส - คำเฉลี่ยL สำหรับการเข้ารหัสแหล่งที่มาใด ๆ จะมีขอบเขตเป็น $ \ overline {L} \ geq H (\ delta) $ "
ในคำที่ง่ายกว่านั้นคำรหัส (ตัวอย่าง: รหัสมอร์สสำหรับคำว่า QUEUE คือ -.- ..-. ..-.) จะมากกว่าหรือเท่ากับซอร์สโค้ดเสมอ (ตัวอย่างเช่น QUEUE) ซึ่งหมายความว่าสัญลักษณ์ในคำรหัสมีค่ามากกว่าหรือเท่ากับตัวอักษรในซอร์สโค้ด
ดังนั้นด้วย $ L_ {min} = H (\ delta) $ ประสิทธิภาพของตัวเข้ารหัสต้นทางในแง่ของเอนโทรปี $ H (\ delta) $ อาจเขียนเป็น
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$
ทฤษฎีบทการเข้ารหัสแหล่งที่มานี้เรียกว่า as noiseless coding theoremเนื่องจากสร้างการเข้ารหัสที่ปราศจากข้อผิดพลาด จะเรียกอีกอย่างว่าShannon’s first theorem.