Plotly - Box Plot Violin Plot and Contour Plot
บทนี้มุ่งเน้นไปที่ความเข้าใจในรายละเอียดเกี่ยวกับพล็อตต่างๆรวมถึงพล็อตบ็อกซ์พล็อตไวโอลินโครงร่างและพล็อตสั่น ในขั้นต้นเราจะเริ่มต้นด้วย Box Plot ตาม
พล็อตกล่อง
พล็อตกล่องแสดงข้อมูลสรุปชุดข้อมูลที่มีค่าต่ำสุด first quartile, median, third quartileและ maximum. ในพล็อตกล่องเราวาดกล่องจากควอร์ไทล์แรกไปยังควอร์ไทล์ที่สาม เส้นแนวตั้งผ่านกล่องที่ค่ามัธยฐาน เส้นที่ยื่นออกมาในแนวตั้งจากกล่องที่แสดงความแปรปรวนนอกควอไทล์บนและล่างเรียกว่าหนวด ดังนั้นพล็อตกล่องจึงเรียกอีกอย่างว่ากล่องและwhisker plot. หนวดจะเปลี่ยนจากแต่ละควอไทล์เป็นค่าต่ำสุดหรือสูงสุด
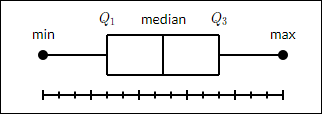
ในการวาดแผนภูมิกล่องเราต้องใช้ go.Box()ฟังก์ชัน ชุดข้อมูลสามารถกำหนดให้กับพารามิเตอร์ x หรือ y ดังนั้นพล็อตกล่องจะถูกวาดในแนวนอนหรือแนวตั้ง ในตัวอย่างต่อไปนี้ยอดขายของ บริษัท บางแห่งในสาขาต่างๆจะถูกแปลงเป็นกล่องแนวนอน แสดงค่ามัธยฐานของค่าต่ำสุดและสูงสุด
trace1 = go.Box(y = [1140,1460,489,594,502,508,370,200])
data = [trace1]
fig = go.Figure(data)
iplot(fig)ผลลัพธ์ที่เหมือนกันจะเป็นดังนี้ -
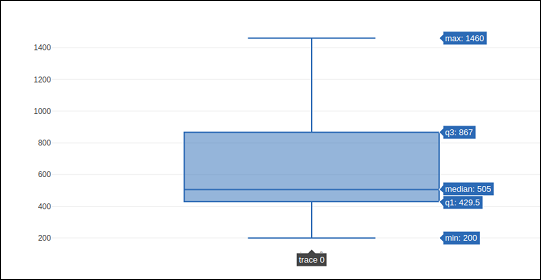
go.Box()ฟังก์ชันสามารถกำหนดพารามิเตอร์อื่น ๆ เพื่อควบคุมลักษณะและพฤติกรรมของพล็อตกล่อง หนึ่งในนั้นคือพารามิเตอร์ boxmean
boxmeanพารามิเตอร์ถูกตั้งค่าเป็นจริงตามค่าเริ่มต้น ด้วยเหตุนี้ค่าเฉลี่ยของการแจกแจงพื้นฐานของกล่องจึงถูกวาดเป็นเส้นประภายในกล่อง หากตั้งค่าเป็น sd ค่าเบี่ยงเบนมาตรฐานของการแจกแจงจะถูกดึงออกมาด้วย
boxpoints พารามิเตอร์เป็นค่าเริ่มต้นเท่ากับ "outliers". จะแสดงเฉพาะจุดตัวอย่างที่อยู่นอกหนวดเท่านั้นหาก" สงสัยว่าคู่ค้า "จะมีการแสดงจุดผิดปกติและชี้น้อยกว่า 4" Q1-3 "Q3 หรือมากกว่า 4" Q3-3 "Q1 จะถูกไฮไลต์ถ้า" False "จะแสดงเฉพาะช่องที่ไม่มีจุดตัวอย่าง
ในตัวอย่างต่อไปนี้ไฟล์ box trace วาดด้วยค่าเบี่ยงเบนมาตรฐานและจุดผิดปกติ
trc = go.Box(
y = [
0.75, 5.25, 5.5, 6, 6.2, 6.6, 6.80, 7.0, 7.2, 7.5, 7.5, 7.75, 8.15,
8.15, 8.65, 8.93, 9.2, 9.5, 10, 10.25, 11.5, 12, 16, 20.90, 22.3, 23.25
],
boxpoints = 'suspectedoutliers', boxmean = 'sd'
)
data = [trc]
fig = go.Figure(data)
iplot(fig)ผลลัพธ์เดียวกันระบุไว้ด้านล่าง -

พล็อตไวโอลิน
แปลงไวโอลินคล้ายกับแปลงกล่องยกเว้นว่าจะแสดงความหนาแน่นของข้อมูลที่ค่าต่างกันด้วย แปลงไวโอลินจะมีเครื่องหมายสำหรับค่ามัธยฐานของข้อมูลและกล่องที่ระบุช่วงระหว่างควอไทล์เช่นเดียวกับพล็อตกล่องมาตรฐาน การวางซ้อนบนพล็อตกล่องนี้เป็นการประมาณความหนาแน่นของเคอร์เนล เช่นเดียวกับพล็อตบ็อกซ์พล็อตไวโอลินถูกใช้เพื่อแสดงการเปรียบเทียบการกระจายตัวแปร (หรือการแจกแจงตัวอย่าง) ใน "ประเภท" ต่างๆ
พล็อตไวโอลินให้ข้อมูลมากกว่าพล็อตกล่องธรรมดา ในความเป็นจริงในขณะที่พล็อตบ็อกซ์จะแสดงเฉพาะสถิติสรุปเช่นค่าเฉลี่ย / ค่ามัธยฐานและช่วงระหว่างควอไทล์full distribution of the data.
วัตถุติดตามไวโอลินถูกส่งคืนโดย go.Violin() ฟังก์ชันใน graph_objectsโมดูล. ในการแสดงพล็อตกล่องที่อยู่ภายใต้ไฟล์boxplot_visibleแอตทริบิวต์ถูกตั้งค่าเป็น True ในทำนองเดียวกันโดยการตั้งค่าmeanline_visible คุณสมบัติเป็นจริงเส้นที่ตรงกับค่าเฉลี่ยของตัวอย่างจะแสดงอยู่ภายในไวโอลิน
ตัวอย่างต่อไปนี้แสดงให้เห็นถึงวิธีการแสดงพล็อตไวโอลินโดยใช้ฟังก์ชันการทำงานของ plotly
import numpy as np
np.random.seed(10)
c1 = np.random.normal(100, 10, 200)
c2 = np.random.normal(80, 30, 200)
trace1 = go.Violin(y = c1, meanline_visible = True)
trace2 = go.Violin(y = c2, box_visible = True)
data = [trace1, trace2]
fig = go.Figure(data = data)
iplot(fig)ผลลัพธ์มีดังนี้ -

โครงร่างโครงร่าง
พล็อตรูปร่าง 2 มิติแสดงเส้นชั้นความสูงของอาร์เรย์ตัวเลข 2 มิติ z นั่นคือเส้นที่สอดแทรกของ isovaluesของ z. เส้นชั้นความสูงของฟังก์ชันของตัวแปรสองตัวคือเส้นโค้งที่ฟังก์ชันมีค่าคงที่เพื่อให้เส้นโค้งรวมจุดที่มีค่าเท่ากัน
โครงร่างมีความเหมาะสมหากคุณต้องการดูว่าค่า Z บางค่าเปลี่ยนไปอย่างไรเมื่อเป็นฟังก์ชันของสองอินพุต X และ Y ดังนั้น Z = f(X,Y). เส้นชั้นความสูงหรือไอโซลีนของฟังก์ชันของตัวแปรสองตัวคือเส้นโค้งที่ฟังก์ชันมีค่าคงที่
ตัวแปรอิสระ x และ y มักถูก จำกัด ไว้ที่ตารางปกติที่เรียกว่า meshgrid numpy.meshgrid สร้างตารางสี่เหลี่ยมจากอาร์เรย์ของค่า x และอาร์เรย์ของค่า y
ก่อนอื่นให้เราสร้างค่าข้อมูลสำหรับ x, y และ z โดยใช้ linspace()ฟังก์ชันจากไลบรารี Numpy เราสร้างไฟล์meshgrid จากค่า x และ y และรับอาร์เรย์ z ที่ประกอบด้วยรากที่สองของ x2+y2
เรามี go.Contour() ฟังก์ชันใน graph_objects โมดูลที่ใช้ xy และ zคุณลักษณะ. ข้อมูลโค้ดต่อไปนี้แสดงโครงร่างของ xy และ z ค่าที่คำนวณตามด้านบน
import numpy as np
xlist = np.linspace(-3.0, 3.0, 100)
ylist = np.linspace(-3.0, 3.0, 100)
X, Y = np.meshgrid(xlist, ylist)
Z = np.sqrt(X**2 + Y**2)
trace = go.Contour(x = xlist, y = ylist, z = Z)
data = [trace]
fig = go.Figure(data)
iplot(fig)ผลลัพธ์มีดังนี้ -

โครงร่างโครงร่างสามารถปรับแต่งได้ด้วยพารามิเตอร์ต่อไปนี้อย่างน้อยหนึ่งพารามิเตอร์ -
Transpose (boolean) - เปลี่ยนข้อมูล z
ถ้า xtype (หรือ ytype) เท่ากับ "อาร์เรย์" พิกัด x / y กำหนดโดย "x" / "y" ถ้า "มาตราส่วน" พิกัด x จะถูกกำหนดโดย "x0" และ "dx".
connectgaps พารามิเตอร์กำหนดว่าจะเติมช่องว่างในข้อมูล z หรือไม่
ค่าเริ่มต้นของ ncontoursพารามิเตอร์คือ 15 จำนวนรูปทรงจริงจะถูกเลือกโดยอัตโนมัติให้น้อยกว่าหรือเท่ากับค่าของ "ncontours" จะมีผลเฉพาะในกรณีที่ "autocontour" เป็น "True"
ประเภทรูปทรงเป็นค่าเริ่มต้น: "levelsดังนั้นข้อมูลจะแสดงเป็นโครงร่างที่มีการแสดงหลายระดับถ้า constrainข้อมูลจะแสดงเป็นข้อ จำกัด โดยมีการแรเงาภูมิภาคที่ไม่ถูกต้องตามที่ระบุโดย operation และ value พารามิเตอร์
showlines - กำหนดว่าจะวาดเส้นชั้นความสูงหรือไม่
zauto คือ True ตามค่าเริ่มต้นและกำหนดว่าโดเมนสีถูกคำนวณโดยคำนึงถึงข้อมูลอินพุตหรือไม่ (ที่นี่ใน "z`) หรือขอบเขตที่กำหนดใน"zmin`และ"zmax`ค่าเริ่มต้นเป็น"False"เมื่อผู้ใช้ตั้งค่า" zmin "และ" zmax "
พล็อตสั่น
พล็อตสั่นเป็นที่รู้จักกันในชื่อ velocity plot. จะแสดงเวกเตอร์ความเร็วเป็นลูกศรพร้อมส่วนประกอบ (u,v) ที่จุด (x, y) ในการวาดพล็อต Quiver เราจะใช้create_quiver() ฟังก์ชันที่กำหนดใน figure_factory โมดูลใน Plotly
Python API ของ Plotly มีโมดูลโรงงานร่างซึ่งรวมถึงฟังก์ชัน wrapper จำนวนมากที่สร้างประเภทแผนภูมิเฉพาะที่ยังไม่รวมอยู่ใน plotly.jsไลบรารีกราฟโอเพนซอร์สของ Plotly
ฟังก์ชัน create_quiver () ยอมรับพารามิเตอร์ต่อไปนี้ -
x - พิกัด x ของตำแหน่งลูกศร
y - พิกัด y ของตำแหน่งลูกศร
u - ส่วนประกอบ x ของเวกเตอร์ลูกศร
v - ส่วนประกอบ y ของเวกเตอร์ลูกศร
scale - ขนาดขนาดของลูกศร
arrow_scale - ความยาวของหัวลูกศร
angle - มุมของหัวลูกศร
โค้ดต่อไปนี้แสดงพล็อตสั่นอย่างง่ายในสมุดบันทึก Jupyter -
import plotly.figure_factory as ff
import numpy as np
x,y = np.meshgrid(np.arange(-2, 2, .2), np.arange(-2, 2, .25))
z = x*np.exp(-x**2 - y**2)
v, u = np.gradient(z, .2, .2)
# Create quiver figure
fig = ff.create_quiver(x, y, u, v,
scale = .25, arrow_scale = .4,
name = 'quiver', line = dict(width = 1))
iplot(fig)ผลลัพธ์ของรหัสมีดังนี้ -
