Makine Öğrenimi - Beceriler
Makine Öğreniminin çok geniş bir genişliği vardır ve birçok alanda beceri gerektirir. Makine Öğrenimi konusunda uzman olmak için edinmeniz gereken beceriler aşağıda listelenmiştir -
- Statistics
- Olasılık Teorileri
- Calculus
- Optimizasyon teknikleri
- Visualization
Çeşitli Makine Öğrenimi Becerilerinin Gerekliliği
Hangi becerileri edinmeniz gerektiğine dair size kısa bir fikir vermek için, bazı örnekleri tartışalım -
Matematiksel Gösterim
Makine öğrenimi algoritmalarının çoğu ağırlıklı olarak matematiğe dayalıdır. Bilmeniz gereken matematik seviyesi muhtemelen başlangıç seviyesidir. Önemli olan, matematikçilerin denklemlerinde kullandıkları notasyonu okuyabilmenizdir. Örneğin, notasyonu okuyabilir ve bunun ne anlama geldiğini kavrayabilirseniz, makine öğrenimini öğrenmeye hazırsınız demektir. Değilse, matematik bilginizi tazelemeniz gerekebilir.
$$ f_ {AN} (net- \ theta) = \ begin {case} \ gamma & if \: net- \ theta \ geq \ epsilon \\ net- \ theta & if - \ epsilon <net- \ theta <\ epsilon \\ - \ gamma & if \: net- \ theta \ leq- \ epsilon \ end {case} $$
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m etiket ^ \ left (\ begin {dizi} {c} i \\ \ end {dizi} \ sağ) \ cdot \: label ^ \ left (\ begin {dizi} {c} j \\ \ end {dizi} \ sağ) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {dizi} {c} i \\ \ end {dizi} \ sağ), x ^ \ left (\ begin {dizi} {c} j \\ \ end {dizi} \ sağ) \ rangle \ end {bmatrix} $$
$$ f_ {AN} (net- \ theta) = \ left (\ frac {e ^ {\ lambda (net- \ theta)} - e ^ {- \ lambda (net- \ theta)}} {e ^ { \ lambda (net- \ theta)} + e ^ {- \ lambda (net- \ theta)}} \ sağ) \; $$
Olasılık teorisi
İşte olasılık teorisi hakkındaki mevcut bilginizi test etmek için bir örnek: Koşullu olasılıklarla sınıflandırma.
$$ p (c_ {i} | x, y) \; = \ frac {p (x, y | c_ {i}) \; p (c_ {i}) \;} {p (x, y) \ ;} $$
Bu tanımlarla Bayes sınıflandırma kuralını tanımlayabiliriz -
- P (c1 | x, y)> P (c2 | x, y) ise, sınıf c1'dir.
- P (c1 | x, y) <P (c2 | x, y) ise, sınıf c2'dir.
Optimizasyon Sorunu
İşte bir optimizasyon işlevi
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m etiket ^ \ left (\ begin {dizi} {c} i \\ \ end {dizi} \ sağ) \ cdot \: label ^ \ left (\ begin {dizi} {c} j \\ \ end {dizi} \ sağ) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {dizi} {c} i \\ \ end {dizi} \ sağ), x ^ \ left (\ begin {dizi} {c} j \\ \ end {dizi} \ sağ) \ rangle \ end {bmatrix} $$
Aşağıdaki kısıtlamalara tabi -
$$ \ alpha \ geq0 ve \: \ displaystyle \ sum \ limits_ {i-1} ^ m \ alpha_ {i} \ cdot \: etiket ^ \ left (\ begin {dizi} {c} i \\ \ end {dizi} \ sağ) = 0 $$
Yukarıdakileri okuyabilir ve anlayabilirseniz, hazırsınız demektir.
Görselleştirme
Çoğu durumda, veri dağıtımınızı anlamak ve algoritmanın çıktısının sonuçlarını yorumlamak için çeşitli görselleştirme grafiklerini anlamanız gerekecektir.
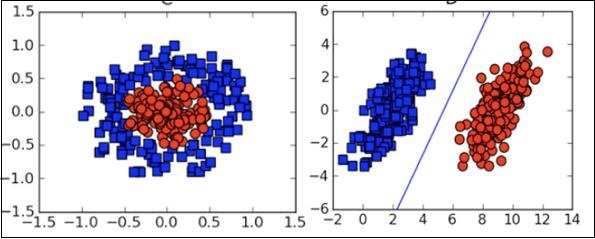
Makine öğreniminin yukarıdaki teorik yönlerinin yanı sıra, bu algoritmaları kodlamak için iyi programlama becerilerine ihtiyacınız var.
Peki ML'yi uygulamak için ne gerekiyor? Bir sonraki bölümde buna bakalım.