Regresyon Teknikleri
Regresyon, birbiriyle ilişkili ekonomik değişkenler arasındaki ilişkiyi nitelendirmeye yardımcı olan istatistiksel bir tekniktir. İlk adım, bağımsız değişkenin katsayısını tahmin etmeyi ve ardından tahmin edilen katsayının güvenilirliğini ölçmeyi içerir. Bu, bir hipotez formüle etmeyi gerektirir ve hipoteze dayanarak bir işlev oluşturabiliriz.
Bir yönetici firmanın reklam harcamaları ile satış geliri arasındaki ilişkiyi belirlemek isterse, hipotez testinden geçecektir. Daha yüksek reklam harcamalarının bir firma için daha yüksek satışa yol açtığını varsayarsak. Yönetici, belirli bir zaman diliminde reklam harcamaları ve satış gelirleri hakkında veri toplar. Bu hipotez matematiksel fonksiyona çevrilebilir, burada -
Y = A + Bx
Nerede Y satış, x reklam harcaması, A ve B sabittir.
Hipotezi işleve dönüştürdükten sonra, bunun temeli bağımlı ve bağımsız değişkenler arasındaki ilişkiyi bulmaktır. Bağımlı değişkenin değeri, araştırmacılar için çok önemlidir ve diğer değişkenlerin değerine bağlıdır. Bağımlı değişkendeki değişimi açıklamak için bağımsız değişken kullanılır. İki türe ayrılabilir -
Simple regression - Bir bağımsız değişken
Multiple regression - Birkaç bağımsız değişken
Basit Regresyon
Aşağıda, regresyon analizi oluşturma adımları verilmiştir -
- Regresyon modelini belirtin
- Değişkenler hakkında veri elde edin
- Nicel ilişkileri tahmin edin
- Sonuçların istatistiksel önemini test edin
- Karar vermede sonuçların kullanılması
Basit regresyon için formül -
Y = a + bX + u
Y= bağımlı değişken
X= bağımsız değişken
a= engelleme
b= eğim
u= rastgele faktör
Kesitsel veriler, belirli bir zamanda bir varlık grubu hakkında bilgi sağlarken, zaman serisi verileri zaman içinde bir varlık hakkında bilgi sağlar. Regresyon denklemini tahmin ettiğimizde, bağımlı ve bağımsız değişkenler arasındaki en iyi doğrusal ilişkiyi bulma sürecini içerir.
Sıradan En Küçük Kareler Yöntemi (OLS)
Sıradan en küçük kareler yöntemi, noktaların dağılması yoluyla bir çizgiye uyacak şekilde tasarlanmıştır, öyle ki, noktaların çizgiden sapmalarının karesi toplamı en aza indirilir. İstatistiksel bir yöntemdir. Genellikle Yazılım paketleri OLS tahminini gerçekleştirir.
Y = a + bX
Belirlemenin Ortak Etkinliği (R 2 )
Belirlemenin ortak verimliliği, bağımlı değişkendeki varyasyon yüzdesinin bağımsız değişkenlerdeki varyasyonlardan kaynaklandığını gösteren bir ölçüdür. R, 2 uygun modelin iyilik bir ölçüsüdür. Yöntemler aşağıdadır -
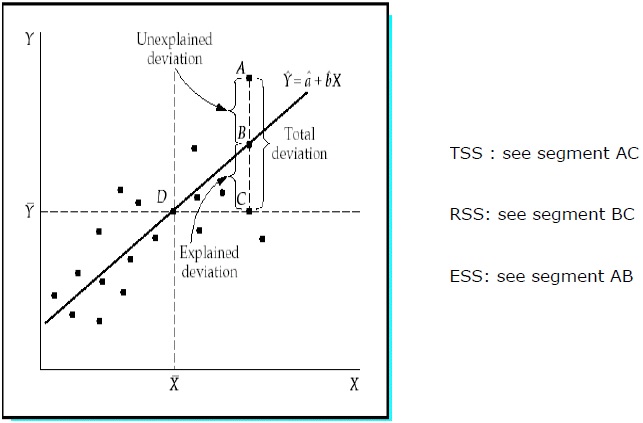
Toplam Kareler Toplamı (TSS)
Y'nin örnek değerlerinin Y ortalamasından kare sapmalarının toplamı.
TSS = SUM ( Yi − Y)2
Yi = bağımlı değişkenler
Y = bağımlı değişkenlerin ortalaması
i = gözlem sayısı
Regresyon Kareler Toplamı (RSS)
Y'nin tahmini değerlerinin Y ortalamasından kare sapmalarının toplamı.
RSS = SUM ( Ỷi − uY)2
Ỷi = Y'nin tahmini değeri
Y = bağımlı değişkenlerin ortalaması
i = varyasyon sayısı
Hata Kareler Toplamı (ESS)
Y'nin örnek değerlerinin Y'nin tahmini değerlerinden kare sapmalarının toplamı.
ESS = SUM ( Yi − Ỷi)2
Ỷi = Y'nin tahmini değeri
Yi = bağımlı değişkenler
i = gözlem sayısı
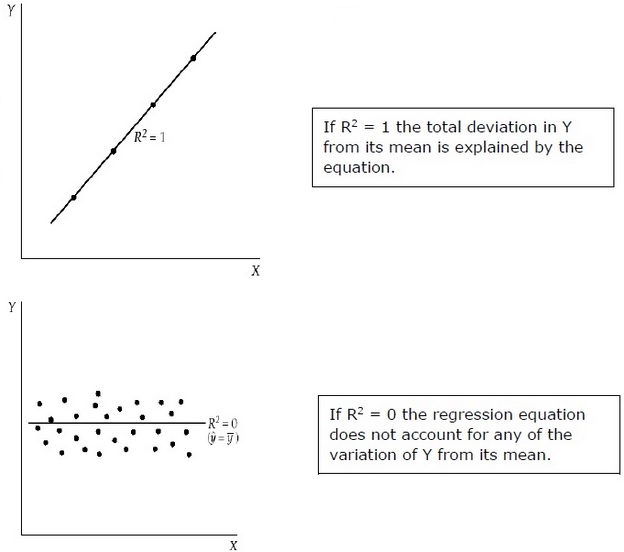
R, 2 ölçer regresyon modeli ile açıklanmaktadır kendi ortalamasından Y toplam sapma oranı. Yakın R ' 2 daha büyük, birlik regresyon denklemi açıklayıcı güçtür. Bir R 2 0'a yakın regresyon denklemi çok az açıklayıcı bir güce sahip olduğunu göstermektedir.
Regresyon katsayılarını değerlendirmek için, tüm popülasyon yerine popülasyondan bir örneklem kullanılır. Örneğe dayalı olarak nüfus hakkında varsayımlar yapmak ve bu varsayımların ne kadar iyi olduğuna dair bir yargıya varmak önemlidir.
Regresyon Katsayılarının Değerlendirilmesi
Popülasyondaki her örnek kendi kesişimini oluşturur. İstatistiksel farkı hesaplamak için aşağıdaki yöntemler kullanılabilir -
Two tailed test −
Boş Hipotez: H 0 : b = 0
Alternatif Hipotez: H a : b ≠ 0
One tailed test −
Boş Hipotez: H 0 : b> 0 (veya b <0)
Alternatif Hipotez: H a : b <0 (veya b> 0)
Statistic Test −
b = tahmini katsayı
E (b) = b = 0 (Boş hipotez)
SE b = Katsayının standart hatası
.Değeri tserbestlik derecesine, bir veya iki başarısız teste ve anlamlılık düzeyine bağlıdır. Kritik değerini belirlemek içint, t-table kullanılabilir. Ardından t-değerinin kritik değerle karşılaştırılması gelir. İstatistik testinin mutlak değeri kritik t-değerinden büyük veya ona eşitse boş hipotezin reddedilmesi gerekir. Sıfır hipotezini reddetmeyin, I istatistik testinin mutlak değeri kritik t değerinden düşüktür.
Çoklu Regresyon Analizi
Çoklu regresyon analizindeki basit regresyondan farklı olarak, katsayılar, diğer değişkenlerin değerlerinin sabit olduğunu varsayarak bağımlı değişkenlerdeki değişimi gösterir.
İstatistiksel anlamlılık testi denir F-test. F testi, sadece bir birey için değil, tüm regresyon denkleminin istatistiksel önemini ölçtüğü için kullanışlıdır. Burada sıfır hipotezinde bağımlı değişken ile popülasyonun bağımsız değişkenleri arasında bir ilişki yoktur.
Formül - H 0 : b1 = b2 = b3 =… şeklindedir. = bk = 0
Bağımlı değişken ile k popülasyon için bağımsız değişkenler.
F-test static −
$$ F \: = \: \ frac {\ left (\ frac {R ^ 2} {K} \ right)} {\ frac {(1-R ^ 2)} {(nk-1)}} $$
Kritik değeri Fpay ve payda serbestlik derecesi ve anlamlılık düzeyine bağlıdır. Kritik F değerini belirlemek için F tablosu kullanılabilir. Kritik değere (F *) sahip F değeri ile karşılaştırıldığında -
F> F * ise, sıfır hipotezini reddetmemiz gerekir.
F <F * ise, bağımlı değişken ile tüm bağımsız değişkenler arasında anlamlı bir ilişki olmadığı için boş hipotezi reddetmeyin.