Bir tablo yapmak ve birim oran verilen noktaları işaretlemek
Unit rate paydanın 1 olduğu bir oran olarak tanımlanır. Genel olarak, birim oran, bir bağımsız değişken başına bağımlı değişkenlerin sayısıdır.
For example - Bir maymun 2 dakikada 8 muz yer
Buradaki birim oran, maymunun bir dakika içinde yediği muz sayısıdır.
Birim oranı = 8/2 = dakikada 4 muz.
Unit rate and table
Örneğin orantılı bir ilişkimiz varsa $9 for 3 kg, we can make a table of values and graph the relationship. We already have learnt about unit rate. In this case the unit rate is the number of dollars per 1 kg. Here the unit rate is found as $9 / 3kg = 3 $ / kg.
Orantılı ilişkileri temsil eden bir tablo veya grafikte, orantılılık sabiti ve birim oran aynıdır.
Bir birim oran verildiğinde, aşağıdaki orantılı ilişkiyi izleyerek x ve y değer çiftleri yazabiliriz. Örneğin birim fiyat 3 $ / kg ise yazabiliriz (1kg,$3), (2 kg, $6), (3 kg, $9), (4 kg, $12), (5 kg, 15 $) vb. Sonra bu sıralı çiftleri aşağıdaki gibi bir tabloya koyarız.
| Ağırlık kg (x) | $ (Y) cinsinden maliyet |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| 5 | 15 |
Unit rate and graph
Verilen oran için orantılı ilişki $ 3 / kg y = 3x denklemi olarak yazılabilir. Aynısı, aşağıda verilen bir grafik olarak çizilebilir.
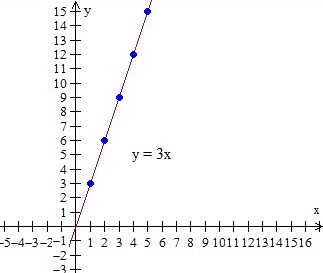
Bir birim oran verildiğinde, y = mx gibi bir fonksiyon kuralı yazabiliriz, burada m birim oran, x ve y değişkenlerdir. Bu kuralı kullanarak bir tabloya konulabilecek x ve y değerlerine sahip noktalar bulabiliriz. Sonra bu noktaları bir grafik üzerine çizeriz.
Birim orana sahip ilişki aşağıdaki denklemde verilmiştir: y = 2x + 1 Bir tablo yapın ve 5 noktayı işaretleyin.
Çözüm
Step 1:
Y = 2x + 1 denkleminde,
X = 0, y = 1, x = 1, y = 3 ve benzeri için
Farklı x değerleri için aşağıdaki tabloyu alıyoruz
| Giriş (x) | Çıktı (y) |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
Step 2:
Bu noktaları çizerek bu grafiği elde ederiz

Birim orana sahip ilişki aşağıdaki denklemle verilir: y = 5x. Bir tablo yapın ve 5 noktayı işaretleyin.
Çözüm
Step 1:
Y = 5x denkleminde
X = 0, y = 0, x = 1, y = 5 vb. İçin
Farklı x değerleri için aşağıdaki tabloyu alıyoruz
| Giriş (x) | Çıktı (y) |
|---|---|
| 0 | 0 |
| 1 | 5 |
| 2 | 10 |
| 3 | 15 |
| 4 | 20 |
Step 2:
Bu noktaları çizerek bu grafiği elde ederiz
