Đại số Boolean

Boolean Algebra được sử dụng để phân tích và đơn giản hóa các mạch số (logic). Nó chỉ sử dụng các số nhị phân tức là 0 và 1. Nó còn được gọi làBinary Algebra hoặc là logical Algebra. Đại số Boolean được phát minh bởiGeorge Boole vào năm 1854.

Quy tắc trong Đại số Boolean

Sau đây là các quy tắc quan trọng được sử dụng trong đại số Boolean.

• Biến được sử dụng chỉ có thể có hai giá trị. Nhị phân 1 cho CAO và Nhị phân 0 cho THẤP.

• Phần bổ sung của một biến được biểu thị bằng dấu gạch ngang (-). Do đó, phần bù của biến B được biểu diễn dưới dạng

  
  . Do đó nếu B = 0 thì
  
  = 1 và B = 1 thì
  
  = 0.

• ORing của các biến được biểu diễn bằng dấu cộng (+) giữa chúng. Ví dụ ORing của A, B, C được biểu diễn là A + B + C.

• Hợp lý ANDing của hai hoặc nhiều biến được biểu diễn bằng cách viết một dấu chấm giữa chúng, chẳng hạn như ABC Đôi khi dấu chấm có thể bị bỏ qua như ABC.

Luật Boolean

Có sáu loại Luật Boolean.

Luật thay thế

Bất kỳ phép toán nhị phân nào thỏa mãn biểu thức sau được gọi là phép toán giao hoán.

Luật giao hoán phát biểu rằng việc thay đổi trình tự của các biến không có bất kỳ ảnh hưởng nào đến đầu ra của mạch logic.

Luật kết hợp

Luật này tuyên bố rằng thứ tự thực hiện các phép toán logic là không liên quan vì tác dụng của chúng là như nhau.

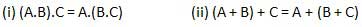
Luật phân phối

Luật phân phối phát biểu điều kiện sau.

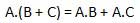
Luật VÀ

Các luật này sử dụng phép toán AND. Do đó chúng được gọi làAND luật.

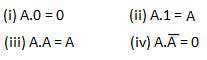
HOẶC luật

Các luật này sử dụng phép toán OR. Do đó chúng được gọi làOR luật.

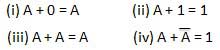
Luật ĐẦU TƯ

Luật này sử dụng phép toán NOT. Luật nghịch đảo phát biểu rằng đảo đôi một biến dẫn đến chính biến ban đầu.

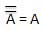
Định lý Boolean quan trọng

Sau đây là một vài Định lý boolean quan trọng.

Hàm / định lý Boolean	Sự miêu tả
Các hàm Boolean	Các hàm và biểu thức Boolean, bản đồ K-Map và hiện thực hóa Cổng NAND
Định lý De Morgan	Định lý De Morgan 1 và Định lý 2