Mạch kết hợp

Mạch kết hợp là mạch trong đó chúng ta kết hợp các cổng khác nhau trong mạch, ví dụ bộ mã hóa, bộ giải mã, bộ ghép kênh và bộ phân kênh. Một số đặc điểm của mạch tổ hợp là:

Đầu ra của mạch tổ hợp tại bất kỳ thời điểm nào, chỉ phụ thuộc vào các mức hiện diện tại các thiết bị đầu cuối đầu vào.
Mạch tổ hợp không sử dụng bất kỳ bộ nhớ nào. Trạng thái trước đó của đầu vào không có bất kỳ ảnh hưởng nào đến trạng thái hiện tại của mạch.
Một mạch tổ hợp có thể có n số đầu vào và m số đầu ra.

Sơ đồ khối

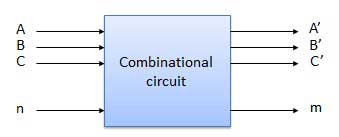
Chúng ta sẽ giải thích một số mạch tổ hợp quan trọng như sau.

Một nửa Adder

Bộ cộng nửa là một mạch logic tổ hợp với hai đầu vào và hai đầu ra. Mạch cộng một nửa được thiết kế để thêm hai số nhị phân bit đơn A và B. Nó là khối xây dựng cơ bản để cộng haisinglesố bit. Mạch này có hai đầu racarry và sum.

Sơ đồ khối

Bảng sự thật

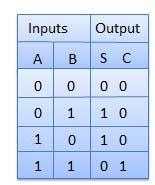
Sơ đồ mạch

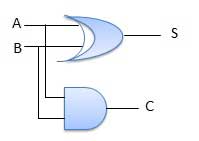
Adder đầy đủ

Bộ cộng đầy đủ được phát triển để khắc phục nhược điểm của mạch Half Adder. Nó có thể thêm hai số một bit A và B, và mang c. Bộ cộng đầy đủ là một mạch tổ hợp ba đầu vào và hai đầu ra.

Sơ đồ khối

Bảng sự thật

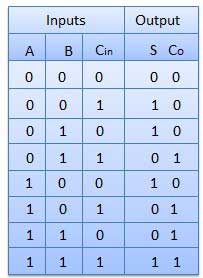
Sơ đồ mạch

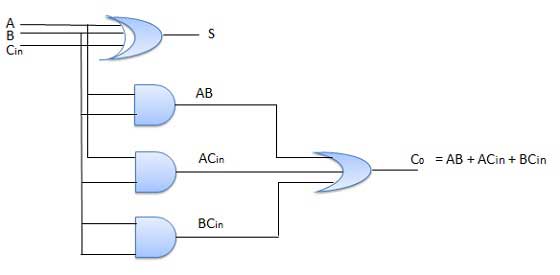
Trình quảng cáo song song N-Bit

Full Adder chỉ có thể thêm hai số nhị phân một chữ số cùng với một đầu vào mang. Nhưng trong thực tế, chúng ta cần thêm các số nhị phân dài hơn nhiều so với chỉ một bit. Để thêm hai số nhị phân n-bit, chúng ta cần sử dụng bộ cộng song song n-bit. Nó sử dụng một số bộ cộng đầy đủ theo tầng. Đầu ra mang của bộ cộng đầy đủ trước đó được kết nối với đầu vào mang của bộ cộng đầy đủ tiếp theo.

Trình quảng cáo song song 4 bit

Trong sơ đồ khối, A ₀ và B ₀ đại diện cho LSB của bốn từ bit A và B. Do đó Full Adder-0 là giai đoạn thấp nhất. Do đó C _trong của nó đã được tạo vĩnh viễn bằng 0. Phần còn lại của các kết nối giống hệt như kết nối của bộ cộng song song n-bit được chỉ ra trong hình. Bộ cộng song song bốn bit là một mạch logic rất phổ biến.

Sơ đồ khối

Dấu trừ song song N-Bit

Phép trừ có thể được thực hiện bằng cách lấy phần bù 1 hoặc 2 của số bị trừ. Ví dụ, chúng ta có thể thực hiện phép trừ (AB) bằng cách thêm phần bù 1 hoặc 2 của B vào A. Điều đó có nghĩa là chúng ta có thể sử dụng bộ cộng nhị phân để thực hiện phép trừ nhị phân.

Dấu trừ song song 4 bit

Số bị trừ (B) trước tiên được chuyển qua các bộ nghịch lưu để lấy phần bù 1 của nó. Sau đó, bộ cộng 4 bit sẽ thêm phần bù của A và 2 của B để tạo ra phép trừ. S ₃ S ₂ S ₁ S ₀ đại diện cho kết quả của phép trừ nhị phân (AB) và thực hiện đầu ra C _ra đại diện cho cực của kết quả. Nếu A> B thì Cout = 0 và kết quả ở dạng nhị phân (AB) thì C _out = 1 và kết quả ở dạng bù 2.

Sơ đồ khối

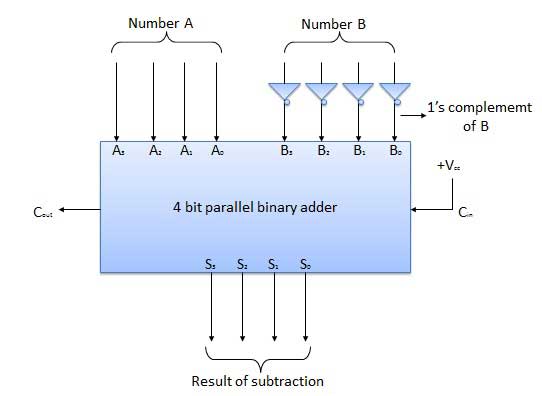
Dấu trừ một nửa

Bộ trừ một nửa là một mạch kết hợp với hai đầu vào và hai đầu ra (chênh lệch và mượn). Nó tạo ra sự khác biệt giữa hai bit nhị phân ở đầu vào và cũng tạo ra đầu ra (Mượn) để cho biết liệu 1 đã được mượn hay chưa. Trong phép trừ (AB), A được gọi là bit Minuend và B được gọi là bit Subtrahend.

Bảng sự thật

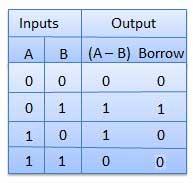
Sơ đồ mạch

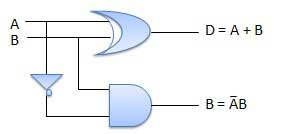
Dấu trừ đầy đủ

Nhược điểm của bộ trừ một nửa được khắc phục bằng bộ trừ đầy đủ. Bộ trừ đầy đủ là một mạch tổ hợp với ba đầu vào A, B, C và hai đầu ra D và C '. A là 'minuend', B là 'subtrahend', C là 'vay' do giai đoạn trước tạo ra, D là sản lượng chênh lệch và C 'là sản lượng đi vay.

Bảng sự thật

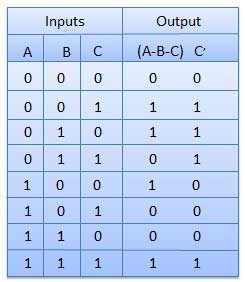
Sơ đồ mạch

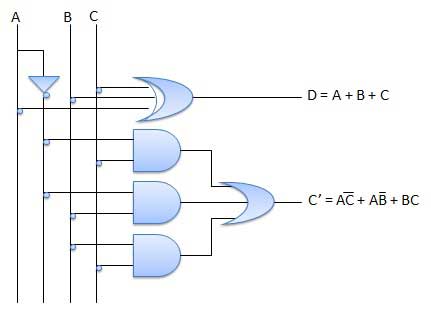
Bộ ghép kênh

Bộ ghép kênh là một loại mạch tổ hợp đặc biệt. Có n đầu vào dữ liệu, một đầu ra và m đầu vào chọn với 2m = n. Nó là một mạch kỹ thuật số chọn một trong n đầu vào dữ liệu và định tuyến nó đến đầu ra. Việc lựa chọn một trong n đầu vào được thực hiện bởi các đầu vào đã chọn. Tùy thuộc vào mã kỹ thuật số được áp dụng tại các đầu vào đã chọn, một trong số n nguồn dữ liệu được chọn và truyền đến đầu ra duy nhất Y. E được gọi là đầu vào nhấp nháy hoặc kích hoạt hữu ích cho việc phân tầng. Nó thường là một thiết bị đầu cuối đang hoạt động có nghĩa là nó sẽ thực hiện hoạt động cần thiết khi nó ở mức thấp.

Sơ đồ khối

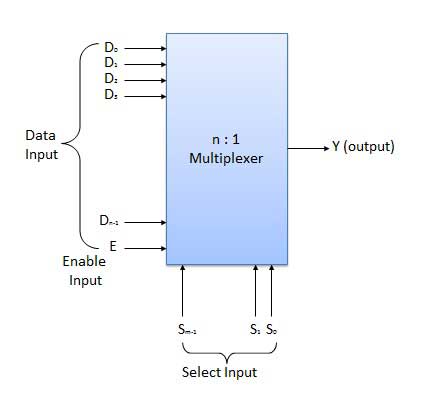
Bộ ghép kênh có nhiều biến thể

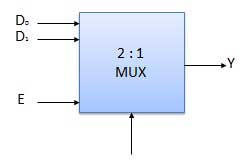
Bộ ghép kênh 2: 1
Bộ ghép kênh 4: 1
Bộ ghép kênh 16: 1
Bộ ghép kênh 32: 1

Sơ đồ khối

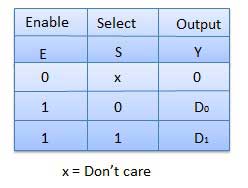
Bảng sự thật

Bộ phân kênh

Một bộ phân kênh thực hiện hoạt động ngược lại của một bộ ghép kênh tức là nó nhận một đầu vào và phân phối nó trên một số đầu ra. Nó chỉ có một đầu vào, n đầu ra, m đầu vào chọn. Tại một thời điểm chỉ có một dòng đầu ra được chọn bởi các dòng được chọn và đầu vào được truyền đến dòng đầu ra đã chọn. Một bộ khử ghép kênh tương đương với một bộ chuyển mạch đa chiều một cực như trong hình.

Bộ tách kênh có nhiều biến thể.

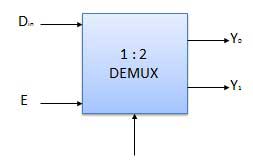
Bộ tách kênh 1: 2
Bộ tách kênh 1: 4
Bộ phân kênh 1: 16
Bộ tách kênh 1: 32

Sơ đồ khối

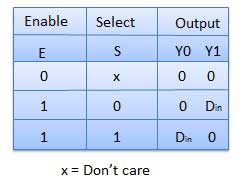
Bảng sự thật

Người giải mã

Bộ giải mã là một mạch tổ hợp. Nó có n đầu vào và tối đa m = 2n đầu ra. Bộ giải mã giống hệt như một bộ phân kênh mà không cần bất kỳ đầu vào dữ liệu nào. Nó thực hiện các hoạt động hoàn toàn ngược lại với các hoạt động của một bộ mã hóa.

Sơ đồ khối

Sau đây là các ví dụ về Bộ giải mã.

Bộ chuyển đổi mã
BCD đến bộ giải mã bảy đoạn
Bộ giải mã ống Nixie
Bộ truyền động rơ le

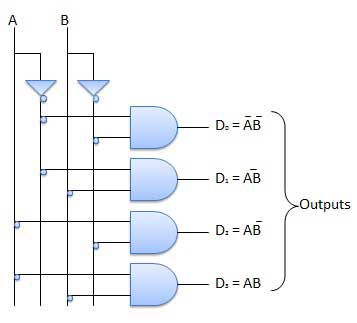
Bộ giải mã 2 đến 4 dòng

Sơ đồ khối của bộ giải mã 2 đến 4 dòng được hiển thị trong hình. A và B là hai đầu vào trong đó D đến D là bốn đầu ra. Bảng chân lý giải thích các hoạt động của bộ giải mã. Nó chỉ ra rằng mỗi đầu ra là 1 chỉ cho một sự kết hợp cụ thể của các đầu vào.

Sơ đồ khối

Bảng sự thật

Mạch logic

Mã hoá

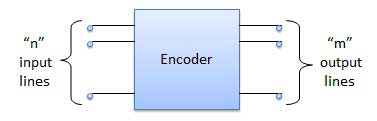
Bộ mã hóa là một mạch tổ hợp được thiết kế để thực hiện hoạt động nghịch đảo của bộ giải mã. Một bộ mã hóa có n số dòng đầu vào và m số dòng đầu ra. Một bộ mã hóa tạo ra một mã nhị phân m bit tương ứng với số đầu vào kỹ thuật số. Bộ mã hóa chấp nhận một từ kỹ thuật số đầu vào n và chuyển đổi nó thành một từ kỹ thuật số khác m bit.

Sơ đồ khối

Sau đây là các ví dụ về Bộ mã hóa.

Bộ mã hóa ưu tiên
Bộ mã hóa thập phân sang BCD
Bộ mã hóa bát phân sang nhị phân
Bộ mã hóa thập lục phân sang nhị phân

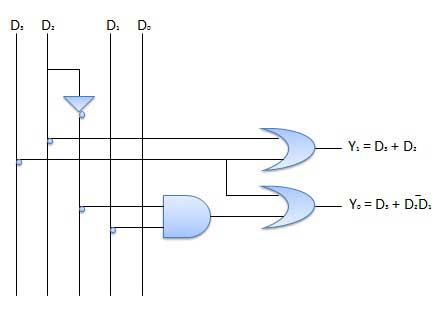
Bộ mã hóa ưu tiên

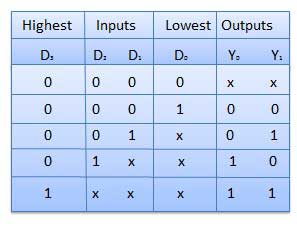
Đây là một loại bộ mã hóa đặc biệt. Ưu tiên các dòng đầu vào. Nếu hai hoặc nhiều dòng đầu vào là 1 cùng một lúc, thì dòng đầu vào có mức độ ưu tiên cao nhất sẽ được xem xét. Có bốn đầu vào D ₀ , D ₁ , D ₂ , D ₃ và hai đầu ra Y ₀ , Y ₁ . Trong số bốn đầu vào, D ₃ có mức ưu tiên cao nhất và D ₀ có mức ưu tiên thấp nhất. Điều đó có nghĩa là nếu D ₃ = 1 thì Y ₁ Y ₁ = 11 bất kể các đầu vào khác. Tương tự nếu D ₃ = 0 và D ₂ = 1 thì Y ₁ Y ₀ = 10 không phụ thuộc vào các đầu vào khác.