Hướng dẫn nhanh
Trong thế giới điện tử hiện đại, thuật ngữ Digital thường được kết hợp với máy tính vì thuật ngữ Digitalcó nguồn gốc từ cách máy tính thực hiện hoạt động, bằng cách đếm các chữ số. Trong nhiều năm, ứng dụng của điện tử kỹ thuật số chỉ là trong hệ thống máy tính. Nhưng ngày nay, điện tử kỹ thuật số được sử dụng trong nhiều ứng dụng khác. Sau đây là một số ví dụ trong đóDigital electronics được sử dụng nhiều.
- Kiểm soát quy trình công nghiệp
- Hệ thống quân sự
- Television
- Hệ thống thông tin liên lạc
- Trang thiết bị y tế
- Radar
- Navigation
Tín hiệu
Signalcó thể được định nghĩa như một đại lượng vật lý, chứa một số thông tin. Nó là một hàm của một hoặc nhiều hơn một biến độc lập. Tín hiệu có hai loại.
- Tín hiệu tương tự
- Tín hiệu kĩ thuật số
Tín hiệu tương tự
An analog signalđược định nghĩa là tín hiệu có giá trị liên tục. Tín hiệu tương tự có thể có vô số giá trị khác nhau. Trong kịch bản thế giới thực, hầu hết những thứ được quan sát trong tự nhiên là tương tự. Dưới đây là các ví dụ về tín hiệu tương tự.
- Temperature
- Pressure
- Distance
- Sound
- Voltage
- Current
- Power
Biểu diễn đồ họa của tín hiệu tương tự (Nhiệt độ)
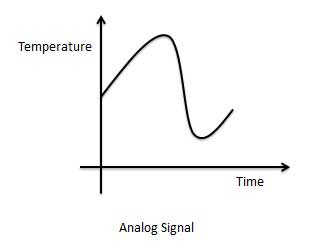
Các mạch xử lý tín hiệu tương tự được gọi là mạch tương tự hoặc hệ thống. Sau đây là các ví dụ về hệ thống tương tự.
- Filter
- Amplifiers
- Máy thu hình
- Bộ điều khiển tốc độ động cơ
Nhược điểm của Hệ thống Analog
- Độ chính xác kém hơn
- Ít tính linh hoạt
- Thêm hiệu ứng tiếng ồn
- Méo mó hơn
- Thêm ảnh hưởng của thời tiết
Tín hiệu kĩ thuật số
A digital signalđược định nghĩa là tín hiệu chỉ có một số hữu hạn các giá trị khác biệt. Tín hiệu số không phải là tín hiệu liên tục. Trong máy tính điện tử kỹ thuật số, đầu vào được đưa ra với sự trợ giúp của công tắc. Đầu vào này được chuyển đổi thành tín hiệu điện có hai giá trị hoặc mức riêng biệt. Một trong số này có thể được gọi là mức thấp và một mức khác được gọi là mức cao. Tín hiệu sẽ luôn là một trong hai mức. Loại tín hiệu này được gọi là tín hiệu số. Dưới đây là các ví dụ về tín hiệu kỹ thuật số.
- Tín hiệu nhị phân
- Tín hiệu bát phân
- Tín hiệu thập lục phân
Biểu diễn đồ họa của tín hiệu kỹ thuật số (nhị phân)
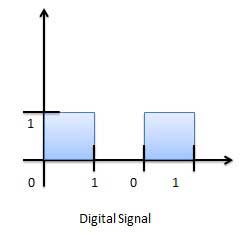
Các mạch xử lý tín hiệu số được gọi là hệ thống số hoặc mạch số. Dưới đây là ví dụ về các hệ thống kỹ thuật số.
- Registers
- Flip-flop
- Counters
- Microprocessors
Lợi thế của hệ thống kỹ thuật số
- Chính xác hơn
- Tính linh hoạt hơn
- Ít biến dạng
- Giao tiếp dễ dàng
- Có thể lưu trữ thông tin
So sánh tín hiệu tương tự và tín hiệu kỹ thuật số
| SN | Tín hiệu tương tự | Tín hiệu kĩ thuật số |
|---|---|---|
| 1 | Tín hiệu tương tự có giá trị vô hạn. | Tín hiệu số có một số giá trị hữu hạn. |
| 2 | Tín hiệu tương tự có tính chất liên tục. | Tín hiệu số có tính chất rời rạc. |
| 3 | Tín hiệu tương tự được tạo ra bởi bộ chuyển đổi và bộ tạo tín hiệu. | Tín hiệu kỹ thuật số được tạo ra bởi bộ chuyển đổi A sang D. |
| 4 | Ví dụ về tín hiệu tương tự - sóng sin, sóng tam giác. | Ví dụ về tín hiệu số - tín hiệu nhị phân. |
Một hệ thống kỹ thuật số chỉ có thể hiểu hệ thống số vị trí khi có một vài ký hiệu được gọi là chữ số và những ký hiệu này đại diện cho các giá trị khác nhau tùy thuộc vào vị trí mà chúng chiếm trong số.
Giá trị của mỗi chữ số trong một số có thể được xác định bằng cách sử dụng
Chữ số
Vị trí của chữ số trong số
Cơ số của hệ thống số (trong đó cơ số được định nghĩa là tổng số chữ số có sẵn trong hệ thống số).
Hệ thống số thập phân
Hệ thống số mà chúng ta sử dụng trong cuộc sống hàng ngày là hệ thống số thập phân. Hệ thống số thập phân có cơ số 10 vì nó sử dụng 10 chữ số từ 0 đến 9. Trong hệ thống số thập phân, các vị trí liên tiếp ở bên trái của dấu thập phân biểu thị đơn vị, hàng chục, hàng trăm, hàng nghìn, v.v.
Mỗi vị trí thể hiện một sức mạnh cụ thể của căn cứ (10). Ví dụ: số thập phân 1234 bao gồm chữ số 4 ở vị trí hàng đơn vị, 3 ở vị trí hàng chục, 2 ở vị trí hàng trăm và 1 ở vị trí hàng nghìn, và giá trị của nó có thể được viết dưới dạng
(1×1000) + (2×100) + (3×10) + (4×l)
(1×103) + (2×102) + (3×101) + (4×l00)
1000 + 200 + 30 + 1
1234Là một lập trình viên máy tính hoặc một chuyên gia CNTT, bạn nên hiểu các hệ thống số sau đây thường được sử dụng trong máy tính.
| SN | Hệ thống Số & Mô tả |
|---|---|
| 1 | Binary Number System Cơ sở 2. Các chữ số được sử dụng: 0, 1 |
| 2 | Octal Number System Cơ số 8. Các chữ số được sử dụng: 0 đến 7 |
| 3 | Hexa Decimal Number System Cơ số 16. Chữ số được sử dụng: 0 đến 9, Các chữ cái được sử dụng: A- F |
Hệ thống số nhị phân
Nét đặc trưng
Sử dụng hai chữ số, 0 và 1.
Còn được gọi là hệ cơ số 2
Mỗi vị trí trong một số nhị phân đại diện cho một lũy thừa 0 của cơ số (2). Ví dụ: 2 0
Vị trí cuối cùng trong một số nhị phân thể hiện lũy thừa x của cơ số (2). Ví dụ: 2 x trong đó x đại diện cho vị trí cuối cùng - 1.
Thí dụ
Số nhị phân: 10101 2
Tính tương đương thập phân -
| Bươc | Số nhị phân | Số thập phân |
|---|---|---|
| Bước 1 | 10101 2 | ((1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| Bước 2 | 10101 2 | (16 + 0 + 4 + 0 + 1) 10 |
| Bước 3 | 10101 2 | 21 10 |
Note:10101 2 thường được viết là 10101.
Hệ thống số bát phân
Nét đặc trưng
Sử dụng tám chữ số 0,1,2,3,4,5,6,7.
Còn được gọi là hệ cơ số 8
Mỗi vị trí trong một số bát phân đại diện cho một lũy thừa 0 của cơ số (8). Ví dụ: 8 0
Vị trí cuối cùng trong một số bát phân thể hiện lũy thừa x của cơ số (8). Ví dụ: 8 x trong đó x đại diện cho vị trí cuối cùng - 1.
Thí dụ
Số bát phân - 12570 8
Tính tương đương thập phân -
| Bươc | Số bát phân | Số thập phân |
|---|---|---|
| Bước 1 | 12570 8 | ((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10 |
| Bước 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| Bước 3 | 12570 8 | 5496 10 |
Note:12570 8 thường được viết là 12570.
Hệ thống số thập lục phân
Nét đặc trưng
Sử dụng 10 chữ số và 6 chữ cái, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
Các chữ cái đại diện cho các số bắt đầu từ 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Còn được gọi là hệ cơ số 16.
Mỗi vị trí trong một số thập lục phân đại diện cho một lũy thừa 0 của cơ số (16). Ví dụ 16 0 .
Vị trí cuối cùng trong một số thập lục phân thể hiện lũy thừa x của cơ số (16). Ví dụ 16 x trong đó x đại diện cho vị trí cuối cùng - 1.
Ví dụ -
Số thập lục phân: 19FDE 16
Tính tương đương thập phân -
| Bươc | Số thập lục phân | Số thập phân |
|---|---|---|
| Bước 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Bước 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| Bước 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| Bước 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 thường được viết là 19FDE.
Có nhiều phương pháp hoặc kỹ thuật có thể được sử dụng để chuyển đổi số từ cơ số này sang cơ số khác. Chúng tôi sẽ chứng minh ở đây những điều sau:
- Hệ thập phân đến Hệ cơ sở khác
- Hệ cơ sở khác sang thập phân
- Hệ cơ sở khác sang không thập phân
- Phương pháp phím tắt - Nhị phân đến Bát phân
- Phương thức phím tắt - Bát phân sang Nhị phân
- Phương pháp phím tắt - Nhị phân sang Thập lục phân
- Phương thức phím tắt - Hệ thập lục phân sang Nhị phân
Hệ thập phân đến Hệ cơ sở khác
Các bước
Step 1 - Chia số thập phân cần chuyển cho giá trị của cơ số mới.
Step 2 - Lấy phần dư từ Bước 1 là chữ số tận cùng bên phải (chữ số có nghĩa nhỏ nhất) của số cơ sở mới.
Step 3 - Chia thương của lần chia trước cho cơ số mới.
Step 4 - Ghi số dư từ Bước 3 là chữ số tiếp theo (bên trái) của số cơ sở mới.
Lặp lại các bước 3 và 4, lấy các phần còn lại từ phải sang trái, cho đến khi thương số trở thành 0 ở Bước 3.
Phần còn lại cuối cùng do đó thu được sẽ là Chữ số quan trọng nhất (MSD) của số cơ sở mới.
Ví dụ -
Số thập phân: 29 10
Tính toán tương đương nhị phân -
| Bươc | Hoạt động | Kết quả | Phần còn lại |
|---|---|---|---|
| Bước 1 | 29/2 | 14 | 1 |
| Bước 2 | 14/2 | 7 | 0 |
| Bước 3 | 7/2 | 3 | 1 |
| Bước 4 | 3/2 | 1 | 1 |
| Bước 5 | 1/2 | 0 | 1 |
Như đã đề cập trong Bước 2 và 4, phần còn lại phải được sắp xếp theo thứ tự ngược lại để phần còn lại đầu tiên trở thành Chữ số có ý nghĩa thấp nhất (LSD) và phần còn lại cuối cùng trở thành Chữ số quan trọng nhất (MSD).
Số thập phân - 29 10 = Số nhị phân - 11101 2 .
Hệ cơ sở khác sang hệ thập phân
Các bước
Step 1 - Xác định giá trị cột (vị trí) của mỗi chữ số (điều này phụ thuộc vào vị trí của chữ số và cơ số của hệ thống số).
Step 2 - Nhân các giá trị cột thu được (ở Bước 1) với các chữ số ở các cột tương ứng.
Step 3 - Tính tổng các tích đã tính ở Bước 2. Tổng là giá trị tương đương dưới dạng thập phân.
Thí dụ
Số nhị phân - 11101 2
Tính tương đương thập phân -
| Bươc | Số nhị phân | Số thập phân |
|---|---|---|
| Bước 1 | 11101 2 | ((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| Bước 2 | 11101 2 | (16 + 8 + 4 + 0 + 1) 10 |
| Bước 3 | 11101 2 | 29 10 |
Số nhị phân - 11101 2 = Số thập phân - 29 10
Hệ thống cơ sở khác đến hệ thống không thập phân
Các bước
Step 1 - Chuyển số ban đầu thành số thập phân (cơ số 10).
Step 2 - Chuyển số thập phân có được sang cơ số mới.
Thí dụ
Số bát phân - 25 8
Tính toán tương đương nhị phân -
Bước 1 - Chuyển đổi sang thập phân
| Bươc | Số bát phân | Số thập phân |
|---|---|---|
| Bước 1 | 25 8 | ((2 × 8 1 ) + (5 × 8 0 )) 10 |
| Bước 2 | 25 8 | (16 + 5) 10 |
| Bước 3 | 25 8 | 21 10 |
Số bát phân - 25 8 = Số thập phân - 21 10
Bước 2 - Chuyển đổi thập phân sang nhị phân
| Bươc | Hoạt động | Kết quả | Phần còn lại |
|---|---|---|---|
| Bước 1 | 21/2 | 10 | 1 |
| Bước 2 | 10/2 | 5 | 0 |
| Bước 3 | 5/2 | 2 | 1 |
| Bước 4 | 2/2 | 1 | 0 |
| Bước 5 | 1/2 | 0 | 1 |
Số thập phân - 21 10 = Số nhị phân - 10101 2
Số bát phân - 25 8 = Số nhị phân - 10101 2
Phương pháp phím tắt - Nhị phân đến Bát phân
Các bước
Step 1 - Chia các chữ số nhị phân thành các nhóm ba (bắt đầu từ bên phải).
Step 2 - Chuyển mỗi nhóm gồm ba chữ số nhị phân sang một chữ số bát phân.
Thí dụ
Số nhị phân - 10101 2
Tính tương đương hệ bát phân -
| Bươc | Số nhị phân | Số bát phân |
|---|---|---|
| Bước 1 | 10101 2 | 010 101 |
| Bước 2 | 10101 2 | 2 8 5 8 |
| Bước 3 | 10101 2 | 25 8 |
Số nhị phân - 10101 2 = Số bát phân - 25 8
Phương thức phím tắt - Bát phân sang Nhị phân
Các bước
Step 1 - Chuyển đổi mỗi chữ số bát phân thành số nhị phân 3 chữ số (các chữ số bát phân có thể được coi là số thập phân cho chuyển đổi này).
Step 2 - Kết hợp tất cả các nhóm nhị phân kết quả (mỗi nhóm có 3 chữ số) thành một số nhị phân duy nhất.
Thí dụ
Số bát phân - 25 8
Tính toán tương đương nhị phân -
| Bươc | Số bát phân | Số nhị phân |
|---|---|---|
| Bước 1 | 25 8 | 2 10 5 10 |
| Bước 2 | 25 8 | 010 2 101 2 |
| Bước 3 | 25 8 | 010101 2 |
Số bát phân - 25 8 = Số nhị phân - 10101 2
Phương pháp phím tắt - Nhị phân sang Thập lục phân
Các bước
Step 1 - Chia các chữ số nhị phân thành các nhóm bốn (bắt đầu từ bên phải).
Step 2 - Chuyển đổi mỗi nhóm bốn chữ số nhị phân sang một ký hiệu thập lục phân.
Thí dụ
Số nhị phân - 10101 2
Tính tương đương hệ thập lục phân -
| Bươc | Số nhị phân | Số thập lục phân |
|---|---|---|
| Bước 1 | 10101 2 | 0001 0101 |
| Bước 2 | 10101 2 | 1 10 5 10 |
| Bước 3 | 10101 2 | 15 16 |
Số nhị phân - 10101 2 = Số thập lục phân - 15 16
Phương thức phím tắt - Hệ thập lục phân sang Nhị phân
Các bước
Step 1 - Chuyển đổi mỗi chữ số thập lục phân thành số nhị phân 4 chữ số (các chữ số thập lục phân có thể được coi là số thập phân cho chuyển đổi này).
Step 2 - Kết hợp tất cả các nhóm nhị phân kết quả (mỗi nhóm 4 chữ số) thành một số nhị phân duy nhất.
Thí dụ
Số thập lục phân - 15 16
Tính toán tương đương nhị phân -
| Bươc | Số thập lục phân | Số nhị phân |
|---|---|---|
| Bước 1 | 15 16 | 1 10 5 10 |
| Bước 2 | 15 16 | 0001 2 0101 2 |
| Bước 3 | 15 16 | 00010101 2 |
Số thập lục phân - 15 16 = Số nhị phân - 10101 2
Trong mã hóa, khi số, chữ cái hoặc từ được biểu thị bằng một nhóm ký hiệu cụ thể, người ta nói rằng số, chữ cái hoặc từ đang được mã hóa. Nhóm ký hiệu được gọi là mã. Dữ liệu số được biểu diễn, lưu trữ và truyền dưới dạng nhóm các bit nhị phân. Nhóm này còn được gọi làbinary code. Mã nhị phân được biểu thị bằng số cũng như ký tự chữ và số.
Ưu điểm của mã nhị phân
Sau đây là danh sách những lợi thế mà mã nhị phân mang lại.
Mã nhị phân phù hợp với các ứng dụng máy tính.
Mã nhị phân phù hợp với truyền thông kỹ thuật số.
Mã nhị phân thực hiện việc phân tích và thiết kế các mạch kỹ thuật số nếu chúng ta sử dụng mã nhị phân.
Vì chỉ có 0 & 1 đang được sử dụng nên việc triển khai trở nên dễ dàng.
Phân loại mã nhị phân
Các mã được phân loại rộng rãi thành bốn loại sau.
- Mã trọng số
- Mã không trọng số
- Mã thập phân được mã hóa nhị phân
- Mã chữ và số
- Lỗi phát hiện mã
- Mã sửa lỗi
Mã trọng số
Mã nhị phân có trọng số là những mã nhị phân tuân theo nguyên tắc trọng số vị trí. Mỗi vị trí của con số đại diện cho một trọng lượng cụ thể. Một số hệ thống mã được sử dụng để biểu thị các chữ số thập phân từ 0 đến 9. Trong các mã này, mỗi chữ số thập phân được biểu diễn bằng một nhóm bốn bit.
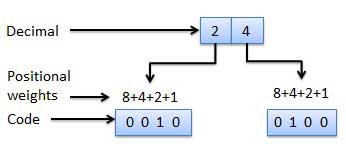
Mã không trọng số
Trong loại mã nhị phân này, trọng số vị trí không được ấn định. Các ví dụ về mã không trọng số là mã Thừa 3 và mã Xám.
Mã vượt quá 3
Mã Thừa 3 còn được gọi là mã XS-3. Nó là mã không trọng số được sử dụng để thể hiện số thập phân. Các từ mã thừa-3 được bắt nguồn từ 8421 từ mã BCD thêm (0011) 2 hoặc (3) 10 vào mỗi từ mã trong 8421. Các mã thừa-3 thu được như sau:

Thí dụ
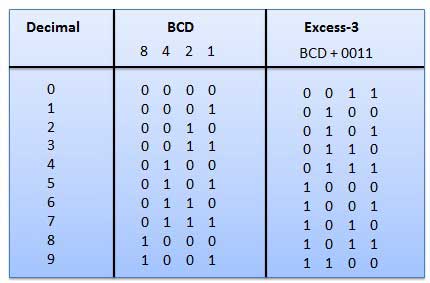
Mã màu xám
Nó là mã không trọng số và nó không phải là mã số học. Điều đó có nghĩa là không có trọng số cụ thể nào được gán cho vị trí bit. Nó có một tính năng rất đặc biệt là, chỉ một bit sẽ thay đổi mỗi khi số thập phân được tăng lên như trong hình. Khi chỉ một bit thay đổi tại một thời điểm, mã màu xám được gọi là mã khoảng cách đơn vị. Mã màu xám là mã tuần hoàn. Mã màu xám không thể được sử dụng cho phép toán số học.
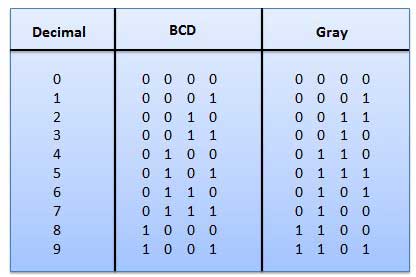
Ứng dụng của mã màu xám
Mã màu xám được sử dụng phổ biến trong các bộ mã hóa vị trí trục.
Bộ mã hóa vị trí trục tạo ra một từ mã đại diện cho vị trí góc của trục.
Mã số thập phân được mã hóa nhị phân (BCD)
Trong mã này, mỗi chữ số thập phân được biểu diễn bằng một số nhị phân 4 bit. BCD là một cách để thể hiện từng chữ số thập phân bằng mã nhị phân. Trong BCD, với bốn bit, chúng ta có thể biểu diễn mười sáu số (0000 đến 1111). Nhưng trong mã BCD chỉ có mười đầu tiên trong số này được sử dụng (0000 đến 1001). Sáu tổ hợp mã còn lại, tức là 1010 đến 1111 không hợp lệ trong BCD.
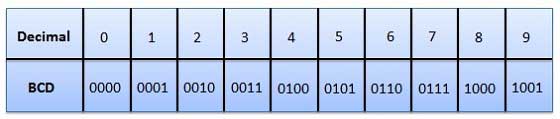
Ưu điểm của mã BCD
- Nó rất giống với hệ thống thập phân.
- Chúng ta chỉ cần nhớ nhị phân tương đương với các số thập phân từ 0 đến 9.
Nhược điểm của mã BCD
Phép cộng và phép trừ BCD có các quy tắc khác nhau.
Số học BCD phức tạp hơn một chút.
BCD cần số lượng bit nhiều hơn số nhị phân để biểu diễn số thập phân. Vì vậy, BCD kém hiệu quả hơn nhị phân.
Mã chữ và số
Một chữ số hoặc bit nhị phân chỉ có thể đại diện cho hai ký hiệu vì nó chỉ có hai trạng thái '0' hoặc '1'. Nhưng điều này là không đủ để giao tiếp giữa hai máy tính vì chúng ta cần nhiều ký hiệu khác để giao tiếp. Các ký hiệu này được yêu cầu đại diện cho 26 bảng chữ cái viết hoa và chữ nhỏ, các số từ 0 đến 9, dấu câu và các ký hiệu khác.
Mã chữ và số là mã biểu thị số và ký tự chữ cái. Hầu hết các mã như vậy cũng đại diện cho các ký tự khác như biểu tượng và các chỉ dẫn khác nhau cần thiết để truyền tải thông tin. Một mã chữ và số ít nhất phải đại diện cho 10 chữ số và 26 chữ cái trong bảng chữ cái, tức là tổng số 36 mục. Ba mã chữ và số sau đây rất thường được sử dụng để biểu diễn dữ liệu.
- Mã tiêu chuẩn Hoa Kỳ về trao đổi thông tin (ASCII).
- Mã trao đổi thập phân được mã hóa nhị phân mở rộng (EBCDIC).
- Mã Baudot năm bit.
Mã ASCII là mã 7 bit trong khi EBCDIC là mã 8 bit. Mã ASCII được sử dụng phổ biến hơn trên toàn thế giới trong khi EBCDIC được sử dụng chủ yếu trong các máy tính IBM lớn.
Mã lỗi
Có sẵn các kỹ thuật mã nhị phân để phát hiện và sửa dữ liệu trong quá trình truyền dữ liệu.
| Mã lỗi | Sự miêu tả |
|---|---|
Phát hiện và sửa lỗi |
Kỹ thuật phát hiện lỗi và sửa mã |
Có nhiều phương pháp hoặc kỹ thuật có thể được sử dụng để chuyển đổi mã từ định dạng này sang định dạng khác. Chúng tôi sẽ chứng minh ở đây những điều sau
- Chuyển đổi nhị phân sang BCD
- Chuyển đổi BCD sang Binary
- BCD đến Vượt quá-3
- Vượt quá-3 thành BCD
Chuyển đổi nhị phân sang BCD
Các bước
Step 1 - Chuyển số nhị phân sang số thập phân.
Step 2 - Chuyển số thập phân sang BCD.
Ví dụ - chuyển đổi (11101) 2 sang BCD.
Bước 1 - Chuyển đổi sang thập phân
Số nhị phân - 11101 2
Tính tương đương thập phân -
| Bươc | Số nhị phân | Số thập phân |
|---|---|---|
| Bước 1 | 11101 2 | ((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| Bước 2 | 11101 2 | (16 + 8 + 4 + 0 + 1) 10 |
| Bước 3 | 11101 2 | 29 10 |
Số nhị phân - 11101 2 = Số thập phân - 29 10
Bước 2 - Chuyển đổi sang BCD
Số thập phân - 29 10
Tính BCD Tương đương. Chuyển từng chữ số thành các nhóm gồm bốn chữ số nhị phân tương đương.
| Bươc | Số thập phân | Chuyển đổi |
|---|---|---|
| Bước 1 | 29 10 | 0010 2 1001 2 |
| Bước 2 | 29 10 | 00101001 BCD |
Kết quả
(11101)2 = (00101001)BCDChuyển đổi BCD sang Binary
Các bước
Step 1 - Chuyển số BCD sang số thập phân.
Step 2 - Chuyển đổi thập phân sang nhị phân.
Ví dụ - chuyển đổi (00101001) BCD sang Binary.
Bước 1 - Chuyển đổi sang BCD
Số BCD - (00101001) BCD
Tính tương đương thập phân. Chuyển mỗi bốn chữ số thành một nhóm và nhận được số thập phân tương đương cho mỗi nhóm.
| Bươc | Số BCD | Chuyển đổi |
|---|---|---|
| Bước 1 | (00101001) BCD | 0010 2 1001 2 |
| Bước 2 | (00101001) BCD | 2 10 9 10 |
| Bước 3 | (00101001) BCD | 29 10 |
Số BCD - (00101001) BCD = Số thập phân - 29 10
Bước 2 - Chuyển đổi sang Binary
Đã sử dụng phương pháp chia dài để chuyển đổi từ thập phân sang nhị phân.
Số thập phân - 29 10
Tính toán tương đương nhị phân -
| Bươc | Hoạt động | Kết quả | Phần còn lại |
|---|---|---|---|
| Bước 1 | 29/2 | 14 | 1 |
| Bước 2 | 14/2 | 7 | 0 |
| Bước 3 | 7/2 | 3 | 1 |
| Bước 4 | 3/2 | 1 | 1 |
| Bước 5 | 1/2 | 0 | 1 |
Như đã đề cập trong Bước 2 và 4, các phần còn lại phải được sắp xếp theo thứ tự ngược lại để phần dư đầu tiên trở thành chữ số có nghĩa nhỏ nhất (LSD) và phần dư cuối cùng trở thành chữ số có nghĩa nhất (MSD).
Số thập phân - 29 10 = Số nhị phân - 11101 2
Kết quả
(00101001)BCD = (11101)2BCD đến Vượt quá-3
Các bước
Step 1 - Chuyển đổi BCD sang số thập phân.
Step 2- Cộng (3) 10 vào số thập phân này.
Step 3 - Chuyển đổi thành nhị phân để lấy mã vượt quá-3.
Ví dụ - chuyển đổi (0110) BCD thành Dư-3.
Bước 1 - Chuyển đổi sang số thập phân
(0110) BCD = 6 10
Bước 2 - Thêm 3 vào số thập phân
(6) 10 + (3) 10 = (9) 10
Bước 3 - Chuyển đổi thành Thừa-3
(9) 10 = (1001) 2
Kết quả
(0110)BCD = (1001)XS-3Chuyển đổi vượt quá 3 sang BCD
Các bước
Step 1- Trừ (0011) 2 cho mỗi chữ số dư thừa 3 4 bit để được mã BCD tương ứng.
Ví dụ - chuyển đổi (10011010) XS-3 sang BCD.
Given XS-3 number = 1 0 0 1 1 0 1 0
Subtract (0011)2 = 1 0 0 1 0 1 1 1
--------------------
BCD = 0 1 1 0 0 1 1 1Kết quả
(10011010)XS-3 = (01100111)BCDPhần bổ sung được sử dụng trong máy tính kỹ thuật số để đơn giản hóa hoạt động trừ và cho các thao tác logic. Đối với mỗi hệ cơ số r (cơ số r đại diện cho cơ số của hệ thống số) có hai loại bổ sung.
| SN | Bổ sung | Sự miêu tả |
|---|---|---|
| 1 | Radix bổ sung | Phần bù cơ số được gọi là phần bù của r |
| 2 | Bổ sung Radix nhỏ | Phần bù cơ số giảm dần được gọi là phần bù của (r-1) |
Hệ thống nhị phân bổ sung
Vì hệ nhị phân có cơ số r = 2. Vì vậy hai loại phần bù của hệ nhị phân là phần bù của 2 và phần bù của 1.
Phần bổ sung của 1
Phần bù 1 của một số được tìm thấy bằng cách đổi tất cả các số 1 thành số 0 và tất cả các số 0 thành số 1. Điều này được gọi là lấy phần bổ sung hoặc phần bổ sung của 1. Ví dụ về Phần bổ sung của 1 như sau.
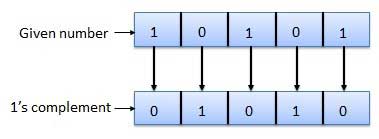
Bổ sung của 2
Phần bù 2 của số nhị phân thu được bằng cách thêm 1 vào Bit ít có ý nghĩa nhất (LSB) của phần bù 1 của số.
Phần bù của 2 = phần bù của 1 + 1
Ví dụ về Sự bổ sung của 2 như sau.
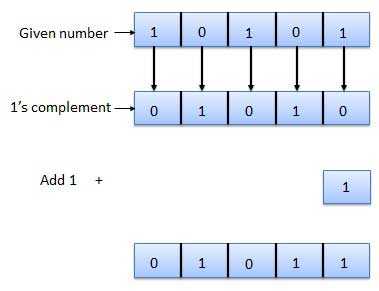
Số học nhị phân là một phần thiết yếu của tất cả các máy tính kỹ thuật số và nhiều hệ thống kỹ thuật số khác.
Phép cộng nhị phân
Nó là một chìa khóa cho phép trừ nhị phân, phép nhân, phép chia. Có bốn quy tắc cộng nhị phân.
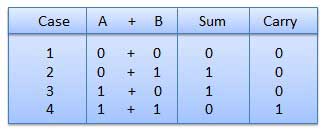
Trong trường hợp thứ tư, một phép cộng nhị phân đang tạo ra một tổng của (1 + 1 = 10) tức là 0 được viết trong cột đã cho và chuyển 1 sang cột tiếp theo.
Ví dụ - Phép cộng
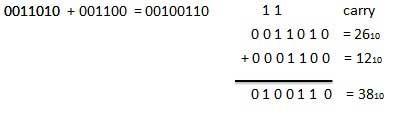
Phép trừ nhị phân
Subtraction and Borrow, hai từ này sẽ được sử dụng rất thường xuyên cho phép trừ nhị phân. Có bốn quy tắc của phép trừ nhị phân.
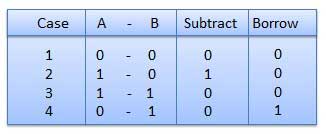
Ví dụ - Phép trừ
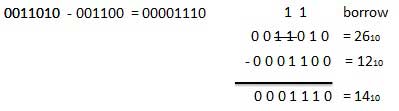
Phép nhân nhị phân
Phép nhân nhị phân tương tự như phép nhân thập phân. Nó đơn giản hơn phép nhân thập phân vì chỉ có 0 và 1 có liên quan. Có bốn quy tắc nhân nhị phân.
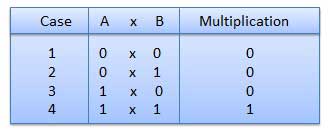
Ví dụ - Phép nhân

Bộ phận nhị phân
Phép chia nhị phân tương tự như phép chia thập phân. Nó được gọi là thủ tục phân chia dài.
Ví dụ - Phép chia

Hệ thống số bát phân
Sau đây là các đặc điểm của hệ thống số bát phân.
Sử dụng tám chữ số 0,1,2,3,4,5,6,7.
Còn được gọi là hệ cơ số 8.
Mỗi vị trí trong một số bát phân đại diện cho một lũy thừa 0 của cơ số (8). Ví dụ: 8 0
Vị trí cuối cùng trong một số bát phân thể hiện lũy thừa x của cơ số (8). Ví dụ: 8 x trong đó x đại diện cho vị trí cuối cùng - 1.
Thí dụ
Số bát phân - 12570 8
Tính tương đương thập phân -
| Bươc | Số bát phân | Số thập phân |
|---|---|---|
| Bước 1 | 12570 8 | ((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10 |
| Bước 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| Bước 3 | 12570 8 | 5496 10 |
Note −12570 8 thường được viết là 12570.
Phép cộng hệ bát phân
Bảng cộng bát phân sau đây sẽ giúp bạn xử lý phép cộng bát phân.

Để sử dụng bảng này, chỉ cần làm theo hướng dẫn được sử dụng trong ví dụ này: Thêm 6 8 và 5 8 . Xác định vị trí 6 trong cột A sau đó xác định vị trí 5 trong cột B. Điểm trong vùng 'tổng' nơi hai cột này giao nhau là 'tổng' của hai số.
68 + 58 = 138.Ví dụ - Phép cộng
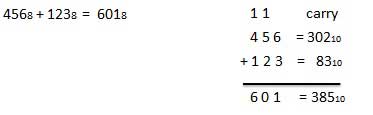
Phép trừ bát phân
Phép trừ các số bát phân tuân theo các quy tắc tương tự như phép trừ các số trong bất kỳ hệ thống số nào khác. Sự thay đổi duy nhất là số mượn. Trong hệ thập phân, bạn mượn một nhóm 10 10 . Trong hệ thống nhị phân, bạn mượn một nhóm 2 10 . Trong hệ bát phân, bạn mượn một nhóm 8 10 .
Ví dụ - Phép trừ
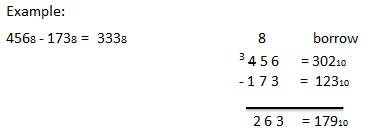
Hệ thống số thập lục phân
Sau đây là các đặc điểm của hệ thống số thập lục phân.
Sử dụng 10 chữ số và 6 chữ cái, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
Các chữ cái đại diện cho các số bắt đầu từ 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Còn được gọi là hệ cơ số 16.
Mỗi vị trí trong một số thập lục phân đại diện cho một lũy thừa 0 của cơ số (16). Ví dụ - 16 0
Vị trí cuối cùng trong một số thập lục phân thể hiện lũy thừa x của cơ số (16). Ví dụ - 16 x trong đó x đại diện cho vị trí cuối cùng - 1.
Thí dụ
Số thập lục phân - 19FDE 16
Tính tương đương thập phân -
| Bươc | Số thập lục phân | Số thập phân |
|---|---|---|
| Bước 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Bước 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| Bước 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| Bước 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 thường được viết là 19FDE.
Phép cộng hệ thập lục phân
Bảng cộng hệ thập lục phân sau đây sẽ giúp bạn rất nhiều để xử lý phép cộng hệ thập lục phân.
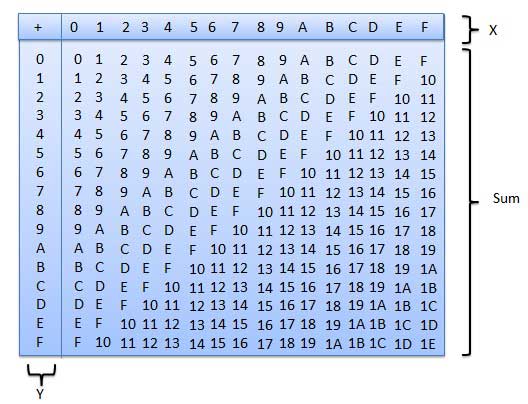
Để sử dụng bảng này, chỉ cần làm theo hướng dẫn được sử dụng trong ví dụ này - Thêm A 16 và 5 16 . Xác định vị trí A trong cột X sau đó xác định vị trí 5 trong cột Y. Điểm trong vùng 'tổng' nơi hai cột này giao nhau là tổng của hai số.
A16 + 516 = F16.Ví dụ - Phép cộng
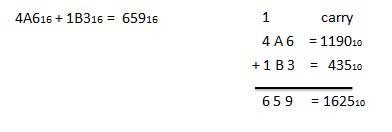
Phép trừ thập lục phân
Phép trừ các số thập lục phân tuân theo các quy tắc tương tự như phép trừ các số trong bất kỳ hệ thống số nào khác. Sự thay đổi duy nhất là số mượn. Trong hệ thập phân, bạn mượn một nhóm 10 10 . Trong hệ thống nhị phân, bạn mượn một nhóm 2 10 . Trong hệ thập lục phân, bạn mượn một nhóm 16 10 .
Ví dụ - Phép trừ

Boolean Algebra được sử dụng để phân tích và đơn giản hóa các mạch số (logic). Nó chỉ sử dụng các số nhị phân tức là 0 và 1. Nó còn được gọi làBinary Algebra hoặc là logical Algebra. Đại số Boolean được phát minh bởiGeorge Boole vào năm 1854.
Quy tắc trong Đại số Boolean
Sau đây là các quy tắc quan trọng được sử dụng trong đại số Boolean.
Biến được sử dụng chỉ có thể có hai giá trị. Nhị phân 1 cho CAO và Nhị phân 0 cho THẤP.
Phần bổ sung của một biến được biểu diễn bằng dấu gạch ngang (-). Do đó, phần bù của biến B được biểu diễn dưới dạng
. Do đó nếu B = 0 thì = 1 và B = 1 thì
= 1 và B = 1 thì = 0.
= 0.
ORing của các biến được biểu diễn bằng dấu cộng (+) giữa chúng. Ví dụ ORing của A, B, C được biểu diễn là A + B + C.
Hàm AND logic của hai hoặc nhiều biến được biểu diễn bằng cách viết một dấu chấm giữa chúng, chẳng hạn như ABC Đôi khi dấu chấm có thể bị bỏ qua như ABC.
Luật Boolean
Có sáu loại Luật Boolean.
Luật thay thế
Bất kỳ phép toán nhị phân nào thỏa mãn biểu thức sau được gọi là phép toán giao hoán.

Luật giao hoán phát biểu rằng việc thay đổi trình tự của các biến không có bất kỳ ảnh hưởng nào đến đầu ra của mạch logic.
Luật kết hợp
Luật này tuyên bố rằng thứ tự thực hiện các thao tác logic là không liên quan vì tác dụng của chúng là như nhau.
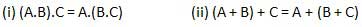
Luật phân phối
Luật phân phối phát biểu điều kiện sau.
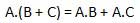
Luật VÀ
Các luật này sử dụng phép toán AND. Do đó chúng được gọi làAND luật.
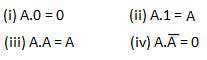
HOẶC luật
Các luật này sử dụng phép toán OR. Do đó chúng được gọi làOR luật.
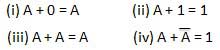
Luật ĐẦU TƯ
Luật này sử dụng phép toán NOT. Luật nghịch đảo phát biểu rằng đảo đôi một biến dẫn đến chính biến ban đầu.
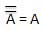
Định lý Boolean quan trọng
Sau đây là một vài Định lý boolean quan trọng.
| Hàm / định lý Boolean | Sự miêu tả |
|---|---|
Hàm Boolean |
Các hàm và biểu thức Boolean, K-Map và NAND Gates hiện thực hóa |
Định lý De Morgan |
Định lý De Morgan 1 và Định lý 2 |
Cổng logic là khối xây dựng cơ bản của bất kỳ hệ thống kỹ thuật số nào. Nó là một mạch điện tử có một hoặc nhiều hơn một đầu vào và chỉ một đầu ra. Mối quan hệ giữa đầu vào và đầu ra dựa trêncertain logic. Dựa trên điều này, các cổng logic được đặt tên là cổng VÀ, cổng HOẶC, cổng KHÔNG, v.v.
Và cổng
Một mạch thực hiện phép toán AND được thể hiện trong hình. Nó có n đầu vào (n> = 2) và một đầu ra.

Sơ đồ logic
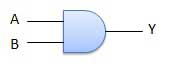
Bảng sự thật
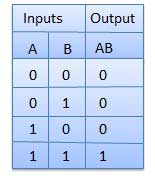
HOẶC Cổng
Một mạch thực hiện phép OR được thể hiện trong hình. Nó có n đầu vào (n> = 2) và một đầu ra.
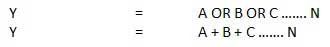
Sơ đồ logic
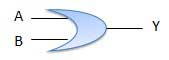
Bảng sự thật
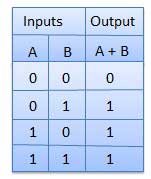
Cổng KHÔNG
Cổng NOT còn được gọi là Inverter. Nó có một đầu vào A và một đầu ra Y.
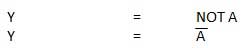
Sơ đồ logic
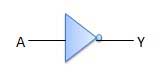
Bảng sự thật
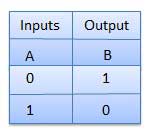
Cổng NAND
Hoạt động NOT-AND được gọi là hoạt động NAND. Nó có n đầu vào (n> = 2) và một đầu ra.
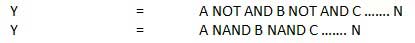
Sơ đồ logic
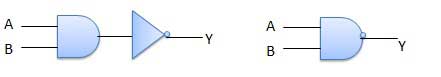
Bảng sự thật
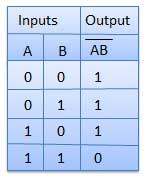
Cổng NOR
Phép toán NOT-OR được gọi là phép toán NOR. Nó có n đầu vào (n> = 2) và một đầu ra.
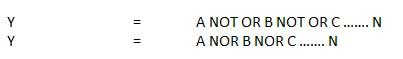
Sơ đồ logic
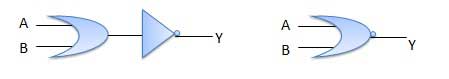
Bảng sự thật
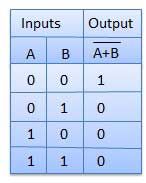
Cổng XOR
Cổng XOR hoặc Ex-OR là một loại cổng đặc biệt. Nó có thể được sử dụng trong bộ cộng một nửa, bộ cộng đầy đủ và bộ trừ. Cổng OR-độc quyền được viết tắt là cổng EX-OR hoặc đôi khi là cổng X-OR. Nó có n đầu vào (n> = 2) và một đầu ra.
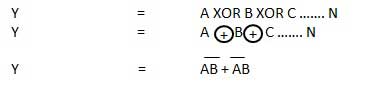
Sơ đồ logic
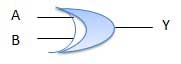
Bảng sự thật
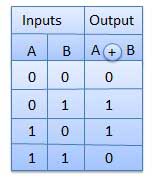
Cổng XNOR
Cổng XNOR là loại cổng đặc biệt. Nó có thể được sử dụng trong bộ cộng một nửa, bộ cộng đầy đủ và bộ trừ. Cổng NOR độc quyền được viết tắt là cổng EX-NOR hoặc đôi khi là cổng X-NOR. Nó có n đầu vào (n> = 2) và một đầu ra.
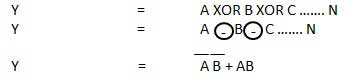
Sơ đồ logic
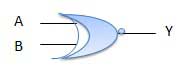
Bảng sự thật
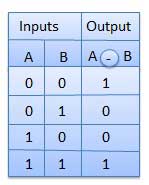
Mạch kết hợp là mạch trong đó chúng ta kết hợp các cổng khác nhau trong mạch, ví dụ bộ mã hóa, bộ giải mã, bộ ghép kênh và bộ phân kênh. Một số đặc điểm của mạch tổ hợp là:
Đầu ra của mạch tổ hợp tại bất kỳ thời điểm nào, chỉ phụ thuộc vào các mức hiện diện tại các thiết bị đầu cuối đầu vào.
Mạch tổ hợp không sử dụng bất kỳ bộ nhớ nào. Trạng thái trước đó của đầu vào không có bất kỳ ảnh hưởng nào đến trạng thái hiện tại của mạch.
Một mạch tổ hợp có thể có n số đầu vào và m số đầu ra.
Sơ đồ khối
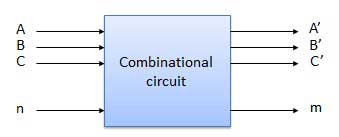
Chúng ta sẽ giải thích một số mạch tổ hợp quan trọng như sau.
Một nửa Adder
Bộ cộng nửa là một mạch logic tổ hợp với hai đầu vào và hai đầu ra. Mạch cộng một nửa được thiết kế để thêm hai số nhị phân bit đơn A và B. Nó là khối xây dựng cơ bản để cộng haisinglesố bit. Mạch này có hai đầu racarry và sum.
Sơ đồ khối

Bảng sự thật
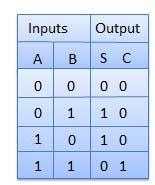
Sơ đồ mạch
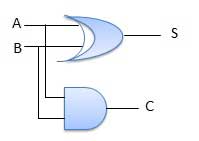
Adder đầy đủ
Bộ cộng đầy đủ được phát triển để khắc phục nhược điểm của mạch Half Adder. Nó có thể thêm hai số một bit A và B, và mang c. Bộ cộng đầy đủ là một mạch tổ hợp ba đầu vào và hai đầu ra.
Sơ đồ khối

Bảng sự thật
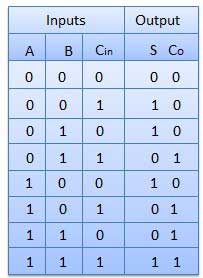
Sơ đồ mạch
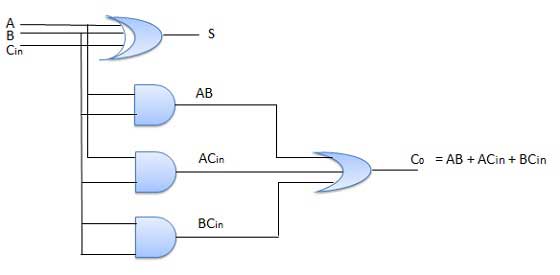
Trình quảng cáo song song N-Bit
Full Adder chỉ có thể thêm hai số nhị phân một chữ số cùng với một đầu vào mang. Nhưng trong thực tế, chúng ta cần thêm các số nhị phân dài hơn chỉ một bit. Để thêm hai số nhị phân n-bit, chúng ta cần sử dụng bộ cộng song song n-bit. Nó sử dụng một số bộ cộng đầy đủ theo tầng. Đầu ra mang của bộ cộng đầy đủ trước đó được kết nối với đầu vào mang của bộ cộng đầy đủ tiếp theo.
Trình quảng cáo song song 4 bit
Trong sơ đồ khối, A 0 và B 0 đại diện cho LSB của bốn từ bit A và B. Do đó Full Adder-0 là giai đoạn thấp nhất. Do đó C trong của nó đã vĩnh viễn được tạo thành 0. Phần còn lại của các kết nối giống hệt như kết nối của bộ cộng song song n-bit được thể hiện trong hình. Bộ cộng song song bốn bit là một mạch logic rất phổ biến.
Sơ đồ khối

Dấu trừ song song N-Bit
Phép trừ có thể được thực hiện bằng cách lấy phần bù 1 hoặc 2 của số bị trừ. Ví dụ, chúng ta có thể thực hiện phép trừ (AB) bằng cách thêm phần bù 1 hoặc 2 của B vào A. Điều đó có nghĩa là chúng ta có thể sử dụng bộ cộng nhị phân để thực hiện phép trừ nhị phân.
Dấu trừ song song 4 bit
Đầu tiên số bị trừ (B) được chuyển qua các bộ nghịch lưu để lấy phần bù 1 của nó. Sau đó, bộ cộng 4 bit sẽ thêm phần bù của A và 2 của B để tạo ra phép trừ. S 3 S 2 S 1 S 0 đại diện cho kết quả của phép trừ nhị phân (AB) và thực hiện đầu ra C ra đại diện cho cực của kết quả. Nếu A> B thì Cout = 0 và kết quả ở dạng nhị phân (AB) thì C out = 1 và kết quả ở dạng bù 2.
Block diagram
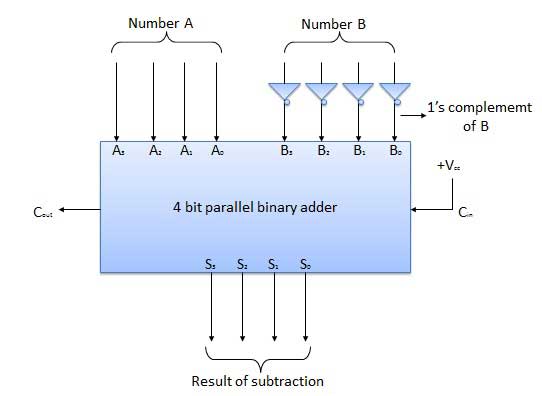
Half Subtractors
Half subtractor is a combination circuit with two inputs and two outputs (difference and borrow). It produces the difference between the two binary bits at the input and also produces an output (Borrow) to indicate if a 1 has been borrowed. In the subtraction (A-B), A is called as Minuend bit and B is called as Subtrahend bit.
Truth Table
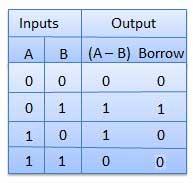
Circuit Diagram
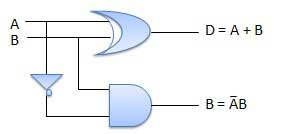
Full Subtractors
The disadvantage of a half subtractor is overcome by full subtractor. The full subtractor is a combinational circuit with three inputs A,B,C and two output D and C'. A is the 'minuend', B is 'subtrahend', C is the 'borrow' produced by the previous stage, D is the difference output and C' is the borrow output.
Truth Table
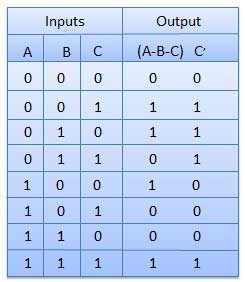
Circuit Diagram
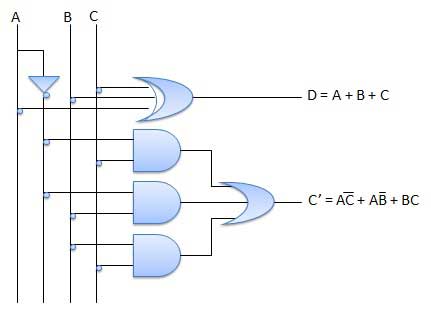
Multiplexers
Multiplexer is a special type of combinational circuit. There are n-data inputs, one output and m select inputs with 2m = n. It is a digital circuit which selects one of the n data inputs and routes it to the output. The selection of one of the n inputs is done by the selected inputs. Depending on the digital code applied at the selected inputs, one out of n data sources is selected and transmitted to the single output Y. E is called the strobe or enable input which is useful for the cascading. It is generally an active low terminal that means it will perform the required operation when it is low.
Block diagram
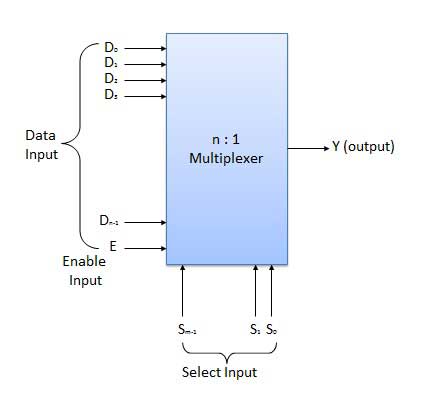
Multiplexers come in multiple variations
- 2 : 1 multiplexer
- 4 : 1 multiplexer
- 16 : 1 multiplexer
- 32 : 1 multiplexer
Block Diagram
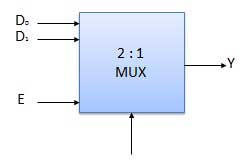
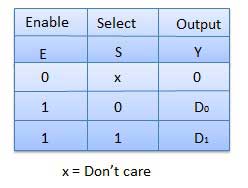
Truth Table
Demultiplexers
A demultiplexer performs the reverse operation of a multiplexer i.e. it receives one input and distributes it over several outputs. It has only one input, n outputs, m select input. At a time only one output line is selected by the select lines and the input is transmitted to the selected output line. A de-multiplexer is equivalent to a single pole multiple way switch as shown in fig.
Demultiplexers comes in multiple variations.
- 1 : 2 demultiplexer
- 1 : 4 demultiplexer
- 1 : 16 demultiplexer
- 1 : 32 demultiplexer
Block diagram
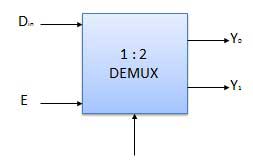
Truth Table
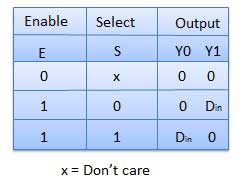
Decoder
A decoder is a combinational circuit. It has n input and to a maximum m = 2n outputs. Decoder is identical to a demultiplexer without any data input. It performs operations which are exactly opposite to those of an encoder.
Block diagram

Examples of Decoders are following.
- Code converters
- BCD to seven segment decoders
- Nixie tube decoders
- Relay actuator
2 to 4 Line Decoder
The block diagram of 2 to 4 line decoder is shown in the fig. A and B are the two inputs where D through D are the four outputs. Truth table explains the operations of a decoder. It shows that each output is 1 for only a specific combination of inputs.
Block diagram

Truth Table

Logic Circuit
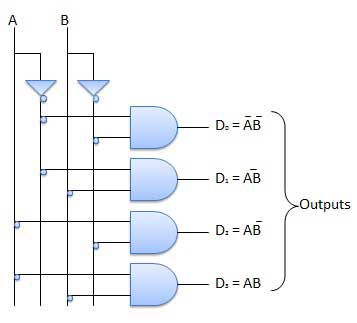
Encoder
Encoder is a combinational circuit which is designed to perform the inverse operation of the decoder. An encoder has n number of input lines and m number of output lines. An encoder produces an m bit binary code corresponding to the digital input number. The encoder accepts an n input digital word and converts it into an m bit another digital word.
Block diagram
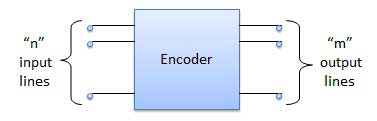
Examples of Encoders are following.
- Priority encoders
- Decimal to BCD encoder
- Octal to binary encoder
- Hexadecimal to binary encoder
Priority Encoder
This is a special type of encoder. Priority is given to the input lines. If two or more input line are 1 at the same time, then the input line with highest priority will be considered. There are four input D0, D1, D2, D3 and two output Y0, Y1. Out of the four input D3 has the highest priority and D0 has the lowest priority. That means if D3 = 1 then Y1 Y1 = 11 irrespective of the other inputs. Similarly if D3 = 0 and D2 = 1 then Y1 Y0 = 10 irrespective of the other inputs.
Block diagram

Truth Table
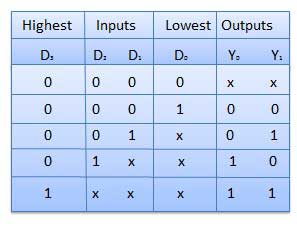
Logic Circuit
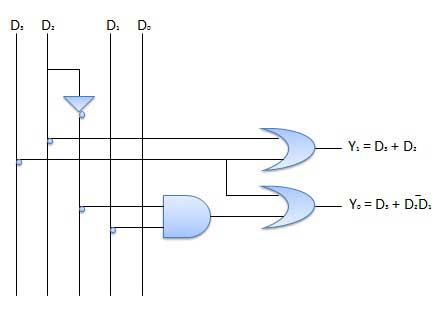
The combinational circuit does not use any memory. Hence the previous state of input does not have any effect on the present state of the circuit. But sequential circuit has memory so output can vary based on input. This type of circuits uses previous input, output, clock and a memory element.
Block diagram
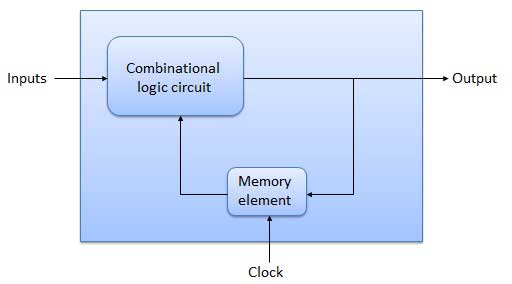
Flip Flop
Flip flop is a sequential circuit which generally samples its inputs and changes its outputs only at particular instants of time and not continuously. Flip flop is said to be edge sensitive or edge triggered rather than being level triggered like latches.
S-R Flip Flop
It is basically S-R latch using NAND gates with an additional enable input. It is also called as level triggered SR-FF. For this, circuit in output will take place if and only if the enable input (E) is made active. In short this circuit will operate as an S-R latch if E = 1 but there is no change in the output if E = 0.
Block Diagram
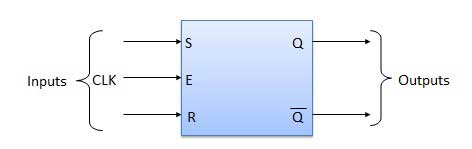
Circuit Diagram
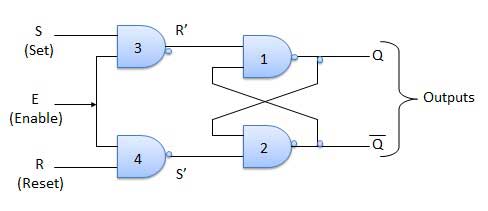
Truth Table
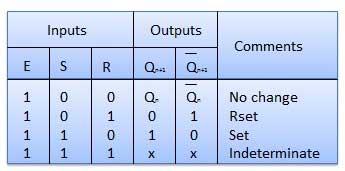
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | S = R = 0 : No change | If S = R = 0 then output of NAND gates 3 and 4 are forced to become 1. Hence R' and S' both will be equal to 1. Since S' and R' are the input of the basic S-R latch using NAND gates, there will be no change in the state of outputs. |
| 2 | S = 0, R = 1, E = 1 | Since S = 0, output of NAND-3 i.e. R' = 1 and E = 1 the output of NAND-4 i.e. S' = 0. Hence Qn+1 = 0 and Qn+1 bar = 1. This is reset condition. |
| 3 | S = 1, R = 0, E = 1 | Output of NAND-3 i.e. R' = 0 and output of NAND-4 i.e. S' = 1. Hence output of S-R NAND latch is Qn+1 = 1 and Qn+1 bar = 0. This is the reset condition. |
| 4 | S = 1, R = 1, E = 1 | As S = 1, R = 1 and E = 1, the output of NAND gates 3 and 4 both are 0 i.e. S' = R' = 0. Hence the Race condition will occur in the basic NAND latch. |
Master Slave JK Flip Flop
Master slave JK FF is a cascade of two S-R FF with feedback from the output of second to input of first. Master is a positive level triggered. But due to the presence of the inverter in the clock line, the slave will respond to the negative level. Hence when the clock = 1 (positive level) the master is active and the slave is inactive. Whereas when clock = 0 (low level) the slave is active and master is inactive.
Circuit Diagram
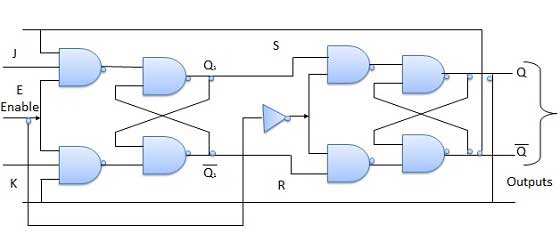
Truth Table
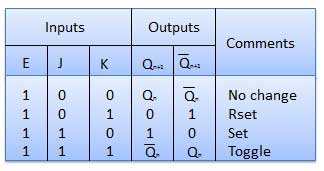
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | J = K = 0 (No change) | When clock = 0, the slave becomes active and master is inactive. But since the S and R inputs have not changed, the slave outputs will also remain unchanged. Therefore outputs will not change if J = K =0. |
| 2 | J = 0 and K = 1 (Reset) | Clock = 1 − Master active, slave inactive. Therefore outputs of the master become Q1 = 0 and Q1 bar = 1. That means S = 0 and R =1. Clock = 0 − Slave active, master inactive. Therefore outputs of the slave become Q = 0 and Q bar = 1. Again clock = 1 − Master active, slave inactive. Therefore even with the changed outputs Q = 0 and Q bar = 1 fed back to master, its output will be Q1 = 0 and Q1 bar = 1. That means S = 0 and R = 1. Hence with clock = 0 and slave becoming active the outputs of slave will remain Q = 0 and Q bar = 1. Thus we get a stable output from the Master slave. |
| 3 | J = 1 and K = 0 (Set) | Clock = 1 − Master active, slave inactive. Therefore outputs of the master become Q1 = 1 and Q1 bar = 0. That means S = 1 and R =0. Clock = 0 − Slave active, master inactive. Therefore outputs of the slave become Q = 1 and Q bar = 0. Again clock = 1 − then it can be shown that the outputs of the slave are stabilized to Q = 1 and Q bar = 0. |
| 4 | J = K = 1 (Toggle) | Clock = 1 − Master active, slave inactive. Outputs of master will toggle. So S and R also will be inverted. Clock = 0 − Slave active, master inactive. Outputs of slave will toggle. These changed output are returned back to the master inputs. But since clock = 0, the master is still inactive. So it does not respond to these changed outputs. This avoids the multiple toggling which leads to the race around condition. The master slave flip flop will avoid the race around condition. |
Delay Flip Flop / D Flip Flop
Delay Flip Flop or D Flip Flop is the simple gated S-R latch with a NAND inverter connected between S and R inputs. It has only one input. The input data is appearing at the output after some time. Due to this data delay between i/p and o/p, it is called delay flip flop. S and R will be the complements of each other due to NAND inverter. Hence S = R = 0 or S = R = 1, these input condition will never appear. This problem is avoid by SR = 00 and SR = 1 conditions.
Block Diagram
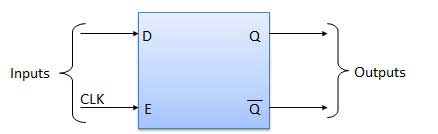
Circuit Diagram
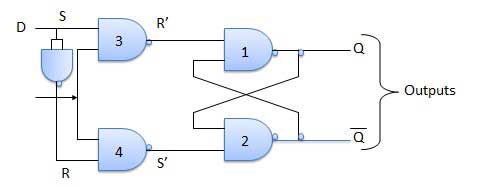
Truth Table
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | E = 0 | Latch is disabled. Hence no change in output. |
| 2 | E = 1 and D = 0 | If E = 1 and D = 0 then S = 0 and R = 1. Hence irrespective of the present state, the next state is Qn+1 = 0 and Qn+1 bar = 1. This is the reset condition. |
| 3 | E = 1 and D = 1 | If E = 1 and D = 1, then S = 1 and R = 0. This will set the latch and Qn+1 = 1 and Qn+1 bar = 0 irrespective of the present state. |
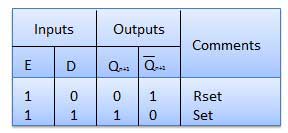
Toggle Flip Flop / T Flip Flop
Toggle flip flop is basically a JK flip flop with J and K terminals permanently connected together. It has only input denoted by T as shown in the Symbol Diagram. The symbol for positive edge triggered T flip flop is shown in the Block Diagram.
Symbol Diagram
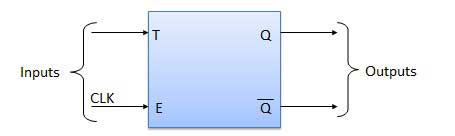
Block Diagram
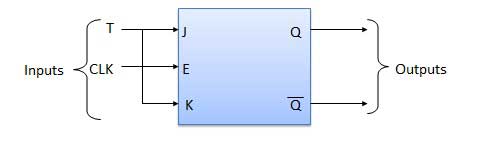
Truth Table
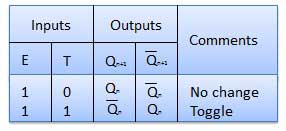
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | T = 0, J = K = 0 | The output Q and Q bar won't change |
| 2 | T = 1, J = K = 1 | Output will toggle corresponding to every leading edge of clock signal. |
Flip-flop is a 1 bit memory cell which can be used for storing the digital data. To increase the storage capacity in terms of number of bits, we have to use a group of flip-flop. Such a group of flip-flop is known as a Register. The n-bit register will consist of n number of flip-flop and it is capable of storing an n-bit word.
The binary data in a register can be moved within the register from one flip-flop to another. The registers that allow such data transfers are called as shift registers. There are four mode of operations of a shift register.
- Đầu vào nối tiếp Đầu ra nối tiếp
- Đầu vào nối tiếp Đầu ra song song
- Đầu vào song song Đầu ra nối tiếp
- Đầu vào song song Đầu ra song song
Đầu vào nối tiếp Đầu ra nối tiếp
Để tất cả các flip-flop ban đầu ở điều kiện thiết lập lại tức là Q 3 = Q 2 = Q 1 = Q 0 = 0. Nếu một mục nhập của số nhị phân 4 bit 1 1 1 1 được thực hiện vào thanh ghi, con số này sẽ là áp dụng choDinbit với bit LSB được áp dụng đầu tiên. Đầu vào D của FF-3 tức là D 3 được kết nối với đầu vào dữ liệu nối tiếpDin. Đầu ra của FF-3 tức là Q 3 được kết nối với đầu vào của flip-flop tiếp theo tức là D 2 , v.v.
Sơ đồ khối
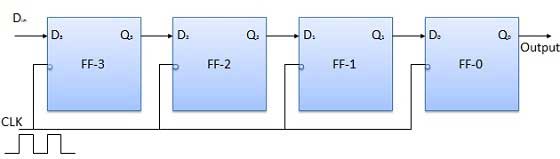
Hoạt động
Trước khi áp dụng tín hiệu đồng hồ, đặt Q 3 Q 2 Q 1 Q 0 = 0000 và áp dụng bit LSB của số được nhập vào D trong . Vậy D in = D 3 = 1. Áp dụng đồng hồ. Ở cạnh rơi đầu tiên của đồng hồ, FF-3 được thiết lập, và từ được lưu trữ trong thanh ghi là Q 3 Q 2 Q 1 Q 0 = 1000.
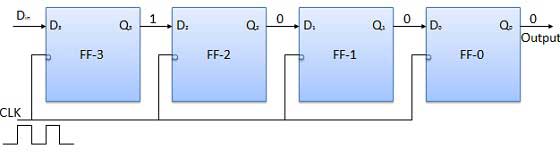
Áp dụng bit tiếp theo cho D trong . Vì vậy, D in = 1. Ngay sau khi cạnh âm tiếp theo của đồng hồ chạm vào, FF-2 sẽ thiết lập và từ được lưu trữ thay đổi thành Q 3 Q 2 Q 1 Q 0 = 1100.
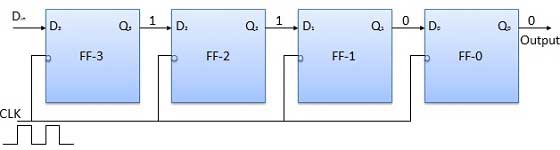
Áp dụng bit tiếp theo được lưu trữ tức là 1 đến D trong . Áp dụng xung đồng hồ. Ngay sau khi cạnh xung nhịp âm thứ ba chạm vào, FF-1 sẽ được thiết lập và đầu ra sẽ được sửa đổi thành Q 3 Q 2 Q 1 Q 0 = 1110.
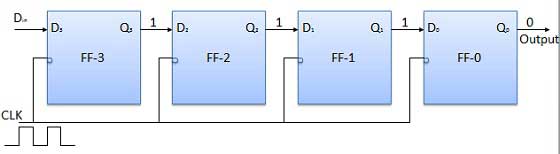
Tương tự với D in = 1 và với cạnh đồng hồ âm thứ tư đến, từ được lưu trữ trong thanh ghi là Q 3 Q 2 Q 1 Q 0 = 1111.
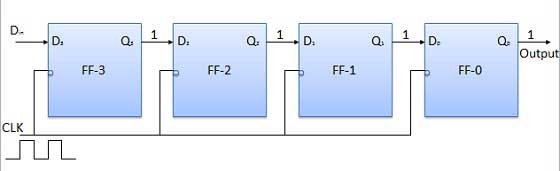
Bảng sự thật
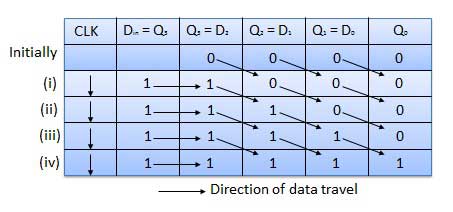
Dạng sóng

Đầu vào nối tiếp Đầu ra song song
Trong các kiểu hoạt động như vậy, dữ liệu được nhập theo thứ tự và lấy ra theo kiểu song song.
Dữ liệu được tải từng chút một. Các đầu ra bị vô hiệu hóa miễn là dữ liệu đang tải.
Ngay sau khi quá trình tải dữ liệu hoàn tất, tất cả các flip-flop chứa dữ liệu cần thiết của chúng, các đầu ra được kích hoạt để tất cả dữ liệu đã tải có sẵn trên tất cả các dòng đầu ra cùng một lúc.
Cần 4 chu kỳ đồng hồ để tải một từ bốn bit. Do đó tốc độ hoạt động của chế độ SIPO giống như tốc độ của chế độ SISO.
Sơ đồ khối
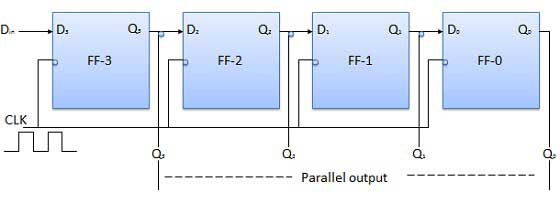
Đầu vào nối tiếp đầu vào song song (PISO)
Các bit dữ liệu được nhập theo kiểu song song.
Mạch hiển thị dưới đây là một thanh ghi đầu ra nối tiếp đầu vào song song bốn bit.
Đầu ra của Flip Flop trước được kết nối với đầu vào của Flip Flop tiếp theo thông qua mạch tổ hợp.
Từ đầu vào nhị phân B 0 , B 1 , B 2 , B 3 được áp dụng mặc dù cùng một mạch tổ hợp.
Có hai chế độ mà mạch này có thể hoạt động là - chế độ thay đổi hoặc chế độ tải.
Chế độ tải
Khi dòng shift / load bar ở mức thấp (0), cổng AND 2, 4 và 6 trở nên hoạt động, chúng sẽ chuyển các bit B 1 , B 2 , B 3 tới các flip-flops tương ứng. Ở mức thấp nhất của xung nhịp, đầu vào nhị phân B 0 , B 1 , B 2 , B 3 sẽ được tải vào các flip-flops tương ứng. Do đó quá trình tải song song diễn ra.
Chế độ thay đổi
Khi dòng thanh chuyển / tải ở mức thấp (1), cổng AND 2, 4 và 6 trở nên không hoạt động. Do đó, việc tải song song dữ liệu trở nên không thể. Nhưng cổng AND 1,3 và 5 trở nên hoạt động. Do đó, sự dịch chuyển dữ liệu từ trái sang phải từng bit dựa trên ứng dụng của xung đồng hồ. Vì vậy, song song trong hoạt động nối tiếp ra diễn ra.
Sơ đồ khối
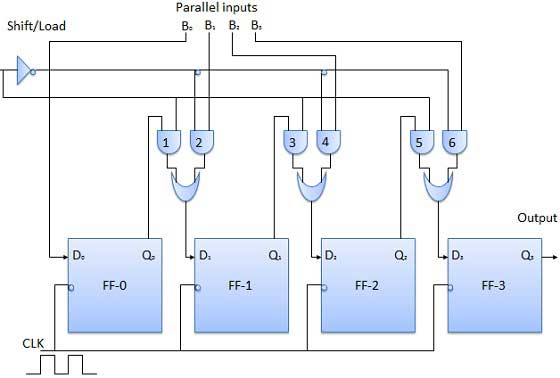
Đầu vào song song Đầu ra song song (PIPO)
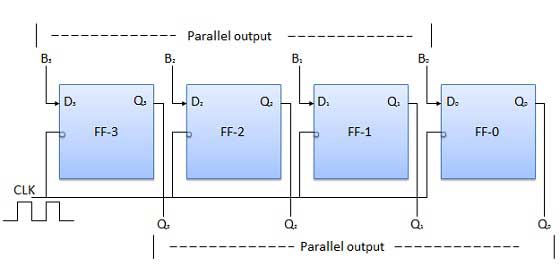
Trong chế độ này, đầu vào nhị phân 4 bit B 0 , B 1 , B 2 , B 3 được áp dụng cho các đầu vào dữ liệu D 0 , D 1 , D 2 , D 3 tương ứng của bốn flip-flop. Ngay sau khi một cạnh xung nhịp âm được áp dụng, các bit nhị phân đầu vào sẽ được tải đồng thời vào các flip-flop. Các bit được tải sẽ xuất hiện đồng thời ở phía đầu ra. Chỉ xung đồng hồ là cần thiết để tải tất cả các bit.
Sơ đồ khối
Đăng ký dịch chuyển hai chiều
Nếu một số nhị phân được dịch sang trái một vị trí thì nó tương đương với việc nhân số ban đầu với 2. Tương tự như vậy nếu một số nhị phân được dịch sang phải một vị trí thì nó tương đương với việc chia số ban đầu cho 2.
Do đó, nếu chúng ta muốn sử dụng thanh ghi shift để nhân và chia số nhị phân đã cho, thì chúng ta sẽ có thể di chuyển dữ liệu theo hướng trái hoặc phải.
Thanh ghi như vậy được gọi là thanh ghi hai chiều. Một thanh ghi dịch chuyển hai hướng bốn bit được hiển thị trong hình.
Có hai đầu vào nối tiếp là đầu vào dữ liệu dịch chuyển sang phải nối tiếp DR và đầu vào dữ liệu dịch chuyển sang trái nối tiếp DL cùng với đầu vào chọn chế độ (M).
Sơ đồ khối
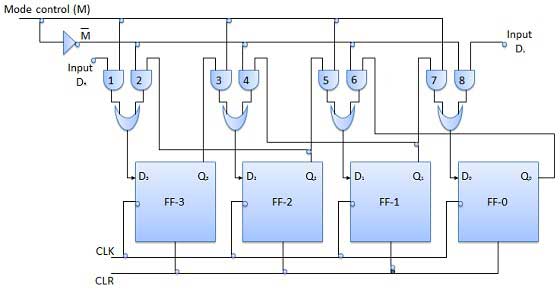
Hoạt động
| SN | Tình trạng | Hoạt động |
|---|---|---|
| 1 | With M = 1 − Shift right operation | Nếu M = 1, thì các cổng AND 1, 3, 5 và 7 được bật trong khi các cổng AND còn lại 2, 4, 6 và 8 sẽ bị vô hiệu hóa. Dữ liệu tại D R được chuyển sang phải từng bit từ FF-3 đến FF-0 trên ứng dụng của xung đồng hồ. Như vậy với M = 1 chúng ta nhận được phép toán dịch phải nối tiếp. |
| 2 | With M = 0 − Shift left operation | Khi điều khiển chế độ M được kết nối với 0 thì các cổng AND 2, 4, 6 và 8 được bật trong khi 1, 3, 5 và 7 bị tắt. Dữ liệu tại D L được chuyển sang trái từng bit từ FF-0 đến FF-3 trên ứng dụng của xung đồng hồ. Do đó với M = 0 chúng ta nhận được phép toán dịch phải nối tiếp. |
Đăng ký Universal Shift
Thanh ghi dịch chuyển có thể chuyển dữ liệu chỉ theo một hướng được gọi là thanh ghi dịch chuyển một hướng. Thanh ghi dịch chuyển có thể thay đổi dữ liệu theo cả hai hướng được gọi là thanh ghi dịch chuyển hai hướng. Áp dụng cùng một logic, một thanh ghi shift có thể dịch chuyển dữ liệu theo cả hai hướng cũng như tải nó song song, được gọi là thanh ghi dịch chuyển chung. Thanh ghi ca có thể thực hiện thao tác sau:
- Tải song song
- Dịch chuyển trái
- Sang phải
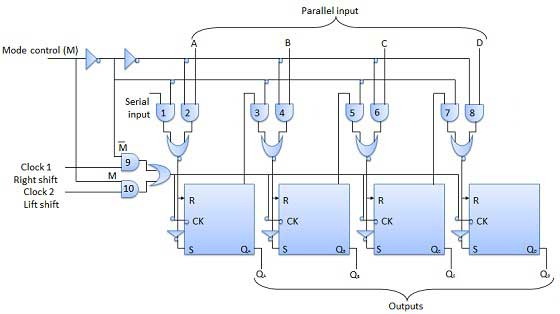
Đầu vào điều khiển chế độ được kết nối với logic 1 cho hoạt động tải song song trong khi nó được kết nối với 0 để chuyển dịch nối tiếp. Với chân điều khiển chế độ được kết nối với đất, thanh ghi dịch chuyển đa năng hoạt động như một thanh ghi hai chiều. Đối với hoạt động bên trái nối tiếp, đầu vào được áp dụng cho đầu vào nối tiếp đi đến cổng AND-1 được thể hiện trong hình. Trong khi đối với thao tác shift bên phải, đầu vào nối tiếp được áp dụng cho đầu vào D.
Sơ đồ khối
Bộ đếm là một mạch tuần tự. Một mạch kỹ thuật số được sử dụng để đếm xung được biết đến là bộ đếm. Bộ đếm là ứng dụng rộng nhất của dép xỏ ngón. Đó là một nhóm dép tông có áp dụng tín hiệu đồng hồ. Bộ đếm có hai loại.
- Bộ đếm không đồng bộ hoặc gợn sóng.
- Bộ đếm đồng bộ.
Bộ đếm không đồng bộ hoặc gợn sóng
Sơ đồ logic của bộ đếm gợn lên 2 bit được thể hiện trong hình. Bàn lật bật tắt (T) đang được sử dụng. Nhưng chúng ta có thể sử dụng flip-flop JK cũng với J và K được kết nối vĩnh viễn với logic 1. Xung nhịp ngoài được áp dụng cho đầu vào xung nhịp của flip-flop A và đầu ra Q A được áp dụng cho đầu vào xung nhịp của flip-flop tiếp theo tức là FF-B.
Sơ đồ lôgic
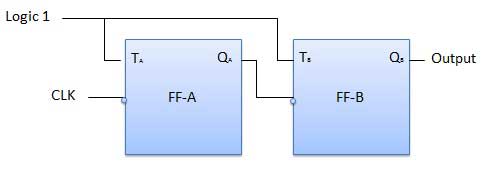
Hoạt động
| SN | Tình trạng | Hoạt động |
|---|---|---|
| 1 | Initially let both the FFs be in the reset state | Q B Q A = 00 ban đầu |
| 2 | After 1st negative clock edge | Ngay sau khi đặt cạnh xung nhịp âm đầu tiên, FF-A sẽ chuyển đổi và Q A sẽ bằng 1. Q A được kết nối với đầu vào xung nhịp của FF-B. Vì Q A đã thay đổi từ 0 thành 1, nó được coi là cạnh đồng hồ dương bởi FF-B. Không có sự thay đổi trong Q B vì FF-B là một cạnh âm được kích hoạt FF. Q B Q A = 01 sau xung clock đầu tiên. |
| 3 | After 2nd negative clock edge | Khi xuất hiện cạnh đồng hồ âm thứ hai, FF-A bật lại và Q A = 0. Sự thay đổi trong Q A hoạt động như một cạnh xung nhịp âm cho FF-B. Vì vậy, nó cũng sẽ chuyển đổi và Q B sẽ là 1. Q B Q A = 10 sau xung đồng hồ thứ hai. |
| 4 | After 3rd negative clock edge | Khi xuất hiện cạnh đồng hồ âm thứ 3, FF-A bật lại và Q A trở thành 1 từ 0. Vì đây là một thay đổi tích cực sẽ diễn ra, FF-B không phản ứng với nó và vẫn không hoạt động. Vậy Q B không đổi và tiếp tục bằng 1. Q B Q A = 11 sau xung clock thứ ba. |
| 5 | After 4th negative clock edge | Khi xuất hiện cạnh đồng hồ âm thứ 4, FF-A chuyển đổi một lần nữa và Q A trở thành 1 từ 0. Sự thay đổi âm này trong Q A hoạt động như xung đồng hồ cho FF-B. Do đó, nó chuyển đổi để thay đổi Q B từ 1 thành 0. Q B Q A = 00 sau xung clock thứ tư. |
Bảng sự thật
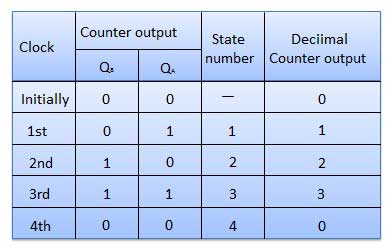
Bộ đếm đồng bộ
Nếu xung "đồng hồ" được áp dụng đồng thời cho tất cả các flip-flop trong bộ đếm, thì bộ đếm như vậy được gọi là bộ đếm đồng bộ.
Bộ đếm lên đồng bộ 2 bit
Các đầu vào J A và K A của FF-A được gắn với logic 1. Vì vậy, FF-A sẽ hoạt động như một flip-flop chuyển đổi. J B và K B đầu vào được kết nối với Q Một .
Sơ đồ lôgic

Hoạt động
| SN | Tình trạng | Hoạt động |
|---|---|---|
| 1 | Initially let both the FFs be in the reset state | Q B Q A = 00 ban đầu. |
| 2 | After 1st negative clock edge | Ngay khi áp dụng cạnh đồng hồ âm đầu tiên, FF-A sẽ chuyển đổi và Q A sẽ thay đổi từ 0 thành 1. Nhưng tại thời điểm áp dụng cạnh đồng hồ âm, Q A , J B = K B = 0. Do đó FF-B sẽ không thay đổi trạng thái của nó. Vì vậy Q B sẽ vẫn là 0. Q B Q A = 01 sau xung clock đầu tiên. |
| 3 | After 2nd negative clock edge | Khi xuất hiện cạnh đồng hồ âm thứ hai, FF-A lại bật tắt và Q A thay đổi từ 1 thành 0. Nhưng tại thời điểm này Q A là 1. Vì vậy, J B = K B = 1 và FF-B sẽ chuyển đổi. Do đó Q B thay đổi từ 0 thành 1. Q B Q A = 10 sau xung đồng hồ thứ hai. |
| 4 | After 3rd negative clock edge | Khi áp dụng cạnh đồng hồ rơi thứ ba, FF-A sẽ chuyển từ 0 thành 1 nhưng không có sự thay đổi trạng thái nào đối với FF-B. Q B Q A = 11 sau xung clock thứ ba. |
| 5 | After 4th negative clock edge | Khi áp dụng xung đồng hồ tiếp theo, Q A sẽ thay đổi từ 1 thành 0 và Q B cũng sẽ thay đổi từ 1 thành 0. Q B Q A = 00 sau xung clock thứ tư. |
Phân loại quầy
Tùy thuộc vào cách mà tiến trình đếm, bộ đếm đồng bộ hoặc không đồng bộ được phân loại như sau:
- Lên quầy
- Quầy xuống
- Quầy lên / xuống
Bộ đếm LÊN / XUỐNG
Bộ đếm lên và bộ đếm xuống được kết hợp với nhau để có được bộ đếm LÊN / XUỐNG. Một đầu vào điều khiển chế độ (M) cũng được cung cấp để chọn chế độ lên hoặc xuống. Một mạch tổ hợp được yêu cầu phải được thiết kế và sử dụng giữa mỗi cặp flip-flop để đạt được hoạt động lên / xuống.
- Loại bộ đếm lên / xuống
- Bộ đếm gợn sóng LÊN / XUỐNG
- Bộ đếm đồng bộ LÊN / XUỐNG
Bộ đếm Ripple LÊN / XUỐNG
Trong bộ đếm gợn sóng LÊN / XUỐNG tất cả các FF hoạt động ở chế độ bật tắt. Vì vậy, dép xỏ ngón T hoặc dép xỏ ngón JK sẽ được sử dụng. LSB flip-flop nhận đồng hồ trực tiếp. Nhưng xung nhịp cho mọi FF khác được lấy từ đầu ra (Q = Q bar) của FF trước đó.
UP counting mode (M=0)- Đầu ra Q của FF trước được kết nối với đồng hồ của giai đoạn tiếp theo nếu muốn đạt được đếm tăng. Đối với chế độ này, đầu vào chọn chế độ M ở mức logic 0 (M = 0).
DOWN counting mode (M=1)- Nếu M = 1 thì ngõ ra thanh Q của FF trước được nối với FF sau. Thao tác này sẽ vận hành bộ đếm ở chế độ đếm.
Thí dụ
Bộ đếm gợn sóng lên / xuống nhị phân 3 bit.
3-bit - do đó cần có ba FF.
LÊN / XUỐNG - Vì vậy, một đầu vào điều khiển chế độ là cần thiết.
Đối với bộ đếm gợn sóng, đầu ra Q của FF trước được kết nối với đầu vào xung nhịp của FF tiếp theo.
Đối với bộ đếm gợn sóng, đầu ra Q của FF trước được kết nối với đầu vào xung nhịp của FF tiếp theo.
Đối với bộ đếm gợn sóng xuống, đầu ra thanh Q của FF trước được kết nối với đầu vào xung nhịp của FF tiếp theo.
Để việc lựa chọn đầu ra thanh Q và Q của FF trước được điều khiển bởi đầu vào điều khiển chế độ M sao cho, Nếu M = 0, đếm TĂNG. Vì vậy, kết nối Q với CLK. Nếu M = 1, đếm XUỐNG. Vì vậy, kết nối thanh Q với CLK.
Sơ đồ khối
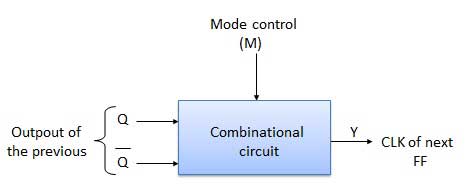
Bảng sự thật
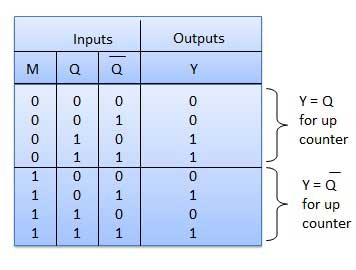
Hoạt động
| SN | Tình trạng | Hoạt động |
|---|---|---|
| 1 | Case 1 − With M = 0 (Up counting mode) | Nếu M = 0 và M bar = 1, thì cổng AND 1 và 3 trong hình. sẽ được kích hoạt trong khi cổng AND 2 và 4 sẽ bị tắt. Do đó Q A được kết nối với đầu vào xung nhịp của FF-B và Q B được kết nối với đầu vào xung nhịp của FF-C. Các kết nối này giống như kết nối của bộ đếm tăng thông thường. Do đó với M = 0 mạch hoạt động như một bộ đếm tăng. |
| 2 | Case 2: With M = 1 (Down counting mode) | Nếu M = 1, thì cổng AND 2 và 4 trong hình. được bật trong khi cổng AND 1 và 3 bị tắt. Do đó thanh Q A được kết nối với đầu vào xung nhịp của FF-B và thanh Q B được kết nối với đầu vào xung nhịp của FF-C. Các kết nối này sẽ tạo ra một bộ đếm giảm. Như vậy với M = 1 mạch hoạt động như một bộ đếm giảm. |
Bộ đếm mô-đun (Bộ đếm MOD-N)
Bộ đếm gợn sóng 2 bit được gọi là bộ đếm MOD-4 và bộ đếm độ gợn sóng 3 bit được gọi là bộ đếm MOD-8. Vì vậy, nói chung, một bộ đếm gợn sóng n bit được gọi là bộ đếm modulo-N. Trong đó, số MOD = 2 n .
Loại mô đun
- 2-bit lên hoặc xuống (MOD-4)
- 3-bit lên hoặc xuống (MOD-8)
- 4-bit lên hoặc xuống (MOD-16)
Ứng dụng của quầy
- Bộ đếm tần số
- Đồng hồ kỹ thuật số
- Đo thời gian
- Công cụ chuyển đổi A sang D
- Mạch phân tần
- Bộ tạo sóng tam giác kỹ thuật số.
Trí nhớ cũng giống như bộ não con người. Nó được sử dụng để lưu trữ dữ liệu và hướng dẫn. Bộ nhớ máy tính là không gian lưu trữ trong máy tính, nơi dữ liệu được xử lý và lưu trữ các hướng dẫn cần thiết để xử lý.
Bộ nhớ được chia thành nhiều phần nhỏ. Mỗi phần được gọi là một ô. Mỗi vị trí hoặc ô có một địa chỉ duy nhất thay đổi từ 0 đến kích thước bộ nhớ trừ đi một.
Ví dụ: nếu máy tính có 64k từ, thì đơn vị bộ nhớ này có vị trí bộ nhớ 64 * 1024 = 65536. Địa chỉ của các địa điểm này thay đổi từ 0 đến 65535.
Bộ nhớ chủ yếu có hai loại
Internal Memory - bộ nhớ đệm và bộ nhớ chính / chính
External Memory - đĩa từ / đĩa quang, v.v.
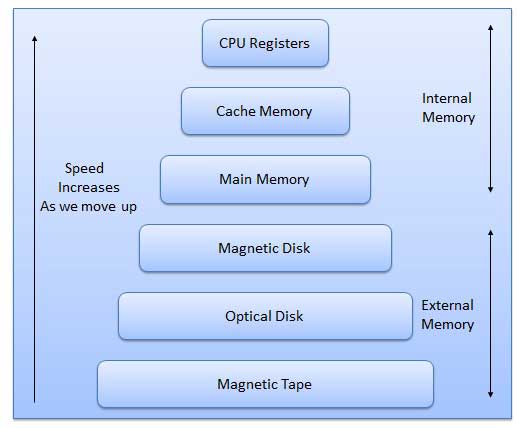
Đặc điểm của Hệ thống phân cấp bộ nhớ là theo sau khi chúng ta đi từ trên xuống dưới.
- Khả năng lưu trữ tăng lên.
- Giá mỗi bit lưu trữ giảm.
- Tần suất truy cập bộ nhớ của CPU giảm.
- Thời gian truy cập của CPU tăng lên.
RAM
RAM cấu thành bộ nhớ trong của CPU để lưu trữ dữ liệu, chương trình và kết quả của chương trình. Nó là bộ nhớ đọc / ghi. Nó được gọi là bộ nhớ truy cập ngẫu nhiên (RAM).
Vì thời gian truy cập trong RAM không phụ thuộc vào địa chỉ của từ đó, nên mỗi vị trí lưu trữ bên trong bộ nhớ dễ dàng truy cập như vị trí khác & mất cùng một khoảng thời gian. Chúng ta có thể truy cập vào bộ nhớ một cách ngẫu nhiên và cực kỳ nhanh chóng nhưng cũng có thể khá tốn kém.
RAM dễ bay hơi, tức là dữ liệu lưu trữ trong đó bị mất khi chúng ta tắt máy tính hoặc khi mất điện. Do đó, hệ thống điện liên tục dự phòng (UPS) thường được sử dụng với máy tính. RAM nhỏ, cả về kích thước vật lý và lượng dữ liệu mà nó có thể chứa.
RAM có hai loại
- RAM tĩnh (SRAM)
- RAM động (DRAM)
RAM tĩnh (SRAM)
Từ staticchỉ ra rằng bộ nhớ vẫn giữ nội dung của nó miễn là vẫn còn nguồn. Tuy nhiên, dữ liệu bị mất khi mất điện do tính chất dễ bay hơi. Các chip SRAM sử dụng ma trận gồm 6 bóng bán dẫn và không có tụ điện. Các bóng bán dẫn không yêu cầu nguồn điện để ngăn rò rỉ, vì vậy SRAM không cần phải được làm mới thường xuyên.
Do có thêm không gian trong ma trận, SRAM sử dụng nhiều chip hơn DRAM cho cùng một lượng không gian lưu trữ, do đó làm cho chi phí sản xuất cao hơn.
RAM tĩnh được sử dụng làm bộ nhớ đệm cần rất nhanh và nhỏ.
RAM động (DRAM)
DRAM, không giống như SRAM, phải liên tục refreshedđể nó duy trì dữ liệu. Điều này được thực hiện bằng cách đặt bộ nhớ trên một mạch làm mới ghi lại dữ liệu vài trăm lần mỗi giây. DRAM được sử dụng cho hầu hết bộ nhớ hệ thống vì nó rẻ và nhỏ. Tất cả các DRAM đều được tạo thành từ các ô nhớ. Các tế bào này bao gồm một tụ điện và một bóng bán dẫn.
ROM
ROM là viết tắt của Read Only Memory. Bộ nhớ mà từ đó chúng ta chỉ có thể đọc nhưng không thể ghi trên đó. Đây là loại bộ nhớ không thay đổi. Thông tin được lưu trữ vĩnh viễn trong ký ức như vậy trong quá trình sản xuất.
Một ROM, lưu trữ các chỉ dẫn như được yêu cầu để khởi động máy tính khi bật điện lần đầu tiên, thao tác này được gọi là bootstrap. Chip ROM không chỉ được sử dụng trong máy tính mà còn trong các thiết bị điện tử khác như máy giặt và lò vi sóng.
Sau đây là các loại ROM khác nhau -
MROM (ROM có mặt nạ)
Những bản ROM đầu tiên là những thiết bị có dây cứng chứa một bộ dữ liệu hoặc hướng dẫn được lập trình sẵn. Những loại ROM này được gọi là ROM bị che. Nó là ROM rẻ tiền.
PROM (Bộ nhớ chỉ đọc có thể lập trình)
PROM là bộ nhớ chỉ đọc, người dùng chỉ có thể sửa đổi một lần. Người dùng mua một PROM trống và nhập nội dung mong muốn bằng cách sử dụng một lập trình viên PROM. Bên trong chip PROM có các cầu chì nhỏ bị cháy mở trong quá trình lập trình. Nó chỉ có thể được lập trình một lần và không thể xóa được.
EPROM (Bộ nhớ chỉ đọc có thể xóa và có thể lập trình)
EPROM có thể bị xóa bằng cách cho nó tiếp xúc với ánh sáng cực tím trong thời gian tối đa 40 phút. Thông thường, một công cụ xóa EPROM đạt được chức năng này. Trong quá trình lập trình, điện tích bị kẹt trong vùng cổng cách điện. Cước được giữ lại hơn mười năm vì cước không có đường rò. Để xóa điện tích này, ánh sáng cực tím được truyền qua cửa sổ tinh thể thạch anh (nắp). Việc tiếp xúc với ánh sáng cực tím này sẽ làm tiêu hao điện tích. Trong quá trình sử dụng bình thường, nắp thạch anh được niêm phong bằng nhãn dán.
EEPROM (Bộ nhớ chỉ đọc có thể xóa bằng điện và có thể lập trình)
EEPROM được lập trình và xóa bằng điện. Nó có thể được xóa và lập trình lại khoảng mười nghìn lần. Cả quá trình xóa và lập trình mất khoảng 4 đến 10 mili giây (mili giây). Trong EEPROM, bất kỳ vị trí nào cũng có thể được xóa và lập trình có chọn lọc. Các EEPROM có thể được xóa từng byte một, thay vì xóa toàn bộ chip. Do đó, quá trình lập trình lại linh hoạt nhưng chậm.
Bộ nhớ truy cập nối tiếp
Truy cập tuần tự có nghĩa là hệ thống phải tìm kiếm thiết bị lưu trữ từ đầu địa chỉ bộ nhớ cho đến khi tìm thấy phần dữ liệu cần thiết. Thiết bị nhớ hỗ trợ truy cập như vậy được gọi là Bộ nhớ truy cập tuần tự hoặc Bộ nhớ truy cập nối tiếp. Băng từ là một ví dụ về bộ nhớ truy cập nối tiếp.
Bộ nhớ truy cập trực tiếp
Bộ nhớ truy cập trực tiếp hoặc Bộ nhớ truy cập ngẫu nhiên, đề cập đến các điều kiện trong đó hệ thống có thể truy cập trực tiếp đến thông tin mà người dùng muốn. Thiết bị nhớ hỗ trợ truy cập như vậy được gọi là Bộ nhớ truy cập trực tiếp. Đĩa từ, đĩa quang là những ví dụ về bộ nhớ truy cập trực tiếp.
Bộ nhớ đệm
Bộ nhớ đệm là bộ nhớ bán dẫn tốc độ rất cao có thể tăng tốc CPU. Nó hoạt động như một bộ đệm giữa CPU và bộ nhớ chính. Nó được sử dụng để giữ những phần dữ liệu và chương trình được CPU sử dụng thường xuyên nhất. Các phần dữ liệu và chương trình được hệ điều hành chuyển từ đĩa sang bộ nhớ đệm, từ đó CPU có thể truy cập chúng.
Ưu điểm
- Bộ nhớ đệm nhanh hơn bộ nhớ chính.
- Nó tiêu tốn ít thời gian truy cập hơn so với bộ nhớ chính.
- Nó lưu trữ chương trình có thể được thực thi trong một khoảng thời gian ngắn.
- Nó lưu trữ dữ liệu để sử dụng tạm thời.
Nhược điểm
- Bộ nhớ đệm có dung lượng hạn chế.
- Nó rất đắt.
Bộ nhớ ảo là một kỹ thuật cho phép thực hiện các quá trình không hoàn toàn có sẵn trong bộ nhớ. Ưu điểm chính có thể nhìn thấy của lược đồ này là các chương trình có thể lớn hơn bộ nhớ vật lý. Bộ nhớ ảo là sự tách biệt bộ nhớ logic của người dùng khỏi bộ nhớ vật lý.
Sự tách biệt này cho phép cung cấp một bộ nhớ ảo cực lớn cho các lập trình viên khi chỉ có một bộ nhớ vật lý nhỏ hơn. Sau đây là các tình huống, khi toàn bộ chương trình không được yêu cầu tải đầy đủ vào bộ nhớ chính.
Quy trình xử lý lỗi do người dùng viết chỉ được sử dụng khi xảy ra lỗi trong dữ liệu hoặc tính toán.
Một số tùy chọn và tính năng của chương trình có thể hiếm khi được sử dụng.
Nhiều bảng được chỉ định một lượng không gian địa chỉ cố định mặc dù chỉ có một lượng nhỏ bảng được sử dụng thực sự.
Khả năng thực thi một chương trình chỉ có một phần trong bộ nhớ sẽ phản lại nhiều lợi ích.
Số lượng I / O ít hơn sẽ cần thiết để tải hoặc hoán đổi từng chương trình người dùng vào bộ nhớ.
Một chương trình sẽ không còn bị giới hạn bởi dung lượng bộ nhớ vật lý có sẵn.
Mỗi chương trình người dùng có thể chiếm ít bộ nhớ vật lý hơn, nhiều chương trình hơn có thể được chạy cùng một lúc, với sự gia tăng tương ứng trong việc sử dụng và thông lượng CPU.
Bộ nhớ phụ
Bộ nhớ phụ có kích thước lớn hơn nhiều so với bộ nhớ chính nhưng tốc độ chậm hơn. Nó thường lưu trữ các chương trình hệ thống, các tệp hướng dẫn và dữ liệu. Nó còn được gọi là bộ nhớ phụ. Nó cũng có thể được sử dụng như một bộ nhớ tràn / bộ nhớ ảo trong trường hợp dung lượng bộ nhớ chính đã bị vượt quá. Bộ xử lý không thể truy cập trực tiếp các bộ nhớ thứ cấp. Đầu tiên dữ liệu / thông tin của bộ nhớ phụ được chuyển đến bộ nhớ chính và sau đó thông tin đó có thể được truy cập bởi CPU. Các đặc điểm của bộ nhớ phụ như sau:
Non-volatile memory - Dữ liệu không bị mất khi cúp điện.
Reusable - Dữ liệu vẫn ở trong bộ nhớ thứ cấp trên cơ sở vĩnh viễn cho đến khi nó không bị người dùng ghi đè hoặc xóa.
Reliable - Dữ liệu trong bộ lưu trữ thứ cấp an toàn vì tính ổn định vật lý cao của thiết bị lưu trữ thứ cấp.
Convenience - Với sự trợ giúp của phần mềm máy tính, những người có thẩm quyền có thể xác định vị trí và truy cập dữ liệu một cách nhanh chóng.
Capacity - Bộ nhớ thứ cấp có thể lưu trữ khối lượng lớn dữ liệu trong bộ nhiều đĩa.
Cost - Lưu trữ dữ liệu trên băng hoặc đĩa rẻ hơn nhiều so với bộ nhớ chính.
Khối vi xử lý đồng nghĩa với khối xử lý trung tâm, CPU được sử dụng trong máy tính truyền thống. Bộ vi xử lý (MPU) hoạt động như một thiết bị hoặc một nhóm thiết bị thực hiện các tác vụ sau.
- giao tiếp với các thiết bị ngoại vi
- cung cấp tín hiệu thời gian
- luồng dữ liệu trực tiếp
- thực hiện các tác vụ máy tính theo chỉ dẫn trong bộ nhớ
Bộ vi xử lý 8085
Bộ vi xử lý 8085 là một bộ vi xử lý đa năng 8 bit có khả năng xử lý 64k bộ nhớ. Bộ xử lý này có bốn mươi chân, yêu cầu nguồn điện đơn +5 V và xung nhịp một pha 3 MHz.
Sơ đồ khối
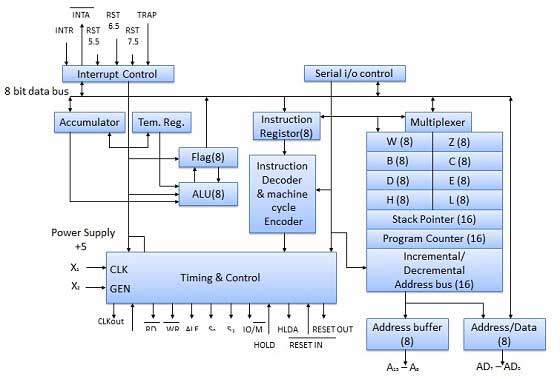
ALU
ALU thực hiện chức năng tính toán của bộ vi xử lý. Nó bao gồm bộ tích lũy, thanh ghi tạm thời, mạch số học & logic & và năm cờ. Kết quả được lưu trữ trong bộ tích lũy và cờ.
Sơ đồ khối

Tích lũy
Nó là một thanh ghi 8-bit là một phần của ALU. Thanh ghi này được sử dụng để lưu trữ dữ liệu 8 bit và thực hiện phép toán số học & logic. Kết quả của hoạt động được lưu trữ trong bộ tích lũy.
Biểu đồ
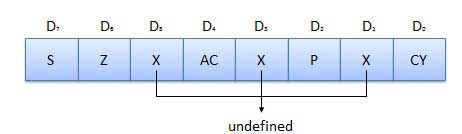
Cờ
Cờ có thể lập trình được. Chúng có thể được sử dụng để lưu trữ và chuyển dữ liệu từ các thanh ghi bằng cách sử dụng lệnh. ALU bao gồm năm flip-flops được đặt và đặt lại theo tình trạng dữ liệu trong bộ tích lũy và các thanh ghi khác.
S (Sign) flag- Sau khi thực hiện một phép tính số học, nếu bit D 7 của kết quả là 1 thì cờ dấu được đặt. Nó được sử dụng để ký số. Trong một byte nhất định, nếu D 7 là 1 có nghĩa là số âm. Nếu nó là số 0 có nghĩa là nó là một số dương.
Z (Zero) flag - Cờ số không được đặt nếu kết quả hoạt động ALU là 0.
AC (Auxiliary Carry) flag- Trong phép toán số học, khi carry được tạo bởi chữ số D3 và chuyển cho chữ số D 4 , cờ AC được thiết lập. Cờ này chỉ được sử dụng trong hoạt động BCD nội bộ.
P (Parity) flag- Sau phép toán số học hoặc logic, nếu kết quả có số chẵn là 1 thì cờ được đặt. Nếu nó có số lẻ là 1, cờ được đặt lại.
C (Carry) flag - Nếu kết quả hoạt động số học là một dấu hiệu, cờ mang được đặt, nếu không, nó sẽ được đặt lại.
Đăng ký phần
Về cơ bản nó là một thiết bị lưu trữ và chuyển dữ liệu từ các thanh ghi bằng cách sử dụng các hướng dẫn.
Stack Pointer (SP)- Con trỏ ngăn xếp cũng là một thanh ghi 16 bit được sử dụng như một con trỏ bộ nhớ. Nó trỏ đến một vị trí bộ nhớ trong bộ nhớ Đọc / Ghi được gọi là ngăn xếp. Giữa quá trình thực thi chương trình, đôi khi dữ liệu sẽ được lưu trữ trong ngăn xếp. Sự bắt đầu của ngăn xếp được xác định bằng cách tải một địa chỉ 16 bit trong con trỏ ngăn xếp.
Program Counter (PC)- Thanh ghi 16-bit này xử lý hoạt động thứ tư để trình tự thực hiện lệnh. Thanh ghi này cũng là một con trỏ bộ nhớ. Vị trí bộ nhớ có địa chỉ 16-bit. Nó được sử dụng để lưu trữ địa chỉ thực thi. Chức năng của bộ đếm chương trình là trỏ đến địa chỉ bộ nhớ mà byte tiếp theo sẽ được tìm nạp.
Storage registers- Các thanh ghi này lưu trữ dữ liệu 8 bit trong quá trình thực hiện chương trình. Các thanh ghi này được xác định là B, C, D, E, H, L. Chúng có thể được kết hợp thành cặp thanh ghi BC, DE và HL để thực hiện một số hoạt động 16 bit.
Phần kiểm soát và thời gian
Bộ phận này có nhiệm vụ đồng bộ hóa hoạt động của Bộ vi xử lý theo xung đồng hồ và tạo ra các tín hiệu điều khiển cần thiết để giao tiếp thông suốt giữa Bộ vi xử lý và các thiết bị ngoại vi. Các tín hiệu thanh RD và thanh WR là các xung đồng bộ cho biết dữ liệu có sẵn trên bus dữ liệu hay không. Khối điều khiển có nhiệm vụ điều khiển luồng dữ liệu giữa bộ vi xử lý, bộ nhớ và các thiết bị ngoại vi.
Sơ đồ mã PIN

Tất cả các tín hiệu có thể được phân loại thành sáu nhóm
| SN | Nhóm | Sự miêu tả |
|---|---|---|
| 1 | Address bus | Bộ vi xử lý 8085 có 8 đường tín hiệu, A 15 - A 8 là một hướng và được sử dụng như một bus địa chỉ bậc cao. |
| 2 | Data bus | Đường tín hiệu AD7 - AD0 là hai hướng cho mục đích kép. Chúng được sử dụng làm bus địa chỉ thứ tự thấp cũng như bus dữ liệu. |
| 3 | Control signal and Status signal | Tín hiệu điều khiển RD bar- Nó là một tín hiệu điều khiển đọc (hoạt động thấp). Nếu nó đang hoạt động thì bộ nhớ sẽ đọc dữ liệu. WR bar- Đó là tín hiệu điều khiển ghi (hoạt động ở mức thấp). Nó hoạt động khi được ghi vào bộ nhớ đã chọn. Tín hiệu trạng thái ALU (Address Latch Enable)- Khi ALU cao. Bộ vi xử lý 8085 sử dụng bus địa chỉ. Khi ALU thấp. Bộ vi xử lý 8085 được sử dụng bus dữ liệu. IO/M bar- Đây là một tín hiệu trạng thái được sử dụng để phân biệt giữa i / o và các hoạt động bộ nhớ. Khi ở mức cao, nó cho biết hoạt động i / o và khi ở mức thấp, nó cho biết hoạt động của bộ nhớ. S1 and S0 - Các tín hiệu trạng thái này, tương tự như i / o và thanh bộ nhớ, có thể xác định các hoạt động khác nhau, nhưng chúng hiếm khi được sử dụng trong hệ thống nhỏ. |
| 4 | Power supply and frequency signal | Vcc - + Nguồn điện 5v. Vss - tham chiếu mặt bằng. X, X- Một viên pha lê được nối ở hai chốt này. Tần số được phân chia bên trong cho hai hệ thống hoạt động là 3 MHz, tinh thể phải có tần số 6 MHz. CLK out - Tín hiệu này có thể được sử dụng làm đồng hồ hệ thống cho các thiết bị khác. |
| 5 | Externally initiated signal | INTR (i/p) - Yêu cầu ngắt. INTA bar (o/p) - Nó được sử dụng như ngắt xác nhận. TRAP (i/p) - Đây là ngắt không che được và có mức ưu tiên cao nhất. HOLD (i/p) - Nó dùng để chứa chương trình đang thực thi. HLDA (o/p) - Giữ xác nhận. READY (i/p) - Tín hiệu này được sử dụng để trì hoãn chu kỳ đọc hoặc ghi của bộ vi xử lý cho đến khi một thiết bị ngoại vi phản hồi chậm sẵn sàng chấp nhận hoặc gửi dữ liệu. RESET IN bar - Khi tín hiệu trên chân này ở mức thấp, bộ đếm chương trình được đặt thành 0, bus được xác định ba lần, & MPU được đặt lại. RESET OUT- Tín hiệu này cho biết MPU đang được thiết lập lại. Tín hiệu có thể được sử dụng để thiết lập lại các thiết bị khác. RST 7.5, RST 6.5, RST 5.5 (Request interrupt)- Nó được sử dụng để chuyển điều khiển chương trình đến vị trí bộ nhớ cụ thể. Chúng có mức ưu tiên cao hơn ngắt INTR. |
| 6 | Serial I/O ports | Bộ vi xử lý 8085 có hai tín hiệu để thực hiện dữ liệu đầu vào nối tiếp truyền nối tiếp và dữ liệu đầu ra nối tiếp. |
Định dạng hướng dẫn
Mỗi lệnh được biểu diễn bằng một chuỗi các bit trong máy tính. Lệnh được chia thành nhóm bit được gọi là trường. Cách thể hiện hướng dẫn được gọi là định dạng lệnh. Nó thường được biểu diễn dưới dạng hình hộp chữ nhật. Định dạng hướng dẫn có thể thuộc các loại sau.
Định dạng lệnh biến
Đây là các định dạng lệnh trong đó độ dài lệnh thay đổi trên cơ sở các chỉ định opcode & địa chỉ. Ví dụ, lệnh VAX thay đổi từ 1 đến 53 byte trong khi lệnh X86 thay đổi từ 1 đến 17 byte.
định dạng

Lợi thế
Các định dạng này có mật độ mã tốt.
Hạn chế
Các định dạng lệnh này rất khó giải mã và chuyển hướng.
Định dạng hướng dẫn cố định
Trong loại định dạng hướng dẫn này, tất cả các lệnh đều có cùng kích thước. Ví dụ, MIPS, Power PC, Alpha, ARM.
định dạng

Lợi thế
Chúng dễ dàng để giải mã và đường ống.
Hạn chế
Chúng không có mật độ mã tốt.
Định dạng hướng dẫn kết hợp
Trong loại định dạng hướng dẫn này, chúng tôi có nhiều độ dài định dạng được chỉ định bởi opcode. Ví dụ: IBM 360/70, MIPS 16, Ngón tay cái.
định dạng

Lợi thế
Sự thỏa hiệp giữa mật độ mã và hướng dẫn của loại này rất dễ giải mã.
Chế độ địa chỉ
Chế độ định địa chỉ cung cấp các cách khác nhau để truy cập địa chỉ tới dữ liệu đã cho tới bộ xử lý. Dữ liệu đã vận hành được lưu trong vị trí bộ nhớ, mỗi lệnh yêu cầu dữ liệu nhất định mà nó phải hoạt động. Có nhiều kỹ thuật khác nhau để xác định địa chỉ của dữ liệu. Các kỹ thuật này được gọi là Chế độ định địa chỉ.
Direct addressing mode- Trong chế độ định địa chỉ trực tiếp, địa chỉ của toán hạng được đưa ra trong lệnh và dữ liệu có sẵn trong vị trí bộ nhớ được cung cấp trong lệnh. Chúng tôi sẽ di chuyển dữ liệu này đến vị trí mong muốn.
Indirect addressing mode- Trong chế độ định địa chỉ gián tiếp, lệnh chỉ định một thanh ghi chứa địa chỉ của toán hạng. Cả RAM trong và RAM ngoài đều có thể được truy cập thông qua chế độ định địa chỉ gián tiếp.
Immediate addressing mode- Trong chế độ định địa chỉ tức thời, dữ liệu trực tiếp được đưa ra trong toán hạng sẽ di chuyển dữ liệu trong bộ tích lũy. Nó rất nhanh.
Relative addressing mode- Trong chế độ địa chỉ tương đối, địa chỉ hiệu dụng được xác định bởi chế độ chỉ mục bằng cách sử dụng bộ đếm chương trình thay cho thanh ghi bộ xử lý mục đích chung. Chế độ này được gọi là chế độ địa chỉ tương đối.
Index addressing mode- Trong chế độ địa chỉ chỉ mục, địa chỉ hiệu dụng của toán hạng được tạo ra bằng cách thêm một giá trị nội dung vào nội dung của thanh ghi. Chế độ này được gọi là chế độ địa chỉ chỉ mục.