Toán học rời rạc - Lý thuyết nhóm

Semigroup

Một tập hợp hữu hạn hoặc vô hạn $ 'S' $ với phép toán nhị phân $ '\ omicron' $ (Thành phần) được gọi là semigroup nếu nó đồng thời tuân theo hai điều kiện sau:

Closure - Với mọi cặp $ (a, b) \ in S, \ :( a \ omicron b) $ phải có trong tập $ S $.
Associative - Với mọi phần tử $ a, b, c \ trong S, (a \ omicron b) \ omicron c = a \ omicron (b \ omicron c) $ phải giữ.

Thí dụ

Tập hợp các số nguyên dương (không bao gồm số 0) với phép toán cộng là một nhóm bán nghĩa. Ví dụ: $ S = \ lbrace 1, 2, 3, \ dot \ rbrace $

Ở đây thuộc tính đóng giữ như đối với mọi cặp $ (a, b) \ trong S, (a + b) $ có trong tập S. Ví dụ, $ 1 + 2 = 3 \ in S] $

Thuộc tính liên kết cũng giữ cho mọi phần tử $ a, b, c \ trong S, (a + b) + c = a + (b + c) $. Ví dụ: $ (1 + 2) + 3 = 1 + (2 + 3) = 5 $

Monoid

Một monoid là một nửa nhóm với một phần tử nhận dạng. Phần tử đồng nhất (ký hiệu là $ e $ hoặc E) của tập S là phần tử sao cho $ (a \ omicron e) = a $, với mọi phần tử $ a \ trong S $. Yếu tố nhận dạng còn được gọi làunit element. Vì vậy, một monoid có ba thuộc tính đồng thời -Closure, Associative, Identity element.

Thí dụ

Tập hợp các số nguyên dương (không bao gồm số 0) với phép nhân là một đơn nguyên. $ S = \ lbrace 1, 2, 3, \ dot \ rbrace $

Ở đây thuộc tính đóng giữ như mọi cặp $ (a, b) \ trong S, (a \ times b) $ có trong tập S. [Ví dụ: $ 1 \ times 2 = 2 \ in S $, v.v.]

Thuộc tính liên kết cũng giữ cho mọi phần tử $ a, b, c \ trong S, (a \ times b) \ times c = a \ times (b \ times c) $ [Ví dụ: $ (1 \ times 2) \ times 3 = 1 \ lần (2 \ lần 3) = 6 $, v.v.]

Thuộc tính danh tính cũng giữ cho mọi phần tử $ a \ trong S, (a \ times e) = a $ [Ví dụ: $ (2 \ times 1) = 2, (3 \ times 1) = 3 $, v.v.]. Ở đây yếu tố nhận dạng là 1.

Nhóm

Một nhóm là một đơn nguyên với một phần tử nghịch đảo. Phần tử nghịch đảo (ký hiệu là I) của tập S là phần tử sao cho $ (a \ omicron I) = (I \ omicron a) = a $, với mỗi phần tử $ a \ trong S $. Vì vậy, một nhóm có bốn thuộc tính đồng thời - i) Đóng, ii) Liên kết, iii) Yếu tố nhận dạng, iv) Yếu tố nghịch đảo. Bậc của một nhóm G là số phần tử trong G và bậc của một phần tử trong một nhóm là số nguyên dương n nhỏ nhất sao cho an là phần tử đồng nhất của nhóm G đó.

Ví dụ

Tập hợp $ N \ times N $ ma trận không số ít tạo thành một nhóm trong phép toán nhân ma trận.

Tích của hai ma trận không số ít $ N \ times N $ cũng là một ma trận không số ít $ N \ times N $ chứa thuộc tính đóng.

Phép nhân ma trận chính nó là liên kết. Do đó, tài sản liên kết được giữ.

Tập hợp $ N \ times N $ ma trận không số ít chứa ma trận nhận dạng chứa thuộc tính phần tử nhận dạng.

Vì tất cả các ma trận đều không phải là số ít nên tất cả đều có các phần tử nghịch đảo cũng là ma trận không số ít. Do đó, tài sản nghịch đảo cũng được giữ.

Nhóm Abelian

Nhóm abelian G là nhóm mà cặp phần tử $ (a, b) \ trong G $ luôn giữ luật giao hoán. Vì vậy, một nhóm nắm giữ đồng thời năm thuộc tính - i) Đóng, ii) Liên kết, iii) Yếu tố nhận dạng, iv) Yếu tố nghịch đảo, v) Giao hoán.

Thí dụ

Tập hợp các số nguyên dương (bao gồm cả số 0) với phép toán cộng là một nhóm abel. $ G = \ lbrace 0, 1, 2, 3, \ dot \ rbrace $

Ở đây thuộc tính đóng giữ như đối với mọi cặp $ (a, b) \ trong S, (a + b) $ có trong tập S. [Ví dụ: $ 1 + 2 = 2 \ in S $, v.v.]

Thuộc tính liên kết cũng giữ cho mọi phần tử $ a, b, c \ trong S, (a + b) + c = a + (b + c) $ [Ví dụ: $ (1 +2) + 3 = 1 + (2 + 3) = 6 $, v.v.]

Thuộc tính danh tính cũng giữ cho mọi phần tử $ a \ trong S, (a \ times e) = a $ [Ví dụ: $ (2 \ times 1) = 2, (3 \ times 1) = 3 $, v.v.]. Ở đây, yếu tố nhận dạng là 1.

Thuộc tính giao hoán cũng giữ cho mọi phần tử $ a \ trong S, (a \ times b) = (b \ times a) $ [Ví dụ: $ (2 \ times 3) = (3 \ times 2) = 3 $ và tương tự trên]

Nhóm tuần hoàn và nhóm con

A cyclic grouplà một nhóm có thể được tạo bởi một phần tử duy nhất. Mỗi phần tử của một nhóm tuần hoàn là công suất của một phần tử cụ thể nào đó được gọi là máy phát. Một nhóm tuần hoàn có thể được tạo ra bởi bộ tạo 'g', sao cho mọi phần tử khác của nhóm có thể được viết dưới dạng công suất của bộ tạo 'g'.

Thí dụ

Tập hợp các số phức $ \ lbrace 1, -1, i, -i \ rbrace $ trong phép toán nhân là một nhóm tuần hoàn.

Có hai trình tạo - $ i $ và $ –i $ là $ i ^ 1 = i, i ^ 2 = -1, i ^ 3 = -i, i ^ 4 = 1 $ và cả $ (- i) ^ 1 = -i, (–i) ^ 2 = -1, (–i) ^ 3 = i, (–i) ^ 4 = 1 $ bao gồm tất cả các phần tử của nhóm. Do đó, nó là một nhóm tuần hoàn.

Note - A cyclic groupluôn là nhóm abel nhưng không phải mọi nhóm abel đều là nhóm tuần hoàn. Các số hữu tỉ trong phép cộng không phải là chu kỳ mà là số abel.

A subgroup H là một tập con của nhóm G (ký hiệu là $ H ≤ G $) nếu nó thỏa mãn đồng thời bốn thuộc tính: Closure, Associative, Identity elementvà Inverse.

Nhóm con H của nhóm G mà không bao gồm toàn bộ nhóm G được gọi là nhóm con thích hợp (Ký hiệu là $ H <G $). Một nhóm con của một nhóm cyclic là tuần hoàn và một nhóm con abelian cũng là abelian.

Thí dụ

Cho nhóm $ G = \ lbrace 1, i, -1, -i \ rbrace $

Sau đó, một số nhóm con là $ H_1 = \ lbrace 1 \ rbrace, H_2 = \ lbrace 1, -1 \ rbrace $,

Đây không phải là một nhóm con - $ H_3 = \ lbrace 1, tôi \ rbrace $ vì $ (i) ^ {- 1} = -i $ không thuộc $ H_3 $

Bộ được đặt hàng một phần (POSET)

Một tập hợp có thứ tự một phần bao gồm một tập hợp có quan hệ nhị phân phản xạ, phản đối xứng và bắc cầu. "Bộ có thứ tự từng phần" được viết tắt là POSET.

Ví dụ

Tập hợp các số thực trong phép toán nhị phân nhỏ hơn hoặc bằng $ (\ le) $ là một tập hợp.

Cho tập hợp $ S = \ lbrace 1, 2, 3 \ rbrace $ và phép toán là $ \ le $

Các quan hệ sẽ là $ \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) \ rbrace $

Mối quan hệ R này phản xạ dưới dạng $ \ lbrace (1, 1), (2, 2), (3, 3) \ rbrace \ in R $

Mối quan hệ R này là phản đối xứng, như

$ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace \ in R \ và \ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace ∉ R $

Mối quan hệ R này cũng có tính bắc cầu như $ \ lbrace (1,2), (2,3), (1,3) \ rbrace \ in R $.

Do đó, nó là một poset.
Tập đỉnh của một đồ thị xoay chiều có hướng trong phép toán 'khả năng truy cập' là một tập hợp.

Sơ đồ Hasse

Biểu đồ Hasse của poset là đồ thị có hướng mà các đỉnh là phần tử của poset đó và các cung bao trùm các cặp (x, y) trong poset. Nếu trong poset $ x <y $, thì điểm x xuất hiện thấp hơn điểm y trong biểu đồ Hasse. Nếu $ x <y <z $ trong poset, thì mũi tên không được hiển thị giữa x và z vì nó là ẩn.

Thí dụ

Vị trí của các tập con $ \ lbrace 1, 2, 3 \ rbrace = \ lbrace \ blankset, \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace, \ lbrace 1, 2 \ rbrace, \ lbrace 1 , 3 \ rbrace, \ lbrace 2, 3 \ rbrace, \ lbrace 1, 2, 3 \ rbrace \ rbrace $ được hiển thị bằng biểu đồ Hasse sau:

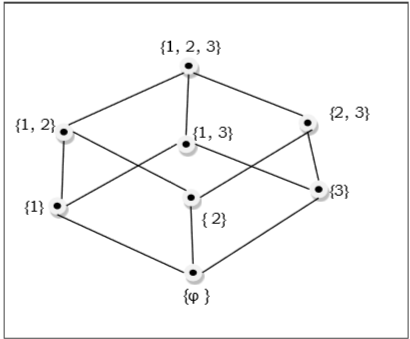
Bộ có thứ tự tuyến tính

Tập hợp có thứ tự tuyến tính hay Tập hợp có thứ tự toàn phần là một tập hợp thứ tự từng phần trong đó mọi cặp phần tử đều có thể so sánh được. Các phần tử $ a, b \ trong S $ được cho là có thể so sánh được nếu $ a \ le b $ hoặc $ b \ le a $ giữ nguyên. Luật tam giác xác định tổng bộ có thứ tự này. Một tập hợp có thứ tự hoàn toàn có thể được định nghĩa là một mạng phân phối có thuộc tính $ \ lbrace a \ lor b, a \ land b \ rbrace = \ lbrace a, b \ rbrace $ với tất cả các giá trị của a và b trong tập S.

Thí dụ

Tập lũy thừa của $ \ lbrace a, b \ rbrace $ được sắp xếp theo \ subseteq là một tập hợp có thứ tự hoàn toàn vì tất cả các phần tử của tập hợp lũy thừa $ P = \ lbrace \ blankset, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace a, b \ rbrace \ rbrace $ có thể so sánh được.

Ví dụ về bộ đơn hàng không tổng

Tập hợp $ S = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ trong phép toán x chia y không phải là một tập hợp có thứ tự.

Đây, cho tất cả $ (x, y) \ trong S, x | y $ phải giữ nhưng nó không đúng rằng 2 | 3, vì 2 không chia 3 hoặc 3 không chia 2. Do đó, nó không phải là một bộ tổng có thứ tự.

Mạng lưới

Mạng tinh thể là một tập hợp $ (L, \ le) $ mà mọi cặp $ \ lbrace a, b \ rbrace \ trong L $ có giới hạn trên nhỏ nhất (ký hiệu là $ a \ lor b $) và giới hạn dưới lớn nhất ( ký hiệu là $ a \ land b $). LUB $ (\ lbrace a, b \ rbrace) $ được gọi là phép nối của a và b. GLB $ (\ lbrace a, b \ rbrace) $ được gọi là giao điểm của a và b.

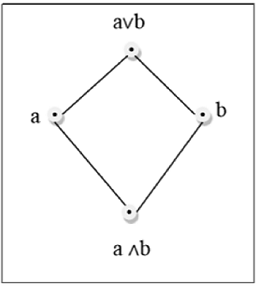
Thí dụ

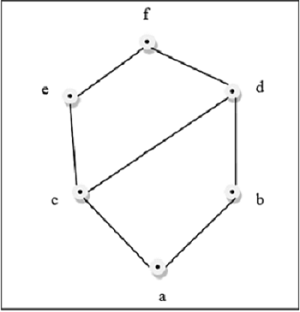
Hình trên là một mạng tinh thể vì với mỗi cặp $ \ lbrace a, b \ rbrace \ in L $, tồn tại một GLB và một LUB.

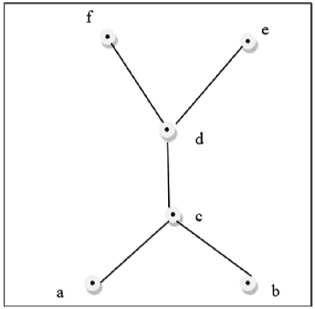
Hình trên không phải là một mạng tinh thể vì $ GLB (a, b) $ và $ LUB (e, f) $ không tồn tại.

Một số mạng khác được thảo luận dưới đây:

Mạng lưới

Một mạng tinh thể L trở thành mạng có giới hạn nếu nó có phần tử lớn nhất là 1 và phần tử nhỏ nhất là 0.

Mạng lưới bổ sung

Một mạng tinh thể L trở thành một mạng bổ sung nếu nó là một mạng liên kết và nếu mọi phần tử trong mạng có một phần bù. Phần tử x có phần bù x 'nếu $ \ tồn tại x (x \ land x' = 0 và x \ lor x '= 1) $