Toán học rời rạc - Nhiều hơn trên đồ thị

Tô màu đồ thị

Tô màu đồ thị là quy trình gán màu cho mỗi đỉnh của đồ thị G sao cho không có đỉnh liền kề nào có cùng màu. Mục tiêu là để giảm thiểu số lượng màu trong khi tô màu một biểu đồ. Số màu nhỏ nhất cần thiết để tô màu một đồ thị G được gọi là số màu của đồ thị đó. Bài toán tô màu đồ thị là một bài toán NP Complete.

Phương pháp tô màu đồ thị

Các bước cần thiết để tô màu một đồ thị G với n số đỉnh như sau:

Step 1 - Sắp xếp các đỉnh của đồ thị theo một thứ tự nào đó.

Step 2 - Chọn đỉnh đầu tiên và tô màu nó với màu đầu tiên.

Step 3- Chọn đỉnh tiếp theo và tô màu với màu đánh số thấp nhất chưa được tô màu trên bất kỳ đỉnh nào liền kề với nó. Nếu tất cả các đỉnh liền kề được tô bằng màu này, hãy gán một màu mới cho nó. Lặp lại bước này cho đến khi tất cả các đỉnh được tô màu.

Example

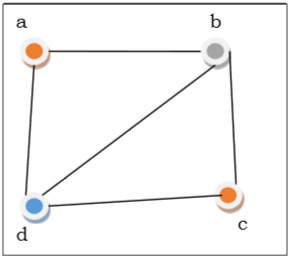
Trong hình trên, lúc đầu đỉnh $ a $ có màu đỏ. Khi các đỉnh liền kề của đỉnh a lại tiếp giáp với nhau, đỉnh $ b $ và đỉnh $ d $ được tô màu lần lượt là màu xanh lá cây và xanh lam. Khi đó đỉnh $ c $ được tô màu đỏ vì không có đỉnh nào liền kề của $ c $ được tô màu đỏ. Do đó, chúng tôi có thể tô màu biểu đồ bằng 3 màu. Do đó, số màu của đồ thị là 3.

Các ứng dụng của tô màu đồ thị

Một số ứng dụng của tô màu đồ thị bao gồm:

Đăng ký phân bổ
Tô màu bản đồ
Kiểm tra đồ thị lưỡng cực
Ấn định tần số vô tuyến điện thoại di động
Lập bảng thời gian, v.v.

Truyền tải đồ thị

Duyệt đồ thị là vấn đề thăm tất cả các đỉnh của đồ thị theo một số thứ tự có hệ thống. Chủ yếu có hai cách để đi qua một đồ thị.

Tìm kiếm đầu tiên theo chiều rộng
Tìm kiếm sâu đầu tiên

Tìm kiếm đầu tiên theo chiều rộng

Tìm kiếm đầu tiên theo chiều rộng (BFS) bắt đầu từ đỉnh cấp 0 bắt đầu $ X $ của biểu đồ $ G $. Sau đó, chúng tôi thăm tất cả các đỉnh là lân cận của $ X $. Sau khi tham quan, chúng tôi đánh dấu các đỉnh là "đã thăm" và đặt chúng vào cấp 1. Sau đó, chúng ta bắt đầu từ các đỉnh cấp 1 và áp dụng cùng một phương pháp trên mọi đỉnh cấp 1, v.v. Đường ngang BFS kết thúc khi mọi đỉnh của đồ thị đã được truy cập.

BFS Algorithm

Khái niệm là thăm tất cả các đỉnh lân cận trước khi thăm các đỉnh lân cận khác của các đỉnh lân cận.

Trạng thái khởi tạo của tất cả các nút là “Sẵn sàng”.
Đặt đỉnh nguồn vào hàng đợi và thay đổi trạng thái của nó thành “Đang chờ”.
Lặp lại hai bước sau cho đến khi hàng đợi trống -
- Xóa đỉnh đầu tiên khỏi hàng đợi và đánh dấu nó là “Đã truy cập”.
- Thêm vào phía sau hàng đợi tất cả các lân cận của đỉnh đã loại bỏ có trạng thái là “Sẵn sàng”. Đánh dấu trạng thái của họ là "Đang chờ".

Problem

Chúng ta hãy lấy một đồ thị (Đỉnh nguồn là 'a') và áp dụng thuật toán BFS để tìm ra thứ tự truyền tải.

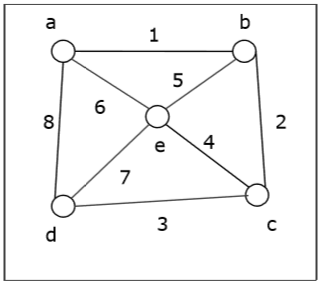
Solution -

Khởi tạo trạng thái của tất cả các đỉnh thành “Sẵn sàng”.
Đặt một trong hàng đợi và thay đổi trạng thái của mình để “chờ”.
Xóa một khỏi hàng đợi, đánh dấu nó là “Đã ghé thăm”.
Thêm một ‘s láng giềng trong‘Sẵn sàng’nhà nước b, d và e đến cuối hàng đợi và đánh dấu chúng là‘chờ đợi’.
Xóa b khỏi hàng đợi, đánh dấu là “Đã ghé thăm”, đặt hàng xóm c “Sẵn sàng” vào cuối hàng và đánh dấu c là “Đang chờ”.
Xóa d khỏi hàng đợi và đánh dấu là "Đã ghé thăm". Nó không có hàng xóm ở trạng thái "Sẵn sàng".
Xóa e khỏi hàng đợi và đánh dấu là "Đã ghé thăm". Nó không có hàng xóm ở trạng thái "Sẵn sàng".
Xóa c khỏi hàng đợi và đánh dấu là “Đã ghé thăm”. Nó không có hàng xóm ở trạng thái "Sẵn sàng".
Hàng đợi trống vì vậy hãy dừng lại.

Vì vậy, thứ tự duyệt là -

$ a \ rightarrow b \ rightarrow d \ rightarrow e \ rightarrow c $

Các thứ tự thay thế của truyền tải là -

$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $

Hoặc $ a \ rightarrow d \ rightarrow b \ rightarrow e \ rightarrow c $

Hoặc $ a \ rightarrow e \ rightarrow b \ rightarrow d \ rightarrow c $

Hoặc $ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $

Hoặc $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $

Application of BFS

Tìm con đường ngắn nhất
Cây bao trùm tối thiểu cho đồ thị không có trọng số
Hệ thống định vị GPS
Phát hiện các chu kỳ trong một đồ thị vô hướng
Tìm tất cả các nút trong một thành phần được kết nối

Complexity Analysis

Gọi $ G (V, E) $ là một đồ thị có $ | V | $ số đỉnh và $ | E | $ số cạnh. Nếu thuật toán tìm kiếm đầu tiên theo chiều rộng truy cập mọi đỉnh trong biểu đồ và kiểm tra mọi cạnh, thì độ phức tạp về thời gian của nó sẽ là:

$$ O (| V | + | E |). O (| E |) $$

Nó có thể khác nhau giữa $ O (1) $ và $ O (| V2 |) $

Tìm kiếm sâu đầu tiên

Thuật toán Tìm kiếm đầu tiên theo chiều sâu (DFS) bắt đầu từ đỉnh $ v $, sau đó nó đi qua đỉnh liền kề của nó (giả sử x) mà chưa được truy cập trước đó và đánh dấu là "đã thăm" và tiếp tục với đỉnh liền kề của $ x $ và Sớm.

Nếu tại bất kỳ đỉnh nào, nó gặp rằng tất cả các đỉnh liền kề được thăm, thì nó sẽ lùi lại cho đến khi nó tìm thấy đỉnh đầu tiên có một đỉnh liền kề mà trước đó chưa được duyệt qua. Sau đó, nó đi qua đỉnh đó, tiếp tục với các đỉnh liền kề của nó cho đến khi nó đi qua tất cả các đỉnh đã thăm và phải quay lại một lần nữa. Bằng cách này, nó sẽ đi qua tất cả các đỉnh có thể đạt được từ đỉnh ban đầu $ v $.

DFS Algorithm

Khái niệm này là thăm tất cả các đỉnh lân cận của một đỉnh lân cận trước khi thăm các đỉnh lân cận khác.

Khởi tạo trạng thái của tất cả các nút là “Sẵn sàng”
Đặt đỉnh nguồn vào một ngăn xếp và thay đổi trạng thái của nó thành "Đang chờ"
Lặp lại hai bước sau cho đến khi ngăn xếp trống -
- Bật đỉnh trên cùng từ ngăn xếp và đánh dấu nó là “Đã ghé thăm”
- Đẩy lên trên cùng của ngăn xếp tất cả các lân cận của đỉnh đã loại bỏ có trạng thái là “Sẵn sàng”. Đánh dấu trạng thái của họ là "Đang chờ".

Problem

Chúng ta hãy lấy một đồ thị (đỉnh nguồn là 'a') và áp dụng thuật toán DFS để tìm ra thứ tự truyền tải.

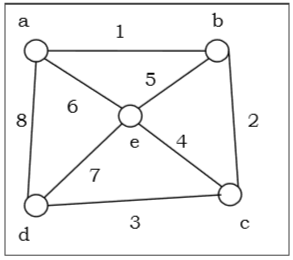
Solution

Khởi tạo trạng thái của tất cả các đỉnh thành “Sẵn sàng”.
Đẩy một ngăn xếp vào và thay đổi trạng thái của nó thành “Đang chờ”.
Bật a và đánh dấu là “Đã ghé thăm”.
Đẩy một người hàng xóm ‘s trong‘Sẵn sàng’tình trạng e, d và b để đầu ngăn xếp và đánh dấu chúng là‘chờ đợi’.
Bật b từ ngăn xếp, đánh dấu là "Đã thăm", đẩy hàng xóm "Sẵn sàng" c lên ngăn xếp.
Bật c từ ngăn xếp và đánh dấu là "Đã truy cập". Nó không có hàng xóm "Sẵn sàng".
Bật d từ ngăn xếp và đánh dấu là "Đã truy cập". Nó không có hàng xóm "Sẵn sàng".
Bật e từ ngăn xếp và đánh dấu là "Đã truy cập". Nó không có hàng xóm "Sẵn sàng".
Ngăn xếp trống. Vì vậy, hãy dừng lại.

Vì vậy, thứ tự duyệt là -

$ a \ rightarrow b \ rightarrow c \ rightarrow d \ rightarrow e $

Các thứ tự thay thế của truyền tải là -

$ a \ rightarrow e \ rightarrow b \ rightarrow c \ rightarrow d $

Hoặc $ a \ rightarrow b \ rightarrow e \ rightarrow c \ rightarrow d $

Hoặc $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $

Hoặc $ a \ rightarrow d \ rightarrow c \ rightarrow e \ rightarrow b $

Hoặc $ a \ rightarrow d \ rightarrow c \ rightarrow b \ rightarrow e $

Complexity Analysis

Gọi $ G (V, E) $ là một đồ thị có $ | V | $ số đỉnh và $ | E | $ số cạnh. Nếu thuật toán DFS truy cập mọi đỉnh trong đồ thị và kiểm tra mọi cạnh, thì độ phức tạp về thời gian là:

$$ \ circleleddash (| V | + | E |) $$

Applications

Phát hiện chu kỳ trong biểu đồ
Để tìm cách sắp xếp theo cấu trúc liên kết
Để kiểm tra xem một biểu đồ có phải là lưỡng phân không
Tìm các thành phần được kết nối
Tìm cầu của một đồ thị
Tìm kết nối sinh học trong biểu đồ
Giải quyết vấn đề về Chuyến du lịch của Hiệp sĩ
Giải các câu đố chỉ với một giải pháp