Toán học rời rạc - Hướng dẫn nhanh

Toán học có thể được phân thành hai loại:

• Continuous Mathematics- Nó dựa trên dòng số liên tục hoặc các số thực. Nó được đặc trưng bởi thực tế là giữa hai số bất kỳ, hầu như luôn luôn có một tập hợp số vô hạn. Ví dụ, một hàm trong toán học liên tục có thể được vẽ theo một đường cong trơn mà không có dấu ngắt.

• Discrete Mathematics- Nó liên quan đến các giá trị khác biệt; tức là giữa hai điểm bất kỳ có một số điểm đếm được. Ví dụ, nếu chúng ta có một tập hợp hữu hạn các đối tượng, hàm có thể được định nghĩa là một danh sách các cặp có thứ tự có các đối tượng này và có thể được trình bày dưới dạng danh sách đầy đủ các cặp đó.

Các chủ đề về Toán học rời rạc

Mặc dù không thể có một số nhánh nhất định của Toán học rời rạc, các chủ đề sau đây hầu như luôn được đề cập trong bất kỳ nghiên cứu nào liên quan đến vấn đề này -

• Bộ, Quan hệ và Hàm
• Logic toán học
• Lý thuyết nhóm
• Lý thuyết đếm
• Probability
• Quy nạp toán học và quan hệ lặp lại
• Lý thuyết đồ thị
• Trees
• Đại số Boolean

Chúng ta sẽ thảo luận về từng khái niệm này trong các chương tiếp theo của hướng dẫn này.

Nhà toán học người Đức G. Cantorgiới thiệu khái niệm tập hợp. Ông đã định nghĩa một tập hợp là một tập hợp các đối tượng xác định và có thể phân biệt được lựa chọn bằng các quy tắc hoặc mô tả nhất định.

Setlý thuyết là cơ sở của một số lĩnh vực nghiên cứu khác như lý thuyết đếm, quan hệ, lý thuyết đồ thị và máy trạng thái hữu hạn. Trong chương này, chúng tôi sẽ đề cập đến các khía cạnh khác nhau củaSet Theory.

Đặt - Định nghĩa

Tập hợp là một tập hợp không có thứ tự của các phần tử khác nhau. Một tập hợp có thể được viết rõ ràng bằng cách liệt kê các phần tử của nó bằng dấu ngoặc vuông. Nếu thứ tự của các phần tử bị thay đổi hoặc bất kỳ phần tử nào của một tập hợp được lặp lại, nó sẽ không tạo ra bất kỳ thay đổi nào trong tập hợp.

Một số ví dụ về bộ

• Tập hợp tất cả các số nguyên dương
• Tập hợp tất cả các hành tinh trong hệ mặt trời
• Một tập hợp tất cả các tiểu bang ở Ấn Độ
• Một tập hợp tất cả các chữ cái thường của bảng chữ cái

Đại diện của một Tập hợp

Tập hợp có thể được biểu diễn theo hai cách:

• Bảng phân công hoặc Biểu mẫu
• Đặt ký hiệu trình tạo

Bảng phân công hoặc Biểu mẫu

Tập hợp được biểu diễn bằng cách liệt kê tất cả các phần tử bao gồm nó. Các phần tử được đặt trong dấu ngoặc nhọn và được phân tách bằng dấu phẩy.

Example 1 - Tập hợp các nguyên âm trong bảng chữ cái tiếng Anh, $A = \lbrace a,e,i,o,u \rbrace$

Example 2 - Tập hợp các số lẻ nhỏ hơn 10, $B = \lbrace 1,3,5,7,9 \rbrace$

Đặt ký hiệu trình tạo

Tập hợp được xác định bằng cách chỉ định một thuộc tính mà các phần tử của tập hợp có điểm chung. Bộ được mô tả là$A = \lbrace x : p(x) \rbrace$

Example 1 - Bộ $\lbrace a,e,i,o,u \rbrace$ được viết là -

$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$

Example 2 - Bộ $\lbrace 1,3,5,7,9 \rbrace$ được viết là -

$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$

Nếu một phần tử x là thành viên của tập S bất kỳ, nó được ký hiệu là $x \in S$ và nếu một phần tử y không phải là thành viên của tập S, nó được ký hiệu là $y \notin S$.

Example- Nếu$S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ nhưng $1.5 \notin S$

Một số bộ quan trọng

N - tập hợp tất cả các số tự nhiên = $\lbrace1, 2, 3, 4, .....\rbrace$

Z - tập hợp tất cả các số nguyên = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$

Z⁺ - tập hợp tất cả các số nguyên dương

Q - tập hợp tất cả các số hữu tỉ

R - tập hợp tất cả các số thực

W - tập hợp tất cả các số nguyên

Số lượng của một tập hợp

Số lượng của một tập hợp S, ký hiệu là $|S|$, là số phần tử của tập hợp. Con số này cũng được gọi là số chính. Nếu một tập hợp có vô số phần tử, thì tổng số của nó là$\infty$.

Example - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$

Nếu có hai tập X và Y,

• $|X| = |Y|$biểu thị hai tập X và Y có cùng một bản số. Nó xảy ra khi số phần tử trong X đúng bằng số phần tử trong Y. Trong trường hợp này, tồn tại một hàm phân tích 'f' từ X đến Y.

• $|X| \le |Y|$biểu thị rằng bản số của tập hợp X nhỏ hơn hoặc bằng bản số của tập hợp Y. Nó xảy ra khi số phần tử trong X nhỏ hơn hoặc bằng Y. Ở đây, tồn tại một hàm bất biến 'f' từ X đến Y.

• $|X| \lt |Y|$biểu thị rằng cardinality của tập X nhỏ hơn cardinality của tập Y. Nó xảy ra khi số phần tử trong X ít hơn Y. Ở đây, hàm 'f' từ X đến Y là hàm không xác định nhưng không phải là hàm phân vị.

• $If\ |X| \le |Y|$ và $|X| \ge |Y|$ sau đó $|X| = |Y|$. Các tập X và Y thường được gọi là các tập tương đương.

Các loại bộ

Bộ có thể được phân thành nhiều loại. Một số trong số đó là hữu hạn, vô hạn, tập con, phổ quát, thích hợp, tập đơn, v.v.

Tập hợp hữu hạn

Một tập hợp chứa một số phần tử xác định được gọi là tập hợp hữu hạn.

Example - $S = \lbrace x \:| \:x \in N$ và $70 \gt x \gt 50 \rbrace$

Bộ vô hạn

Tập hợp chứa vô số phần tử được gọi là tập hợp vô hạn.

Example - $S = \lbrace x \: | \: x \in N $ và $ x \gt 10 \rbrace$

Tập hợp con

Tập hợp X là tập hợp con của tập hợp Y (Được viết là $X \subseteq Y$) nếu mọi phần tử của X là phần tử của tập Y.

Example 1 - Để, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ và $Y = \lbrace 1, 2 \rbrace$. Ở đây tập Y là một tập con của tập X vì tất cả các phần tử của tập Y đều nằm trong tập X. Do đó, chúng ta có thể viết$Y \subseteq X$.

Example 2 - Để, $X = \lbrace 1, 2, 3 \rbrace$ và $Y = \lbrace 1, 2, 3 \rbrace$. Ở đây tập Y là một tập hợp con (Không phải là một tập hợp con thích hợp) của tập X vì tất cả các phần tử của tập Y đều nằm trong tập X. Do đó, chúng ta có thể viết$Y \subseteq X$.

Tập số thực

Thuật ngữ "tập hợp con thích hợp" có thể được định nghĩa là "tập hợp con của nhưng không bằng". Tập hợp X là một tập hợp con thích hợp của tập hợp Y (Được viết là$ X \subset Y $) nếu mọi phần tử của X là phần tử của tập Y và $|X| \lt |Y|$.

Example - Để, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ và $Y = \lbrace 1, 2 \rbrace$. Đây là bộ$Y \subset X$ vì tất cả các yếu tố trong $Y$ được chứa trong $X$ quá và $X$ có ít nhất một phần tử nhiều hơn bộ $Y$.

Bộ phổ quát

Nó là một tập hợp của tất cả các yếu tố trong một ngữ cảnh hoặc ứng dụng cụ thể. Tất cả các tập hợp trong ngữ cảnh hoặc ứng dụng đó về cơ bản là tập hợp con của tập hợp phổ quát này. Tập hợp phổ quát được biểu diễn dưới dạng$U$.

Example - Chúng tôi có thể xác định $U$như tập hợp của tất cả các loài động vật trên trái đất. Trong trường hợp này, tập hợp tất cả các loài động vật có vú là tập hợp con của$U$, tập hợp tất cả các loài cá là tập hợp con của $U$, tập hợp tất cả các loài côn trùng là một tập hợp con của $U$, và như thế.

Tập hợp rỗng hoặc tập hợp rỗng

Một tập hợp rỗng không chứa phần tử nào. Nó được ký hiệu là$\emptyset$. Vì số phần tử trong một tập hợp rỗng là hữu hạn, nên tập hợp rỗng là một tập hợp hữu hạn. Cardinality của tập hợp rỗng hoặc tập hợp rỗng bằng không.

Example - $S = \lbrace x \:| \: x \in N$ và $7 \lt x \lt 8 \rbrace = \emptyset$

Bộ Singleton hoặc Bộ đơn vị

Tập hợp đơn hoặc tập đơn vị chỉ chứa một phần tử. Một tập hợp singleton được ký hiệu là$\lbrace s \rbrace$.

Example - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$

Bộ bằng

Nếu hai tập hợp chứa các phần tử giống nhau thì chúng được cho là bằng nhau.

Example - Nếu $A = \lbrace 1, 2, 6 \rbrace$ và $B = \lbrace 6, 1, 2 \rbrace$, chúng bằng nhau vì mọi phần tử của tập A đều là phần tử của tập B và mọi phần tử của tập B đều là phần tử của tập A.

Bộ tương đương

Nếu các thẻ số của hai tập hợp giống nhau, chúng được gọi là tập hợp tương đương.

Example - Nếu $A = \lbrace 1, 2, 6 \rbrace$ và $B = \lbrace 16, 17, 22 \rbrace$, chúng tương đương vì bản số của A bằng bản số của B. tức là $|A| = |B| = 3$

Bộ chồng chéo

Hai tập hợp có ít nhất một phần tử chung được gọi là tập hợp trùng nhau.

Trong trường hợp các tập hợp chồng chéo -

• $n(A \cup B) = n(A) + n(B) - n(A \cap B)$

• $n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$

• $n(A) = n(A - B) + n(A \cap B)$

• $n(B) = n(B - A) + n(A \cap B)$

Example - Để, $A = \lbrace 1, 2, 6 \rbrace$ và $B = \lbrace 6, 12, 42 \rbrace$. Có một phần tử chung '6', do đó các tập hợp này là các tập hợp chồng chéo.

Bộ rời

Hai tập hợp A và B được gọi là tập rời nếu chúng không có chung một phần tử. Do đó, các bộ rời rạc có các thuộc tính sau:

• $n(A \cap B) = \emptyset$

• $n(A \cup B) = n(A) + n(B)$

Example - Để, $A = \lbrace 1, 2, 6 \rbrace$ và $B = \lbrace 7, 9, 14 \rbrace$, không có một phần tử chung duy nhất, do đó các tập hợp này là các tập hợp chồng chéo.

Sơ đồ Venn

Biểu đồ Venn, được phát minh vào năm 1880 bởi John Venn, là một biểu đồ thể hiện tất cả các quan hệ logic có thể có giữa các tập hợp toán học khác nhau.

Examples

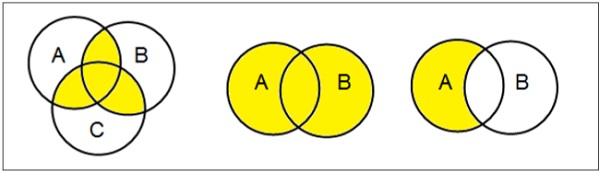
Đặt hoạt động

Các phép toán tập hợp bao gồm tập hợp Liên hiệp, Giao điểm tập hợp, Sự khác biệt của tập hợp, Sự bổ sung của tập hợp và Tích Descartes.

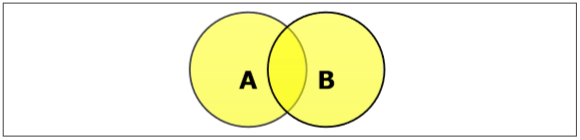
Đặt Union

Sự kết hợp của tập hợp A và B (ký hiệu là $A \cup B$) là tập hợp các phần tử nằm trong A, trong B, hoặc cả A và B. Do đó, $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$.

Example - Nếu $A = \lbrace 10, 11, 12, 13 \rbrace$ và B = $\lbrace 13, 14, 15 \rbrace$, sau đó $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$. (Phần tử chung chỉ xảy ra một lần)

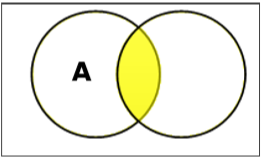
Đặt giao lộ

Giao của tập A và B (ký hiệu là $A \cap B$) là tập hợp các phần tử ở cả A và B. Do đó, $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$.

Example - Nếu $A = \lbrace 11, 12, 13 \rbrace$ và $B = \lbrace 13, 14, 15 \rbrace$, sau đó $A \cap B = \lbrace 13 \rbrace$.

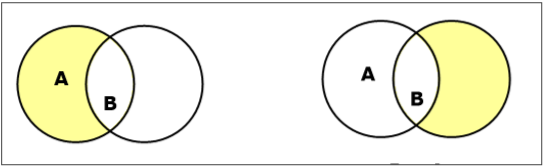
Đặt sự khác biệt / Bổ sung tương đối

Hiệu số tập hợp của tập hợp A và tập hợp B (ký hiệu là $A – B$) là tập hợp các phần tử chỉ nằm trong A mà không nằm trong B. Do đó, $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$.

Example - Nếu $A = \lbrace 10, 11, 12, 13 \rbrace$ và $B = \lbrace 13, 14, 15 \rbrace$, sau đó $(A - B) = \lbrace 10, 11, 12 \rbrace$ và $(B - A) = \lbrace 14, 15 \rbrace$. Ở đây, chúng ta có thể thấy$(A - B) \ne (B - A)$

Sự bổ sung của một bộ

Phần bù của tập A (ký hiệu là $A’$) là tập hợp các phần tử không có trong tập A. Do đó, $A' = \lbrace x | x \notin A \rbrace$.

Cụ thể hơn, $A'= (U - A)$ Ở đâu $U$ là một tập hợp phổ quát chứa tất cả các đối tượng.

Example - Nếu $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ sau đó $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$

Sản phẩm Descartes / Sản phẩm chéo

Tích số Descartes của n số bộ $A_1, A_2, \dots A_n$ biểu thị là $A_1 \times A_2 \dots \times A_n$ có thể được định nghĩa là tất cả các cặp có thứ tự có thể $(x_1, x_2, \dots x_n)$ Ở đâu $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$

Example - Nếu chúng ta lấy hai bộ $A = \lbrace a, b \rbrace$ và $B = \lbrace 1, 2 \rbrace$,

Tích Descartes của A và B được viết là - $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$

Tích Descartes của B và A được viết là - $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$

Bộ nguồn

Tập hợp lũy thừa của một tập S là tập hợp tất cả các tập con của S kể cả tập rỗng. Bản số của một tập hợp lũy thừa của một bộ S của bản số n là$2^n$. Bộ nguồn được ký hiệu là$P(S)$.

Example −

Đối với một bộ $S = \lbrace a, b, c, d \rbrace$ hãy để chúng tôi tính toán các tập hợp con -

• Tập hợp con có 0 phần tử - $\lbrace \emptyset \rbrace$ (bộ trống)

• Tập hợp con có 1 phần tử - $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$

• Tập con có 2 phần tử - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$

• Tập hợp con có 3 phần tử - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$

• Tập con có 4 phần tử - $\lbrace a, b, c, d \rbrace$

Vì thế, $P(S)=$

$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$

$| P(S) | = 2^4 = 16$

Note - Công suất của một tập hợp rỗng cũng là một tập hợp rỗng.

$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$

Phân vùng của một tập hợp

Phân vùng của một tập hợp, chẳng hạn như S , là tập hợp của n tập hợp con rời rạc, chẳng hạn$P_1, P_2, \dots P_n$ thỏa mãn ba điều kiện sau:

• $P_i$ không chứa tập hợp trống.

  $\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$

• Sự kết hợp của các tập hợp con phải bằng toàn bộ tập hợp ban đầu.

  $\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$

• Giao của bất kỳ hai tập hợp phân biệt nào là trống.

  $\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$

Example

Để cho $S = \lbrace a, b, c, d, e, f, g, h \rbrace$

Một phân vùng có thể xảy ra là $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$

Một phân vùng có thể xảy ra khác là $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$

Số chuông

Số chuông cho biết số cách phân vùng một tập hợp. Chúng được ký hiệu bởi$B_n$ với n là tổng số của tập hợp.

Example -

Để cho $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$

Các phân vùng thay thế là -

1. $\emptyset , \lbrace 1, 2, 3 \rbrace$

2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$

3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$

4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$

5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$

Vì thế $B_3 = 5$

Bất cứ khi nào các tập hợp đang được thảo luận, mối quan hệ giữa các phần tử của tập hợp là điều tiếp theo xuất hiện. Relations có thể tồn tại giữa các đối tượng của cùng một tập hợp hoặc giữa các đối tượng của hai hoặc nhiều tập hợp.

Định nghĩa và Thuộc tính

Một quan hệ nhị phân R từ tập hợp x đến y (được viết là $xRy$ hoặc là $R(x,y)$) là một tập con của tích Descartes $x \times y$. Nếu cặp thứ tự của G bị đảo ngược, quan hệ cũng thay đổi.

Nói chung là một quan hệ n-ary R giữa các tập hợp $A_1, \dots ,\ and\ A_n$ là một tập hợp con của sản phẩm n-ary $A_1 \times \dots \times A_n$. Số lượng tối thiểu của một quan hệ R là 0 và tối đa là$n^2$ trong trường hợp này.

Một quan hệ nhị phân R trên một tập đơn A là một tập con của $A \times A$.

Đối với hai tập phân biệt, A và B, có các hồng số tương ứng là m và n , thì tổng số lớn nhất của một quan hệ R từ A đến B là mn .

Tên miền và phạm vi

Nếu có hai tập hợp A và B và quan hệ R có cặp thứ tự (x, y), thì -

• Các domain của R, Dom (R), là tập hợp $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$

• Các range của R, Ran (R), là tập hợp $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$

Ví dụ

Để cho, $A = \lbrace 1, 2, 9 \rbrace $ và $ B = \lbrace 1, 3, 7 \rbrace$

• Trường hợp 1 - Nếu quan hệ R là 'bằng' thì $R = \lbrace (1, 1), (3, 3) \rbrace$

  Dom (R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$

• Trường hợp 2 - Nếu quan hệ R là 'nhỏ hơn' thì $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$

  Dom (R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$

• Trường hợp 3 - Nếu quan hệ R là 'lớn hơn' thì $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$

  Dom (R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$

Biểu diễn các mối quan hệ bằng cách sử dụng Đồ thị

Một quan hệ có thể được biểu diễn bằng biểu đồ có hướng.

Số đỉnh trong đồ thị bằng số phần tử trong tập hợp mà từ đó quan hệ đã được xác định. Với mỗi cặp có thứ tự (x, y) trong quan hệ R, sẽ có một cạnh có hướng từ đỉnh 'x' đến đỉnh 'y'. Nếu có một cặp có thứ tự (x, x), sẽ có vòng lặp tự trên đỉnh 'x'.

Giả sử, có một mối quan hệ $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ trên phim trường $S = \lbrace 1, 2, 3 \rbrace$, nó có thể được biểu diễn bằng biểu đồ sau:

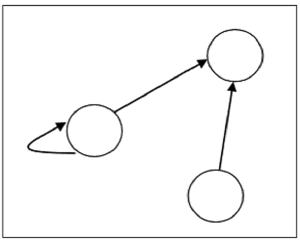
Các loại quan hệ

• Các Empty Relation giữa tập X và Y, hoặc trên E, là tập trống $\emptyset$

• Các Full Relation giữa tập X và Y là tập $X \times Y$

• Các Identity Relation trên tập X là tập $\lbrace (x, x) | x \in X \rbrace$

• Quan hệ nghịch đảo R 'của quan hệ R được định nghĩa là: $R' = \lbrace (b, a) | (a, b) \in R \rbrace$

  Example - Nếu $R = \lbrace (1, 2), (2, 3) \rbrace$ sau đó $R' $ sẽ là $\lbrace (2, 1), (3, 2) \rbrace$

• Một quan hệ R trên tập A được gọi là Reflexive nếu $\forall a \in A$ có liên quan đến a (aRa giữ)

  Example - Mối quan hệ $R = \lbrace (a, a), (b, b) \rbrace$ trên phim trường $X = \lbrace a, b \rbrace$ là phản xạ.

• Một quan hệ R trên tập A được gọi là Irreflexive nếu không $a \in A$ có liên quan đến a (aRa không giữ).

  Example - Mối quan hệ $R = \lbrace (a, b), (b, a) \rbrace$ trên phim trường $X = \lbrace a, b \rbrace$ là không linh hoạt.

• Một quan hệ R trên tập A được gọi là Symmetric nếu $xRy$ ngụ ý $yRx$, $\forall x \in A$ và $\forall y \in A$.

  Example - Mối quan hệ $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ trên phim trường $A = \lbrace 1, 2, 3 \rbrace$ là đối xứng.

• Một quan hệ R trên tập A được gọi là Anti-Symmetric nếu $xRy$ và $yRx$ ngụ ý $x = y \: \forall x \in A$ và $\forall y \in A$.

  Example - Mối quan hệ $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ là phản đối xứng kể từ $x \leq y$ và $y \leq x$ ngụ ý $x = y$.

• Một quan hệ R trên tập A được gọi là Transitive nếu $xRy$ và $yRz$ ngụ ý $xRz, \forall x,y,z \in A$.

  Example - Mối quan hệ $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ trên phim trường $A = \lbrace 1, 2, 3 \rbrace$ có tính bắc cầu.

• Một mối quan hệ là một Equivalence Relation nếu nó là phản xạ, đối xứng và bắc cầu.

  Example - Mối quan hệ $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ trên phim trường $A = \lbrace 1, 2, 3 \rbrace$ là một quan hệ tương đương vì nó là phản xạ, đối xứng và bắc cầu.

A Functiongán cho mỗi phần tử của một tập hợp, chính xác một phần tử của một tập hợp có liên quan. Các hàm tìm thấy ứng dụng của chúng trong các lĩnh vực khác nhau như biểu diễn độ phức tạp tính toán của các thuật toán, đếm đối tượng, nghiên cứu trình tự và chuỗi, cho đến tên một số. Chương thứ ba và cuối cùng của phần này nêu bật các khía cạnh quan trọng của chức năng.

Chức năng - Định nghĩa

Một hàm hoặc ánh xạ (Được định nghĩa là $f: X \rightarrow Y$) là mối quan hệ từ các phần tử của một tập X với các phần tử của một tập Y khác (X và Y là các tập khác rỗng). X được gọi là Miền và Y được gọi là Codomain của hàm 'f'.

Hàm 'f' là một quan hệ trên X và Y sao cho mỗi $x \in X$, tồn tại một $y \in Y$ như vậy mà $(x,y) \in R$. 'x' được gọi là tiền ảnh và 'y' được gọi là ảnh của hàm f.

Một hàm có thể là một với một hoặc nhiều với một nhưng không phải là một với nhiều.

Chức năng Injective / One-to-one

Một chức năng $f: A \rightarrow B$ là chức năng bị lỗi hoặc một đối một nếu cho mọi $b \in B$, tồn tại nhiều nhất một $a \in A$ như vậy mà $f(s) = t$.

Điều này có nghĩa là một chức năng f bị thương nếu $a_1 \ne a_2$ ngụ ý $f(a1) \ne f(a2)$.

Thí dụ

• $f: N \rightarrow N, f(x) = 5x$ bị thương.

• $f: N \rightarrow N, f(x) = x^2$ bị thương.

• $f: R\rightarrow R, f(x) = x^2$ không bị thương như $(-x)^2 = x^2$

Chức năng Surjective / Onto

Một chức năng $f: A \rightarrow B$là ảnh xạ ảnh (lên) nếu ảnh của f bằng khoảng của nó. Tương đương, cho mọi$b \in B$, có một số $a \in A$ như vậy mà $f(a) = b$. Điều này có nghĩa là với bất kỳ y nào trong B, tồn tại một số x trong A sao cho$y = f(x)$.

Thí dụ

• $f : N \rightarrow N, f(x) = x + 2$ là mặt khách quan.

• $f : R \rightarrow R, f(x) = x^2$ không phải là số phụ vì chúng ta không thể tìm thấy một số thực có bình phương là số âm.

Bijective / One-to-one Correspondent

Một chức năng $f: A \rightarrow B$ là thông tin viên khách quan hoặc một đối một nếu và chỉ khi f vừa là suy diễn vừa là chủ quan.

Vấn đề

Chứng minh rằng một hàm $f: R \rightarrow R$ Được định nghĩa bởi $f(x) = 2x – 3$ là một chức năng khách quan.

Explanation - Chúng ta phải chứng minh hàm này vừa có tính chất suy diễn vừa là hàm số phụ.

Nếu $f(x_1) = f(x_2)$, sau đó $2x_1 – 3 = 2x_2 – 3 $ và nó ngụ ý rằng $x_1 = x_2$.

Do đó, f là injective.

Đây, $2x – 3= y$

Vì thế, $x = (y+5)/3$ thuộc về R và $f(x) = y$.

Do đó, f là surjective.

Từ f là cả hai surjective và injective, chúng ta có thể nói f Là bijective.

Nghịch đảo của một hàm

Các inverse của một chức năng tương ứng một đối một $f : A \rightarrow B$, là chức năng $g : B \rightarrow A$, nắm giữ tài sản sau -

$f(x) = y \Leftrightarrow g(y) = x$

Hàm f được gọi là invertible, nếu hàm ngược g của nó tồn tại.

Thí dụ

• Một chức năng $f : Z \rightarrow Z, f(x)=x+5$, là khả nghịch vì nó có hàm ngược $ g : Z \rightarrow Z, g(x)= x-5$.

• Một chức năng $f : Z \rightarrow Z, f(x)=x^2$ không thể đảo ngược vì đây không phải là một đối một như $(-x)^2=x^2$.

Thành phần của các hàm

Hai chức năng $f: A \rightarrow B$ và $g: B \rightarrow C$ có thể được sáng tác để đưa ra một bố cục $g o f$. Đây là một hàm từ A đến C được xác định bởi$(gof)(x) = g(f(x))$

Thí dụ

Để cho $f(x) = x + 2$ và $g(x) = 2x + 1$, tìm thấy $( f o g)(x)$ và $( g o f)(x)$.

Giải pháp

$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$

$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$

Vì thế, $(f o g)(x) \neq (g o f)(x)$

Một số thông tin về thành phần

• Nếu f và g là một đối một thì hàm $(g o f)$ cũng là một đối một.

• Nếu f và g nằm trên thì hàm $(g o f)$ cũng đang vào.

• Thành phần luôn giữ tài sản liên kết nhưng không giữ tài sản giao hoán.

Các quy tắc logic toán học chỉ rõ các phương pháp lập luận các câu lệnh toán học. Nhà triết học Hy Lạp, Aristotle, là người tiên phong của suy luận lôgic. Suy luận logic cung cấp cơ sở lý thuyết cho nhiều lĩnh vực toán học và do đó là khoa học máy tính. Nó có nhiều ứng dụng thực tế trong khoa học máy tính như thiết kế máy tính, trí tuệ nhân tạo, định nghĩa cấu trúc dữ liệu cho ngôn ngữ lập trình, v.v.

Propositional Logicliên quan đến các tuyên bố mà giá trị sự thật, "đúng" và "sai", có thể được chỉ định. Mục đích là để phân tích các tuyên bố này hoặc riêng lẻ hoặc theo cách tổng hợp.

Logic giới từ - Định nghĩa

Mệnh đề là tập hợp các câu lệnh khai báo có giá trị chân lý "true" hoặc giá trị chân lý "false". Mệnh đề bao gồm các biến mệnh đề và các phép liên kết. Chúng tôi biểu thị các biến mệnh đề bằng chữ in hoa (A, B, v.v.). Các phép nối kết nối các biến mệnh đề.

Một số ví dụ về Mệnh đề được đưa ra dưới đây:

• "Man is Mortal", nó trả về giá trị sự thật "TRUE"
• "12 + 9 = 3 - 2", nó trả về giá trị sự thật "FALSE"

Sau đây không phải là một Đề xuất -

• "A nhỏ hơn 2". Đó là bởi vì trừ khi chúng ta đưa ra một giá trị cụ thể của A, chúng ta không thể nói liệu tuyên bố đó là đúng hay sai.

Kết nối

Trong logic mệnh đề nói chung, chúng ta sử dụng năm kết nối là:

• HOẶC LÀ ($\lor$)

• VÀ ($\land$)

• Phủ định / KHÔNG ($\lnot$)

• Hàm ý / nếu-thì ($\rightarrow$)

• Nếu và chỉ nếu ($\Leftrightarrow$).

OR ($\lor$) - Phép toán OR của hai mệnh đề A và B (viết là $A \lor B$) là đúng nếu ít nhất bất kỳ biến mệnh đề A hoặc B là đúng.

Bảng sự thật như sau:

A	B	A ∨ B
Thật	Thật	Thật
Thật	Sai	Thật
Sai	Thật	Thật
Sai	Sai	Sai

AND ($\land$) - Phép toán AND của hai mệnh đề A và B (viết là $A \land B$) là đúng nếu cả biến mệnh đề A và B đều đúng.

Bảng sự thật như sau:

A	B	A ∧ B
Thật	Thật	Thật
Thật	Sai	Sai
Sai	Thật	Sai
Sai	Sai	Sai

Negation ($\lnot$) - Sự phủ định của mệnh đề A (được viết là $\lnot A$) sai khi A đúng và đúng khi A sai.

Bảng sự thật như sau:

A	¬ A
Thật	Sai
Sai	Thật

Implication / if-then ($\rightarrow$) - Một hàm ý $A \rightarrow B$là mệnh đề “nếu A, thì B”. Nếu A đúng và B sai. Các trường hợp còn lại là đúng.

Bảng sự thật như sau:

A	B	A → B
Thật	Thật	Thật
Thật	Sai	Sai
Sai	Thật	Thật
Sai	Sai	Thật

If and only if ($ \Leftrightarrow $) - $A \Leftrightarrow B$ là liên kết logic hai điều kiện đúng khi p và q giống nhau, tức là cả hai đều sai hoặc cả hai đều đúng.

Bảng sự thật như sau:

A	B	A ⇔ B
Thật	Thật	Thật
Thật	Sai	Sai
Sai	Thật	Sai
Sai	Sai	Thật

Tautologies

Tautology là một công thức luôn đúng với mọi giá trị của các biến mệnh đề của nó.

Example - Chứng minh $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ là một sự căng thẳng

Bảng sự thật như sau:

A	B	A → B	(A → B) ∧ A	[(A → B) ∧ A] → B
Thật	Thật	Thật	Thật	Thật
Thật	Sai	Sai	Sai	Thật
Sai	Thật	Thật	Sai	Thật
Sai	Sai	Thật	Sai	Thật

Như chúng ta có thể thấy mọi giá trị của $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ là "Đúng", nó là một sự phản phục.

Mâu thuẫn

Mâu thuẫn là một công thức luôn sai đối với mọi giá trị của các biến mệnh đề của nó.

Example - Chứng minh $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ là một sự mâu thuẫn

Bảng sự thật như sau:

A	B	A ∨ B	¬ A	¬ B	(¬ A) ∧ (¬ B)	(A ∨ B) ∧ [(¬ A) ∧ (¬ B)]
Thật	Thật	Thật	Sai	Sai	Sai	Sai
Thật	Sai	Thật	Sai	Thật	Sai	Sai
Sai	Thật	Thật	Thật	Sai	Sai	Sai
Sai	Sai	Sai	Thật	Thật	Thật	Sai

Như chúng ta có thể thấy mọi giá trị của $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ là "Sai", nó là một mâu thuẫn.

Dự phòng

Dự phòng là một công thức có cả một số giá trị đúng và một số giá trị sai cho mọi giá trị của các biến mệnh đề của nó.

Example - Chứng minh $(A \lor B) \land (\lnot A)$ một sự dự phòng

Bảng sự thật như sau:

A	B	A ∨ B	¬ A	(A ∨ B) ∧ (¬ A)
Thật	Thật	Thật	Sai	Sai
Thật	Sai	Thật	Sai	Sai
Sai	Thật	Thật	Thật	Thật
Sai	Sai	Sai	Thật	Sai

Như chúng ta có thể thấy mọi giá trị của $(A \lor B) \land (\lnot A)$ có cả "Đúng" và "Sai", nó là một trường hợp dự phòng.

Tương đương mệnh đề

Hai câu lệnh X và Y tương đương về mặt logic nếu bất kỳ điều kiện nào trong hai điều kiện sau đây:

• Các bảng chân trị của mỗi câu lệnh có cùng giá trị chân lý.

• Câu lệnh điều kiện hai $X \Leftrightarrow Y$ là một sự phản phục.

Example - Chứng minh $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ tương đương nhau

Kiểm tra bởi 1 ^st phương pháp (bảng sự thật Matching)

A	B	A ∨ B	¬ (A ∨ B)	¬ A	¬ B	[(¬ A) ∧ (¬ B)]
Thật	Thật	Thật	Sai	Sai	Sai	Sai
Thật	Sai	Thật	Sai	Sai	Thật	Sai
Sai	Thật	Thật	Sai	Thật	Sai	Sai
Sai	Sai	Sai	Thật	Thật	Thật	Thật

Ở đây, chúng ta có thể thấy giá trị sự thật của $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ giống nhau, do đó các câu lệnh là tương đương.

Kiểm tra bằng phương pháp ^{thứ 2} (Điều kiện sinh học)

A	B	¬ (A ∨ B)	[(¬ A) ∧ (¬ B)]	[¬ (A ∨ B)] ⇔ [(¬ A) ∧ (¬ B)]
Thật	Thật	Sai	Sai	Thật
Thật	Sai	Sai	Sai	Thật
Sai	Thật	Sai	Sai	Thật
Sai	Sai	Thật	Thật	Thật

Như $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ là một thuật ngữ tautology, các câu lệnh là tương đương nhau.

Ngược lại, Ngược lại và Ngược lại dương tính

Hàm ý / nếu-thì $(\rightarrow)$còn được gọi là câu lệnh điều kiện. Nó có hai phần -

• Giả thuyết, tr
• Kết luận, q

Như đã đề cập trước đó, nó được ký hiệu là $p \rightarrow q$.

Example of Conditional Statement- "Nếu bạn làm bài tập về nhà của bạn, bạn sẽ không bị phạt." Ở đây, "bạn làm bài tập về nhà" là giả thuyết, p, và "bạn sẽ không bị trừng phạt" là kết luận, q.

Inverse- Một câu lệnh điều kiện nghịch đảo là sự phủ định của cả giả thuyết và kết luận. Nếu câu lệnh là “Nếu p thì q”, thì nghịch đảo sẽ là “Nếu không p thì không phải q”. Do đó, nghịch đảo của$p \rightarrow q$ Là $ \lnot p \rightarrow \lnot q$.

Example - Ngược lại của “Nếu bạn làm bài tập về nhà, bạn sẽ không bị phạt” là “Nếu bạn không làm bài tập về nhà, bạn sẽ bị phạt”.

Converse- Ngược lại của câu điều kiện được tính bằng cách hoán đổi giữa giả thuyết và kết luận. Nếu câu lệnh là “If p, then q”, ngược lại sẽ là “If q, then p”. Trò chuyện của$p \rightarrow q$ Là $q \rightarrow p$.

Example - Câu chuyện của "Nếu bạn làm bài tập của bạn, bạn sẽ không bị phạt" là "Nếu bạn không bị phạt, bạn sẽ làm bài tập về nhà của mình".

Contra-positive- Ngược lại dương của điều kiện được tính bằng cách hoán đổi giữa giả thuyết và kết luận của phát biểu nghịch đảo. Nếu câu lệnh là "Nếu p, thì q", ngược lại dương sẽ là "Nếu không phải q, thì không phải p". Mặt trái tích cực của$p \rightarrow q$ Là $\lnot q \rightarrow \lnot p$.

Example - Mặt trái tích cực của “Nếu bạn làm bài tập về nhà, bạn sẽ không bị phạt” là “Nếu bạn bị phạt, bạn đã không làm bài tập về nhà”.

Nguyên tắc đối ngẫu

Nguyên tắc đối ngẫu phát biểu rằng đối với bất kỳ phát biểu đúng nào, phát biểu đối ngẫu thu được bằng cách hoán đổi các hợp nhất thành các giao điểm (và ngược lại) và hoán đổi tập hợp Phổ thành tập Null (và ngược lại) cũng đúng. Nếu kép của bất kỳ câu lệnh nào là chính câu lệnh đó, nó được cho làself-dual tuyên bố.

Example - Bộ đôi của $(A \cap B ) \cup C$ Là $(A \cup B) \cap C$

Dạng bình thường

Chúng ta có thể chuyển đổi bất kỳ mệnh đề nào ở hai dạng bình thường -

• Dạng chuẩn liên kết
• Hình thức bình thường khó hiểu

Dạng chuẩn liên kết

Một câu lệnh ghép ở dạng chuẩn liên hợp nếu nó có được bằng cách vận hành AND giữa các biến (phủ định của các biến được bao gồm) được kết nối với OR. Về phương diện hoạt động tập hợp, nó là một câu lệnh ghép thu được bởi Giao điểm giữa các biến được kết nối với Unions.

Examples

• $(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$

• $(P \cup Q) \cap (Q \cup R)$

Hình thức thông thường Disjunctive

Một câu lệnh ghép ở dạng chuẩn tắc nếu nó được lấy bằng phép toán OR giữa các biến (phủ định của các biến được bao gồm) được kết nối với AND. Về mặt hoạt động tập hợp, nó là một câu lệnh ghép được Union thu được giữa các biến được kết nối với Giao điểm.

Examples

• $(A \land B) \lor (A \land C) \lor (B \land C \land D)$

• $(P \cap Q) \cup (Q \cap R)$

Predicate Logic xử lý các vị từ, là các mệnh đề có chứa các biến.

Logic vị từ - Định nghĩa

Vị từ là một biểu thức của một hoặc nhiều biến được xác định trên một số miền cụ thể. Một vị từ với các biến có thể được tạo thành một mệnh đề bằng cách gán giá trị cho biến hoặc bằng cách định lượng biến.

Sau đây là một số ví dụ về vị từ -

• Gọi E (x, y) biểu thị "x = y"
• Gọi X (a, b, c) là "a + b + c = 0"
• Gọi M (x, y) là "x kết hôn với y"

Công thức được hình thành tốt

Công thức Well Formed (wff) là một vị từ chứa bất kỳ điều nào sau đây:

• Tất cả các hằng số mệnh đề và các biến mệnh đề đều là wffs

• Nếu x là một biến và Y là một biến, $\forall x Y$ và $\exists x Y$ cũng wff

• Giá trị true và giá trị sai là wffs

• Mỗi công thức nguyên tử là một wff

• Tất cả các kết nối kết nối wffs là wffs

Bộ định lượng

Biến của vị từ được định lượng bằng các bộ định lượng. Có hai loại định lượng trong logic vị từ - Định lượng phổ quát và Định lượng hiện sinh.

Bộ định lượng phổ quát

Bộ định lượng phổ quát tuyên bố rằng các tuyên bố trong phạm vi của nó đúng với mọi giá trị của biến cụ thể. Nó được biểu thị bằng ký hiệu$\forall$.

$\forall x P(x)$ được đọc là với mọi giá trị của x, P (x) là true.

Example - "Con người là phàm nhân" có thể được chuyển thành dạng mệnh đề $\forall x P(x)$ trong đó P (x) là vị từ biểu thị x là người phàm và vũ trụ của diễn ngôn là tất cả đàn ông.

Bộ định lượng hiện tại

Bộ định lượng tồn tại tuyên bố rằng các câu lệnh trong phạm vi của nó đúng với một số giá trị của biến cụ thể. Nó được biểu thị bằng ký hiệu$\exists $.

$\exists x P(x)$ được đọc như đối với một số giá trị của x, P (x) là true.

Example - "Một số người không trung thực" có thể được chuyển thành dạng mệnh đề $\exists x P(x)$ trong đó P (x) là vị từ biểu thị x là không trung thực và vũ trụ của diễn ngôn là một số người.

Bộ định lượng lồng nhau

Nếu chúng ta sử dụng một bộ định lượng xuất hiện trong phạm vi của một bộ định lượng khác, nó được gọi là bộ định lượng lồng nhau.

Example

• $\forall\ a\: \exists b\: P (x, y)$ Ở đâu $P (a, b)$ biểu thị $a + b = 0$

• $\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ Ở đâu $P (a, b)$ biểu thị $a + (b + c) = (a + b) + c$

Note - $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$

Để suy ra những tuyên bố mới từ những tuyên bố có sự thật mà chúng ta đã biết, Rules of Inference được sử dụng.

Quy tắc suy luận để làm gì?

Lôgic toán học thường được sử dụng để chứng minh lôgic. Chứng minh là những lập luận xác đáng xác định giá trị chân lý của các phát biểu toán học.

Một đối số là một chuỗi các câu lệnh. Phát biểu cuối cùng là kết luận và tất cả các phát biểu trước nó được gọi là tiền đề (hoặc giả thuyết). Biểu tượng "$\therefore$”, (Đọc do đó) được đặt trước phần kết luận. Một lập luận hợp lệ là một trong đó kết luận được đưa ra từ các giá trị chân lý của tiền đề.

Quy tắc Suy luận cung cấp các mẫu hoặc hướng dẫn để xây dựng các đối số hợp lệ từ các câu lệnh mà chúng tôi đã có.

Bảng quy tắc suy luận

Quy tắc suy luận	Tên	Quy tắc suy luận	Tên
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$	Thêm vào	$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$	Chủ nghĩa âm tiết không hợp lý
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$	Kết hợp	$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$	Thuyết âm tiết giả thuyết
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$	Đơn giản hóa	$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$	Tiến thoái lưỡng nan về xây dựng
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$	Modus Ponens	$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$	Thế tiến thoái lưỡng nan hủy diệt
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$	Modus Tollens

Thêm vào

Nếu P là tiền đề, chúng ta có thể sử dụng quy tắc cộng để suy ra $ P \lor Q $.

$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$

Thí dụ

Đặt P là mệnh đề, “Anh ấy học rất chăm chỉ” là đúng

Do đó - "Hoặc là anh ấy học rất chăm chỉ Hoặc anh ấy là một học sinh rất tệ." Ở đây Q là mệnh đề “anh ấy là một học sinh rất tệ”.

Kết hợp

Nếu P và Q là hai tiền đề, chúng ta có thể sử dụng quy tắc Kết hợp để suy ra $ P \land Q $.

$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$

Thí dụ

Hãy để P - "Anh ấy học rất chăm chỉ"

Hãy để Q - "Anh ấy là cậu bé giỏi nhất trong lớp"

Vì vậy - "Anh ấy học rất chăm chỉ và là cậu bé học giỏi nhất lớp"

Đơn giản hóa

Nếu $P \land Q$ là tiền đề, chúng ta có thể sử dụng quy tắc đơn giản hóa để suy ra P.

$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$

Thí dụ

"Cậu ấy học rất chăm chỉ và là cậu bé giỏi nhất lớp", $P \land Q$

Do đó - "Anh ấy học rất chăm chỉ"

Modus Ponens

Nếu P và $P \rightarrow Q$ là hai tiền đề, chúng ta có thể sử dụng Modus Ponens để suy ra Q.

$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$

Thí dụ

"Có mật khẩu thì đăng nhập facebook", $P \rightarrow Q$

"Bạn có một mật khẩu", P

Do đó - "Bạn có thể đăng nhập vào facebook"

Modus Tollens

Nếu $P \rightarrow Q$ và $\lnot Q$ là hai tiền đề, chúng ta có thể sử dụng Modus Tollens để suy ra $\lnot P$.

$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$

Thí dụ

"Có mật khẩu thì đăng nhập facebook", $P \rightarrow Q$

"Bạn không thể đăng nhập vào facebook", $\lnot Q$

Do đó - "Bạn không có mật khẩu"

Chủ nghĩa âm tiết không hợp lý

Nếu $\lnot P$ và $P \lor Q$ là hai tiền đề, chúng ta có thể sử dụng Chủ nghĩa âm tiết không kết hợp để suy ra Q.

$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$

Thí dụ

"Kem không có hương vani", $\lnot P$

"Kem có vị vani hoặc vị sô cô la", $P \lor Q$

Do đó - "Kem có vị sô cô la"

Thuyết âm tiết giả thuyết

Nếu $P \rightarrow Q$ và $Q \rightarrow R$ là hai tiền đề, chúng ta có thể sử dụng Thuyết âm tiết giả thuyết để suy ra $P \rightarrow R$

$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$

Thí dụ

"Nếu trời mưa, tôi sẽ không đi học", $P \rightarrow Q$

"Nếu tôi không đi học, tôi sẽ không cần làm bài tập về nhà", $Q \rightarrow R$

Do đó - "Nếu trời mưa, tôi sẽ không cần làm bài tập về nhà"

Tiến thoái lưỡng nan về xây dựng

Nếu $( P \rightarrow Q ) \land (R \rightarrow S)$ và $P \lor R$ là hai tiền đề, chúng ta có thể sử dụng tình huống tiến thoái lưỡng nan mang tính xây dựng để suy ra $Q \lor S$.

$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$

Thí dụ

"Nếu trời mưa, tôi sẽ nghỉ phép", $( P \rightarrow Q )$

"Nếu bên ngoài trời nóng, tôi sẽ đi tắm", $(R \rightarrow S)$

"Có thể là trời sẽ mưa hoặc ngoài trời nóng", $P \lor R$

Do đó - "Tôi xin nghỉ phép hoặc tôi sẽ đi tắm"

Thế tiến thoái lưỡng nan hủy diệt

Nếu $(P \rightarrow Q) \land (R \rightarrow S)$ và $ \lnot Q \lor \lnot S $ là hai tiền đề, chúng ta có thể sử dụng tình thế tiến thoái lưỡng nan hủy diệt để tìm ra $\lnot P \lor \lnot R$.

$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$

Thí dụ

"Nếu trời mưa, tôi sẽ nghỉ phép", $(P \rightarrow Q )$

"Nếu bên ngoài trời nóng, tôi sẽ đi tắm", $(R \rightarrow S)$

"Hoặc tôi sẽ không nghỉ phép hoặc tôi sẽ không đi tắm", $\lnot Q \lor \lnot S$

Do đó - "Trời không mưa hoặc ngoài trời không nóng"

Lý thuyết Nhóm là một nhánh của toán học và đại số trừu tượng xác định một cấu trúc đại số có tên là group. Nói chung, một nhóm bao gồm một tập hợp các phần tử và một phép toán trên hai phần tử bất kỳ trên tập hợp đó để tạo thành một phần tử thứ ba cũng trong tập hợp đó.

Năm 1854, Arthur Cayley, nhà toán học người Anh, lần đầu tiên đưa ra định nghĩa hiện đại về nhóm -

“A set of symbols all of them different, and such that the product of any two of them (no matter in what order), or the product of any one of them into itself, belongs to the set, is said to be a group. These symbols are not in general convertible [commutative], but are associative.”

In this chapter, we will know about operators and postulates that form the basics of set theory, group theory and Boolean algebra.

Any set of elements in a mathematical system may be defined with a set of operators and a number of postulates.

A binary operator defined on a set of elements is a rule that assigns to each pair of elements a unique element from that set. For example, given the set $ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, we can say $\otimes$ is a binary operator for the operation $c = a \otimes b$, if it specifies a rule for finding c for the pair of $(a,b)$, such that $a,b,c \in A$.

The postulates of a mathematical system form the basic assumptions from which rules can be deduced. The postulates are −

Closure

A set is closed with respect to a binary operator if for every pair of elements in the set, the operator finds a unique element from that set.

Example

Let $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$

This set is closed under binary operator into $(\ast)$, because for the operation $c = a \ast b$, for any $a, b \in A$, the product $c \in A$.

The set is not closed under binary operator divide $(\div)$, because, for the operation $c = a \div b$, for any $a, b \in A$, the product c may not be in the set A. If $a = 7, b = 2$, then $c = 3.5$. Here $a,b \in A$ but $c \notin A$.

Associative Laws

A binary operator $\otimes$ on a set A is associative when it holds the following property −

$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, where $x, y, z \in A $

Example

Let $A = \lbrace 1, 2, 3, 4 \rbrace$

The operator plus $( + )$ is associative because for any three elements, $x,y,z \in A$, the property $(x + y) + z = x + ( y + z )$ holds.

The operator minus $( - )$ is not associative since

$$( x - y ) - z \ne x - ( y - z )$$

Commutative Laws

A binary operator $\otimes$ on a set A is commutative when it holds the following property −

$x \otimes y = y \otimes x$, Ở đâu $x, y \in A$

Thí dụ

Để cho $A = \lbrace 1, 2, 3, 4 \rbrace$

Nhà điều hành cộng $( + )$ là giao hoán vì đối với hai phần tử bất kỳ, $x,y \in A$, bất động sản $x + y = y + x$ nắm giữ.

Toán tử trừ $( - )$ không liên quan vì

$$x - y \ne y - x$$

Luật phân tán

Hai toán tử nhị phân $\otimes$ và $\circledast$ trên một tập hợp A, được phân phối trên toán tử $\circledast$ khi tài sản sau giữ -

$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$, Ở đâu $x, y, z \in A $

Thí dụ

Để cho $A = \lbrace 1, 2, 3, 4 \rbrace$

Các nhà khai thác thành $( * )$ và cộng thêm $( + )$ được phân phối trên toán tử + vì đối với ba phần tử bất kỳ, $x,y,z \in A$, bất động sản $x * ( y + z ) = ( x * y ) + ( x * z )$ nắm giữ.

Tuy nhiên, những nhà khai thác này không phân phối $*$ từ

$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$

Yếu tố nhận dạng

Một tập hợp A có một phần tử nhận dạng đối với một phép toán nhị phân $\otimes$ trên A, nếu tồn tại một phần tử $e \in A$, sao cho tài sản sau giữ:

$e \otimes x = x \otimes e$, Ở đâu $x \in A$

Thí dụ

Để cho $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$

Phần tử 1 là phần tử nhận dạng liên quan đến hoạt động $*$ vì đối với bất kỳ phần tử nào $x \in Z$,

$$1 * x = x * 1$$

Mặt khác, không có yếu tố nhận dạng cho hoạt động trừ $( - )$

Nghịch đảo

Nếu một tập hợp A có một phần tử đồng nhất $e$ đối với toán tử nhị phân $\otimes $, nó được cho là có nghịch đảo bất cứ khi nào đối với mọi phần tử $x \in A$, tồn tại một phần tử khác $y \in A$, sao cho tài sản sau giữ:

$$x \otimes y = e$$

Thí dụ

Để cho $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$

Với hoạt động cộng $( + )$ và $e = 0$, nghịch đảo của bất kỳ phần tử x nào là $(-x)$ từ $x + (x) = 0$

Định luật De Morgan

Định luật De Morgan đưa ra một cặp phép biến đổi giữa hợp và giao của hai (hoặc nhiều) tập hợp về mặt bổ sung của chúng. Luật là -

$$(A \cup B)' = A' \cap B'$$

$$(A \cap B)' = A' \cup B'$$

Thí dụ

Để cho $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$và

Bộ phổ quát $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$

$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$

$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$

$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$

$A \cap B = \lbrace 1, 3 \rbrace $

$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$

$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$

Như vậy, chúng ta thấy rằng $(A \cup B)' = A' \cap B'$

$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$

$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$

Như vậy, chúng ta thấy rằng $(A \cap B)' = A' \cup B'$

Semigroup

Một tập hợp hữu hạn hoặc vô hạn $‘S’$ với một phép toán nhị phân $‘\omicron’$ (Thành phần) được gọi là semigroup nếu nó đồng thời tuân theo hai điều kiện:

• Closure - Cho mọi cặp $(a, b) \in S, \:(a \omicron b)$ phải có mặt trong bộ $S$.

• Associative - Đối với mọi yếu tố $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ phải giữ.

Thí dụ

Tập hợp các số nguyên dương (không bao gồm số 0) với phép toán cộng là một nhóm bán phần. Ví dụ,$ S = \lbrace 1, 2, 3, \dots \rbrace $

Ở đây, thuộc tính đóng được giữ như cho mọi cặp $(a, b) \in S, (a + b)$ có mặt trong tập S. Ví dụ, $1 + 2 = 3 \in S]$

Thuộc tính liên kết cũng giữ cho mọi phần tử $a, b, c \in S, (a + b) + c = a + (b + c)$. Ví dụ,$(1 + 2) + 3 = 1 + (2 + 3) = 5$

Monoid

Một monoid là một nhóm bán lẻ có phần tử nhận dạng. Yếu tố nhận dạng (được biểu thị bằng$e$ hoặc E) của tập hợp S là phần tử sao cho $(a \omicron e) = a$, cho mọi phần tử $a \in S$. Yếu tố nhận dạng còn được gọi làunit element. Vì vậy, một monoid có ba thuộc tính đồng thời -Closure, Associative, Identity element.

Thí dụ

Tập hợp các số nguyên dương (không bao gồm số 0) với phép toán nhân là một đơn nguyên. $S = \lbrace 1, 2, 3, \dots \rbrace $

Ở đây, thuộc tính đóng được giữ như cho mọi cặp $(a, b) \in S, (a \times b)$ có mặt trong tập S. [Ví dụ: $1 \times 2 = 2 \in S$ và như thế]

Thuộc tính liên kết cũng giữ cho mọi phần tử $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [Ví dụ, $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ và như thế]

Thuộc tính danh tính cũng giữ cho mọi phần tử $a \in S, (a \times e) = a$ [Ví dụ, $(2 \times 1) = 2, (3 \times 1) = 3$và như thế]. Ở đây yếu tố nhận dạng là 1.

Nhóm

Một nhóm là một đơn nguyên với một phần tử nghịch đảo. Phần tử nghịch đảo (ký hiệu là I) của tập S là phần tử sao cho$(a \omicron I) = (I \omicron a) = a$, cho mỗi phần tử $a \in S$. Vì vậy, một nhóm có bốn thuộc tính đồng thời - i) Đóng, ii) Liên kết, iii) Yếu tố nhận dạng, iv) Yếu tố nghịch đảo. Bậc của một nhóm G là số phần tử trong G và bậc của một phần tử trong một nhóm là số nguyên dương n nhỏ nhất sao cho an là phần tử đồng nhất của nhóm G đó.

Ví dụ

Bộ $N \times N$ các ma trận không số ít tạo thành một nhóm dưới phép toán nhân ma trận.

Sản phẩm của hai $N \times N$ ma trận không số ít cũng là một $N \times N$ ma trận không số ít chứa thuộc tính đóng.

Phép nhân ma trận chính nó là liên kết. Do đó, tài sản liên kết giữ.

Bộ $N \times N$ ma trận không số ít chứa ma trận nhận dạng giữ thuộc tính phần tử nhận dạng.

Vì tất cả các ma trận đều không phải là số ít nên tất cả đều có phần tử nghịch đảo cũng là ma trận không số. Do đó, tài sản nghịch đảo cũng được giữ.

Abelian Group

Nhóm abelian G là nhóm mà cặp nguyên tố $(a,b) \in G$luôn giữ luật giao hoán. Vì vậy, một nhóm nắm giữ đồng thời năm thuộc tính - i) Đóng, ii) Liên kết, iii) Yếu tố nhận dạng, iv) Yếu tố nghịch đảo, v) Giao hoán.

Thí dụ

Tập hợp các số nguyên dương (bao gồm cả số 0) với phép toán cộng là một nhóm abel. $G = \lbrace 0, 1, 2, 3, \dots \rbrace$

Ở đây, thuộc tính đóng được giữ như cho mọi cặp $(a, b) \in S, (a + b)$ có mặt trong tập S. [Ví dụ: $1 + 2 = 2 \in S$ và như thế]

Thuộc tính liên kết cũng giữ cho mọi phần tử $a, b, c \in S, (a + b) + c = a + (b + c)$ [Ví dụ, $(1 +2) + 3 = 1 + (2 + 3) = 6$ và như thế]

Thuộc tính danh tính cũng giữ cho mọi phần tử $a \in S, (a \times e) = a$ [Ví dụ, $(2 \times 1) = 2, (3 \times 1) = 3$và như thế]. Ở đây, yếu tố nhận dạng là 1.

Thuộc tính giao hoán cũng giữ cho mọi phần tử $a \in S, (a \times b) = (b \times a)$ [Ví dụ, $(2 \times 3) = (3 \times 2) = 3$ và như thế]

Nhóm tuần hoàn và nhóm con

A cyclic grouplà một nhóm có thể được tạo bởi một phần tử duy nhất. Mỗi phần tử của một nhóm tuần hoàn là công suất của một phần tử cụ thể nào đó được gọi là máy phát. Một nhóm tuần hoàn có thể được tạo ra bởi bộ tạo 'g', sao cho mọi phần tử khác của nhóm có thể được viết dưới dạng công suất của bộ tạo 'g'.

Thí dụ

Tập hợp các số phức $\lbrace 1,-1, i, -i \rbrace$ dưới phép toán nhân là một nhóm tuần hoàn.

Có hai máy phát điện - $i$ và $–i$ như $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ và cả $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$trong đó bao gồm tất cả các yếu tố của nhóm. Do đó, nó là một nhóm tuần hoàn.

Note - A cyclic groupluôn là nhóm abel nhưng không phải mọi nhóm abel đều là nhóm tuần hoàn. Các số hữu tỉ trong phép cộng không phải là chu kỳ mà là số abel.

A subgroup H là tập con của nhóm G (ký hiệu là $H ≤ G$) nếu nó thỏa mãn đồng thời bốn thuộc tính - Closure, Associative, Identity elementvà Inverse.

Một nhóm con H của một nhóm G không bao gồm cả nhóm G được gọi là một nhóm con thích hợp (Ký hiệu bởi $H < G$). Một nhóm con của một nhóm cyclic là tuần hoàn và một nhóm con abelian cũng là abelian.

Thí dụ

Hãy để một nhóm $G = \lbrace 1, i, -1, -i \rbrace$

Sau đó, một số nhóm con là $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,

Đây không phải là một nhóm con - $H_3 = \lbrace 1, i \rbrace$ bởi vì $(i)^{-1} = -i$ không có trong $H_3$

Bộ có thứ tự một phần (POSET)

Tập hợp có thứ tự một phần bao gồm một tập hợp có quan hệ nhị phân phản xạ, phản đối xứng và bắc cầu. "Bộ có thứ tự từng phần" được viết tắt là POSET.

Ví dụ

• Tập hợp các số thực trong phép toán nhị phân nhỏ hơn hoặc bằng $(\le)$ là một poset.

  Để bộ $S = \lbrace 1, 2, 3 \rbrace$ và hoạt động là $\le$

  Các mối quan hệ sẽ $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$

  Mối quan hệ R này có tính phản xạ là $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$

  Mối quan hệ R này là phản đối xứng, như

  $\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$

  Mối quan hệ R này cũng có tính bắc cầu như $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$.

  Do đó, nó là một poset.

• Tập đỉnh của đồ thị xoay chiều có hướng trong phép toán 'khả năng truy cập' là một tập hợp.

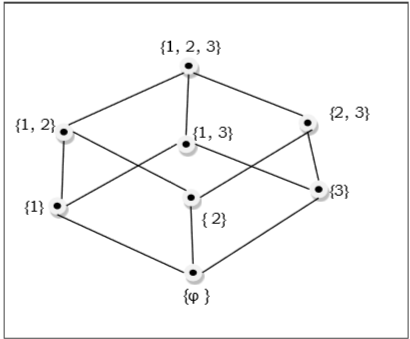
Sơ đồ Hasse

Biểu đồ Hasse của poset là đồ thị có hướng mà các đỉnh là phần tử của poset đó và các cung bao trùm các cặp (x, y) trong poset. Nếu ở vị trí$x < y$, khi đó điểm x xuất hiện thấp hơn điểm y trong biểu đồ Hasse. Nếu$x<y<z$ trong poset, thì mũi tên không được hiển thị giữa x và z vì nó là ẩn.

Thí dụ

Tập hợp các tập con của $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ được hiển thị bằng sơ đồ Hasse sau:

Bộ có thứ tự tuyến tính

Tập hợp có thứ tự tuyến tính hay Tập hợp có thứ tự tổng cộng là một tập hợp thứ tự từng phần trong đó mọi cặp phần tử đều có thể so sánh được. Các yếu tố$a, b \in S$ được cho là có thể so sánh được nếu $a \le b$ hoặc là $b \le a$nắm giữ. Luật tam giác xác định tổng bộ có thứ tự này. Một tập hợp có thứ tự hoàn toàn có thể được định nghĩa là một mạng tinh thể phân phối có thuộc tính$\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ với mọi giá trị của a và b trong tập S.

Thí dụ

Bộ quyền hạn của $\lbrace a, b \rbrace$ sắp xếp theo \ subseteq là một tập hợp có thứ tự hoàn toàn như tất cả các phần tử của tập hợp lũy thừa $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ có thể so sánh được.

Ví dụ về tập hợp đơn hàng không tổng

Một bộ $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ dưới phép toán x chia y không phải là một tập hợp có thứ tự tổng thể.

Đây, cho tất cả $(x, y) \in S, x | y$phải giữ nhưng không đúng là 2 | 3, vì 2 không chia 3 hoặc 3 không chia 2. Do đó, nó không phải là một tập hợp có thứ tự tổng thể.

Mạng lưới

Mạng tinh thể là một poset $(L, \le)$ mà mọi cặp $\lbrace a, b \rbrace \in L$ có giới hạn trên ít nhất (biểu thị bằng $a \lor b$) và giới hạn dưới lớn nhất (được biểu thị bằng $a \land b$). LUB$(\lbrace a,b \rbrace)$được gọi là phép nối của a và b. GLB$(\lbrace a,b \rbrace )$ được gọi là điểm gặp nhau của a và b.

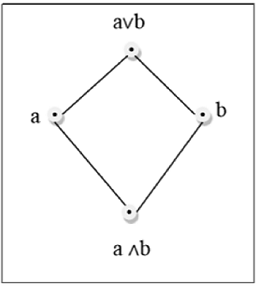
Thí dụ

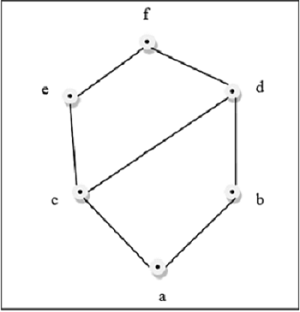
Hình trên là một mạng tinh thể vì đối với mọi cặp $\lbrace a, b \rbrace \in L$, tồn tại một GLB và một LUB.

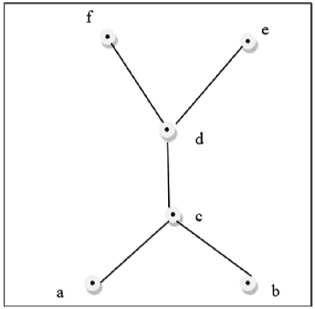
Hình trên không phải là một mạng tinh thể vì $GLB (a, b)$ và $LUB (e, f)$ không tồn tại.

Một số mạng khác được thảo luận dưới đây:

Mạng lưới

Một mạng tinh thể L trở thành mạng có giới hạn nếu nó có phần tử lớn nhất là 1 và phần tử nhỏ nhất là 0.

Mạng lưới bổ sung

Một mạng tinh thể L trở thành một mạng bổ sung nếu nó là một mạng liên kết và nếu mọi phần tử trong mạng có một phần bù. Phần tử x có phần bù x 'nếu$\exists x(x \land x’=0 and x \lor x’ = 1)$

Mạng lưới phân tán

Nếu một mạng tinh thể thỏa mãn hai tính chất phân phối sau đây, nó được gọi là mạng tinh thể phân phối.

• $a \lor (b \land c) = (a \lor b) \land (a \lor c)$

• $a \land (b \lor c) = (a \land b) \lor (a \land c)$

Mạng mô-đun

Nếu một mạng tinh thể thỏa mãn tính chất sau, nó được gọi là mạng tinh thể mô-đun.

$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$

Thuộc tính của lưới

Thuộc tính Idempotent

• $a \lor a = a$

• $a \land a = a$

Tính chất hấp thụ

• $a \lor (a \land b) = a$

• $a \land (a \lor b) = a$

Thuộc tính giao hoán

• $a \lor b = b \lor a$

• $a \land b = b \land a$

Thuộc tính liên kết

• $a \lor (b \lor c) = (a \lor b) \lor c$

• $a \land (b \land c) = (a \land b) \land c$

Kép của một mạng lưới

Đối ngẫu của một mạng tinh thể thu được bằng cách hoán đổi vị trí '$\lor$'và'$\land$'hoạt động.

Thí dụ

Bộ đôi của $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$

Trong cuộc sống hàng ngày, nhiều khi người ta cần tìm ra số lượng tất cả các kết quả có thể xảy ra cho một loạt các sự kiện. Ví dụ, trong số 50 nam và 38 nữ có thể chọn một ban giám khảo gồm 6 nam và 4 nữ bằng bao nhiêu cách? Có thể tạo ra bao nhiêu số PAN gồm 10 chữ cái khác nhau sao cho năm chữ cái đầu tiên là bảng chữ cái viết hoa, bốn chữ số tiếp theo là chữ số và chữ cái cuối cùng là chữ cái viết hoa. Để giải quyết những vấn đề này, lý thuyết toán học về số đếm được sử dụng.Counting chủ yếu bao gồm quy tắc đếm cơ bản, quy tắc hoán vị và quy tắc kết hợp.

Quy tắc Tổng và Sản phẩm

Các Rule of Sum và Rule of Product được sử dụng để phân rã các bài toán đếm khó thành các bài toán đơn giản.

• The Rule of Sum - Nếu một chuỗi các nhiệm vụ $T_1, T_2, \dots, T_m$ có thể được thực hiện trong $w_1, w_2, \dots w_m$ các cách tương ứng (điều kiện là không có tác vụ nào có thể được thực hiện đồng thời), thì số cách để thực hiện một trong các tác vụ này là $w_1 + w_2 + \dots +w_m$. Nếu chúng ta coi hai nhiệm vụ A và B là rời rạc (tức là$A \cap B = \emptyset$), sau đó về mặt toán học $|A \cup B| = |A| + |B|$

• The Rule of Product - Nếu một chuỗi các nhiệm vụ $T_1, T_2, \dots, T_m$ có thể được thực hiện trong $w_1, w_2, \dots w_m$ các cách tương ứng và mọi nhiệm vụ đến sau sự xuất hiện của nhiệm vụ trước đó, sau đó có $w_1 \times w_2 \times \dots \times w_m$cách thực hiện các nhiệm vụ. Về mặt toán học, nếu một nhiệm vụ B đến sau một nhiệm vụ A, thì$|A \times B| = |A|\times|B|$

Thí dụ

Question- Một cậu bé sống ở X và muốn đến Trường ở Z. Từ nhà của cậu ấy, cậu ấy phải đến Y trước rồi đến Y đến Z. Cậu ấy có thể đi X đến Y bằng 3 tuyến xe buýt hoặc 2 tuyến đường tàu. Từ đó, người đó có thể chọn 4 tuyến xe buýt hoặc 5 tuyến xe lửa để đến Z. Có bao nhiêu cách đi từ X đến Z?

Solution - Từ X đến Y, anh ấy có thể đi vào $3 + 2 = 5$cách (Quy tắc tổng). Sau đó, anh ta có thể đi từ Y đến Z trong$4 + 5 = 9$cách (Quy tắc tổng). Do đó từ X đến Z anh ta có thể đi vào$5 \times 9 = 45$ cách (Quy tắc của Sản phẩm).

Hoán vị

A permutationlà sự sắp xếp của một số yếu tố theo thứ tự quan trọng. Nói cách khác, Hoán vị là một Tổ hợp có thứ tự của các phần tử.

Ví dụ

• Từ một tập hợp S = {x, y, z} bằng cách lấy hai lần cùng một lúc, tất cả các hoán vị là -

  $ xy, yx, xz, zx, yz, zy $.

• Chúng ta phải tạo thành một hoán vị của các số có ba chữ số từ một tập hợp các số $S = \lbrace 1, 2, 3 \rbrace$. Các số có ba chữ số khác nhau sẽ được tạo thành khi chúng ta sắp xếp các chữ số. Hoán vị sẽ là = 123, 132, 213, 231, 312, 321

Số lần hoán vị

Số hoán vị của 'n' vật khác nhau lấy 'r' tại một thời điểm được ký hiệu là $n_{P_{r}}$

$$n_{P_{r}} = \frac{n!}{(n - r)!}$$

Ở đâu $n! = 1.2.3. \dots (n - 1).n$

Proof - Để có 'n' phần tử khác nhau.

Có n số cách điền vào vị trí thứ nhất. Sau khi điền vào vị trí đầu tiên (n-1) số phần tử còn lại. Do đó, có (n-1) cách để điền vào vị trí thứ hai. Sau khi điền vào vị trí thứ nhất và thứ hai, (n-2) số phần tử còn lại. Do đó, có (n-2) cách để điền vào vị trí thứ ba. Bây giờ chúng ta có thể tổng quát hóa số cách điền vào vị trí thứ r là [n - (r – 1)] = n – r + 1

Vì vậy, tổng số không có. cách điền từ vị trí đầu tiên đến vị trí thứ r -

$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$

$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$

Vì thế,

$n_{ P_{ r } } = n! / (n-r)!$

Một số công thức quan trọng của hoán vị

• Nếu có n phần tử trong đó$a_1$ giống nhau về một số loại, $a_2$ giống nhau của một loại khác; $a_3$ giống nhau của loại thứ ba, v.v. và $a_r$ là của $r^{th}$ tử tế, ở đâu $(a_1 + a_2 + ... a_r) = n$.

  Khi đó, số hoán vị của n đối tượng này là = $n! / [(a_1!(a_2!) \dots (a_r!)]$.

• Số hoán vị của n phần tử phân biệt lấy n phần tử tại một thời điểm = $n_{P_n} = n!$

• Số hoán vị của n phần tử giống nhau lấy r phần tử tại một thời điểm, khi x vật cụ thể luôn chiếm vị trí xác định = $n-x_{p_{r-x}}$

• Số hoán vị của n phần tử giống nhau khi r vật xác định luôn đi kèm với nhau là - $r! (n−r+1)!$

• Số hoán vị của n phần tử giống nhau khi r vật xác định không bao giờ kết hợp với nhau là - $n!–[r! (n−r+1)!]$

• Số hoán vị vòng của n phần tử khác nhau lấy x phần tử tại thời điểm = $^np_{x}/x$

• Số hoán vị vòng của n thứ khác nhau = $^np_{n}/n$

Một số vấn đề

Problem 1 - Từ một bó gồm 6 thẻ khác nhau, ta có thể hoán vị bao nhiêu cách?

Solution - Vì chúng ta đang lấy 6 lá một lúc từ bộ bài 6 lá, hoán vị sẽ là $^6P_{6} = 6! = 720$

Problem 2 - Các chữ cái của từ 'READER' có thể được sắp xếp theo bao nhiêu cách?

Solution - Có 6 chữ cái từ (2 E, 1 A, 1D và 2R.) Trong từ 'READER'.

Hoán vị sẽ là $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$

Problem 3 - Các chữ cái của từ 'ORANGE' có thể được sắp xếp như thế nào để các phụ âm chỉ chiếm vị trí chẵn?

Solution- Có 3 nguyên âm và 3 phụ âm trong từ 'ORANGE'. Số cách sắp xếp các phụ âm giữa chúng$= ^3P_{3} = 3! = 6$. 3 chỗ trống còn lại sẽ được lấp đầy bởi 3 nguyên âm trong$^3P_{3} = 3! = 6$các cách. Do đó, tổng số hoán vị là$6 \times 6 = 36$

Kết hợp

A combination là lựa chọn của một số phần tử nhất định mà thứ tự không quan trọng.

Số tất cả các kết hợp của n thứ, lấy r tại một thời điểm là -

$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$

Problem 1

Tìm số tập hợp con của tập hợp $\lbrace1, 2, 3, 4, 5, 6\rbrace$ có 3 yếu tố.

Solution

Tổng số của tập hợp là 6 và chúng ta phải chọn 3 phần tử từ tập hợp. Ở đây, thứ tự không quan trọng. Do đó, số lượng tập hợp con sẽ là$^6C_{3} = 20$.

Problem 2

Có 6 nam và 5 nữ trong một phòng. Trong phòng có bao nhiêu cách chọn 3 nam và 2 nữ?

Solution

Số cách chọn 3 nam trong 6 nam là $^6C_{3}$ và số cách chọn 2 nữ trong 5 nữ là $^5C_{2}$

Do đó, tổng số cách là - $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$

Problem 3

Có bao nhiêu cách chọn 3 nhóm 3 học sinh khác nhau trong tổng số 9 học sinh?

Solution

Hãy để chúng tôi đánh số các nhóm là 1, 2 và 3

Để chọn 3 học sinh cho nhóm ^thứ nhất, số cách -$^9C_{3}$

Số cách chọn 3 học sinh cho nhóm ² sau khi chọn nhóm 1 -$^6C_{3}$

Số cách để lựa chọn 3 sinh viên cho 3 ^thứ nhóm sau khi chọn 1 ^st và 2 ^nd nhóm -$^3C_{3}$

Do đó, tổng số cách $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$

Danh tính của Pascal

Bản sắc của Pascal, trước hết bắt nguồn bởi Blaise Pascal trong 17 ^thứ thế kỷ, tiểu bang rằng số cách để chọn các yếu tố k từ n phần tử bằng tổng của số cách để chọn các yếu tố (k-1) từ (n-1) các yếu tố và số cách chọn phần tử từ n-1 phần tử.

Về mặt toán học, với mọi số nguyên dương k và n: $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$

Proof -

$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$

$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$

$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$

$= (n-1)! \frac{ n } { k!(n-k)! }$

$= \frac{ n! } { k!(n-k)! }$

$= n_{ C_{ k } }$

Nguyên tắc chuồng bồ câu

Năm 1834, nhà toán học người Đức, Peter Gustav Lejeune Dirichlet, đã phát biểu một nguyên tắc mà ông gọi là nguyên tắc ngăn kéo. Bây giờ, nó được gọi là nguyên tắc chuồng bồ câu.

Pigeonhole Principlequy định rằng nếu có ít lỗ chim bồ câu hơn tổng số chim bồ câu và mỗi con chim bồ câu được bỏ vào một lỗ chim bồ câu thì phải có ít nhất một lỗ nuôi chim bồ câu có nhiều hơn một con chim bồ câu. Nếu bỏ n con chim bồ câu vào m ổ chim bồ câu có n> m thì sẽ có một lỗ có nhiều hơn một con chim bồ câu.

Ví dụ

• Mười người đàn ông ở trong một căn phòng và họ bắt tay nhau. Nếu mỗi người bắt tay ít nhất một lần và không người nào bắt tay người đó nhiều hơn một lần thì hai người bắt tay với số lượng như nhau.

• Phải có ít nhất hai người trong một lớp gồm 30 người có tên bắt đầu bằng cùng một bảng chữ cái.

Nguyên tắc Bao gồm-Loại trừ

Các Inclusion-exclusion principletính toán số thứ tự của sự kết hợp của nhiều tập hợp không rời rạc. Đối với hai tập hợp A và B, nguyên tắc phát biểu:

$|A \cup B| = |A| + |B| - |A \cap B|$

Đối với ba tập hợp A, B và C, nguyên tắc phát biểu:

$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$

Công thức tổng quát -

$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\pi-1}|A_1 \cap \dots \cap A_2|$

Problem 1

Có bao nhiêu số nguyên từ 1 đến 50 là bội của 2 hoặc 3 mà không phải là cả hai?

Solution

Từ 1 đến 100, có $50/2 = 25$ các số là bội số của 2.

Có $50/3 = 16$ các số là bội số của 3.

Có $50/6 = 8$ các số là bội của cả 2 và 3.

Vì thế, $|A|=25$, $|B|=16$ và $|A \cap B|= 8$.

$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$

Problem 2

Trong một nhóm gồm 50 sinh viên, 24 sinh viên thích đồ uống lạnh và 36 người thích đồ uống nóng và mỗi sinh viên thích ít nhất một trong hai loại đồ uống. Có bao nhiêu người thích cả cà phê và trà?

Solution

Gọi X là tập hợp những sinh viên thích đồ uống lạnh và Y là tập hợp những người thích đồ uống nóng.

Vì thế, $| X \cup Y | = 50$, $|X| = 24$, $|Y| = 36$

$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$

Do đó, có 10 sinh viên thích cả trà và cà phê.

Liên quan chặt chẽ đến các khái niệm đếm là Xác suất. Chúng tôi thường cố gắng đoán kết quả của các trò chơi may rủi, như trò chơi đánh bài, máy đánh bạc và xổ số; tức là chúng tôi cố gắng tìm khả năng xảy ra hoặc xác suất mà một kết quả cụ thể có được.

Probabilitycó thể được khái niệm hóa như việc tìm kiếm cơ hội xuất hiện của một sự kiện. Về mặt toán học, đó là nghiên cứu các quá trình ngẫu nhiên và kết quả của chúng. Các định luật xác suất có khả năng ứng dụng rộng rãi trong nhiều lĩnh vực như di truyền học, dự báo thời tiết, thăm dò dư luận, thị trường chứng khoán, v.v.

Các khái niệm cơ bản

Lý thuyết xác suất được phát minh vào thế kỷ 17 bởi hai nhà toán học người Pháp, Blaise Pascal và Pierre de Fermat, những người đang giải quyết các vấn đề toán học liên quan đến may rủi.

Trước khi tiếp tục chi tiết về xác suất, chúng ta hãy tìm hiểu khái niệm về một số định nghĩa.

Random Experiment- Một thử nghiệm trong đó tất cả các kết quả có thể xảy ra và không thể dự đoán trước kết quả chính xác được gọi là thử nghiệm ngẫu nhiên. Tung đồng xu công bằng là một ví dụ về thử nghiệm ngẫu nhiên.

Sample Space- Khi chúng ta thực hiện một thí nghiệm, thì tập hợp S của tất cả các kết quả có thể xảy ra được gọi là không gian mẫu. Nếu chúng ta tung đồng xu, không gian mẫu$S = \left \{ H, T \right \}$

Event- Một tập con bất kỳ của không gian mẫu được gọi là biến cố. Sau khi tung đồng xu, nhận được Trụ trên đỉnh là một sự kiện.

Từ "xác suất" có nghĩa là cơ hội xảy ra của một sự kiện cụ thể. Điều tốt nhất chúng ta có thể nói là khả năng xảy ra của chúng, bằng cách sử dụng ý tưởng về xác suất.

$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$

Vì sự xuất hiện của bất kỳ sự kiện nào thay đổi trong khoảng từ 0% đến 100%, xác suất thay đổi từ 0 đến 1.

Các bước để tìm xác suất

Bước 1 - Tính toán tất cả các kết quả có thể có của thử nghiệm.

Bước 2 - Tính số lượng kết quả thuận lợi của thí nghiệm.

Bước 3 - Áp dụng công thức xác suất tương ứng.

Tung đồng xu

Nếu một đồng xu được tung, có hai kết quả có thể xảy ra - Người đứng đầu $(H)$ hoặc Tails $(T)$

Vì vậy, Tổng số kết quả = 2

Do đó, xác suất nhận được Đầu $(H)$ trên cùng là 1/2 và xác suất nhận được Vỹ $(T)$ trên cùng là 1/2

Ném xúc xắc

Khi ném một con xúc xắc, sáu kết quả có thể xảy ra có thể ở trên cùng - $1, 2, 3, 4, 5, 6$.

Xác suất của bất kỳ một trong các số là 1/6

Xác suất lấy được số chẵn là 3/6 = 1/2

Xác suất nhận được số lẻ là 3/6 = 1/2

Lấy thẻ từ một bộ bài

Từ bộ bài 52 lá, nếu một lá được chọn, tìm xác suất rút được quân át và cũng tìm xác suất rút được kim cương.

Tổng số kết quả có thể xảy ra - 52

Kết quả là một át chủ bài - 4

Xác suất trở thành con át chủ bài = 4/52 = 1/13

Xác suất trở thành viên kim cương = 13/52 = 1/4

Tiên đề xác suất

• Xác suất của một sự kiện luôn thay đổi từ 0 đến 1. $[0 \leq P(x) \leq 1]$

• Đối với một sự kiện không thể xảy ra, xác suất là 0 và đối với một sự kiện nhất định, xác suất là 1.

• Nếu sự xuất hiện của một sự kiện này không bị ảnh hưởng bởi sự kiện khác, chúng được gọi là loại trừ lẫn nhau hoặc rời rạc.

  Nếu $A_1, A_2....A_n$ là các sự kiện loại trừ lẫn nhau / rời rạc, sau đó $P(A_i \cap A_j) = \emptyset $ cho $i \ne j$ và $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$

Tính chất của xác suất

• Nếu có hai sự kiện $x$ và $\overline{x}$bổ sung, thì xác suất của sự kiện bổ sung là -

  $$p(\overline{x}) = 1-p(x)$$

• Đối với hai sự kiện không rời rạc A và B, xác suất của sự kết hợp của hai sự kiện -

  $P(A \cup B) = P(A) + P(B)$

• Nếu một sự kiện A là một tập con của một sự kiện B khác (tức là $A \subset B$), thì xác suất của A nhỏ hơn hoặc bằng xác suất của B. Do đó, $A \subset B$ ngụ ý $P(A) \leq p(B)$

Xác suất có điều kiện

Xác suất có điều kiện của sự kiện B là xác suất mà sự kiện sẽ xảy ra khi sự kiện A đã xảy ra. Điều này được viết là$P(B|A)$.

Về mặt toán học - $ P(B|A) = P(A \cap B)/ P(A)$

Nếu sự kiện A và B loại trừ lẫn nhau, thì xác suất có điều kiện của sự kiện B sau sự kiện A sẽ là xác suất của sự kiện B là $P(B)$.

Problem 1

Ở một quốc gia, 50% thanh thiếu niên sở hữu xe đạp và 30% thanh thiếu niên sở hữu xe đạp và đạp xe. Xác suất mà một thiếu niên sở hữu xe đạp cho rằng thiếu niên đó sở hữu một chu kỳ là bao nhiêu?

Solution

Giả sử A là biến cố thanh thiếu niên chỉ sở hữu một chiếc xe đạp và B là biến cố thanh thiếu niên chỉ sở hữu một chiếc xe đạp.

Vì thế, $P(A) = 50/100 = 0.5$ và $P(A \cap B) = 30/100 = 0.3$ từ bài toán đã cho.

$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$

Do đó, xác suất một thiếu niên sở hữu xe đạp cho rằng thiếu niên đó sở hữu một vòng quay là 60%.

Problem 2

Trong một lớp học, 50% học sinh chơi cricket và 25% tổng số học sinh chơi cricket và bóng chuyền. Xác suất để một học sinh chơi bóng chuyền và một học sinh chơi cricket là bao nhiêu?

Solution

Giả sử A là sự kiện học sinh chỉ chơi cricket và B là sự kiện học sinh chỉ chơi bóng chuyền.

Vì thế, $P(A) = 50/100 =0.5$ và $P(A \cap B) = 25/ 100 =0.25$ từ bài toán đã cho.

$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$

Do đó, xác suất một sinh viên chơi bóng chuyền và sinh viên đó chơi cricket là 50%.

Problem 3

Sáu máy tính xách tay tốt và ba máy tính xách tay bị lỗi được trộn lẫn với nhau. Để tìm ra các máy tính xách tay bị lỗi, tất cả chúng đều được kiểm tra ngẫu nhiên từng chiếc một. Xác suất để tìm được cả hai máy tính xách tay bị lỗi trong hai lần chọn đầu tiên là bao nhiêu?

Solution

Gọi A là sự kiện chúng ta tìm thấy một máy tính xách tay bị lỗi trong lần kiểm tra đầu tiên và B là sự kiện chúng ta tìm thấy một máy tính xách tay bị lỗi trong lần kiểm tra thứ hai.

Vì thế, $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$

Định lý Bayes

Theorem - Nếu A và B là hai sự kiện loại trừ lẫn nhau, trong đó $P(A)$ là xác suất của A và $P(B)$ là xác suất của B, $P(A | B)$ là xác suất của A cho rằng B đúng. $P(B | A)$ là xác suất của B cho rằng A đúng, thì Định lý Bayes phát biểu:

$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$

Ứng dụng của Định lý Bayes

• Trong các tình huống mà tất cả các sự kiện của không gian mẫu là các sự kiện loại trừ lẫn nhau.

• Trong những tình huống mà một trong hai $P( A_i \cap B )$ cho mỗi $A_i$ hoặc là $P( A_i )$ và $P(B|A_i)$ cho mỗi $A_i$ đã được biết đến.

Problem

Hãy xem xét ba giá đỡ bút. Giá đựng bút thứ nhất chứa 2 bút đỏ và 3 bút xanh; cái thứ hai có 3 bút đỏ và 2 bút xanh; còn chiếc thứ ba có 4 bút đỏ và 1 bút xanh. Xác suất để chọn mỗi giá đỡ bút là như nhau. Nếu một cây bút được rút ra một cách ngẫu nhiên thì xác suất nó là một cây bút màu đỏ là bao nhiêu?

Solution

Để cho $A_i$là sự kiện mà giá bút ^thứ i được chọn.

Ở đây, i = 1,2,3.

Vì xác suất để chọn một giá đỡ bút là bằng nhau, $P(A_i) = 1/3$

Gọi B là biến cố bút đỏ được vẽ.

Xác suất để một cây bút đỏ được chọn trong số năm cây viết của giá đựng bút thứ nhất,

$P(B|A_1) = 2/5$

Xác suất để một cây bút đỏ được chọn trong số năm cây bút của giá đựng bút thứ hai,

$P(B|A_2) = 3/5$

Xác suất để một cây bút màu đỏ được chọn trong số năm cây bút của giá đựng bút thứ ba,

$P(B|A_3) = 4/5$

Theo Định lý Bayes,

$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$

$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$

$= 3/5$

Mathematical induction, là một kỹ thuật để chứng minh kết quả hoặc thiết lập các câu lệnh cho các số tự nhiên. Phần này minh họa phương pháp thông qua nhiều ví dụ.

Định nghĩa

Mathematical Induction là một kỹ thuật toán học được sử dụng để chứng minh một tuyên bố, một công thức hoặc một định lý là đúng với mọi số tự nhiên.

Kỹ thuật này bao gồm hai bước để chứng minh một tuyên bố, như được nêu dưới đây:

Step 1(Base step) - Nó chứng minh rằng một câu lệnh đúng với giá trị ban đầu.

Step 2(Inductive step)- Điều đó chứng tỏ rằng nếu câu lệnh đúng với ^lần lặp ^thứ n (hoặc số n ) thì nó cũng đúng với ^lần lặp ^thứ (n + 1) (hoặc số n + 1 ).

Làm thế nào để làm nó

Step 1- Xem xét một giá trị ban đầu mà câu lệnh là đúng. Nó được chứng minh rằng câu lệnh đúng với n = giá trị ban đầu.

Step 2- Giả sử câu lệnh đúng với mọi giá trị của n = k . Sau đó chứng minh mệnh đề đúng với n = k + 1 . Chúng ta thực sự chia n = k + 1 thành hai phần, một phần là n = k (đã được chứng minh) và cố gắng chứng minh phần kia.

Vấn đề 1

$3^n-1$ là bội số của 2 cho n = 1, 2, ...

Solution

Step 1 - Đối với $n = 1, 3^1-1 = 3-1 = 2$ là bội số của 2

Step 2 - Hãy để chúng tôi giả sử $3^n-1$ đúng với $n=k$, Vì thế, $3^k -1$ là đúng (Đó là một giả định)

Chúng tôi phải chứng minh rằng $3^{k+1}-1$ cũng là bội số của 2

$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$

Phần đầu tiên $(2 \times 3k)$ chắc chắn là bội số của 2 và phần thứ hai $(3k -1)$ cũng đúng như giả định trước đây của chúng tôi.

Vì thế, $3^{k+1} – 1$ là bội số của 2.

Vì vậy, nó được chứng minh rằng $3^n – 1$ là bội số của 2.

Vấn đề 2

$1 + 3 + 5 + ... + (2n-1) = n^2$ cho $n = 1, 2, \dots $

Solution

Step 1 - Đối với $n=1, 1 = 1^2$Do đó, bước 1 đã thoả mãn.

Step 2 - Hãy giả sử câu nói đúng với $n=k$.

Vì thế, $1 + 3 + 5 + \dots + (2k-1) = k^2$ là đúng (Đó là một giả định)

Chúng tôi phải chứng minh rằng $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ cũng giữ

$1 + 3 + 5 + \dots + (2(k+1) - 1)$

$= 1 + 3 + 5 + \dots + (2k+2 - 1)$

$= 1 + 3 + 5 + \dots + (2k + 1)$

$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$

$= k^2 + (2k + 1)$

$= (k + 1)^2$

Vì thế, $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ giữ thỏa mãn bước 2.

Vì thế, $1 + 3 + 5 + \dots + (2n - 1) = n^2$ được chứng minh.

Vấn đề 3

Chứng minh rằng $(ab)^n = a^nb^n$ đúng với mọi số tự nhiên $n$

Solution

Step 1 - Đối với $n=1, (ab)^1 = a^1b^1 = ab$Do đó, bước 1 đã thoả mãn.

Step 2 - Hãy giả sử câu nói đúng với $n=k$, Vì thế, $(ab)^k = a^kb^k$ is true (Đó là một giả định).

Chúng tôi phải chứng minh rằng $(ab)^{k+1} = a^{k+1}b^{k+1}$ cũng giữ

Được, $(ab)^k = a^k b^k$

Hoặc là, $(ab)^k (ab) = (a^k b^k ) (ab)$ [Nhân cả hai vế với 'ab']

Hoặc là, $(ab)^{k+1} = (aa^k) ( bb^k)$

Hoặc là, $(ab)^{k+1} = (a^{k+1}b^{k+1})$

Do đó, bước 2 đã được chứng minh.

Vì thế, $(ab)^n = a^nb^n$ đúng với mọi số tự nhiên n.

Cảm ứng mạnh

Cảm ứng mạnh là một dạng khác của quy nạp toán học. Thông qua kỹ thuật quy nạp này, chúng ta có thể chứng minh rằng một hàm mệnh đề,$P(n)$ đúng với tất cả các số nguyên dương, $n$, sử dụng các bước sau:

• Step 1(Base step) - Nó chứng minh rằng mệnh đề ban đầu $P(1)$ thật.

• Step 2(Inductive step) - Nó chứng tỏ rằng câu lệnh điều kiện $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ đúng với số nguyên dương $k$.

Trong chương này, chúng ta sẽ thảo luận về cách các kỹ thuật đệ quy có thể lấy ra các chuỗi và được sử dụng để giải các bài toán đếm. Thủ tục tìm các số hạng của một dãy theo cách đệ quy được gọi làrecurrence relation. Chúng tôi nghiên cứu lý thuyết về quan hệ tuần hoàn tuyến tính và các giải pháp của chúng. Cuối cùng, chúng tôi giới thiệu các hàm tạo để giải quyết các quan hệ lặp lại.

Định nghĩa

Quan hệ lặp lại là một phương trình xác định một cách đệ quy một chuỗi trong đó số hạng tiếp theo là hàm của các số hạng trước đó (Biểu thức $F_n$ như một số kết hợp của $F_i$ với $i < n$).

Example - Chuỗi Fibonacci - $F_n = F_{n-1} + F_{n-2}$, Tháp Hà Nội - $F_n = 2F_{n-1} + 1$

Mối quan hệ lặp lại tuyến tính

Phương trình tái hiện tuyến tính bậc k hoặc bậc k là một phương trình tái hiện có dạng $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $($A_n$ là một hằng số và $A_k \neq 0$) trên một dãy số dưới dạng đa thức bậc nhất.

Đây là một số ví dụ về phương trình lặp lại tuyến tính -

Quan hệ lặp lại	Giá trị ban đầu	Các giải pháp
F n = F n-1 + F n-2	a 1 = a 2 = 1	Số Fibonacci
F n = F n-1 + F n-2	a 1 = 1, a 2 = 3	Số Lucas
F n = F n-2 + F n-3	a 1 = a 2 = a 3 = 1	Chuỗi Padovan
F n = 2F n-1 + F n-2	a 1 = 0, a 2 = 1	Pell số

Cách giải quyết mối quan hệ lặp lại tuyến tính

Giả sử, một quan hệ lặp lại tuyến tính hai có thứ tự là - $F_n = AF_{n-1} +BF_{n-2}$ trong đó A và B là các số thực.

Phương trình đặc trưng cho quan hệ lặp lại ở trên là -

$$x^2 - Ax - B = 0$$

Ba trường hợp có thể xảy ra khi tìm ra gốc rễ -

Case 1 - Nếu phương trình này là $(x- x_1)(x- x_1) = 0$ và nó tạo ra hai gốc thực khác biệt $x_1$ và $x_2$, sau đó $F_n = ax_1^n+ bx_2^n$là giải pháp. [Ở đây, a và b là hằng số]

Case 2 - Nếu phương trình này là $(x- x_1)^2 = 0$ và nó tạo ra một gốc thực duy nhất $x_1$, sau đó $F_n = a x_1^n+ bn x_1^n$ là giải pháp.

Case 3 - Nếu phương trình tạo ra hai nghiệm phức phân biệt, $x_1$ và $x_2$ ở dạng cực $x_1 = r \angle \theta$ và $x_2 = r \angle(- \theta)$, sau đó $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ là giải pháp.

Problem 1

Giải quyết mối quan hệ lặp lại $F_n = 5F_{n-1} - 6F_{n-2}$ Ở đâu $F_0 = 1$ và $F_1 = 4$

Solution

Phương trình đặc trưng của quan hệ tái diễn là -

$$x^2 - 5x + 6 = 0,$$

Vì thế, $(x - 3) (x - 2) = 0$

Do đó, rễ là -

$x_1 = 3$ và $x_2 = 2$

Rễ là có thật và khác biệt. Vì vậy, đây là trường hợp 1

Do đó, giải pháp là -

$$F_n = ax_1^n + bx_2^n$$

Đây, $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$

Vì thế,

$1 = F_0 = a3^0 + b2^0 = a+b$

$4 = F_1 = a3^1 + b2^1 = 3a+2b$

Giải hai phương trình này, chúng ta nhận được $ a = 2$ và $b = -1$

Do đó, giải pháp cuối cùng là -

$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$

Problem 2

Giải quyết mối quan hệ lặp lại - $F_n = 10F_{n-1} - 25F_{n-2}$ Ở đâu $F_0 = 3$ và $F_1 = 17$

Solution

Phương trình đặc trưng của quan hệ tái diễn là -

$$ x^2 - 10x -25 = 0$$

Vì thế $(x - 5)^2 = 0$

Do đó, có một gốc thực duy nhất $x_1 = 5$

Vì chỉ có một gốc có giá trị thực duy nhất, nên nó ở dạng trường hợp 2

Do đó, giải pháp là -

$F_n = ax_1^n + bnx_1^n$

$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$

$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$

Giải hai phương trình này, chúng ta nhận được $a = 3$ và $b = 2/5$

Do đó, giải pháp cuối cùng là - $F_n = 3.5^n +( 2/5) .n.2^n $

Problem 3

Giải quyết mối quan hệ lặp lại $F_n = 2F_{n-1} - 2F_{n-2}$ Ở đâu $F_0 = 1$ và $F_1 = 3$

Solution

Phương trình đặc trưng của quan hệ tái diễn là -

$$x^2 -2x -2 = 0$$

Do đó, rễ là -

$x_1 = 1 + i$ và $x_2 = 1 - i$

Ở dạng cực,

$x_1 = r \angle \theta$ và $x_2 = r \angle(- \theta),$ Ở đâu $r = \sqrt 2$ và $\theta = \frac{\pi}{4}$

Rễ là tưởng tượng. Vì vậy, đây là dạng trường hợp 3.

Do đó, giải pháp là -

$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$

$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$

$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$

Giải hai phương trình này chúng ta nhận được $a = 1$ và $b = 2$

Do đó, giải pháp cuối cùng là -

$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$

Mối quan hệ lặp lại không đồng nhất và các giải pháp cụ thể

Một quan hệ lặp lại được gọi là không thuần nhất nếu nó ở dạng

$F_n = AF_{n-1} + BF_{n-2} + f(n)$ Ở đâu $f(n) \ne 0$

Mối quan hệ lặp lại đồng nhất liên quan của nó là $F_n = AF_{n–1} + BF_{n-2}$

Giải pháp $(a_n)$ của một quan hệ lặp lại không thuần nhất có hai phần.

Phần đầu tiên là giải pháp $(a_h)$ của mối quan hệ lặp lại đồng nhất liên quan và phần thứ hai là giải pháp cụ thể $(a_t)$.

$$a_n=a_h+a_t$$

Giải pháp cho phần đầu tiên được thực hiện bằng cách sử dụng các thủ tục đã thảo luận trong phần trước.

Để tìm ra giải pháp cụ thể, chúng tôi tìm một giải pháp dùng thử thích hợp.

Để cho $f(n) = cx^n$; để cho$x^2 = Ax + B$ là phương trình đặc trưng của quan hệ lặp lại thuần nhất được kết hợp và cho $x_1$ và $x_2$ là gốc rễ của nó.

• Nếu $x \ne x_1$ và $x \ne x_2$, sau đó $a_t = Ax^n$

• Nếu $x = x_1$, $x \ne x_2$, sau đó $a_t = Anx^n$

• Nếu $x = x_1 = x_2$, sau đó $a_t = An^2x^n$

Thí dụ

Cho một quan hệ lặp lại không thuần nhất là $F_n = AF_{n–1} + BF_{n-2} + f(n)$ với rễ đặc trưng $x_1 = 2$ và $x_2 = 5$. Các giải pháp thử nghiệm cho các giá trị có thể có khác nhau của$f(n)$ như sau -