Toán học rời rạc - Bộ

Nhà toán học người Đức G. Cantorgiới thiệu khái niệm tập hợp. Ông đã định nghĩa một tập hợp là một tập hợp các đối tượng xác định và có thể phân biệt được lựa chọn bằng các quy tắc hoặc mô tả nhất định.

Setlý thuyết là cơ sở của một số lĩnh vực nghiên cứu khác như lý thuyết đếm, quan hệ, lý thuyết đồ thị và máy trạng thái hữu hạn. Trong chương này, chúng tôi sẽ đề cập đến các khía cạnh khác nhau củaSet Theory.

Đặt - Định nghĩa

Tập hợp là một tập hợp không có thứ tự của các phần tử khác nhau. Một tập hợp có thể được viết rõ ràng bằng cách liệt kê các phần tử của nó bằng cách sử dụng dấu ngoặc vuông. Nếu thứ tự của các phần tử bị thay đổi hoặc bất kỳ phần tử nào của một tập hợp được lặp lại, nó sẽ không tạo ra bất kỳ thay đổi nào trong tập hợp.

Một số ví dụ về bộ

Tập hợp tất cả các số nguyên dương
Tập hợp tất cả các hành tinh trong hệ mặt trời
Một tập hợp tất cả các tiểu bang ở Ấn Độ
Tập hợp tất cả các chữ cái viết thường của bảng chữ cái

Đại diện của một tập hợp

Tập hợp có thể được biểu diễn theo hai cách:

Bảng phân công hoặc dạng bảng
Đặt ký hiệu trình tạo

Bảng phân công hoặc dạng bảng

Tập hợp được biểu diễn bằng cách liệt kê tất cả các phần tử bao gồm nó. Các phần tử được đặt trong dấu ngoặc nhọn và được phân tách bằng dấu phẩy.

Example 1 - Tập hợp các nguyên âm trong bảng chữ cái tiếng Anh, $ A = \ lbrace a, e, i, o, u \ rbrace $

Example 2 - Tập hợp các số lẻ nhỏ hơn 10, $ B = \ lbrace 1,3,5,7,9 \ rbrace $

Đặt ký hiệu trình tạo

Tập hợp được xác định bằng cách chỉ định một thuộc tính mà các phần tử của tập hợp có điểm chung. Tập hợp được mô tả là $ A = \ lbrace x: p (x) \ rbrace $

Example 1 - Tập hợp $ \ lbrace a, e, i, o, u \ rbrace $ được viết là -

$ A = \ lbrace x: \ text {x là một nguyên âm trong bảng chữ cái tiếng Anh} \ rbrace $

Example 2 - Tập hợp $ \ lbrace 1,3,5,7,9 \ rbrace $ được viết là -

$ B = \ lbrace x: 1 \ le x \ lt 10 \ và \ (x \% 2) \ ne 0 \ rbrace $

Nếu một phần tử x là thành viên của bất kỳ tập S nào, thì nó được ký hiệu là $ x \ trong S $ và nếu một phần tử y không phải là thành viên của tập S, nó được ký hiệu là $ y \ notin S $.

Example- Nếu $ S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, 1 \ in S $ nhưng $ 1.5 \ notin S $

Một số bộ quan trọng

N - tập hợp tất cả các số tự nhiên = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $

Z - tập hợp tất cả các số nguyên = $ \ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $

Z⁺ - tập hợp tất cả các số nguyên dương

Q - tập hợp tất cả các số hữu tỉ

R - tập hợp tất cả các số thực

W - tập hợp tất cả các số nguyên

Số lượng của một tập hợp

Tổng số của một tập hợp S, ký hiệu là $ | S | $, là số phần tử của tập hợp đó. Con số này cũng được gọi là số chính. Nếu một tập hợp có vô số phần tử, thì tổng số của nó là $ \ infty $.

Example- $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ dot \ rbrace | = \ infty $

Nếu có hai tập X và Y,

$ | X | = | Y | $ biểu thị hai tập X và Y có cùng một bản số. Nó xảy ra khi số phần tử trong X đúng bằng số phần tử trong Y. Trong trường hợp này, tồn tại một hàm phân tích 'f' từ X đến Y.
$ | X | \ le | Y | $ biểu thị rằng bộ số của X nhỏ hơn hoặc bằng bộ số của Y. Nó xảy ra khi số phần tử trong X nhỏ hơn hoặc bằng Y. Ở đây, tồn tại một hàm bất biến 'f' từ X đến Y.
$ | X | \ lt | Y | $ biểu thị rằng bản số của bộ X nhỏ hơn bản số của bộ Y. Nó xảy ra khi số phần tử trong X ít hơn Y. Ở đây, hàm 'f' từ X đến Y là hàm không xác định nhưng không phải là hàm phân vị.
$ Nếu \ | X | \ le | Y | $ và $ | X | \ ge | Y | $ rồi đến $ | X | = | Y | $. Tập hợp X và Y thường được gọi là tập hợp tương đương.

Các loại bộ

Bộ có thể được phân thành nhiều loại. Một số trong số đó là hữu hạn, vô hạn, tập con, phổ quát, thích hợp, tập đơn, v.v.

Tập hợp hữu hạn

Một tập hợp chứa một số phần tử xác định được gọi là tập hợp hữu hạn.

Example- $ S = \ lbrace x \: | \: x \ in N $ và $ 70 \ gt x \ gt 50 \ rbrace $

Bộ vô hạn

Tập hợp chứa vô số phần tử được gọi là tập hợp vô hạn.

Example- $ S = \ lbrace x \: | \: x \ in N $ và $ x \ gt 10 \ rbrace $

Tập hợp con

Tập hợp X là tập con của tập Y (Được viết là $ X \ subseteq Y $) nếu mọi phần tử của X là phần tử của tập Y.

Example 1- Cho, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ và $ Y = \ lbrace 1, 2 \ rbrace $. Ở đây tập Y là tập con của tập X vì tất cả các phần tử của tập Y đều nằm trong tập X. Do đó, chúng ta có thể viết $ Y \ subseteq X $.

Example 2- Cho, $ X = \ lbrace 1, 2, 3 \ rbrace $ và $ Y = \ lbrace 1, 2, 3 \ rbrace $. Ở đây tập Y là một tập con (Không phải là một tập hợp con thích hợp) của tập X vì tất cả các phần tử của tập Y đều nằm trong tập X. Do đó, chúng ta có thể viết $ Y \ subseteq X $.

Tập số thực

Thuật ngữ "tập hợp con thích hợp" có thể được định nghĩa là "tập hợp con của nhưng không bằng". Tập hợp X là một tập hợp con thích hợp của tập Y (Được viết là $ X \ tập con Y $) nếu mọi phần tử của X là một phần tử của tập Y và $ | X | \ lt | Y | $.

Example- Cho, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ và $ Y = \ lbrace 1, 2 \ rbrace $. Ở đây, hãy đặt $ Y \ tập con X $ vì tất cả các phần tử trong $ Y $ cũng được chứa trong $ X $ và $ X $ có ít nhất một phần tử lớn hơn tập hợp $ Y $.

Bộ phổ quát

Nó là một tập hợp của tất cả các yếu tố trong một ngữ cảnh hoặc ứng dụng cụ thể. Tất cả các tập hợp trong ngữ cảnh hoặc ứng dụng đó về cơ bản là tập hợp con của tập hợp phổ quát này. Tập hợp phổ quát được biểu diễn dưới dạng $ U $.

Example- Chúng ta có thể định nghĩa $ U $ là tập hợp tất cả các loài động vật trên trái đất. Trong trường hợp này, tập hợp tất cả các loài động vật có vú là tập con $ U $, tập hợp tất cả các loài cá là tập con $ U $, tập hợp tất cả các loài côn trùng là tập con $ U $, v.v.

Tập hợp rỗng hoặc tập hợp rỗng

Một tập hợp rỗng không chứa phần tử nào. Nó được ký hiệu là $ \ blankset $. Vì số phần tử trong một tập hợp rỗng là hữu hạn, nên tập hợp rỗng là một tập hợp hữu hạn. Cardinality của tập hợp rỗng hoặc tập hợp rỗng bằng không.

Example- $ S = \ lbrace x \: | \: x \ in N $ và $ 7 \ lt x \ lt 8 \ rbrace = \ blankset $

Bộ Singleton hoặc Bộ đơn vị

Tập hợp đơn hoặc tập đơn vị chỉ chứa một phần tử. Một tập hợp singleton được ký hiệu là $ \ lbrace s \ rbrace $.

Example- $ S = \ lbrace x \: | \: x \ in N, \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ rbrace $

Tập hợp bằng nhau

Nếu hai tập hợp chứa các phần tử giống nhau thì chúng được cho là bằng nhau.

Example - Nếu $ A = \ lbrace 1, 2, 6 \ rbrace $ và $ B = \ lbrace 6, 1, 2 \ rbrace $, chúng bằng nhau vì mọi phần tử của tập A là một phần tử của tập B và mọi phần tử của tập hợp B là một phần tử của tập A.

Bộ tương đương

Nếu các thẻ số của hai tập hợp giống nhau, chúng được gọi là tập hợp tương đương.

Example- Nếu $ A = \ lbrace 1, 2, 6 \ rbrace $ và $ B = \ lbrace 16, 17, 22 \ rbrace $, chúng tương đương vì bản số của A bằng với bản số của B. tức là $ | A | = | B | = 3 đô la

Bộ chồng chéo

Hai tập hợp có ít nhất một phần tử chung được gọi là tập hợp trùng nhau.

Trong trường hợp các bộ chồng chéo -

$ n (A \ cup B) = n (A) + n (B) - n (A \ cap B) $
$ n (A \ cup B) = n (A - B) + n (B - A) + n (A \ cap B) $
$ n (A) = n (A - B) + n (A \ cap B) $
$ n (B) = n (B - A) + n (A \ cap B) $

Example- Cho, $ A = \ lbrace 1, 2, 6 \ rbrace $ và $ B = \ lbrace 6, 12, 42 \ rbrace $. Có một phần tử chung '6', do đó các tập hợp này là các tập hợp chồng chéo.

Bộ rời

Hai tập hợp A và B được gọi là tập rời rạc nếu chúng không có chung một phần tử. Do đó, các bộ rời rạc có các thuộc tính sau:

$ n (A \ cap B) = \ bộ trống $
$ n (A \ cup B) = n (A) + n (B) $

Example - Cho, $ A = \ lbrace 1, 2, 6 \ rbrace $ và $ B = \ lbrace 7, 9, 14 \ rbrace $, không có một phần tử chung nào, do đó các tập hợp này là các tập hợp chồng chéo.

Sơ đồ Venn

Biểu đồ Venn, được phát minh vào năm 1880 bởi John Venn, là một biểu đồ thể hiện tất cả các quan hệ logic có thể có giữa các bộ toán học khác nhau.

Examples

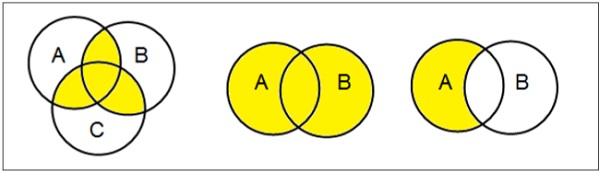
Đặt hoạt động

Các phép toán tập hợp bao gồm Tập hợp liên kết, Giao điểm tập hợp, Sự khác biệt của tập hợp, Bổ sung của tập hợp và Tích Descartes.

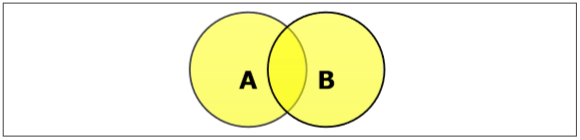
Đặt Liên minh

Tập hợp A và B (ký hiệu là $ A \ cup B $) là tập hợp các phần tử nằm trong A, trong B hoặc trong cả A và B. Do đó, $ A \ cup B = \ lbrace x \: | \: x \ trong A \ HOẶC \ x \ trong B \ rbrace $.

Example- Nếu $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ và B = $ \ lbrace 13, 14, 15 \ rbrace $ thì $ A \ cup B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $. (Phần tử chung chỉ xảy ra một lần)

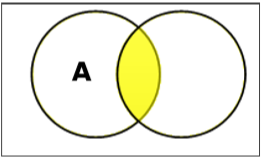
Đặt giao lộ

Giao của tập A và B (ký hiệu là $ A \ cap B $) là tập hợp các phần tử nằm trong cả A và B. Do đó, $ A \ cap B = \ lbrace x \: | \: x \ in A \ VÀ \ x \ trong B \ rbrace $.

Example - Nếu $ A = \ lbrace 11, 12, 13 \ rbrace $ và $ B = \ lbrace 13, 14, 15 \ rbrace $ thì $ A \ cap B = \ lbrace 13 \ rbrace $.

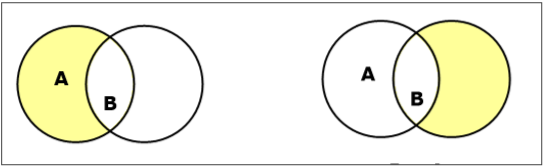
Đặt sự khác biệt / Bổ sung tương đối

Chênh lệch tập hợp của tập A và B (ký hiệu là $ A - B $) là tập các phần tử chỉ thuộc A mà không thuộc B. Do đó, $ A - B = \ lbrace x \: | \: x \ trong A \ AND \ x \ notin B \ rbrace $.

Example- Nếu $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ và $ B = \ lbrace 13, 14, 15 \ rbrace $ thì $ (A - B) = \ lbrace 10, 11, 12 \ rbrace $ và $ (B - A) = \ lbrace 14, 15 \ rbrace $. Tại đây, chúng ta có thể thấy $ (A - B) \ ne (B - A) $

Sự bổ sung của một bộ

Phần bù của tập A (ký hiệu là $ A '$) là tập các phần tử không có trong tập A. Do đó, $ A' = \ lbrace x | x \ notin A \ rbrace $.

Cụ thể hơn, $ A '= (U - A) $ trong đó $ U $ là một tập phổ quát chứa tất cả các đối tượng.

Example- Nếu $ A = \ lbrace x \: | \: x \ \: {thuộc \: thành \: set \: của \: lẻ \: số nguyên} \ rbrace $ thì $ A '= \ lbrace y \: | \: y \: {không \: không \: thuộc \: thành \: bộ \: của \: lẻ \: số nguyên} \ rbrace $

Sản phẩm Descartes / Sản phẩm chéo

Tích Descartes của n số bộ $ A_1, A_2, \ chấm A_n $ được biểu thị là $ A_1 \ lần A_2 \ dấu chấm \ lần A_n $ có thể được xác định là tất cả các cặp có thứ tự $ (x_1, x_2, \ chấm x_n) $ trong đó $ x_1 \ trong A_1, x_2 \ trong A_2, \ chấm x_n \ trong A_n $

Example - Nếu chúng ta lấy hai bộ $ A = \ lbrace a, b \ rbrace $ và $ B = \ lbrace 1, 2 \ rbrace $,

Tích Descartes của A và B được viết là - $ A \ times B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $

Tích Descartes của B và A được viết là - $ B \ times A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $

Bộ nguồn

Tập hợp lũy thừa của một tập S là tập hợp tất cả các tập con của S kể cả tập rỗng. Hệ số của một tập hợp lũy thừa của một tập hợp S có số lượng n là $ 2 ^ n $. Bộ nguồn được ký hiệu là $ P (S) $.

Example −

Đối với một tập hợp $ S = \ lbrace a, b, c, d \ rbrace $, chúng ta hãy tính các tập hợp con -

Tập hợp con có 0 phần tử - $ \ lbrace \ blankset \ rbrace $ (tập hợp trống)
Tập hợp con có 1 phần tử - $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
Tập hợp con có 2 phần tử - $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
Tập hợp con có 3 phần tử - $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
Tập hợp con có 4 phần tử - $ \ lbrace a, b, c, d \ rbrace $

Do đó, $ P (S) = $

$ \ lbrace \ quad \ lbrace \ blankset \ rbrace, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace, \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $

$ | P (S) | = 2 ^ 4 = 16 $

Note - Công suất của một tập hợp rỗng cũng là một tập hợp rỗng.

$ | P (\ lbrace \ blankset \ rbrace) | = 2 ^ 0 = 1 $

Phân vùng của một tập hợp

Phân vùng của một tập hợp, chẳng hạn S , là một tập hợp n tập hợp con rời rạc, giả sử $ P_1, P_2, \ chấm P_n $ thỏa mãn ba điều kiện sau:

$ P_i $ không chứa tập hợp trống.

$ \ lbrack P_i \ ne \ lbrace \ blankset \ rbrace \ cho \ tất cả \ 0 \ lt i \ le n \ rbrack $
Sự kết hợp của các tập hợp con phải bằng toàn bộ tập hợp ban đầu.

$ \ lbrack P_1 \ cup P_2 \ cup \ dot \ cup P_n = S \ rbrack $
Giao của bất kỳ hai tập hợp phân biệt nào là trống.

$ \ lbrack P_a \ cap P_b = \ lbrace \ blankset \ rbrace, \ for \ a \ ne b \ where \ n \ ge a, \: b \ ge 0 \ rbrack $

Example

Cho $ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $

Một phân vùng có thể xảy ra là $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $

Một phân vùng có thể xảy ra khác là $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $