Toán học rời rạc - Quan hệ
Bất cứ khi nào các tập hợp đang được thảo luận, mối quan hệ giữa các phần tử của tập hợp là điều tiếp theo xuất hiện. Relations có thể tồn tại giữa các đối tượng của cùng một tập hợp hoặc giữa các đối tượng của hai hoặc nhiều tập hợp.
Định nghĩa và Thuộc tính
Quan hệ nhị phân R từ tập x đến y (được viết là $ xRy $ hoặc $ R (x, y) $) là một tập con của tích Descartes $ x \ times y $. Nếu cặp thứ tự của G bị đảo ngược, quan hệ cũng thay đổi.
Nói chung quan hệ n-ary R giữa các tập $ A_1, \ dot, \ và \ A_n $ là một tập con của sản phẩm n-ary $ A_1 \ times \ dot \ times A_n $. Số lượng tối thiểu của một quan hệ R là 0 và tối đa là $ n ^ 2 $ trong trường hợp này.
Một quan hệ nhị phân R trên một tập A là một tập con của $ A \ times A $.
Đối với hai tập phân biệt, A và B, có các hồng số tương ứng là m và n , thì tổng số tối đa của một quan hệ R từ A đến B là mn .
Tên miền và phạm vi
Nếu có hai tập A và B và quan hệ R có cặp thứ tự (x, y), thì -
Các domaincủa R, Dom (R), là tập $ \ lbrace x \: | \: (x, y) \ trong R \: cho \: một số \: y \: trong \: B \ rbrace $
Các range của R, Ran (R), là tập hợp $ \ lbrace y \: | \: (x, y) \ trong R \: for \: some \: x \: in \: A \ rbrace $
Ví dụ
Cho, $ A = \ lbrace 1, 2, 9 \ rbrace $ và $ B = \ lbrace 1, 3, 7 \ rbrace $
Trường hợp 1 - Nếu quan hệ R là 'bằng' thì $ R = \ lbrace (1, 1), (3, 3) \ rbrace $
Dom (R) = $ \ lbrace 1, 3 \ rbrace, Ran (R) = \ lbrace 1, 3 \ rbrace $
Trường hợp 2 - Nếu quan hệ R là 'nhỏ hơn' thì $ R = \ lbrace (1, 3), (1, 7), (2, 3), (2, 7) \ rbrace $
Dom (R) = $ \ lbrace 1, 2 \ rbrace, Ran (R) = \ lbrace 3, 7 \ rbrace $
Trường hợp 3 - Nếu quan hệ R 'lớn hơn' thì $ R = \ lbrace (2, 1), (9, 1), (9, 3), (9, 7) \ rbrace $
Dom (R) = $ \ lbrace 2, 9 \ rbrace, Ran (R) = \ lbrace 1, 3, 7 \ rbrace $
Biểu diễn các mối quan hệ bằng cách sử dụng Đồ thị
Một mối quan hệ có thể được biểu diễn bằng biểu đồ có hướng.
Số đỉnh trong đồ thị bằng số phần tử trong tập hợp mà từ đó quan hệ đã được xác định. Với mỗi cặp có thứ tự (x, y) trong quan hệ R, sẽ có một cạnh có hướng từ đỉnh 'x' đến đỉnh 'y'. Nếu có một cặp có thứ tự (x, x), sẽ có vòng lặp tự trên đỉnh 'x'.
Giả sử, có một quan hệ $ R = \ lbrace (1, 1), (1,2), (3, 2) \ rbrace $ trên tập $ S = \ lbrace 1, 2, 3 \ rbrace $, nó có thể là được biểu diễn bằng biểu đồ sau:
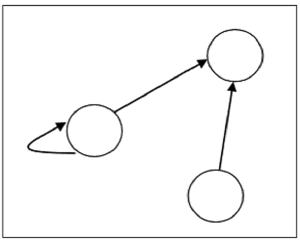
Các loại quan hệ
Các Empty Relation giữa các tập X và Y, hoặc trên E, là tập rỗng $ \ blankset $
Các Full Relation giữa tập X và Y là tập $ X \ times Y $
Các Identity Relationtrên tập X là tập $ \ lbrace (x, x) | x \ trong X \ rbrace $
Quan hệ nghịch đảo R 'của quan hệ R được định nghĩa là - $ R' = \ lbrace (b, a) | (a, b) \ trong R \ rbrace $
Example - Nếu $ R = \ lbrace (1, 2), (2, 3) \ rbrace $ thì $ R '$ sẽ là $ \ lbrace (2, 1), (3, 2) \ rbrace $
Một quan hệ R trên tập A được gọi là Reflexive nếu $ \ forall a \ trong A $ liên quan đến a (aRa giữ)
Example - Quan hệ $ R = \ lbrace (a, a), (b, b) \ rbrace $ trên tập $ X = \ lbrace a, b \ rbrace $ là quan hệ phản xạ.
Một quan hệ R trên tập A được gọi là Irreflexive nếu không có $ a \ trong A $ liên quan đến a (aRa không giữ).
Example - Quan hệ $ R = \ lbrace (a, b), (b, a) \ rbrace $ trên tập $ X = \ lbrace a, b \ rbrace $ là không linh hoạt.
Một quan hệ R trên tập A được gọi là Symmetric nếu $ xRy $ ngụ ý $ yRx $, $ \ forall x \ in A $ và $ \ forall y \ in A $.
Example - Quan hệ $ R = \ lbrace (1, 2), (2, 1), (3, 2), (2, 3) \ rbrace $ trên tập $ A = \ lbrace 1, 2, 3 \ rbrace $ là đối xứng.
Một quan hệ R trên tập A được gọi là Anti-Symmetric nếu $ xRy $ và $ yRx $ ngụ ý $ x = y \: \ forall x \ in A $ và $ \ forall y \ in A $.
Example - Quan hệ $ R = \ lbrace (x, y) \ với N | \: x \ leq y \ rbrace $ là phản đối xứng vì $ x \ leq y $ và $ y \ leq x $ ngụ ý $ x = y $ .
Một quan hệ R trên tập A được gọi là Transitive nếu $ xRy $ và $ yRz $ ngụ ý $ xRz, \ forall x, y, z \ in A $.
Example - Quan hệ $ R = \ lbrace (1, 2), (2, 3), (1, 3) \ rbrace $ trên tập $ A = \ lbrace 1, 2, 3 \ rbrace $ có tính bắc cầu.
Một mối quan hệ là một Equivalence Relation nếu nó là phản xạ, đối xứng và bắc cầu.
Example - Quan hệ $ R = \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \ rbrace $ trên tập $ A = \ lbrace 1, 2, 3 \ rbrace $ là một quan hệ tương đương vì nó là quan hệ phản xạ, đối xứng và bắc cầu.