Toán học rời rạc - Cây kéo dài
Cây bao trùm của đồ thị vô hướng được kết nối $ G $ là cây bao gồm tối thiểu tất cả các đỉnh của $ G $. Một biểu đồ có thể có nhiều cây bao trùm.
Thí dụ
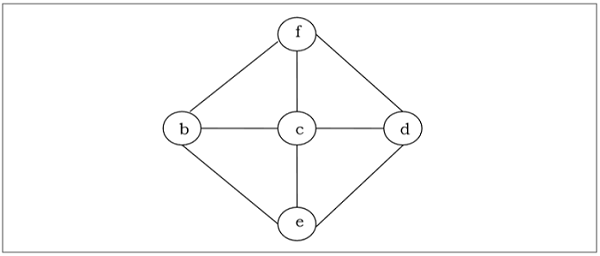
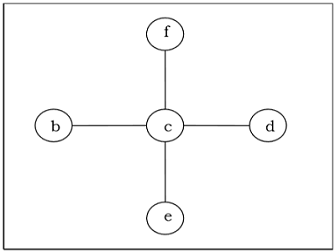
Cây kéo dài tối thiểu
Cây khung có trọng số được ấn định nhỏ hơn hoặc bằng trọng số của mọi cây khung có thể có của đồ thị $ G $ có trọng số, được kết nối và vô hướng, nó được gọi là cây khung tối thiểu (MST). Trọng số của cây khung là tổng của tất cả các trọng số được gán cho mỗi cạnh của cây khung.
Thí dụ
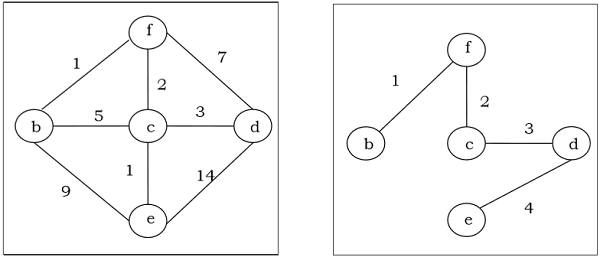
Thuật toán Kruskal
Thuật toán Kruskal là một thuật toán tham lam tìm cây bao trùm tối thiểu cho một đồ thị có trọng số được kết nối. Nó tìm thấy một cây của đồ thị đó bao gồm mọi đỉnh và tổng trọng số của tất cả các cạnh trong cây nhỏ hơn hoặc bằng mọi cây khung có thể có.
Thuật toán
Step 1 - Sắp xếp tất cả các cạnh của đồ thị đã cho $ G (V, E) $ theo thứ tự tăng dần theo trọng số các cạnh của chúng.
Step 2 - Chọn cạnh có trọng số nhỏ nhất từ biểu đồ và kiểm tra xem nó có tạo thành một chu trình với cây khung đã hình thành cho đến nay hay không.
Step 3 - Nếu không có chu trình, hãy đưa cạnh này vào cây khung còn lại thì loại bỏ nó.
Step 4 - Lặp lại Bước 2 và Bước 3 cho đến khi số cạnh $ (V-1) $ còn lại trong cây khung.
Problem
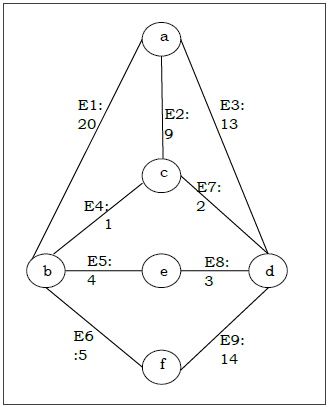
Giả sử chúng ta muốn tìm cây bao trùm nhỏ nhất cho đồ thị G sau đây bằng thuật toán Kruskal.
Solution
Từ đồ thị trên, chúng ta xây dựng bảng sau:
| Số cạnh. | Cặp đỉnh | Trọng lượng cạnh |
|---|---|---|
| E1 | (a, b) | 20 |
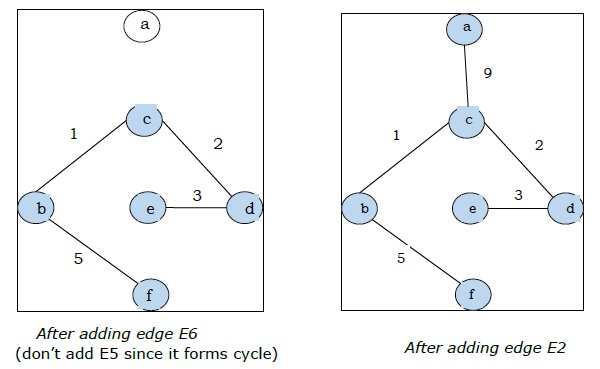
| E2 | (AC) | 9 |
| E3 | (a, d) | 13 |
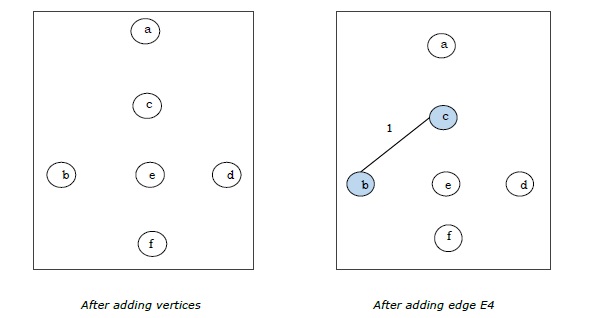
| E 4 | (b, c) | 1 |
| E5 | (là) | 4 |
| E6 | (b, f) | 5 |
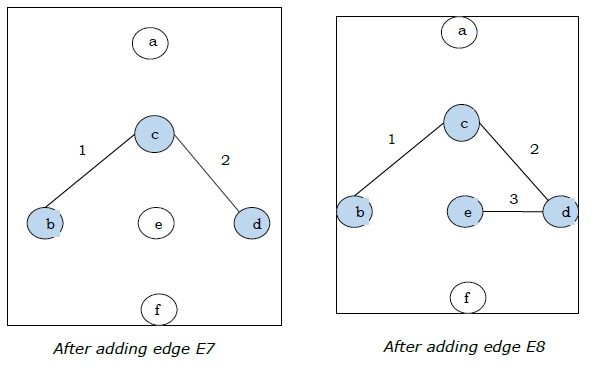
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
Bây giờ chúng ta sẽ sắp xếp lại bảng theo thứ tự tăng dần đối với trọng lượng của Edge -
| Số cạnh. | Cặp đỉnh | Trọng lượng cạnh |
|---|---|---|
| E 4 | (b, c) | 1 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (là) | 4 |
| E6 | (b, f) | 5 |
| E2 | (AC) | 9 |
| E3 | (a, d) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
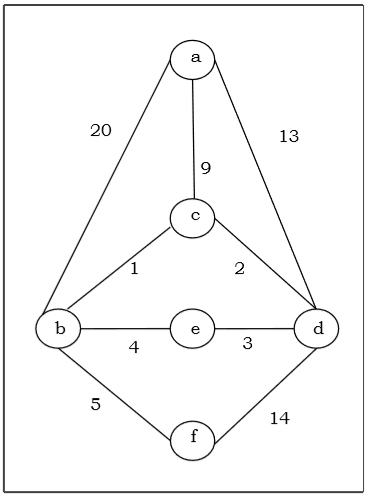
Vì chúng ta có tất cả 5 cạnh trong hình cuối cùng, chúng ta dừng thuật toán và đây là cây bao trùm nhỏ nhất và tổng trọng số của nó là $ (1 + 2 + 3 + 5 + 9) = 20 $.
Thuật toán Prim
Thuật toán Prim, được phát hiện vào năm 1930 bởi các nhà toán học, Vojtech Jarnik và Robert C. Prim, là một thuật toán tham lam tìm một cây bao trùm tối thiểu cho một đồ thị có trọng số được kết nối. Nó tìm thấy một cây của đồ thị đó bao gồm mọi đỉnh và tổng trọng số của tất cả các cạnh trong cây nhỏ hơn hoặc bằng mọi cây khung có thể có. Thuật toán của Prim nhanh hơn trên đồ thị dày đặc.
Thuật toán
Khởi tạo cây khung tối thiểu với một đỉnh duy nhất, được chọn ngẫu nhiên từ biểu đồ.
Lặp lại bước 3 và 4 cho đến khi tất cả các đỉnh được bao gồm trong cây.
Chọn một cạnh nối cây với một đỉnh chưa có trong cây, sao cho trọng lượng của cạnh là nhỏ nhất và việc bao gồm cạnh không tạo thành một chu trình.
Thêm cạnh đã chọn và đỉnh mà nó kết nối với cây.
Problem
Giả sử chúng ta muốn tìm cây bao trùm tối thiểu cho đồ thị G sau đây bằng thuật toán Prim.
Solution
Ở đây chúng ta bắt đầu với đỉnh 'a' và tiếp tục.
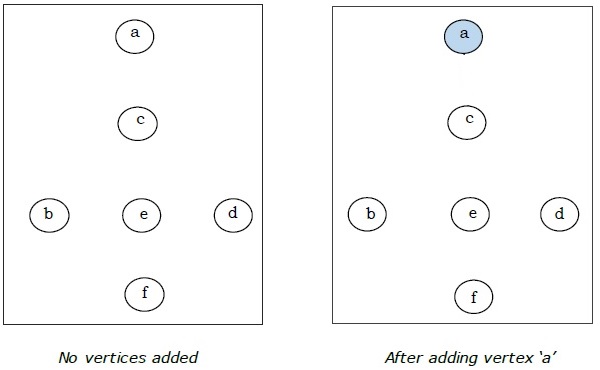
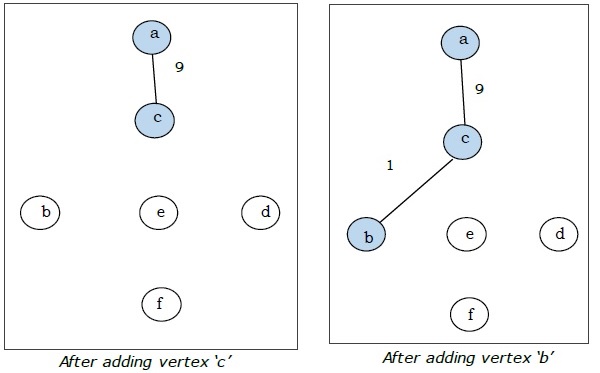
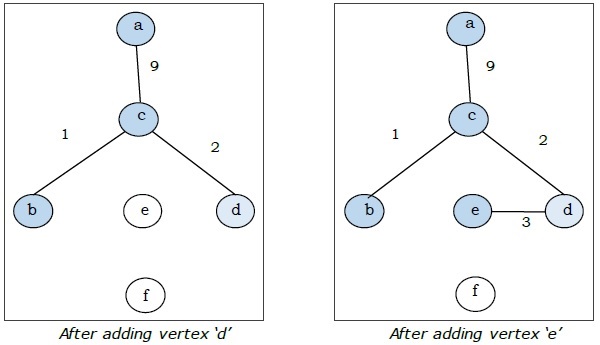
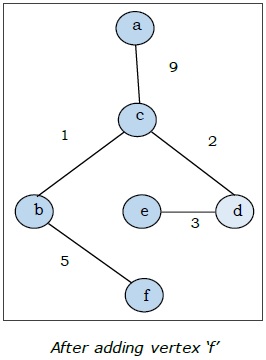
Đây là cây khung nhỏ nhất và tổng trọng lượng của nó là $ (1 + 2 + 3 + 5 + 9) = 20 $.