Giới thiệu về cây cối

Treelà một cấu trúc rời rạc đại diện cho các mối quan hệ thứ bậc giữa các phần tử hoặc các nút riêng lẻ. Cây trong đó cây bố mẹ có không quá hai cây con được gọi là cây nhị phân.

Cây và các thuộc tính của nó

Definition- Cây là một đồ thị vô hướng xoay chiều liên thông. Có một đường đi duy nhất giữa mọi cặp đỉnh trong $ G $. Một cây có N số đỉnh chứa $ (N-1) $ số cạnh. Đỉnh có 0 độ được gọi là gốc của cây. Đỉnh có độ cao 1 được gọi là nút lá của cây và đỉnh của nút bên trong ít nhất là 2.

Example - Sau đây là ví dụ về cây -

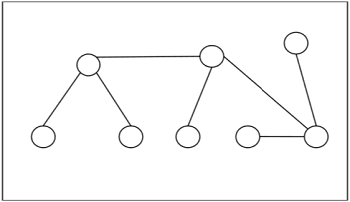
Các trung tâm và hai trung tâm của một cây

Tâm của cây là đỉnh có độ lệch tâm tối thiểu. Độ lệch tâm của đỉnh $ X $ trong cây $ G $ là khoảng cách lớn nhất giữa đỉnh $ X $ và bất kỳ đỉnh nào khác của cây. Độ lệch tâm lớn nhất là đường kính cây. Nếu một cây chỉ có một trung tâm, nó được gọi là Cây trung tâm và nếu một cây chỉ có nhiều hơn một trung tâm, nó được gọi là Cây trung tâm. Mọi cây đều là trung tâm hoặc hai trung tâm.

Thuật toán tìm tâm và tâm kép của cây

Step 1 - Loại bỏ tất cả các đỉnh bậc 1 khỏi cây đã cho và cũng loại bỏ các cạnh tới của chúng.

Step 2- Lặp lại bước 1 cho đến khi còn lại một đỉnh duy nhất hoặc hai đỉnh nối bởi một cạnh. Nếu bên trái một đỉnh thì nó là tâm của cây và nếu hai đỉnh được ghép bởi một cạnh còn lại thì nó là tâm của cây.

Problem 1

Tìm ra tâm / tâm bi của cây sau:

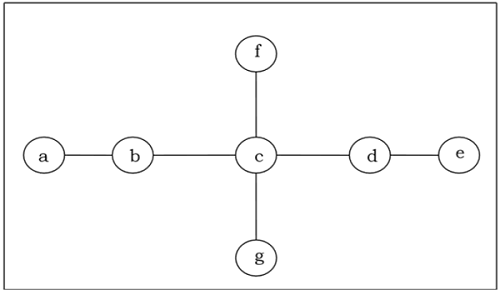
Solution

Đầu tiên, chúng ta sẽ loại bỏ tất cả các đỉnh của bậc 1 và cũng loại bỏ các cạnh tới của chúng và nhận được cây sau:

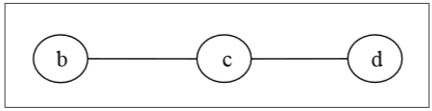
Một lần nữa, chúng ta sẽ loại bỏ tất cả các đỉnh của bậc 1 và cũng loại bỏ các cạnh tới của chúng và nhận được cây sau:

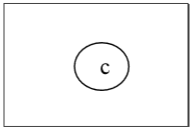
Cuối cùng, chúng ta có một đỉnh duy nhất 'c' và chúng ta dừng thuật toán. Vì có một đỉnh duy nhất nên cây này có một tâm là 'c' và cây này là cây trung tâm.

Problem 2

Tìm ra tâm / tâm bi của cây sau:

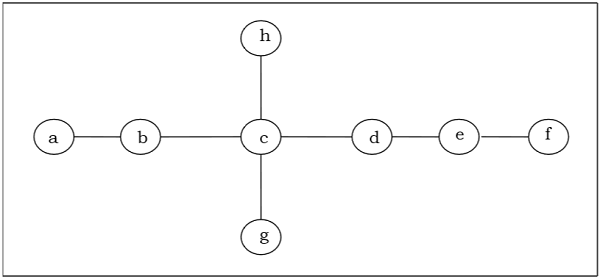
Solution

Đầu tiên, chúng ta sẽ loại bỏ tất cả các đỉnh của bậc 1 và cũng loại bỏ các cạnh tới của chúng và nhận được cây sau:

Một lần nữa, chúng ta sẽ loại bỏ tất cả các đỉnh của bậc 1 và cũng loại bỏ các cạnh tới của chúng và nhận được cây sau:

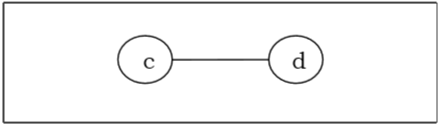
Cuối cùng, chúng tôi còn lại hai đỉnh 'c' và 'd', do đó chúng tôi dừng thuật toán. Khi hai đỉnh được nối bởi một cạnh còn lại, cây này có hai tâm 'cd' và cây là hai tâm.

Cây được gắn nhãn

Definition- Cây có nhãn là cây mà các đỉnh của chúng được gán các số duy nhất từ 1 đến n. Chúng ta có thể đếm những cây như vậy cho các giá trị nhỏ của n bằng tay để phỏng đoán một công thức tổng quát. Số cây có nhãn gồm n số đỉnh là $ n ^ {n-2} $. Hai cây có nhãn là đẳng cấu nếu đồ thị của chúng là đẳng cấu và các điểm tương ứng của hai cây có nhãn giống nhau.

Thí dụ

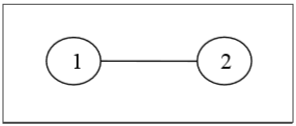
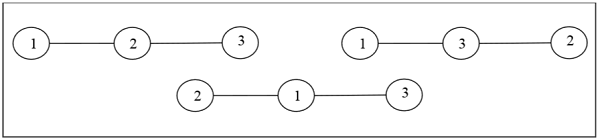
Cây không dán nhãn

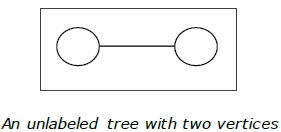
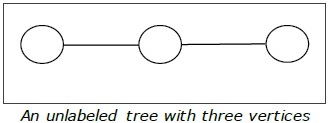
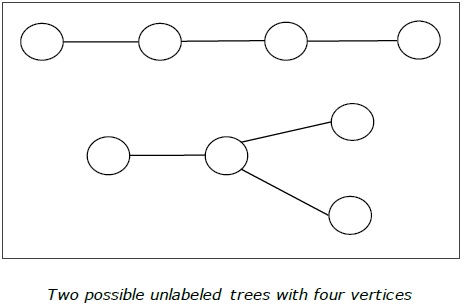
Definition- Cây không có nhãn là cây mà các đỉnh không được gán bất kỳ số nào. Số cây có nhãn gồm n số đỉnh là $ \ frac {(2n)!} {(N + 1)! N! } $ ( số Catalan ^thứ n )

Thí dụ

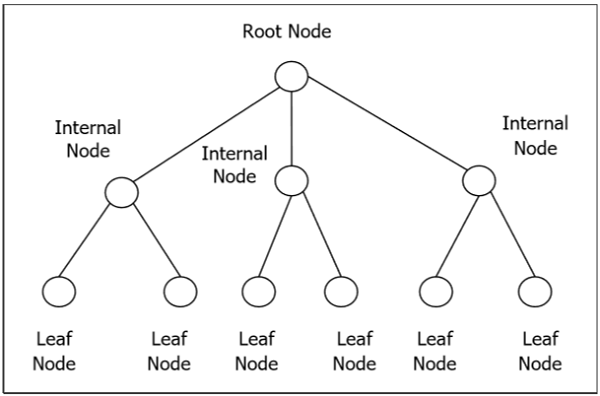
Cây có rễ

Cây có gốc $ G $ là một đồ thị mạch hở liên thông với một nút đặc biệt được gọi là gốc của cây và mọi cạnh đều bắt nguồn trực tiếp hoặc gián tiếp từ gốc. Cây có rễ có thứ tự là cây có rễ có thứ tự con của mỗi đỉnh bên trong. Nếu mỗi đỉnh bên trong của một cây gốc có không quá m con, nó được gọi là m-ary tree. Nếu mỗi đỉnh bên trong của một cây gốc có đúng m con thì nó được gọi là một cây đầy đủ m-ary. Nếu $ m = 2 $, cây gốc được gọi là cây nhị phân.

Cây tìm kiếm nhị phân

Cây tìm kiếm nhị phân là cây nhị phân thỏa mãn thuộc tính sau:

$ X $ trong cây con bên trái của đỉnh $ V, Giá trị (X) \ le Giá trị (V) $
$ Y $ trong cây con bên phải của đỉnh $ V, Giá trị (Y) \ ge Giá trị (V) $

Vì vậy, giá trị của tất cả các đỉnh của cây con bên trái của nút trong $ V $ nhỏ hơn hoặc bằng $ V $ và giá trị của tất cả các đỉnh của cây con bên phải của nút trong $ V $ lớn hơn hoặc bằng $ V $. Số lượng liên kết từ nút gốc đến nút sâu nhất là chiều cao của Cây tìm kiếm nhị phân.

Thí dụ

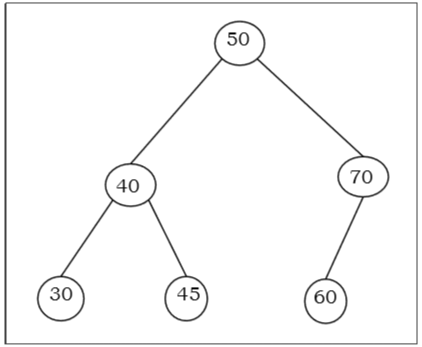
Thuật toán tìm kiếm khóa trong BST

BST_Search(x, k) 
if ( x = NIL or k = Value[x] ) 
   return x; 
if ( k < Value[x]) 
   return BST_Search (left[x], k); 
else  
   return BST_Search (right[x], k)

Độ phức tạp của cây tìm kiếm nhị phân

	Trường hợp trung bình	Trường hợp xấu nhất
Không gian phức tạp	Trên)	Trên)
Tìm kiếm phức tạp	O (log n)	Trên)
Độ phức tạp chèn	O (log n)	Trên)
Xóa độ phức tạp	O (log n)	Trên)