Đơn giản hóa các hàm Boolean
Đơn giản hóa bằng cách sử dụng các hàm đại số
Trong cách tiếp cận này, một biểu thức Boolean được tối thiểu hóa thành một biểu thức tương đương bằng cách áp dụng các nhận dạng Boolean.
Vấn đề 1
Giảm thiểu biểu thức Boolean sau bằng cách sử dụng danh tính Boolean:
$$ F (A, B, C) = A'B + BC '+ BC + AB'C' $$
Giải pháp
Cho trước, $ F (A, B, C) = A'B + BC '+ BC + AB'C' $
Hoặc, $ F (A, B, C) = A'B + (BC '+ BC') + BC + AB'C '$
[Theo luật bất biến, BC '= BC' + BC ']
Hoặc, $ F (A, B, C) = A'B + (BC '+ BC) + (BC' + AB'C ') $
Hoặc, $ F (A, B, C) = A'B + B (C '+ C) + C' (B + AB ') $
[Theo luật phân phối]
Hoặc, $ F (A, B, C) = A'B + B.1 + C '(B + A) $
[(C '+ C) = 1 và định luật hấp thụ (B + AB') = (B + A)]
Hoặc, $ F (A, B, C) = A'B + B + C '(B + A) $
[B.1 = B]
Hoặc, $ F (A, B, C) = B (A '+ 1) + C' (B + A) $
Hoặc, $ F (A, B, C) = B.1 + C '(B + A) $
[(A '+ 1) = 1]
Hoặc, $ F (A, B, C) = B + C '(B + A) $
[Như, B.1 = B]
Hoặc, $ F (A, B, C) = B + BC '+ AC' $
Hoặc, $ F (A, B, C) = B (1 + C ') + AC' $
Hoặc, $ F (A, B, C) = B.1 + AC '$
[Như, (1 + C ') = 1]
Hoặc, $ F (A, B, C) = B + AC '$
[Như, B.1 = B]
Vì vậy, $ F (A, B, C) = B + AC '$ là dạng cực tiểu.
Vấn đề 2
Giảm thiểu biểu thức Boolean sau bằng cách sử dụng danh tính Boolean:
$$ F (A, B, C) = (A + B) (A + C) $$
Giải pháp
Cho trước, $ F (A, B, C) = (A + B) (A + C) $
Hoặc, $ F (A, B, C) = AA + AC + BA + BC $ [Áp dụng quy tắc phân phối]
Hoặc, $ F (A, B, C) = A + AC + BA + BC $ [Áp dụng định luật Idempotent]
Hoặc, $ F (A, B, C) = A (1 + C) + BA + BC $ [Áp dụng Luật phân phối]
Hoặc, $ F (A, B, C) = A + BA + BC $ [Áp dụng Luật thống trị]
Hoặc, $ F (A, B, C) = (A + 1) .A + BC $ [Áp dụng Luật phân phối]
Hoặc, $ F (A, B, C) = 1.A + BC $ [Áp dụng Luật thống trị]
Hoặc, $ F (A, B, C) = A + BC $ [Áp dụng Luật thống trị]
Vậy $ F (A, B, C) = A + BC $ là dạng cực tiểu.
Bản đồ Karnaugh
Bản đồ Karnaugh (K – map), được Maurice Karnaughin giới thiệu vào năm 1953, là một biểu diễn dạng lưới của bảng chân trị được sử dụng để đơn giản hóa các biểu thức đại số boolean. Một bản đồ Karnaugh có số không và một mục ở các vị trí khác nhau. Nó cung cấp nhóm các biểu thức Boolean với nhau với các yếu tố chung và loại bỏ các biến không mong muốn khỏi biểu thức. Trong bản đồ K, việc vượt qua ranh giới ô dọc hoặc ngang luôn là sự thay đổi chỉ một biến.
ví dụ 1
Một bảng chân lý tùy ý được lấy bên dưới:
| A | B | A hoạt động B |
|---|---|---|
| 0 | 0 | w |
| 0 | 1 | x |
| 1 | 0 | y |
| 1 | 1 | z |
Bây giờ chúng ta sẽ tạo một bản đồ k cho bảng sự thật ở trên -

Ví dụ 2
Bây giờ chúng ta sẽ tạo một ánh xạ K cho biểu thức - AB + A'B '
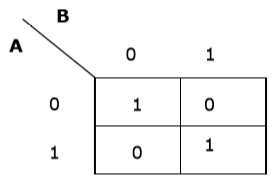
Đơn giản hóa bằng K-map
K-map sử dụng một số quy tắc để đơn giản hóa các biểu thức Boolean bằng cách kết hợp các ô liền kề với nhau thành một số hạng. Các quy tắc được mô tả bên dưới -
Rule 1 - Bất kỳ ô nào chứa số 0 đều không thể được nhóm lại.
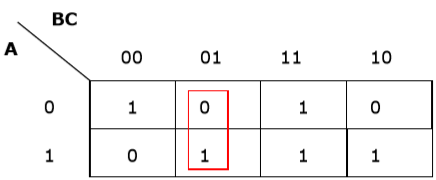
Nhóm sai
Rule 2 - Nhóm phải chứa 2n ô (n bắt đầu từ 1).
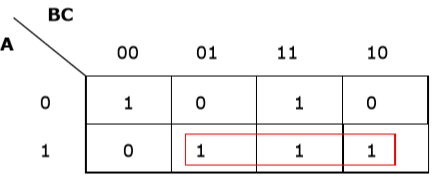
Nhóm sai
Rule 3 - Phân nhóm phải theo chiều ngang hoặc chiều dọc, nhưng không được theo đường chéo.
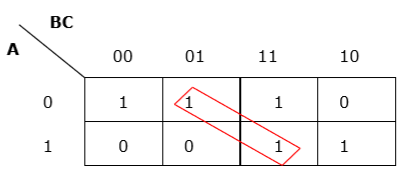
Nhóm đường chéo sai
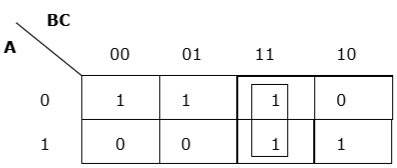
Phân nhóm ngành dọc thích hợp
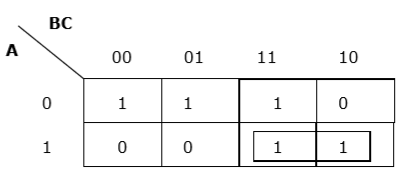
Phân nhóm theo chiều ngang thích hợp
Rule 4 - Các nhóm phải được bảo hiểm càng nhiều càng tốt.
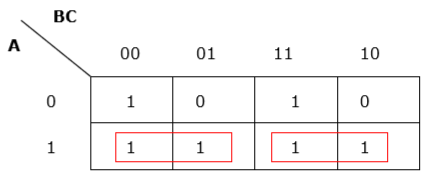
Nhóm không đủ
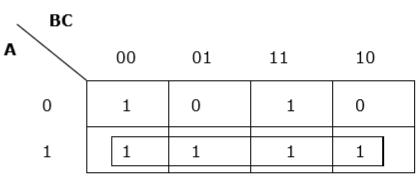
Phân nhóm thích hợp
Rule 5 - Nếu 1 trong bất kỳ ô nào không thể được nhóm với bất kỳ ô nào khác, nó sẽ hoạt động như một nhóm chính nó.
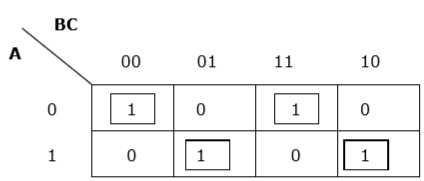
Phân nhóm thích hợp
Rule 6 - Các nhóm có thể trùng nhau nhưng nên có càng ít nhóm càng tốt.
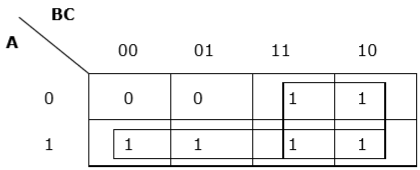
Phân nhóm thích hợp
Rule 7 - Ô / ô ngoài cùng bên trái có thể được nhóm với ô / ô ngoài cùng bên phải và ô / ô trên cùng có thể được nhóm với ô / ô ngoài cùng.
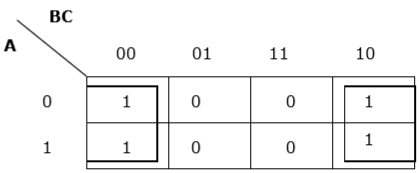
Phân nhóm thích hợp
Vấn đề
Giảm thiểu biểu thức Boolean sau đây bằng K-map -
$$ F (A, B, C) = A'BC + A'BC '+ AB'C' + AB'C $$
Giải pháp
Mỗi thuật ngữ được đưa vào k-map và chúng tôi nhận được những điều sau:
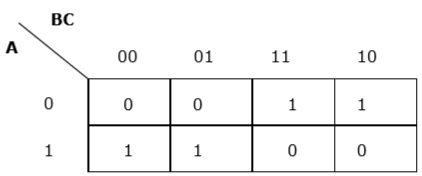
Bản đồ K cho F (A, B, C)
Bây giờ chúng ta sẽ nhóm các ô của 1 theo các quy tắc đã nêu ở trên -
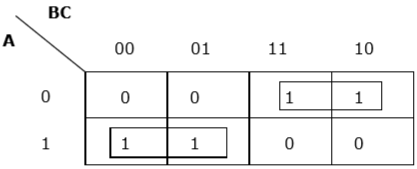
Bản đồ K cho F (A, B, C)
Chúng tôi có hai nhóm được gọi là $ A'B $ và $ AB '$. Do đó, $ F (A, B, C) = A'B + AB '= A \ oplus B $. Nó là hình thức thu nhỏ.