Học máy với Python - Hướng dẫn nhanh
Chúng ta đang sống trong 'thời đại dữ liệu' được làm giàu với sức mạnh tính toán tốt hơn và nhiều tài nguyên lưu trữ hơn,. Dữ liệu hoặc thông tin này đang tăng lên từng ngày, nhưng thách thức thực sự là hiểu được tất cả dữ liệu. Các doanh nghiệp và tổ chức đang cố gắng giải quyết vấn đề này bằng cách xây dựng các hệ thống thông minh sử dụng các khái niệm và phương pháp luận từ Khoa học dữ liệu, Khai thác dữ liệu và Máy học. Trong số đó, học máy là lĩnh vực khoa học máy tính thú vị nhất. Sẽ không sai nếu chúng ta gọi học máy là ứng dụng và khoa học của các thuật toán mang lại cảm giác cho dữ liệu.
Học máy là gì?
Học máy (ML) là lĩnh vực khoa học máy tính với sự trợ giúp của hệ thống máy tính có thể cung cấp cảm giác cho dữ liệu theo cách giống như cách con người làm.
Nói cách đơn giản, ML là một loại trí tuệ nhân tạo trích xuất các mẫu ra khỏi dữ liệu thô bằng cách sử dụng một thuật toán hoặc phương pháp. Trọng tâm chính của ML là cho phép các hệ thống máy tính học hỏi kinh nghiệm mà không cần được lập trình rõ ràng hoặc có sự can thiệp của con người.
Cần cho Học máy
Con người, tại thời điểm này, là loài thông minh và tiên tiến nhất trên trái đất vì họ có thể suy nghĩ, đánh giá và giải quyết các vấn đề phức tạp. Mặt khác, AI vẫn đang trong giai đoạn sơ khai và chưa vượt qua trí thông minh của con người về nhiều mặt. Sau đó, câu hỏi đặt ra là cần làm cho máy học là gì? Lý do phù hợp nhất để làm điều này là “đưa ra quyết định, dựa trên dữ liệu, với hiệu quả và quy mô”.
Gần đây, các tổ chức đang đầu tư mạnh mẽ vào các công nghệ mới hơn như Trí tuệ nhân tạo, Học máy và Học sâu để lấy thông tin quan trọng từ dữ liệu nhằm thực hiện một số nhiệm vụ trong thế giới thực và giải quyết vấn đề. Chúng ta có thể gọi đó là các quyết định dựa trên dữ liệu do máy móc thực hiện, đặc biệt là để tự động hóa quy trình. Những quyết định theo hướng dữ liệu này có thể được sử dụng, thay vì sử dụng logic lập trình, trong các vấn đề vốn dĩ không thể lập trình được. Thực tế là chúng ta không thể làm được nếu không có trí thông minh của con người, nhưng khía cạnh khác là tất cả chúng ta cần giải quyết các vấn đề trong thế giới thực với hiệu quả ở quy mô lớn. Đó là lý do tại sao nhu cầu về học máy phát sinh.
Tại sao & Khi nào nên Học Máy móc?
Chúng ta đã thảo luận về sự cần thiết của việc học máy, nhưng một câu hỏi khác đặt ra là chúng ta phải làm cho máy học trong những tình huống nào? Có thể có một số trường hợp mà chúng ta cần máy móc để đưa ra các quyết định dựa trên dữ liệu với hiệu quả và ở quy mô lớn. Sau đây là một số trường hợp như vậy mà việc chế tạo máy học sẽ hiệu quả hơn -
Thiếu chuyên môn của con người
Kịch bản đầu tiên trong đó chúng ta muốn một cỗ máy học hỏi và đưa ra các quyết định theo hướng dữ liệu, có thể là lĩnh vực thiếu chuyên môn của con người. Các ví dụ có thể là điều hướng trong các lãnh thổ hoặc hành tinh không gian không xác định.
Các tình huống động
Có một số kịch bản có bản chất động tức là chúng liên tục thay đổi theo thời gian. Trong trường hợp của những tình huống và hành vi này, chúng tôi muốn một cỗ máy học hỏi và đưa ra các quyết định theo hướng dữ liệu. Một số ví dụ có thể là kết nối mạng và tính sẵn có của cơ sở hạ tầng trong một tổ chức.
Khó khăn trong việc chuyển đổi kiến thức chuyên môn thành các nhiệm vụ tính toán
Có thể có nhiều lĩnh vực khác nhau mà con người có chuyên môn của họ ,; tuy nhiên, họ không thể chuyển kiến thức chuyên môn này thành các nhiệm vụ tính toán. Trong những trường hợp như vậy, chúng tôi muốn học máy. Các ví dụ có thể là các lĩnh vực nhận dạng giọng nói, các nhiệm vụ nhận thức, v.v.
Mô hình học máy
Trước khi thảo luận về mô hình học máy, chúng ta phải hiểu định nghĩa chính thức sau đây của ML do giáo sư Mitchell đưa ra:
“Một chương trình máy tính được cho là học hỏi từ trải nghiệm E đối với một số loại nhiệm vụ T và thước đo hiệu suất P, nếu hiệu suất của nó ở các nhiệm vụ trong T, được đo bằng P, cải thiện theo kinh nghiệm E.”
Định nghĩa trên về cơ bản tập trung vào ba tham số, cũng là thành phần chính của bất kỳ thuật toán học tập nào, đó là Nhiệm vụ (T), Hiệu suất (P) và kinh nghiệm (E). Trong ngữ cảnh này, chúng ta có thể đơn giản hóa định nghĩa này là:
ML là một lĩnh vực AI bao gồm các thuật toán học tập -
Cải thiện hiệu suất của họ (P)
Khi thực hiện một số nhiệm vụ (T)
Theo thời gian với kinh nghiệm (E)
Dựa trên những điều trên, sơ đồ sau đại diện cho Mô hình Học máy -

Hãy để chúng tôi thảo luận chi tiết hơn về chúng ngay bây giờ -
Nhiệm vụ (T)
Từ góc độ vấn đề, chúng ta có thể định nghĩa nhiệm vụ T là vấn đề trong thế giới thực cần giải quyết. Vấn đề có thể là bất cứ điều gì như tìm giá nhà tốt nhất ở một vị trí cụ thể hoặc tìm chiến lược tiếp thị tốt nhất, v.v. Mặt khác, nếu chúng ta nói về máy học, định nghĩa của nhiệm vụ là khác bởi vì rất khó để giải quyết các nhiệm vụ dựa trên ML bằng cách cách tiếp cận lập trình thông thường.
Nhiệm vụ T được cho là một nhiệm vụ dựa trên ML khi nó dựa trên quy trình và hệ thống phải tuân theo để hoạt động trên các điểm dữ liệu. Ví dụ về các nhiệm vụ dựa trên ML là Phân loại, Hồi quy, Chú thích có cấu trúc, Phân cụm, Phiên mã, v.v.
Kinh nghiệm (E)
Như tên cho thấy, nó là kiến thức thu được từ các điểm dữ liệu được cung cấp cho thuật toán hoặc mô hình. Sau khi được cung cấp tập dữ liệu, mô hình sẽ chạy lặp đi lặp lại và sẽ học một số mẫu vốn có. Do đó, sự học hỏi có được gọi là kinh nghiệm (E). Tương tự với việc học tập của con người, chúng ta có thể nghĩ về tình huống này như trong đó một con người đang học hỏi hoặc đạt được một số kinh nghiệm từ các thuộc tính khác nhau như tình huống, mối quan hệ, v.v. Học tập có giám sát, không giám sát và tăng cường là một số cách để học hỏi hoặc tích lũy kinh nghiệm. Kinh nghiệm thu được từ mô hình ML hoặc thuật toán sẽ được sử dụng để giải quyết nhiệm vụ T.
Hiệu suất (P)
Một thuật toán ML được cho là thực hiện nhiệm vụ và tích lũy kinh nghiệm theo thời gian. Thước đo cho biết thuật toán ML có hoạt động như mong đợi hay không là hiệu suất của nó (P). P về cơ bản là một số liệu định lượng cho biết cách một mô hình đang thực hiện nhiệm vụ, T, sử dụng kinh nghiệm của nó, E. Có nhiều số liệu giúp hiểu hiệu suất ML, chẳng hạn như điểm chính xác, điểm F1, ma trận nhầm lẫn, độ chính xác, thu hồi , độ nhạy, v.v.
Những thách thức trong học máy
Trong khi Học máy đang phát triển nhanh chóng, tạo ra những bước tiến đáng kể với an ninh mạng và ô tô tự hành, thì toàn bộ mảng AI này vẫn còn một chặng đường dài phía trước. Lý do đằng sau là ML đã không thể vượt qua một số thử thách. Những thách thức mà ML đang phải đối mặt hiện tại là -
Quality of data- Có dữ liệu chất lượng tốt cho các thuật toán ML là một trong những thách thức lớn nhất. Việc sử dụng dữ liệu chất lượng thấp dẫn đến các vấn đề liên quan đến tiền xử lý dữ liệu và trích xuất tính năng.
Time-Consuming task - Một thách thức khác mà các mô hình ML phải đối mặt là tiêu tốn thời gian đặc biệt cho việc thu thập dữ liệu, trích xuất và truy xuất tính năng.
Lack of specialist persons - Vì công nghệ ML vẫn còn trong giai đoạn sơ khai, nên việc có sẵn nguồn lực chuyên gia là một công việc khó khăn.
No clear objective for formulating business problems - Không có mục tiêu rõ ràng và mục tiêu được xác định rõ ràng cho các vấn đề kinh doanh là một thách thức quan trọng khác đối với ML vì công nghệ này vẫn chưa trưởng thành.
Issue of overfitting & underfitting - Nếu mô hình được trang bị quá mức hoặc thiếu trang bị, nó không thể được đại diện tốt cho sự cố.
Curse of dimensionality- Một thách thức khác mà mô hình ML gặp phải là quá nhiều tính năng của các điểm dữ liệu. Đây có thể là một trở ngại thực sự.
Difficulty in deployment - Sự phức tạp của mô hình ML khiến nó khá khó triển khai trong cuộc sống thực.
Các ứng dụng của Học máy
Học máy là công nghệ phát triển nhanh chóng nhất và theo các nhà nghiên cứu, chúng ta đang ở trong năm vàng của AI và ML. Nó được sử dụng để giải quyết nhiều vấn đề phức tạp trong thế giới thực mà không thể giải quyết bằng phương pháp truyền thống. Sau đây là một số ứng dụng trong thế giới thực của ML -
Phân tích cảm xúc
Phân tích tình cảm
Phát hiện và ngăn ngừa lỗi
Dự báo thời tiết và dự đoán
Phân tích và dự báo thị trường chứng khoán
Tổng hợp giọng nói
Nhận dạng giọng nói
Phân khúc khách hàng
Nhận dạng đối tượng
Phát hiện gian lận
Phòng chống gian lận
Giới thiệu sản phẩm cho khách hàng khi mua sắm trực tuyến.
Giới thiệu về Python
Python là một ngôn ngữ lập trình hướng đối tượng phổ biến có các tính năng của ngôn ngữ lập trình cấp cao. Cú pháp dễ học và khả năng di động của nó khiến nó trở nên phổ biến ngày nay. Các dữ kiện sau đây cung cấp cho chúng ta sự giới thiệu về Python:
Python được phát triển bởi Guido van Rossum tại Stichting Mathematisch Centrum ở Hà Lan.
Nó được viết như là sự kế thừa của ngôn ngữ lập trình có tên là 'ABC'.
Phiên bản đầu tiên được phát hành vào năm 1991.
Cái tên Python do Guido van Rossum chọn từ một chương trình truyền hình có tên Monty Python's Flying Circus.
Nó là một ngôn ngữ lập trình mã nguồn mở, có nghĩa là chúng ta có thể tự do tải xuống và sử dụng nó để phát triển các chương trình. Nó có thể được tải xuống từ www.python.org .
Ngôn ngữ lập trình Python có các tính năng của cả Java và C. Nó có mã 'C' thanh lịch và mặt khác, nó có các lớp và đối tượng như Java để lập trình hướng đối tượng.
Nó là một ngôn ngữ thông dịch, có nghĩa là mã nguồn của chương trình Python trước tiên sẽ được chuyển đổi thành bytecode và sau đó được thực thi bởi máy ảo Python.
Điểm mạnh và điểm yếu của Python
Mọi ngôn ngữ lập trình đều có một số điểm mạnh cũng như điểm yếu, Python cũng vậy.
Điểm mạnh
Theo các nghiên cứu và khảo sát, Python là ngôn ngữ quan trọng thứ năm cũng như là ngôn ngữ phổ biến nhất cho học máy và khoa học dữ liệu. Chính vì những điểm mạnh sau đây mà Python có:
Easy to learn and understand- Cú pháp của Python đơn giản hơn; do đó nó tương đối dễ dàng, ngay cả đối với người mới bắt đầu, học và hiểu ngôn ngữ.
Multi-purpose language - Python là một ngôn ngữ lập trình đa mục đích vì nó hỗ trợ lập trình cấu trúc, lập trình hướng đối tượng cũng như lập trình chức năng.
Huge number of modules- Python có số lượng lớn các mô-đun để bao gồm mọi khía cạnh của lập trình. Các mô-đun này dễ dàng có sẵn để sử dụng do đó làm cho Python trở thành một ngôn ngữ có thể mở rộng.
Support of open source community- Là ngôn ngữ lập trình mã nguồn mở, Python được hỗ trợ bởi một cộng đồng nhà phát triển rất lớn. Do đó, cộng đồng Python dễ dàng sửa lỗi. Đặc điểm này làm cho Python rất mạnh mẽ và thích nghi.
Scalability - Python là một ngôn ngữ lập trình có thể mở rộng vì nó cung cấp một cấu trúc cải tiến để hỗ trợ các chương trình lớn hơn so với các kịch bản lệnh shell.
Yếu đuối
Mặc dù Python là một ngôn ngữ lập trình phổ biến và mạnh mẽ, nhưng nó có điểm yếu riêng là tốc độ thực thi chậm.
Tốc độ thực thi của Python chậm hơn so với các ngôn ngữ biên dịch vì Python là ngôn ngữ thông dịch. Đây có thể là lĩnh vực cải tiến chính của cộng đồng Python.
Cài đặt Python
Để làm việc bằng Python, trước tiên chúng ta phải cài đặt nó. Bạn có thể thực hiện cài đặt Python theo bất kỳ cách nào trong hai cách sau:
Cài đặt Python riêng lẻ
Sử dụng phân phối Python được đóng gói sẵn - Anaconda
Hãy để chúng tôi thảo luận chi tiết từng vấn đề này.
Cài đặt Python riêng lẻ
Nếu bạn muốn cài đặt Python trên máy tính của mình, thì bạn chỉ cần tải xuống mã nhị phân áp dụng cho nền tảng của mình. Bản phân phối Python có sẵn cho các nền tảng Windows, Linux và Mac.
Sau đây là tổng quan nhanh về cài đặt Python trên các nền tảng nêu trên -
On Unix and Linux platform
Với sự trợ giúp của các bước sau, chúng ta có thể cài đặt Python trên nền tảng Unix và Linux -
Đầu tiên, hãy truy cập https://www.python.org/downloads/.
Tiếp theo, nhấp vào liên kết để tải xuống mã nguồn nén có sẵn cho Unix / Linux.
Bây giờ, Tải xuống và giải nén tệp.
Tiếp theo, chúng ta có thể chỉnh sửa tệp Mô-đun / Thiết lập nếu muốn tùy chỉnh một số tùy chọn.
Tiếp theo, viết lệnh run ./configure script
make
thực hiện cài đặt
On Windows platform
Với sự trợ giúp của các bước sau, chúng tôi có thể cài đặt Python trên nền tảng Windows -
Đầu tiên, hãy truy cập https://www.python.org/downloads/.
Tiếp theo, nhấp vào liên kết cho tệp python-XYZ.msi của trình cài đặt Windows. Ở đây XYZ là phiên bản chúng tôi muốn cài đặt.
Bây giờ, chúng ta phải chạy tệp được tải xuống. Nó sẽ đưa chúng ta đến trình hướng dẫn cài đặt Python, rất dễ sử dụng. Bây giờ, hãy chấp nhận cài đặt mặc định và đợi cho đến khi quá trình cài đặt hoàn tất.
On Macintosh platform
Đối với Mac OS X, Homebrew, một trình cài đặt gói tuyệt vời và dễ sử dụng được khuyên dùng để cài đặt Python 3. Trong trường hợp không có Homebrew, bạn có thể cài đặt nó với sự trợ giúp của lệnh sau:
$ ruby -e "$(curl -fsSL
https://raw.githubusercontent.com/Homebrew/install/master/install)"Nó có thể được cập nhật bằng lệnh dưới đây:
$ brew updateBây giờ, để cài đặt Python3 trên hệ thống của bạn, chúng ta cần chạy lệnh sau:
$ brew install python3Sử dụng phân phối Python được đóng gói sẵn: Anaconda
Anaconda là một biên dịch Python đóng gói có tất cả các thư viện được sử dụng rộng rãi trong Khoa học dữ liệu. Chúng ta có thể làm theo các bước sau để thiết lập môi trường Python bằng Anaconda:
Step1- Đầu tiên, chúng ta cần tải gói cài đặt yêu cầu từ Anaconda Distribution. Liên kết cho cùng làhttps://www.anaconda.com/distribution/. Bạn có thể chọn từ HĐH Windows, Mac và Linux theo yêu cầu của mình.
Step2- Tiếp theo, chọn phiên bản Python mà bạn muốn cài đặt trên máy. Phiên bản Python mới nhất là 3.7. Ở đó, bạn sẽ nhận được các tùy chọn cho cả trình cài đặt Đồ họa 64-bit và 32-bit.
Step3- Sau khi chọn hệ điều hành và phiên bản Python, nó sẽ tải xuống trình cài đặt Anaconda trên máy tính của bạn. Bây giờ, nhấp đúp vào tệp và trình cài đặt sẽ cài đặt gói Anaconda.
Step4 - Để kiểm tra xem nó đã được cài đặt hay chưa, hãy mở dấu nhắc lệnh và nhập Python như sau:

Bạn cũng có thể kiểm tra điều này trong video bài giảng chi tiết tạihttps://www.tutorialspoint.com/python_essentials_online_training/getting_started_with_anaconda.asp.
Tại sao sử dụng Python cho Khoa học Dữ liệu?
Python là ngôn ngữ quan trọng thứ năm cũng như ngôn ngữ phổ biến nhất cho Máy học và khoa học dữ liệu. Sau đây là các tính năng của Python khiến nó trở thành ngôn ngữ được ưu tiên lựa chọn cho khoa học dữ liệu -
Bộ gói mở rộng
Python có một tập hợp các gói mở rộng và mạnh mẽ, sẵn sàng được sử dụng trong các miền khác nhau. Nó cũng có các gói như numpy, scipy, pandas, scikit-learning, v.v. được yêu cầu cho máy học và khoa học dữ liệu.
Tạo mẫu dễ dàng
Một tính năng quan trọng khác của Python khiến nó trở thành ngôn ngữ được lựa chọn cho khoa học dữ liệu là tạo mẫu dễ dàng và nhanh chóng. Tính năng này rất hữu ích cho việc phát triển thuật toán mới.
Tính năng cộng tác
Lĩnh vực khoa học dữ liệu về cơ bản cần sự hợp tác tốt và Python cung cấp nhiều công cụ hữu ích giúp làm được điều này.
Một ngôn ngữ cho nhiều miền
Một dự án khoa học dữ liệu điển hình bao gồm các lĩnh vực khác nhau như trích xuất dữ liệu, thao tác dữ liệu, phân tích dữ liệu, trích xuất tính năng, mô hình hóa, đánh giá, triển khai và cập nhật giải pháp. Vì Python là một ngôn ngữ đa mục đích, nó cho phép nhà khoa học dữ liệu giải quyết tất cả các miền này từ một nền tảng chung.
Các thành phần của Hệ sinh thái Python ML
Trong phần này, chúng ta hãy thảo luận về một số thư viện Khoa học Dữ liệu cốt lõi hình thành các thành phần của hệ sinh thái Máy học Python. Những thành phần hữu ích này làm cho Python trở thành một ngôn ngữ quan trọng cho Khoa học dữ liệu. Mặc dù có nhiều thành phần như vậy, chúng ta hãy thảo luận một số thành phần quan trọng của hệ sinh thái Python tại đây -
Máy tính xách tay Jupyter
Máy tính xách tay Jupyter về cơ bản cung cấp môi trường tính toán tương tác để phát triển các ứng dụng Khoa học dữ liệu dựa trên Python. Chúng trước đây được gọi là máy tính xách tay ipython. Sau đây là một số tính năng của sổ ghi chép Jupyter khiến nó trở thành một trong những thành phần tốt nhất của hệ sinh thái Python ML:
Máy tính xách tay Jupyter có thể minh họa quá trình phân tích từng bước bằng cách sắp xếp các thứ như mã, hình ảnh, văn bản, kết quả đầu ra, v.v. theo cách từng bước.
Nó giúp một nhà khoa học dữ liệu ghi lại quá trình suy nghĩ trong khi phát triển quá trình phân tích.
Người ta cũng có thể ghi lại kết quả như một phần của sổ ghi chép.
Với sự trợ giúp của sổ ghi chép jupyter, chúng tôi cũng có thể chia sẻ công việc của mình với một người ngang hàng.
Cài đặt và Thực hiện
Nếu bạn đang sử dụng phân phối Anaconda, thì bạn không cần cài đặt riêng sổ ghi chép jupyter vì nó đã được cài đặt với nó. Bạn chỉ cần vào Anaconda Prompt và gõ lệnh sau:
C:\>jupyter notebookSau khi nhấn enter, nó sẽ khởi động máy chủ sổ ghi chép tại localhost: 8888 của máy tính của bạn. Nó được hiển thị trong ảnh chụp màn hình sau:

Bây giờ, sau khi nhấp vào tab Mới, bạn sẽ nhận được danh sách các tùy chọn. Chọn Python 3 và nó sẽ đưa bạn đến sổ ghi chép mới để bắt đầu làm việc với nó. Bạn sẽ thấy nó trong các ảnh chụp màn hình sau:


Mặt khác, nếu bạn đang sử dụng phân phối Python tiêu chuẩn thì sổ ghi chép jupyter có thể được cài đặt bằng trình cài đặt gói python phổ biến, pip.
pip install jupyterCác loại ô trong Máy tính xách tay Jupyter
Sau đây là ba loại ô trong sổ ghi chép jupyter -
Code cells- Đúng như tên gọi, chúng ta có thể sử dụng các ô này để viết mã. Sau khi viết mã / nội dung, nó sẽ gửi nó đến hạt nhân được liên kết với sổ ghi chép.
Markdown cells- Chúng ta có thể sử dụng các ô này để ghi chú quá trình tính toán. Chúng có thể chứa những thứ như văn bản, hình ảnh, phương trình Latex, thẻ HTML, v.v.
Raw cells- Văn bản được viết trong chúng được hiển thị như nó vốn có. Các ô này về cơ bản được sử dụng để thêm văn bản mà chúng tôi không muốn được chuyển đổi bằng cơ chế chuyển đổi tự động của jupyter notebook.
Để nghiên cứu chi tiết hơn về jupyter notebook, bạn có thể vào linkhttps://www.tutorialspoint.com/jupyter/index.htm.
NumPy
Đó là một thành phần hữu ích khác khiến Python trở thành một trong những ngôn ngữ yêu thích cho Khoa học dữ liệu. Về cơ bản, nó là viết tắt của Numerical Python và bao gồm các đối tượng mảng đa chiều. Bằng cách sử dụng NumPy, chúng ta có thể thực hiện các thao tác quan trọng sau:
Các phép toán toán học và logic trên mảng.
Biến đổi Fourier
Các phép toán kết hợp với đại số tuyến tính.
Chúng ta cũng có thể xem NumPy là sự thay thế của MatLab vì NumPy chủ yếu được sử dụng cùng với Scipy (Python khoa học) và Mat-plotlib (thư viện vẽ đồ thị).
Installation and Execution
Nếu bạn đang sử dụng phân phối Anaconda, thì không cần cài đặt NumPy riêng vì nó đã được cài đặt sẵn. Bạn chỉ cần nhập gói vào tập lệnh Python của mình với sự trợ giúp của các bước sau:
import numpy as npMặt khác, nếu bạn đang sử dụng phân phối Python tiêu chuẩn thì NumPy có thể được cài đặt bằng trình cài đặt gói python phổ biến, pip.
pip install NumPyĐể nghiên cứu chi tiết hơn về NumPy, bạn có thể vào liên kếthttps://www.tutorialspoint.com/numpy/index.htm.
Gấu trúc
Đó là một thư viện Python hữu ích khác khiến Python trở thành một trong những ngôn ngữ yêu thích cho Khoa học dữ liệu. Gấu trúc về cơ bản được sử dụng để thao tác, quấn và phân tích dữ liệu. Nó được phát triển bởi Wes McKinney vào năm 2008. Với sự trợ giúp của Pandas, trong quá trình xử lý dữ liệu, chúng ta có thể thực hiện năm bước sau:
Load
Prepare
Manipulate
Model
Analyze
Biểu diễn dữ liệu trong Pandas
Toàn bộ biểu diễn dữ liệu trong Pandas được thực hiện với sự trợ giúp của ba cấu trúc dữ liệu sau:
Series- Về cơ bản nó là một ndarray một chiều với nhãn trục có nghĩa là nó giống như một mảng đơn giản với dữ liệu đồng nhất. Ví dụ: chuỗi sau là tập hợp các số nguyên 1,5,10,15,24,25…
| 1 | 5 | 10 | 15 | 24 | 25 | 28 | 36 | 40 | 89 |
Data frame- Đây là cấu trúc dữ liệu hữu ích nhất và được sử dụng cho hầu hết các loại biểu diễn và thao tác dữ liệu ở gấu trúc. Về cơ bản nó là một cấu trúc dữ liệu hai chiều có thể chứa dữ liệu không đồng nhất. Nói chung, dữ liệu dạng bảng được biểu diễn bằng cách sử dụng các khung dữ liệu. Ví dụ: bảng sau đây cho thấy dữ liệu về các học sinh có tên và số cuộn, tuổi và giới tính -
Tên |
Số cuộn |
Tuổi tác |
Giới tính |
|---|---|---|---|
Aarav |
1 |
15 |
Nam giới |
Nhảm nhí |
2 |
14 |
Nam giới |
Kanika |
3 |
16 |
Giống cái |
Mayank |
4 |
15 |
Nam giới |
Panel- Là cấu trúc dữ liệu 3 chiều chứa dữ liệu không đồng nhất. Rất khó để biểu diễn bảng điều khiển dưới dạng biểu diễn đồ họa, nhưng nó có thể được minh họa như một vùng chứa DataFrame.
Bảng sau đây cho chúng ta thứ nguyên và mô tả về cấu trúc dữ liệu được đề cập ở trên được sử dụng trong Pandas -
Cấu trúc dữ liệu |
Kích thước |
Sự miêu tả |
|---|---|---|
Loạt |
1-D |
Kích thước không thay đổi, dữ liệu đồng nhất 1-D |
DataFrames |
2-D |
Kích thước có thể thay đổi, dữ liệu không đồng nhất ở dạng bảng |
Bảng điều khiển |
3-D |
Mảng có thể thay đổi kích thước, vùng chứa DataFrame. |
Chúng ta có thể hiểu các cấu trúc dữ liệu này là cấu trúc dữ liệu chiều cao hơn là nơi chứa cấu trúc dữ liệu chiều thấp hơn.
Cài đặt và Thực hiện
Nếu bạn đang sử dụng phân phối Anaconda, thì không cần cài đặt riêng Pandas vì nó đã được cài đặt sẵn. Bạn chỉ cần nhập gói vào tập lệnh Python của mình với sự trợ giúp của các bước sau:
import pandas as pdMặt khác, nếu bạn đang sử dụng phân phối Python chuẩn thì Pandas có thể được cài đặt bằng trình cài đặt gói python phổ biến, pip.
pip install PandasSau khi cài đặt Pandas, bạn có thể nhập nó vào tập lệnh Python của mình như đã làm ở trên.
Thí dụ
Sau đây là một ví dụ về cách tạo một chuỗi từ ndarray bằng cách sử dụng Pandas:
In [1]: import pandas as pd
In [2]: import numpy as np
In [3]: data = np.array(['g','a','u','r','a','v'])
In [4]: s = pd.Series(data)
In [5]: print (s)
0 g
1 a
2 u
3 r
4 a
5 v
dtype: objectĐể nghiên cứu chi tiết hơn về gấu trúc, bạn có thể vào liên kết https://www.tutorialspoint.com/python_pandas/index.htm.
Scikit-learning
Một thư viện python hữu ích và quan trọng nhất cho Khoa học dữ liệu và học máy bằng Python là Scikit-learning. Sau đây là một số tính năng của Scikit-learning giúp nó trở nên hữu ích -
Nó được xây dựng trên NumPy, SciPy và Matplotlib.
Nó là một mã nguồn mở và có thể được sử dụng lại theo giấy phép BSD.
Nó có thể truy cập được cho tất cả mọi người và có thể được sử dụng lại trong các ngữ cảnh khác nhau.
Một loạt các thuật toán học máy bao gồm các lĩnh vực chính của ML như phân loại, phân cụm, hồi quy, giảm kích thước, lựa chọn mô hình, v.v. có thể được thực hiện với sự trợ giúp của nó.
Cài đặt và Thực hiện
Nếu bạn đang sử dụng bản phân phối Anaconda, thì không cần cài đặt riêng Scikit-learning vì nó đã được cài đặt sẵn. Bạn chỉ cần sử dụng gói vào tập lệnh Python của mình. Ví dụ: với dòng tập lệnh sau, chúng tôi đang nhập tập dữ liệu về bệnh nhân ung thư vú từScikit-learn -
from sklearn.datasets import load_breast_cancerMặt khác, nếu bạn đang sử dụng phân phối Python chuẩn và có NumPy và SciPy thì Scikit-learning có thể được cài đặt bằng cách sử dụng trình cài đặt gói python phổ biến, pip.
pip install -U scikit-learnSau khi cài đặt Scikit-learning, bạn có thể sử dụng nó vào tập lệnh Python của mình như đã làm ở trên.
Có nhiều thuật toán, kỹ thuật và phương pháp ML khác nhau có thể được sử dụng để xây dựng các mô hình giải quyết các vấn đề trong cuộc sống thực bằng cách sử dụng dữ liệu. Trong chương này, chúng ta sẽ thảo luận về các loại phương pháp khác nhau.
Các loại phương pháp khác nhau
Sau đây là các phương pháp ML khác nhau dựa trên một số danh mục rộng:
Dựa trên sự giám sát của con người
Trong quá trình học, một số phương pháp dựa trên sự giám sát của con người như sau:
Supervised Learning
Các thuật toán hoặc phương pháp học có giám sát là các thuật toán ML được sử dụng phổ biến nhất. Phương pháp hoặc thuật toán học tập này lấy mẫu dữ liệu tức là dữ liệu đào tạo và kết quả đầu ra liên quan của nó, tức là nhãn hoặc phản hồi với mỗi mẫu dữ liệu trong quá trình đào tạo.
Mục tiêu chính của thuật toán học có giám sát là tìm hiểu mối liên hệ giữa các mẫu dữ liệu đầu vào và đầu ra tương ứng sau khi thực hiện nhiều phiên bản dữ liệu đào tạo.
Ví dụ, chúng tôi có
x: Biến đầu vào và
Y: Biến đầu ra
Bây giờ, hãy áp dụng một thuật toán để học hàm ánh xạ từ đầu vào đến đầu ra như sau:
Y = f (x)
Bây giờ, mục tiêu chính là xấp xỉ hàm ánh xạ tốt đến mức ngay cả khi chúng ta có dữ liệu đầu vào mới (x), chúng ta có thể dễ dàng dự đoán biến đầu ra (Y) cho dữ liệu đầu vào mới đó.
Nó được gọi là có giám sát bởi vì toàn bộ quá trình học tập có thể được coi như nó đang được giám sát bởi một giáo viên hoặc người giám sát. Ví dụ về thuật toán học máy được giám sát bao gồmDecision tree, Random Forest, KNN, Logistic Regression Vân vân.
Dựa trên các nhiệm vụ ML, các thuật toán học tập có giám sát có thể được chia thành hai lớp sau:
Classification
Regression
Classification
Mục tiêu chính của các nhiệm vụ dựa trên phân loại là dự đoán các nhãn đầu ra phân loại hoặc phản hồi cho dữ liệu đầu vào nhất định. Đầu ra sẽ dựa trên những gì mô hình đã học được trong giai đoạn đào tạo. Như chúng ta biết rằng các phản hồi đầu ra phân loại có nghĩa là các giá trị không có thứ tự và rời rạc, do đó mỗi phản hồi đầu ra sẽ thuộc về một lớp hoặc danh mục cụ thể. Chúng ta cũng sẽ thảo luận chi tiết về Phân loại và các thuật toán liên quan trong các chương sắp tới.
Regression
Mục tiêu chính của các tác vụ dựa trên hồi quy là dự đoán các nhãn hoặc phản hồi đầu ra là các giá trị số tiếp tục, cho dữ liệu đầu vào đã cho. Đầu ra sẽ dựa trên những gì mô hình đã học được trong giai đoạn đào tạo của nó. Về cơ bản, các mô hình hồi quy sử dụng các đặc trưng dữ liệu đầu vào (các biến độc lập) và các giá trị đầu ra số liên tục tương ứng của chúng (biến phụ thuộc hoặc kết quả) để tìm hiểu mối liên hệ cụ thể giữa đầu vào và đầu ra tương ứng. Chúng tôi cũng sẽ thảo luận chi tiết về hồi quy và các thuật toán liên quan trong các chương tiếp theo.
Học tập không giám sát
Như tên cho thấy, nó đối lập với các phương pháp hoặc thuật toán ML có giám sát, có nghĩa là trong các thuật toán học máy không được giám sát, chúng tôi không có bất kỳ người giám sát nào để cung cấp bất kỳ loại hướng dẫn nào. Các thuật toán học tập không giám sát rất hữu ích trong trường hợp chúng ta không có quyền tự do, giống như trong các thuật toán học tập có giám sát, có dữ liệu đào tạo được gắn nhãn trước và chúng ta muốn trích xuất mẫu hữu ích từ dữ liệu đầu vào.
Ví dụ, có thể hiểu như sau:
Giả sử chúng ta có -
x: Input variables, khi đó sẽ không có biến đầu ra tương ứng và các thuật toán cần khám phá ra mô hình thú vị trong dữ liệu để học.
Ví dụ về các thuật toán học máy không được giám sát bao gồm phân cụm K-mean, K-nearest neighbors Vân vân.
Dựa trên các nhiệm vụ ML, các thuật toán học tập không giám sát có thể được chia thành các lớp rộng sau:
Clustering
Association
Giảm kích thước
Clustering
Các phương pháp phân cụm là một trong những phương pháp ML không giám sát hữu ích nhất. Các thuật toán này được sử dụng để tìm sự giống nhau cũng như các mẫu mối quan hệ giữa các mẫu dữ liệu và sau đó phân cụm các mẫu đó thành các nhóm có sự tương đồng dựa trên các tính năng. Ví dụ thực tế về phân nhóm là nhóm các khách hàng theo hành vi mua hàng của họ.
Association
Một phương pháp ML không giám sát hữu ích khác là Associationđược sử dụng để phân tích tập dữ liệu lớn để tìm ra các mẫu biểu thị thêm các mối quan hệ thú vị giữa các mục khác nhau. Nó cũng được gọi làAssociation Rule Mining hoặc là Market basket analysis được sử dụng chủ yếu để phân tích các mô hình mua sắm của khách hàng.
Dimensionality Reduction
Phương pháp ML không giám sát này được sử dụng để giảm số lượng biến đặc trưng cho mỗi mẫu dữ liệu bằng cách chọn tập hợp các đặc trưng chính hoặc đại diện. Một câu hỏi được đặt ra ở đây là tại sao chúng ta cần giảm kích thước? Lý do đằng sau là vấn đề phức tạp về không gian đối tượng nảy sinh khi chúng tôi bắt đầu phân tích và trích xuất hàng triệu đối tượng từ các mẫu dữ liệu. Vấn đề này thường đề cập đến "lời nguyền về chiều". PCA (Phân tích thành phần chính), K-láng giềng gần nhất và phân tích phân biệt là một số thuật toán phổ biến cho mục đích này.
Anomaly Detection
Phương pháp ML không giám sát này được sử dụng để tìm ra sự xuất hiện của các sự kiện hiếm gặp hoặc quan sát thường không xảy ra. Bằng cách sử dụng kiến thức đã học, các phương pháp phát hiện điểm bất thường sẽ có thể phân biệt điểm dữ liệu bất thường hay điểm bình thường. Một số thuật toán không được giám sát như phân cụm, KNN có thể phát hiện sự bất thường dựa trên dữ liệu và các tính năng của nó.
Học tập bán giám sát
Các loại thuật toán hoặc phương pháp như vậy không được giám sát đầy đủ hoặc không được giám sát hoàn toàn. Về cơ bản chúng nằm giữa hai phương pháp học có giám sát và không giám sát. Các loại thuật toán này thường sử dụng thành phần học tập có giám sát nhỏ, tức là một lượng nhỏ dữ liệu được chú thích được gắn nhãn trước và thành phần học tập không được giám sát lớn tức là rất nhiều dữ liệu không được gắn nhãn để huấn luyện. Chúng ta có thể làm theo bất kỳ phương pháp nào sau đây để triển khai phương pháp học bán giám sát -
Cách tiếp cận đầu tiên và đơn giản là xây dựng mô hình được giám sát dựa trên một lượng nhỏ dữ liệu được gắn nhãn và chú thích, sau đó xây dựng mô hình không được giám sát bằng cách áp dụng điều tương tự cho một lượng lớn dữ liệu không được gắn nhãn để có được nhiều mẫu được gắn nhãn hơn. Bây giờ, đào tạo mô hình trên chúng và lặp lại quy trình.
- , p> Cách tiếp cận thứ hai cần thêm một số nỗ lực. Trong cách tiếp cận này, trước tiên chúng ta có thể sử dụng các phương pháp không được giám sát để phân cụm các mẫu dữ liệu tương tự, chú thích các nhóm này và sau đó sử dụng kết hợp thông tin này để đào tạo mô hình.
Học tăng cường
Các phương pháp này khác với các phương pháp đã nghiên cứu trước đây và cũng rất hiếm khi được sử dụng. Trong loại thuật toán học tập này, sẽ có một tác nhân mà chúng tôi muốn đào tạo trong một khoảng thời gian để nó có thể tương tác với một môi trường cụ thể. Tác nhân sẽ tuân theo một tập hợp các chiến lược để tương tác với môi trường và sau đó sau khi quan sát môi trường, tác nhân sẽ thực hiện các hành động liên quan đến tình trạng hiện tại của môi trường. Sau đây là các bước chính của phương pháp học củng cố -
Step1 - Đầu tiên, chúng ta cần chuẩn bị cho đại lý một số chiến lược đặt ra ban đầu.
Step2 - Sau đó quan sát môi trường và hiện trạng của nó.
Step3 - Tiếp theo, chọn chính sách tối ưu liên quan đến tình trạng hiện tại của môi trường và thực hiện hành động quan trọng.
Step4 - Bây giờ, đại lý có thể nhận được phần thưởng hoặc hình phạt tương ứng theo hành động của nó ở bước trước.
Step5 - Bây giờ, chúng tôi có thể cập nhật các chiến lược nếu nó được yêu cầu.
Step6 - Cuối cùng, lặp lại các bước 2-5 cho đến khi đại lý tìm hiểu và áp dụng các chính sách tối ưu.
Các nhiệm vụ phù hợp với học máy
Sơ đồ sau đây cho thấy loại nhiệm vụ nào thích hợp cho các vấn đề ML khác nhau -

Dựa trên khả năng học tập
Trong quá trình học, sau đây là một số phương pháp dựa trên năng lực học tập -
Batch Learning
Trong nhiều trường hợp, chúng tôi có các hệ thống Học máy end-to-end trong đó chúng tôi cần đào tạo mô hình trong một lần bằng cách sử dụng toàn bộ dữ liệu đào tạo có sẵn. Loại phương pháp học hoặc thuật toán như vậy được gọi làBatch or Offline learning. Nó được gọi là học Batch hoặc Offline vì nó là một thủ tục một lần và mô hình sẽ được đào tạo với dữ liệu trong một đợt duy nhất. Sau đây là các bước chính của phương pháp học theo lô -
Step1 - Đầu tiên, chúng ta cần thu thập tất cả dữ liệu huấn luyện để bắt đầu huấn luyện mô hình.
Step2 - Bây giờ, hãy bắt đầu đào tạo mô hình bằng cách cung cấp toàn bộ dữ liệu đào tạo trong một lần.
Step3 - Tiếp theo, dừng quá trình học tập / đào tạo khi bạn đã đạt được kết quả / hiệu suất làm việc đạt yêu cầu.
Step4- Cuối cùng là triển khai mô hình đã được đào tạo này vào sản xuất. Tại đây, nó sẽ dự đoán đầu ra cho mẫu dữ liệu mới.
Học trực tuyến
Nó hoàn toàn ngược lại với phương pháp học theo lô hay học offline. Trong các phương pháp học tập này, dữ liệu huấn luyện được cung cấp theo nhiều lô tăng dần, được gọi là lô nhỏ, cho thuật toán. Sau đây là các bước chính của phương pháp học Online -
Step1 - Đầu tiên, chúng ta cần thu thập tất cả các dữ liệu huấn luyện để bắt đầu huấn luyện mô hình.
Step2 - Bây giờ, hãy bắt đầu đào tạo mô hình bằng cách cung cấp một lô nhỏ dữ liệu đào tạo cho thuật toán.
Step3 - Tiếp theo, chúng ta cần cung cấp các lô nhỏ dữ liệu huấn luyện theo nhiều bước cho thuật toán.
Step4 - Vì nó sẽ không dừng lại giống như học theo lô, do đó sau khi cung cấp toàn bộ dữ liệu đào tạo trong các lô nhỏ, hãy cung cấp các mẫu dữ liệu mới cho nó.
Step5 - Cuối cùng, nó sẽ tiếp tục học hỏi trong một khoảng thời gian dựa trên các mẫu dữ liệu mới.
Dựa trên Cách tiếp cận Tổng quát
Trong quá trình học, sau đây là một số phương pháp dựa trên cách tiếp cận tổng quát hóa:
Học tập dựa trên phiên bản
Phương pháp học tập dựa trên phiên bản là một trong những phương pháp hữu ích để xây dựng các mô hình ML bằng cách tổng quát hóa dựa trên dữ liệu đầu vào. Nó đối lập với các phương pháp học tập đã nghiên cứu trước đây ở chỗ loại học tập này liên quan đến các hệ thống ML cũng như các phương pháp sử dụng chính các điểm dữ liệu thô để rút ra kết quả cho các mẫu dữ liệu mới hơn mà không cần xây dựng một mô hình rõ ràng về dữ liệu đào tạo.
Nói một cách dễ hiểu, học dựa trên phiên bản về cơ bản bắt đầu hoạt động bằng cách xem xét các điểm dữ liệu đầu vào và sau đó sử dụng một số liệu tương tự, nó sẽ khái quát hóa và dự đoán các điểm dữ liệu mới.
Học tập dựa trên mô hình
Trong phương pháp học dựa trên mô hình, một quá trình lặp lại diễn ra trên các mô hình ML được xây dựng dựa trên các tham số mô hình khác nhau, được gọi là siêu tham số và trong đó dữ liệu đầu vào được sử dụng để trích xuất các tính năng. Trong bài học này, các siêu tham số được tối ưu hóa dựa trên các kỹ thuật xác nhận mô hình khác nhau. Đó là lý do tại sao chúng ta có thể nói rằng phương pháp học tập dựa trên Mô hình sử dụng cách tiếp cận ML truyền thống hơn theo hướng tổng quát hóa.
Giả sử nếu bạn muốn bắt đầu một dự án ML thì điều đầu tiên và quan trọng nhất mà bạn yêu cầu là gì? Đó là dữ liệu mà chúng tôi cần tải để bắt đầu bất kỳ dự án ML nào. Đối với dữ liệu, định dạng dữ liệu phổ biến nhất cho các dự án ML là CSV (các giá trị được phân tách bằng dấu phẩy).
Về cơ bản, CSV là một định dạng tệp đơn giản được sử dụng để lưu trữ dữ liệu dạng bảng (số và văn bản) chẳng hạn như bảng tính ở dạng văn bản thuần túy. Trong Python, chúng ta có thể tải dữ liệu CSV vào bằng nhiều cách khác nhau nhưng trước khi tải dữ liệu CSV, chúng ta phải quan tâm đến một số cân nhắc.
Cân nhắc khi tải dữ liệu CSV
Định dạng dữ liệu CSV là định dạng phổ biến nhất cho dữ liệu ML, nhưng chúng tôi cần quan tâm đến việc thực hiện các cân nhắc chính sau khi tải dữ liệu tương tự vào các dự án ML của chúng tôi -
Tiêu đề tệp
Trong tệp dữ liệu CSV, tiêu đề chứa thông tin cho từng trường. Chúng ta phải sử dụng cùng một dấu phân tách cho tệp tiêu đề và tệp dữ liệu vì tệp tiêu đề chỉ định cách các trường dữ liệu được diễn giải.
Sau đây là hai trường hợp liên quan đến tiêu đề tệp CSV phải được xem xét:
Case-I: When Data file is having a file header - Nó sẽ tự động gán tên cho từng cột dữ liệu nếu tệp dữ liệu có tiêu đề tệp.
Case-II: When Data file is not having a file header - Chúng ta cần gán tên cho từng cột dữ liệu theo cách thủ công nếu tệp dữ liệu không có tiêu đề tệp.
Trong cả hai trường hợp, chúng tôi phải chỉ định rõ ràng thời tiết tệp CSV của chúng tôi có chứa tiêu đề hay không.
Bình luận
Nhận xét trong bất kỳ tệp dữ liệu nào cũng có ý nghĩa quan trọng. Trong tệp dữ liệu CSV, nhận xét được biểu thị bằng dấu thăng (#) ở đầu dòng. Chúng tôi cần xem xét các nhận xét khi tải dữ liệu CSV vào các dự án ML vì nếu chúng tôi có nhận xét trong tệp thì chúng tôi có thể cần chỉ ra, tùy thuộc vào phương pháp chúng tôi chọn để tải, có mong đợi những nhận xét đó hay không.
Dấu phân cách
Trong tệp dữ liệu CSV, ký tự dấu phẩy (,) là dấu phân cách chuẩn. Vai trò của dấu phân cách là phân tách các giá trị trong các trường. Điều quan trọng là phải xem xét vai trò của dấu phân cách trong khi tải tệp CSV lên các dự án ML vì chúng tôi cũng có thể sử dụng dấu phân tách khác như tab hoặc khoảng trắng. Nhưng trong trường hợp sử dụng dấu phân cách khác với dấu phân cách chuẩn, chúng ta phải chỉ định nó một cách rõ ràng.
Báo giá
Trong tệp dữ liệu CSV, dấu ngoặc kép (“”) là ký tự trích dẫn mặc định. Điều quan trọng là phải xem xét vai trò của dấu ngoặc kép trong khi tải tệp CSV lên các dự án ML vì chúng ta cũng có thể sử dụng ký tự trích dẫn khác ngoài dấu ngoặc kép. Nhưng trong trường hợp sử dụng một ký tự trích dẫn khác với ký tự tiêu chuẩn, chúng ta phải chỉ định nó một cách rõ ràng.
Phương pháp tải tệp dữ liệu CSV
Trong khi làm việc với các dự án ML, nhiệm vụ quan trọng nhất là tải dữ liệu đúng cách vào đó. Định dạng dữ liệu phổ biến nhất cho các dự án ML là CSV và nó có nhiều loại khác nhau và khó phân tích cú pháp khác nhau. Trong phần này, chúng ta sẽ thảo luận về ba cách tiếp cận phổ biến trong Python để tải tệp dữ liệu CSV -
Tải CSV bằng Thư viện chuẩn Python
Cách tiếp cận đầu tiên và được sử dụng nhiều nhất để tải tệp dữ liệu CSV là sử dụng thư viện chuẩn Python, cung cấp cho chúng ta nhiều mô-đun tích hợp cụ thể là mô-đun csv và hàm reader (). Sau đây là một ví dụ về tải tệp dữ liệu CSV với sự trợ giúp của nó:
Thí dụ
Trong ví dụ này, chúng tôi đang sử dụng tập dữ liệu hoa iris có thể được tải xuống thư mục cục bộ của chúng tôi. Sau khi tải tệp dữ liệu, chúng ta có thể chuyển đổi nó thành mảng NumPy và sử dụng nó cho các dự án ML. Sau đây là tập lệnh Python để tải tệp dữ liệu CSV:
Đầu tiên, chúng ta cần nhập mô-đun csv được cung cấp bởi thư viện chuẩn Python như sau:
import csvTiếp theo, chúng ta cần nhập mô-đun Numpy để chuyển đổi dữ liệu đã tải thành mảng NumPy.
import numpy as npBây giờ, hãy cung cấp đường dẫn đầy đủ của tệp, được lưu trữ trên thư mục cục bộ của chúng tôi, có tệp dữ liệu CSV -
path = r"c:\iris.csv"Tiếp theo, sử dụng hàm csv.reader () để đọc dữ liệu từ tệp CSV -
with open(path,'r') as f:
reader = csv.reader(f,delimiter = ',')
headers = next(reader)
data = list(reader)
data = np.array(data).astype(float)Chúng ta có thể in tên của các tiêu đề với dòng tập lệnh sau:
print(headers)Dòng lệnh sau sẽ in ra hình dạng của dữ liệu, tức là số hàng & cột trong tệp:
print(data.shape)Dòng script tiếp theo sẽ cung cấp ba dòng đầu tiên của tệp dữ liệu -
print(data[:3])Output
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
(150, 4)
[ [5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]]Tải CSV bằng NumPy
Một cách tiếp cận khác để tải tệp dữ liệu CSV là hàm NumPy và numpy.loadtxt (). Sau đây là một ví dụ về tải tệp dữ liệu CSV với sự trợ giúp của nó:
Thí dụ
Trong ví dụ này, chúng tôi đang sử dụng Tập dữ liệu Pima Indians có dữ liệu về bệnh nhân tiểu đường. Tập dữ liệu này là tập dữ liệu số không có tiêu đề. Nó cũng có thể được tải xuống thư mục cục bộ của chúng tôi. Sau khi tải tệp dữ liệu, chúng ta có thể chuyển đổi nó thành mảng NumPy và sử dụng nó cho các dự án ML. Sau đây là tập lệnh Python để tải tệp dữ liệu CSV:
from numpy import loadtxt
path = r"C:\pima-indians-diabetes.csv"
datapath= open(path, 'r')
data = loadtxt(datapath, delimiter=",")
print(data.shape)
print(data[:3])Đầu ra
(768, 9)
[ [ 6. 148. 72. 35. 0. 33.6 0.627 50. 1.]
[ 1. 85. 66. 29. 0. 26.6 0.351 31. 0.]
[ 8. 183. 64. 0. 0. 23.3 0.672 32. 1.]]Tải CSV bằng Gấu trúc
Một cách tiếp cận khác để tải tệp dữ liệu CSV là bằng hàm Pandas và pandas.read_csv (). Đây là hàm rất linh hoạt trả về một pandas.DataFrame có thể được sử dụng ngay lập tức để vẽ biểu đồ. Sau đây là một ví dụ về tải tệp dữ liệu CSV với sự trợ giúp của nó:
Thí dụ
Ở đây, chúng tôi sẽ triển khai hai tập lệnh Python, đầu tiên là với tập dữ liệu Iris có tiêu đề và một tập lệnh khác là sử dụng Tập dữ liệu Pima Indians, là tập dữ liệu số không có tiêu đề. Cả hai bộ dữ liệu có thể được tải xuống thư mục cục bộ.
Script-1
Sau đây là tập lệnh Python để tải tệp dữ liệu CSV bằng Pandas trên Iris Data set:
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.shape)
print(data[:3])
Output:
(150, 4)
sepal_length sepal_width petal_length petal_width
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2Script-2
Sau đây là tập lệnh Python để tải tệp dữ liệu CSV, cùng với việc cung cấp tên tiêu đề, bằng cách sử dụng Pandas trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima -
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
print(data.shape)
print(data[:3])Output
(768, 9)
preg plas pres skin test mass pedi age class
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1Có thể dễ dàng hiểu được sự khác biệt giữa ba cách tiếp cận đã sử dụng ở trên để tải tệp dữ liệu CSV với sự trợ giúp của các ví dụ đã cho.
Giới thiệu
Trong khi làm việc với các dự án máy học, chúng tôi thường bỏ qua hai phần quan trọng nhất được gọi là mathematics và data. Đó là bởi vì, chúng tôi biết rằng ML là một cách tiếp cận theo hướng dữ liệu và mô hình ML của chúng tôi sẽ chỉ tạo ra kết quả tốt hoặc xấu như dữ liệu chúng tôi cung cấp cho nó.
Trong chương trước, chúng ta đã thảo luận về cách chúng ta có thể tải dữ liệu CSV lên dự án ML của mình, nhưng sẽ rất tốt nếu bạn hiểu dữ liệu trước khi tải lên. Chúng ta có thể hiểu dữ liệu bằng hai cách, bằng số liệu thống kê và bằng trực quan.
Trong chương này, với sự trợ giúp của các công thức Python sau đây, chúng ta sẽ hiểu dữ liệu ML với số liệu thống kê.
Nhìn vào dữ liệu thô
Công thức đầu tiên là xem xét dữ liệu thô của bạn. Điều quan trọng là phải xem dữ liệu thô bởi vì cái nhìn sâu sắc chúng ta sẽ có được sau khi xem dữ liệu thô sẽ thúc đẩy cơ hội của chúng ta để xử lý trước cũng như xử lý dữ liệu tốt hơn cho các dự án ML.
Sau đây là một tập lệnh Python được triển khai bằng cách sử dụng hàm head () của Pandas DataFrame trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima để xem xét 50 hàng đầu tiên để hiểu rõ hơn về nó -
Thí dụ
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
print(data.head(50))Đầu ra
preg plas pres skin test mass pedi age class
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1
5 5 116 74 0 0 25.6 0.201 30 0
6 3 78 50 32 88 31.0 0.248 26 1
7 10 115 0 0 0 35.3 0.134 29 0
8 2 197 70 45 543 30.5 0.158 53 1
9 8 125 96 0 0 0.0 0.232 54 1
10 4 110 92 0 0 37.6 0.191 30 0
11 10 168 74 0 0 38.0 0.537 34 1
12 10 139 80 0 0 27.1 1.441 57 0
13 1 189 60 23 846 30.1 0.398 59 1
14 5 166 72 19 175 25.8 0.587 51 1
15 7 100 0 0 0 30.0 0.484 32 1
16 0 118 84 47 230 45.8 0.551 31 1
17 7 107 74 0 0 29.6 0.254 31 1
18 1 103 30 38 83 43.3 0.183 33 0
19 1 115 70 30 96 34.6 0.529 32 1
20 3 126 88 41 235 39.3 0.704 27 0
21 8 99 84 0 0 35.4 0.388 50 0
22 7 196 90 0 0 39.8 0.451 41 1
23 9 119 80 35 0 29.0 0.263 29 1
24 11 143 94 33 146 36.6 0.254 51 1
25 10 125 70 26 115 31.1 0.205 41 1
26 7 147 76 0 0 39.4 0.257 43 1
27 1 97 66 15 140 23.2 0.487 22 0
28 13 145 82 19 110 22.2 0.245 57 0
29 5 117 92 0 0 34.1 0.337 38 0
30 5 109 75 26 0 36.0 0.546 60 0
31 3 158 76 36 245 31.6 0.851 28 1
32 3 88 58 11 54 24.8 0.267 22 0
33 6 92 92 0 0 19.9 0.188 28 0
34 10 122 78 31 0 27.6 0.512 45 0
35 4 103 60 33 192 24.0 0.966 33 0
36 11 138 76 0 0 33.2 0.420 35 0
37 9 102 76 37 0 32.9 0.665 46 1
38 2 90 68 42 0 38.2 0.503 27 1
39 4 111 72 47 207 37.1 1.390 56 1
40 3 180 64 25 70 34.0 0.271 26 0
41 7 133 84 0 0 40.2 0.696 37 0
42 7 106 92 18 0 22.7 0.235 48 0
43 9 171 110 24 240 45.4 0.721 54 1
44 7 159 64 0 0 27.4 0.294 40 0
45 0 180 66 39 0 42.0 1.893 25 1
46 1 146 56 0 0 29.7 0.564 29 0
47 2 71 70 27 0 28.0 0.586 22 0
48 7 103 66 32 0 39.1 0.344 31 1
49 7 105 0 0 0 0.0 0.305 24 0Chúng ta có thể quan sát từ đầu ra ở trên rằng cột đầu tiên cung cấp số hàng có thể rất hữu ích để tham khảo một quan sát cụ thể.
Kiểm tra kích thước dữ liệu
Luôn luôn là một thực tiễn tốt để biết chúng ta đang có bao nhiêu dữ liệu, về hàng và cột cho dự án ML của mình. Những lý do đằng sau là -
Giả sử nếu chúng ta có quá nhiều hàng và cột thì sẽ mất nhiều thời gian để chạy thuật toán và đào tạo mô hình.
Giả sử nếu chúng ta có quá ít hàng và cột thì chúng ta sẽ không có đủ dữ liệu để đào tạo tốt mô hình.
Sau đây là một tập lệnh Python được triển khai bằng cách in thuộc tính hình dạng trên Khung dữ liệu Pandas. Chúng tôi sẽ triển khai nó trên tập dữ liệu iris để lấy tổng số hàng và cột trong đó.
Thí dụ
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.shape)Đầu ra
(150, 4)Chúng ta có thể dễ dàng quan sát từ đầu ra mà tập dữ liệu mống mắt, chúng ta sẽ sử dụng, có 150 hàng và 4 cột.
Nhận kiểu dữ liệu của từng thuộc tính
Một phương pháp hay khác là biết kiểu dữ liệu của từng thuộc tính. Lý do đằng sau là, theo yêu cầu, đôi khi chúng ta có thể cần chuyển đổi một kiểu dữ liệu này sang kiểu dữ liệu khác. Ví dụ: chúng tôi có thể cần chuyển đổi chuỗi thành dấu phẩy động hoặc int để biểu diễn các giá trị phân loại hoặc thứ tự. Chúng ta có thể có ý tưởng về kiểu dữ liệu của thuộc tính bằng cách xem dữ liệu thô, nhưng một cách khác là sử dụng thuộc tính dtypes của Pandas DataFrame. Với sự trợ giúp của thuộc tính dtypes, chúng ta có thể phân loại từng kiểu dữ liệu thuộc tính. Nó có thể được hiểu với sự trợ giúp của tập lệnh Python sau:
Thí dụ
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.dtypes)Đầu ra
sepal_length float64
sepal_width float64
petal_length float64
petal_width float64
dtype: objectTừ kết quả trên, chúng ta có thể dễ dàng nhận được các kiểu dữ liệu của từng thuộc tính.
Tóm tắt thống kê dữ liệu
Chúng ta đã thảo luận về công thức Python để có được hình dạng tức là số hàng và cột, của dữ liệu nhưng nhiều lần chúng ta cần xem lại các tóm tắt từ hình dạng dữ liệu đó. Nó có thể được thực hiện với sự trợ giúp của hàm description () của Pandas DataFrame cung cấp thêm 8 thuộc tính thống kê sau của mỗi & mọi thuộc tính dữ liệu -
Count
Mean
Độ lệch chuẩn
Giá trị tối thiểu
Gia trị lơn nhât
25%
Trung bình tức là 50%
75%
Thí dụ
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
print(data.shape)
print(data.describe())Đầu ra
(768, 9)
preg plas pres skin test mass pedi age class
count 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00
mean 3.85 120.89 69.11 20.54 79.80 31.99 0.47 33.24 0.35
std 3.37 31.97 19.36 15.95 115.24 7.88 0.33 11.76 0.48
min 0.00 0.00 0.00 0.00 0.00 0.00 0.08 21.00 0.00
25% 1.00 99.00 62.00 0.00 0.00 27.30 0.24 24.00 0.00
50% 3.00 117.00 72.00 23.00 30.50 32.00 0.37 29.00 0.00
75% 6.00 140.25 80.00 32.00 127.25 36.60 0.63 41.00 1.00
max 17.00 199.00 122.00 99.00 846.00 67.10 2.42 81.00 1.00Từ kết quả trên, chúng ta có thể quan sát tóm tắt thống kê dữ liệu của bộ dữ liệu bệnh tiểu đường Ấn Độ Pima cùng với hình dạng dữ liệu.
Xem xét phân phối lớp học
Thống kê phân phối lớp rất hữu ích trong các bài toán phân loại nơi chúng ta cần biết số dư của các giá trị lớp. Điều quan trọng là phải biết phân phối giá trị lớp vì nếu chúng ta có phân phối lớp không cân bằng cao, tức là một lớp có nhiều quan sát hơn lớp khác, thì nó có thể cần xử lý đặc biệt ở giai đoạn chuẩn bị dữ liệu của dự án ML của chúng ta. Chúng ta có thể dễ dàng nhận được phân phối lớp bằng Python với sự trợ giúp của Pandas DataFrame.
Thí dụ
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
count_class = data.groupby('class').size()
print(count_class)Đầu ra
Class
0 500
1 268
dtype: int64Từ kết quả trên, có thể thấy rõ rằng số lượng quan sát với lớp 0 gần như gấp đôi số quan sát với lớp 1.
Xem xét mối tương quan giữa các thuộc tính
Mối quan hệ giữa hai biến được gọi là mối tương quan. Trong thống kê, phương pháp phổ biến nhất để tính toán độ tương quan là Hệ số tương quan của Pearson. Nó có thể có ba giá trị như sau:
Coefficient value = 1 - Nó thể hiện đầy đủ positive tương quan giữa các biến.
Coefficient value = -1 - Nó thể hiện đầy đủ negative tương quan giữa các biến.
Coefficient value = 0 - Nó đại diện cho no tương quan giữa các biến.
Chúng tôi luôn luôn tốt khi xem xét các mối tương quan theo cặp của các thuộc tính trong tập dữ liệu của mình trước khi sử dụng nó vào dự án ML vì một số thuật toán học máy như hồi quy tuyến tính và hồi quy logistic sẽ hoạt động kém nếu chúng tôi có các thuộc tính tương quan cao. Trong Python, chúng ta có thể dễ dàng tính toán ma trận tương quan của các thuộc tính tập dữ liệu với sự trợ giúp của hàm corr () trên Pandas DataFrame.
Thí dụ
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
correlations = data.corr(method='pearson')
print(correlations)Đầu ra
preg plas pres skin test mass pedi age class
preg 1.00 0.13 0.14 -0.08 -0.07 0.02 -0.03 0.54 0.22
plas 0.13 1.00 0.15 0.06 0.33 0.22 0.14 0.26 0.47
pres 0.14 0.15 1.00 0.21 0.09 0.28 0.04 0.24 0.07
skin -0.08 0.06 0.21 1.00 0.44 0.39 0.18 -0.11 0.07
test -0.07 0.33 0.09 0.44 1.00 0.20 0.19 -0.04 0.13
mass 0.02 0.22 0.28 0.39 0.20 1.00 0.14 0.04 0.29
pedi -0.03 0.14 0.04 0.18 0.19 0.14 1.00 0.03 0.17
age 0.54 0.26 0.24 -0.11 -0.04 0.04 0.03 1.00 0.24
class 0.22 0.47 0.07 0.07 0.13 0.29 0.17 0.24 1.00Ma trận ở đầu ra ở trên cung cấp mối tương quan giữa tất cả các cặp thuộc tính trong tập dữ liệu.
Xem xét lại phần phân bổ thuộc tính
Độ xiên có thể được định nghĩa là sự phân bố được giả định là Gauss nhưng có vẻ bị bóp méo hoặc dịch chuyển theo hướng này hay hướng khác, hoặc sang trái hoặc phải. Xem xét độ lệch của các thuộc tính là một trong những nhiệm vụ quan trọng do những lý do sau:
Sự hiện diện của độ lệch trong dữ liệu đòi hỏi phải hiệu chỉnh ở giai đoạn chuẩn bị dữ liệu để chúng tôi có thể có được độ chính xác hơn từ mô hình của mình.
Hầu hết các thuật toán ML giả định rằng dữ liệu có phân phối Gaussian tức là chuẩn của dữ liệu cong hình chuông.
Trong Python, chúng ta có thể dễ dàng tính toán độ lệch của từng thuộc tính bằng cách sử dụng hàm xiên () trên Pandas DataFrame.
Thí dụ
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
print(data.skew())Đầu ra
preg 0.90
plas 0.17
pres -1.84
skin 0.11
test 2.27
mass -0.43
pedi 1.92
age 1.13
class 0.64
dtype: float64Từ đầu ra trên, có thể quan sát được độ lệch âm hoặc dương. Nếu giá trị gần bằng 0 thì nó hiển thị ít lệch hơn.
Giới thiệu
Trong chương trước, chúng ta đã thảo luận về tầm quan trọng của dữ liệu đối với các thuật toán Học máy cùng với một số công thức Python để hiểu dữ liệu với số liệu thống kê. Có một cách khác gọi là Visualization, để hiểu dữ liệu.
Với sự trợ giúp của trực quan hóa dữ liệu, chúng ta có thể thấy dữ liệu trông như thế nào và loại tương quan được nắm giữ bởi các thuộc tính của dữ liệu. Đó là cách nhanh nhất để xem các tính năng có tương ứng với đầu ra hay không. Với sự trợ giúp của các công thức Python sau đây, chúng ta có thể hiểu dữ liệu ML với số liệu thống kê.

Các lô đơn lẻ: Hiểu các thuộc tính một cách độc lập
Loại trực quan đơn giản nhất là trực quan một biến hoặc “đơn biến”. Với sự trợ giúp của trực quan hóa đơn biến, chúng ta có thể hiểu từng thuộc tính của tập dữ liệu một cách độc lập. Sau đây là một số kỹ thuật trong Python để triển khai trực quan hóa đơn biến:
Biểu đồ
Biểu đồ nhóm dữ liệu trong các thùng và là cách nhanh nhất để có ý tưởng về sự phân bố của từng thuộc tính trong tập dữ liệu. Sau đây là một số đặc điểm của biểu đồ:
Nó cung cấp cho chúng ta số lượng quan sát trong mỗi thùng được tạo để trực quan hóa.
Từ hình dạng của thùng, chúng ta có thể dễ dàng quan sát sự phân bố tức là thời tiết nó là Gaussian, lệch hoặc hàm mũ.
Biểu đồ cũng giúp chúng ta nhìn thấy các ngoại lệ có thể xảy ra.
Thí dụ
Đoạn mã được hiển thị bên dưới là một ví dụ về tập lệnh Python tạo biểu đồ của các thuộc tính của tập dữ liệu bệnh tiểu đường ở Ấn Độ Pima. Ở đây, chúng tôi sẽ sử dụng hàm hist () trên Pandas DataFrame để tạo biểu đồ vàmatplotlib để khai thác chúng.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.hist()
pyplot.show()Đầu ra
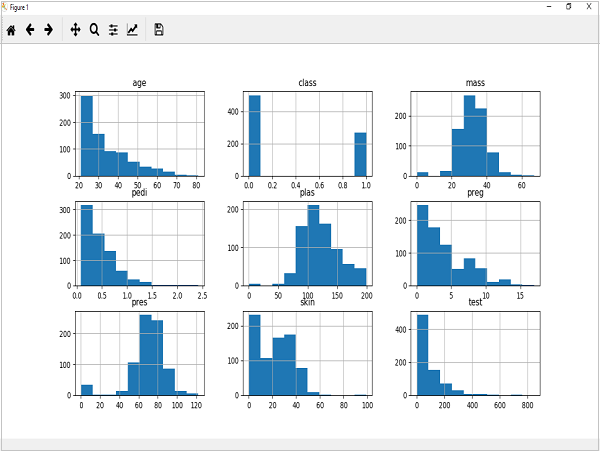
Kết quả trên cho thấy rằng nó đã tạo biểu đồ cho từng thuộc tính trong tập dữ liệu. Từ đó, chúng ta có thể quan sát rằng có lẽ tuổi, pedi và thuộc tính thử nghiệm có thể có phân phối hàm mũ trong khi khối lượng và plas có phân phối Gauss.
Lô mật độ
Một kỹ thuật nhanh chóng và dễ dàng khác để nhận phân phối từng thuộc tính là biểu đồ Mật độ. Nó cũng giống như biểu đồ nhưng có một đường cong mượt mà được vẽ qua đầu mỗi thùng. Chúng ta có thể gọi chúng là biểu đồ trừu tượng.
Thí dụ
Trong ví dụ sau, tập lệnh Python sẽ tạo các Lô mật độ để phân phối các thuộc tính của tập dữ liệu bệnh tiểu đường ở Ấn Độ Pima.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.plot(kind='density', subplots=True, layout=(3,3), sharex=False)
pyplot.show()Đầu ra
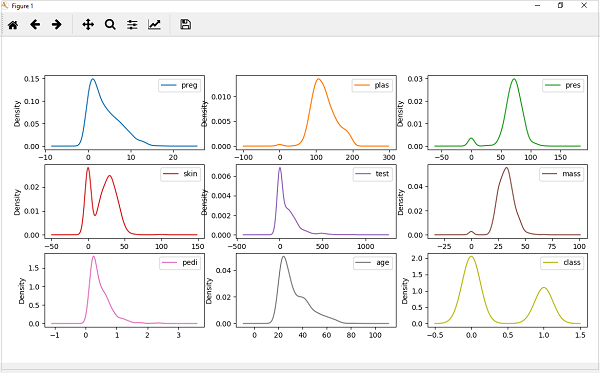
Từ kết quả trên, có thể dễ dàng hiểu được sự khác biệt giữa biểu đồ Mật độ và Biểu đồ.
Hộp và Lô đánh bài
Ô Box và Whisker, còn được gọi ngắn gọn là ô hộp, là một kỹ thuật hữu ích khác để xem xét sự phân bố của mỗi thuộc tính. Sau đây là các đặc điểm của kỹ thuật này:
Nó có bản chất đơn biến và tóm tắt sự phân bố của từng thuộc tính.
Nó vẽ một đường cho giá trị giữa tức là cho giá trị trung bình.
Nó vẽ một hộp xung quanh 25% và 75%.
Nó cũng vẽ những sợi râu sẽ cho chúng ta ý tưởng về sự lan truyền của dữ liệu.
Các dấu chấm bên ngoài râu biểu thị các giá trị ngoại lệ. Giá trị ngoại lai sẽ lớn hơn 1,5 lần so với kích thước của mức độ lan truyền của dữ liệu giữa.
Thí dụ
Trong ví dụ sau, tập lệnh Python sẽ tạo các Lô mật độ để phân phối các thuộc tính của tập dữ liệu bệnh tiểu đường ở Ấn Độ Pima.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.plot(kind='box', subplots=True, layout=(3,3), sharex=False,sharey=False)
pyplot.show()Đầu ra

Từ biểu đồ phân bố của thuộc tính ở trên, có thể quan sát thấy rằng tuổi, thử nghiệm và làn da có vẻ lệch về các giá trị nhỏ hơn.
Lô đa biến: Tương tác giữa nhiều biến
Một kiểu trực quan khác là trực quan đa biến hoặc “đa biến”. Với sự trợ giúp của trực quan hóa đa biến, chúng ta có thể hiểu được sự tương tác giữa nhiều thuộc tính trong tập dữ liệu của mình. Sau đây là một số kỹ thuật trong Python để triển khai trực quan hóa đa biến:
Lô ma trận tương quan
Tương quan là một chỉ báo về những thay đổi giữa hai biến. Trong các chương trước của chúng ta, chúng ta đã thảo luận về hệ số Tương quan của Pearson và tầm quan trọng của Tương quan. Chúng ta có thể vẽ ma trận tương quan để chỉ ra biến nào có mối tương quan cao hay thấp đối với một biến khác.
Thí dụ
Trong ví dụ sau, tập lệnh Python sẽ tạo và vẽ biểu đồ ma trận tương quan cho tập dữ liệu bệnh tiểu đường ở Ấn Độ Pima. Nó có thể được tạo với sự trợ giúp của hàm corr () trên Pandas DataFrame và được vẽ với sự trợ giúp của pyplot.
from matplotlib import pyplot
from pandas import read_csv
import numpy
Path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(Path, names=names)
correlations = data.corr()
fig = pyplot.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(correlations, vmin=-1, vmax=1)
fig.colorbar(cax)
ticks = numpy.arange(0,9,1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
pyplot.show()Đầu ra

Từ đầu ra ở trên của ma trận tương quan, chúng ta có thể thấy rằng nó là đối xứng tức là phía dưới bên trái giống với phía trên bên phải. Người ta cũng quan sát thấy rằng mỗi biến có tương quan thuận với nhau.
Lô ma trận phân tán
Biểu đồ phân tán cho biết mức độ ảnh hưởng của một biến số khác hoặc mối quan hệ giữa chúng với sự trợ giúp của các dấu chấm trong hai chiều. Biểu đồ phân tán rất giống biểu đồ đường theo khái niệm rằng chúng sử dụng các trục ngang và trục dọc để vẽ các điểm dữ liệu.
Thí dụ
Trong ví dụ sau, tập lệnh Python sẽ tạo và vẽ biểu đồ ma trận Phân tán cho tập dữ liệu Bệnh tiểu đường ở Ấn Độ Pima. Nó có thể được tạo với sự trợ giúp của hàm scatter_matrix () trên Pandas DataFrame và được vẽ với sự trợ giúp của pyplot.
from matplotlib import pyplot
from pandas import read_csv
from pandas.tools.plotting import scatter_matrix
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
scatter_matrix(data)
pyplot.show()Đầu ra

Giới thiệu
Các thuật toán Máy học hoàn toàn phụ thuộc vào dữ liệu vì nó là khía cạnh quan trọng nhất giúp đào tạo mô hình có thể thực hiện được. Mặt khác, nếu chúng ta không thể hiểu được dữ liệu đó, trước khi đưa nó vào các thuật toán ML, một cỗ máy sẽ trở nên vô dụng. Nói một cách dễ hiểu, chúng ta luôn cần cung cấp dữ liệu phù hợp, tức là dữ liệu ở đúng tỷ lệ, định dạng và chứa các tính năng có ý nghĩa cho vấn đề chúng ta muốn máy giải quyết.
Điều này làm cho việc chuẩn bị dữ liệu trở thành bước quan trọng nhất trong quy trình ML. Chuẩn bị dữ liệu có thể được định nghĩa là quy trình làm cho tập dữ liệu của chúng tôi phù hợp hơn với quy trình ML.
Tại sao phải xử lý trước dữ liệu?
Sau khi chọn dữ liệu thô cho việc huấn luyện ML, công việc quan trọng nhất là xử lý trước dữ liệu. Theo nghĩa rộng, tiền xử lý dữ liệu sẽ chuyển đổi dữ liệu đã chọn thành một dạng mà chúng ta có thể làm việc hoặc có thể cung cấp cho các thuật toán ML. Chúng tôi luôn cần xử lý trước dữ liệu của mình để dữ liệu có thể giống như kỳ vọng của thuật toán học máy.
Kỹ thuật xử lý trước dữ liệu
Chúng tôi có các kỹ thuật tiền xử lý dữ liệu sau đây có thể được áp dụng trên tập dữ liệu để tạo ra dữ liệu cho các thuật toán ML -
Mở rộng quy mô
Hầu hết có lẽ tập dữ liệu của chúng tôi bao gồm các thuộc tính với tỷ lệ khác nhau, nhưng chúng tôi không thể cung cấp dữ liệu đó cho thuật toán ML do đó nó yêu cầu thay đổi tỷ lệ. Thay đổi tỷ lệ dữ liệu đảm bảo rằng các thuộc tính có cùng tỷ lệ. Nói chung, các thuộc tính được thay đổi tỷ lệ thành phạm vi 0 và 1. Các thuật toán ML như gradient descent và k-Nearest Neighbors yêu cầu dữ liệu được chia tỷ lệ. Chúng tôi có thể bán lại dữ liệu với sự trợ giúp của lớp MinMaxScaler của thư viện Scikit-learning Python.
Thí dụ
Trong ví dụ này, chúng tôi sẽ bán lại dữ liệu của bộ dữ liệu bệnh tiểu đường người da đỏ Pima mà chúng tôi đã sử dụng trước đó. Đầu tiên, dữ liệu CSV sẽ được tải (như đã thực hiện trong các chương trước) và sau đó với sự trợ giúp của lớp MinMaxScaler, nó sẽ được thay đổi tỷ lệ trong phạm vi 0 và 1.
Vài dòng đầu tiên của tập lệnh sau giống như chúng ta đã viết trong các chương trước khi tải dữ liệu CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn import preprocessing
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesBây giờ, chúng ta có thể sử dụng lớp MinMaxScaler để thay đổi tỷ lệ dữ liệu trong phạm vi 0 và 1.
data_scaler = preprocessing.MinMaxScaler(feature_range=(0,1))
data_rescaled = data_scaler.fit_transform(array)Chúng tôi cũng có thể tóm tắt dữ liệu cho đầu ra theo lựa chọn của chúng tôi. Ở đây, chúng tôi đang đặt độ chính xác thành 1 và hiển thị 10 hàng đầu tiên trong đầu ra.
set_printoptions(precision=1)
print ("\nScaled data:\n", data_rescaled[0:10])Đầu ra
Scaled data:
[[0.4 0.7 0.6 0.4 0. 0.5 0.2 0.5 1. ]
[0.1 0.4 0.5 0.3 0. 0.4 0.1 0.2 0. ]
[0.5 0.9 0.5 0. 0. 0.3 0.3 0.2 1. ]
[0.1 0.4 0.5 0.2 0.1 0.4 0. 0. 0. ]
[0. 0.7 0.3 0.4 0.2 0.6 0.9 0.2 1. ]
[0.3 0.6 0.6 0. 0. 0.4 0.1 0.2 0. ]
[0.2 0.4 0.4 0.3 0.1 0.5 0.1 0.1 1. ]
[0.6 0.6 0. 0. 0. 0.5 0. 0.1 0. ]
[0.1 1. 0.6 0.5 0.6 0.5 0. 0.5 1. ]
[0.5 0.6 0.8 0. 0. 0. 0.1 0.6 1. ]]Từ đầu ra ở trên, tất cả dữ liệu đã được thay đổi tỷ lệ thành phạm vi 0 và 1.
Bình thường hóa
Một kỹ thuật tiền xử lý dữ liệu hữu ích khác là Chuẩn hóa. Điều này được sử dụng để bán lại mỗi hàng dữ liệu có độ dài là 1. Nó chủ yếu hữu ích trong tập dữ liệu thưa thớt nơi chúng ta có rất nhiều số không. Chúng ta có thể chia tỷ lệ dữ liệu với sự trợ giúp của lớp Normalizer của thư viện Python scikit-learning.
Các loại chuẩn hóa
Trong học máy, có hai loại kỹ thuật tiền xử lý chuẩn hóa như sau:
Chuẩn hóa L1
Nó có thể được định nghĩa là kỹ thuật chuẩn hóa sửa đổi các giá trị của tập dữ liệu theo cách mà trong mỗi hàng, tổng các giá trị tuyệt đối sẽ luôn bằng 1. Nó còn được gọi là Sai lệch tuyệt đối ít nhất.
Example
Trong ví dụ này, chúng tôi sử dụng kỹ thuật L1 Normalize để chuẩn hóa dữ liệu của bộ dữ liệu bệnh tiểu đường người da đỏ Pima mà chúng tôi đã sử dụng trước đó. Đầu tiên, dữ liệu CSV sẽ được tải và sau đó với sự trợ giúp của lớp Normalizer, nó sẽ được chuẩn hóa.
Vài dòng đầu tiên của tập lệnh sau giống như chúng ta đã viết trong các chương trước khi tải dữ liệu CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv (path, names=names)
array = dataframe.valuesBây giờ, chúng ta có thể sử dụng lớp Normalizer với L1 để chuẩn hóa dữ liệu.
Data_normalizer = Normalizer(norm='l1').fit(array)
Data_normalized = Data_normalizer.transform(array)Chúng tôi cũng có thể tóm tắt dữ liệu cho đầu ra theo lựa chọn của chúng tôi. Ở đây, chúng tôi đang đặt độ chính xác thành 2 và hiển thị 3 hàng đầu tiên trong đầu ra.
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])Output
Normalized data:
[[0.02 0.43 0.21 0.1 0. 0.1 0. 0.14 0. ]
[0. 0.36 0.28 0.12 0. 0.11 0. 0.13 0. ]
[0.03 0.59 0.21 0. 0. 0.07 0. 0.1 0. ]]Chuẩn hóa L2
Nó có thể được định nghĩa là kỹ thuật chuẩn hóa sửa đổi các giá trị của tập dữ liệu theo cách mà trong mỗi hàng, tổng các bình phương sẽ luôn lên đến 1. Nó còn được gọi là bình phương nhỏ nhất.
Example
Trong ví dụ này, chúng tôi sử dụng kỹ thuật Chuẩn hóa L2 để chuẩn hóa dữ liệu của bộ dữ liệu bệnh tiểu đường người da đỏ Pima mà chúng tôi đã sử dụng trước đó. Đầu tiên, dữ liệu CSV sẽ được tải (như đã thực hiện trong các chương trước) và sau đó với sự trợ giúp của lớp Normalizer, nó sẽ được chuẩn hóa.
Vài dòng đầu tiên của tập lệnh sau giống như chúng ta đã viết trong các chương trước khi tải dữ liệu CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv (path, names=names)
array = dataframe.valuesBây giờ, chúng ta có thể sử dụng lớp Normalizer với L1 để chuẩn hóa dữ liệu.
Data_normalizer = Normalizer(norm='l2').fit(array)
Data_normalized = Data_normalizer.transform(array)Chúng tôi cũng có thể tóm tắt dữ liệu cho đầu ra theo lựa chọn của chúng tôi. Ở đây, chúng tôi đang đặt độ chính xác thành 2 và hiển thị 3 hàng đầu tiên trong đầu ra.
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])Output
Normalized data:
[[0.03 0.83 0.4 0.2 0. 0.19 0. 0.28 0.01]
[0.01 0.72 0.56 0.24 0. 0.22 0. 0.26 0. ]
[0.04 0.92 0.32 0. 0. 0.12 0. 0.16 0.01]]Binarization
Như tên cho thấy, đây là kỹ thuật với sự trợ giúp của chúng tôi có thể tạo dữ liệu nhị phân. Chúng tôi có thể sử dụng ngưỡng nhị phân để tạo dữ liệu của chúng tôi thành nhị phân. Các giá trị trên giá trị ngưỡng đó sẽ được chuyển đổi thành 1 và dưới ngưỡng đó sẽ được chuyển đổi thành 0. Ví dụ: nếu chúng ta chọn giá trị ngưỡng = 0,5, thì giá trị tập dữ liệu trên nó sẽ trở thành 1 và dưới ngưỡng này sẽ trở thành 0. Nghĩa là tại sao chúng ta có thể gọi nóbinarizing dữ liệu hoặc thresholdingdữ liệu. Kỹ thuật này hữu ích khi chúng ta có xác suất trong tập dữ liệu của mình và muốn chuyển chúng thành các giá trị rõ nét.
Chúng ta có thể mã hóa dữ liệu với sự trợ giúp của lớp Binarizer của thư viện Python scikit-learning.
Thí dụ
Trong ví dụ này, chúng tôi sẽ bán lại dữ liệu của bộ dữ liệu bệnh tiểu đường người da đỏ Pima mà chúng tôi đã sử dụng trước đó. Đầu tiên, dữ liệu CSV sẽ được tải và sau đó với sự trợ giúp của lớp Binarizer, nó sẽ được chuyển đổi thành các giá trị nhị phân, tức là 0 và 1 tùy thuộc vào giá trị ngưỡng. Chúng tôi đang lấy 0,5 làm giá trị ngưỡng.
Vài dòng đầu tiên của tập lệnh sau giống như chúng ta đã viết trong các chương trước khi tải dữ liệu CSV.
from pandas import read_csv
from sklearn.preprocessing import Binarizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesBây giờ, chúng ta có thể sử dụng lớp Binarize để chuyển đổi dữ liệu thành các giá trị nhị phân.
binarizer = Binarizer(threshold=0.5).fit(array)
Data_binarized = binarizer.transform(array)Ở đây, chúng tôi đang hiển thị 5 hàng đầu tiên trong đầu ra.
print ("\nBinary data:\n", Data_binarized [0:5])Đầu ra
Binary data:
[[1. 1. 1. 1. 0. 1. 1. 1. 1.]
[1. 1. 1. 1. 0. 1. 0. 1. 0.]
[1. 1. 1. 0. 0. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 0. 1. 0.]
[0. 1. 1. 1. 1. 1. 1. 1. 1.]]Tiêu chuẩn hóa
Một kỹ thuật tiền xử lý dữ liệu hữu ích khác về cơ bản được sử dụng để biến đổi các thuộc tính dữ liệu với phân phối Gaussian. Nó khác giá trị trung bình và SD (Độ lệch chuẩn) với phân phối Gaussian chuẩn với giá trị trung bình là 0 và SD là 1. Kỹ thuật này hữu ích trong các thuật toán ML như hồi quy tuyến tính, hồi quy logistic giả định phân phối Gaussian trong tập dữ liệu đầu vào và tạo ra tốt hơn kết quả với dữ liệu được thay đổi tỷ lệ. Chúng ta có thể chuẩn hóa dữ liệu (mean = 0 và SD = 1) với sự trợ giúp của lớp StandardScaler của thư viện Python scikit-learning.
Thí dụ
Trong ví dụ này, chúng tôi sẽ bán lại dữ liệu của bộ dữ liệu bệnh tiểu đường người da đỏ Pima mà chúng tôi đã sử dụng trước đó. Đầu tiên, dữ liệu CSV sẽ được tải và sau đó với sự trợ giúp của lớp StandardScaler, nó sẽ được chuyển đổi thành Phân phối Gaussian với giá trị trung bình = 0 và SD = 1.
Vài dòng đầu tiên của tập lệnh sau giống như chúng ta đã viết trong các chương trước khi tải dữ liệu CSV.
from sklearn.preprocessing import StandardScaler
from pandas import read_csv
from numpy import set_printoptions
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesBây giờ, chúng ta có thể sử dụng lớp StandardScaler để bán lại dữ liệu.
data_scaler = StandardScaler().fit(array)
data_rescaled = data_scaler.transform(array)Chúng tôi cũng có thể tóm tắt dữ liệu cho đầu ra theo lựa chọn của chúng tôi. Ở đây, chúng tôi đang đặt độ chính xác thành 2 và hiển thị 5 hàng đầu tiên trong đầu ra.
set_printoptions(precision=2)
print ("\nRescaled data:\n", data_rescaled [0:5])Đầu ra
Rescaled data:
[[ 0.64 0.85 0.15 0.91 -0.69 0.2 0.47 1.43 1.37]
[-0.84 -1.12 -0.16 0.53 -0.69 -0.68 -0.37 -0.19 -0.73]
[ 1.23 1.94 -0.26 -1.29 -0.69 -1.1 0.6 -0.11 1.37]
[-0.84 -1. -0.16 0.15 0.12 -0.49 -0.92 -1.04 -0.73]
[-1.14 0.5 -1.5 0.91 0.77 1.41 5.48 -0.02 1.37]]Ghi nhãn dữ liệu
Chúng tôi đã thảo luận về tầm quan trọng của fata tốt đối với các thuật toán ML cũng như một số kỹ thuật để xử lý trước dữ liệu trước khi gửi nó đến các thuật toán ML. Một khía cạnh nữa trong vấn đề này là ghi nhãn dữ liệu. Nó cũng rất quan trọng để gửi dữ liệu đến các thuật toán ML có nhãn thích hợp. Ví dụ, trong trường hợp các vấn đề phân loại, rất nhiều nhãn ở dạng từ, số, v.v. có trên dữ liệu.
Mã hóa nhãn là gì?
Hầu hết các hàm sklearn đều mong đợi rằng dữ liệu có nhãn số hơn là nhãn từ. Do đó, chúng ta cần chuyển đổi các nhãn đó thành nhãn số. Quá trình này được gọi là mã hóa nhãn. Chúng ta có thể thực hiện mã hóa nhãn của dữ liệu với sự trợ giúp của hàm LabelEncoder () của thư viện Python scikit-learning.
Thí dụ
Trong ví dụ sau, tập lệnh Python sẽ thực hiện mã hóa nhãn.
Đầu tiên, nhập các thư viện Python được yêu cầu như sau:
import numpy as np
from sklearn import preprocessingBây giờ, chúng ta cần cung cấp các nhãn đầu vào như sau:
input_labels = ['red','black','red','green','black','yellow','white']Dòng mã tiếp theo sẽ tạo bộ mã hóa nhãn và đào tạo nó.
encoder = preprocessing.LabelEncoder()
encoder.fit(input_labels)Các dòng tiếp theo của tập lệnh sẽ kiểm tra hiệu suất bằng cách mã hóa danh sách được sắp xếp ngẫu nhiên -
test_labels = ['green','red','black']
encoded_values = encoder.transform(test_labels)
print("\nLabels =", test_labels)
print("Encoded values =", list(encoded_values))
encoded_values = [3,0,4,1]
decoded_list = encoder.inverse_transform(encoded_values)Chúng tôi có thể lấy danh sách các giá trị được mã hóa với sự trợ giúp của tập lệnh python sau:
print("\nEncoded values =", encoded_values)
print("\nDecoded labels =", list(decoded_list))Đầu ra
Labels = ['green', 'red', 'black']
Encoded values = [1, 2, 0]
Encoded values = [3, 0, 4, 1]
Decoded labels = ['white', 'black', 'yellow', 'green']Trong chương trước, chúng ta đã xem chi tiết cách xử lý trước và chuẩn bị dữ liệu cho học máy. Trong chương này, chúng ta hãy hiểu chi tiết lựa chọn tính năng dữ liệu và các khía cạnh khác nhau liên quan đến nó.
Tầm quan trọng của việc lựa chọn tính năng dữ liệu
Hiệu suất của mô hình học máy tỷ lệ thuận với các tính năng dữ liệu được sử dụng để đào tạo nó. Hiệu suất của mô hình ML sẽ bị ảnh hưởng tiêu cực nếu các tính năng dữ liệu được cung cấp cho nó không liên quan. Mặt khác, việc sử dụng các tính năng dữ liệu có liên quan có thể làm tăng độ chính xác của mô hình ML của bạn, đặc biệt là hồi quy tuyến tính và logistic.
Bây giờ câu hỏi nảy sinh rằng lựa chọn tính năng tự động là gì? Nó có thể được định nghĩa là quá trình với sự trợ giúp của chúng tôi chọn các tính năng đó trong dữ liệu của chúng tôi có liên quan nhất đến biến đầu ra hoặc dự đoán mà chúng tôi quan tâm. Nó còn được gọi là lựa chọn thuộc tính.
Sau đây là một số lợi ích của việc lựa chọn tính năng tự động trước khi lập mô hình dữ liệu:
Thực hiện lựa chọn tính năng trước khi lập mô hình dữ liệu sẽ làm giảm sự trang bị quá mức.
Thực hiện lựa chọn tính năng trước khi lập mô hình dữ liệu sẽ làm tăng độ chính xác của mô hình ML.
Thực hiện lựa chọn tính năng trước khi lập mô hình dữ liệu sẽ giảm thời gian đào tạo
Kỹ thuật chọn tính năng
Sau đây là các kỹ thuật chọn tính năng tự động mà chúng ta có thể sử dụng để lập mô hình dữ liệu ML bằng Python:
Lựa chọn đơn biến
Kỹ thuật lựa chọn tính năng này rất hữu ích trong việc lựa chọn các tính năng đó, với sự trợ giúp của kiểm tra thống kê, có mối quan hệ chặt chẽ nhất với các biến dự đoán. Chúng ta có thể triển khai kỹ thuật lựa chọn tính năng đơn biến với sự trợ giúp của SelectKBest0class của thư viện Python scikit-learning.
Example
Trong ví dụ này, chúng tôi sẽ sử dụng tập dữ liệu bệnh tiểu đường của người da đỏ Pima để chọn 4 trong số các thuộc tính có các tính năng tốt nhất với sự trợ giúp của kiểm tra thống kê chi-bình phương.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesTiếp theo, chúng ta sẽ tách mảng thành các thành phần đầu vào và đầu ra -
X = array[:,0:8]
Y = array[:,8]Các dòng mã sau sẽ chọn các tính năng tốt nhất từ tập dữ liệu -
test = SelectKBest(score_func=chi2, k=4)
fit = test.fit(X,Y)Chúng tôi cũng có thể tóm tắt dữ liệu cho đầu ra theo lựa chọn của chúng tôi. Ở đây, chúng tôi đang đặt độ chính xác thành 2 và hiển thị 4 thuộc tính dữ liệu với các tính năng tốt nhất cùng với điểm tốt nhất của từng thuộc tính -
set_printoptions(precision=2)
print(fit.scores_)
featured_data = fit.transform(X)
print ("\nFeatured data:\n", featured_data[0:4])Output
[ 111.52 1411.89 17.61 53.11 2175.57 127.67 5.39 181.3 ]
Featured data:
[[148. 0. 33.6 50. ]
[ 85. 0. 26.6 31. ]
[183. 0. 23.3 32. ]
[ 89. 94. 28.1 21. ]]Loại bỏ tính năng đệ quy
Như tên cho thấy, kỹ thuật lựa chọn tính năng RFE (Loại bỏ tính năng đệ quy) loại bỏ các thuộc tính một cách đệ quy và xây dựng mô hình với các thuộc tính còn lại. Chúng ta có thể triển khai kỹ thuật lựa chọn tính năng RFE với sự trợ giúp của lớp RFE của thư viện Python scikit-learning.
Thí dụ
Trong ví dụ này, chúng tôi sẽ sử dụng RFE với thuật toán hồi quy logistic để chọn 3 thuộc tính tốt nhất có các tính năng tốt nhất từ tập dữ liệu Bệnh tiểu đường người da đỏ Pima.
from pandas import read_csv
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesTiếp theo, chúng ta sẽ tách mảng thành các thành phần đầu vào và đầu ra của nó -
X = array[:,0:8]
Y = array[:,8]Các dòng mã sau sẽ chọn các tính năng tốt nhất từ tập dữ liệu -
model = LogisticRegression()
rfe = RFE(model, 3)
fit = rfe.fit(X, Y)
print("Number of Features: %d")
print("Selected Features: %s")
print("Feature Ranking: %s")Đầu ra
Number of Features: 3
Selected Features: [ True False False False False True True False]
Feature Ranking: [1 2 3 5 6 1 1 4]Chúng ta có thể thấy ở đầu ra trên, RFE chọn preg, mass và pedi là 3 tính năng tốt nhất đầu tiên. Chúng được đánh dấu là 1 trong đầu ra.
Phân tích thành phần chính (PCA)
PCA, thường được gọi là kỹ thuật giảm dữ liệu, là kỹ thuật lựa chọn tính năng rất hữu ích vì nó sử dụng đại số tuyến tính để biến đổi tập dữ liệu thành dạng nén. Chúng ta có thể triển khai kỹ thuật lựa chọn tính năng PCA với sự trợ giúp của lớp PCA của thư viện Python scikit-learning. Chúng ta có thể chọn số lượng các thành phần chính trong đầu ra.
Thí dụ
Trong ví dụ này, chúng tôi sẽ sử dụng PCA để chọn 3 thành phần chính tốt nhất từ bộ dữ liệu bệnh tiểu đường của người da đỏ Pima.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesTiếp theo, chúng ta sẽ tách mảng thành các thành phần đầu vào và đầu ra -
X = array[:,0:8]
Y = array[:,8]Các dòng mã sau sẽ trích xuất các tính năng từ tập dữ liệu:
pca = PCA(n_components=3)
fit = pca.fit(X)
print("Explained Variance: %s") % fit.explained_variance_ratio_
print(fit.components_)Đầu ra
Explained Variance: [ 0.88854663 0.06159078 0.02579012]
[[ -2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-02
9.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[ 2.26488861e-02 9.72210040e-01 1.41909330e-01 -5.78614699e-02
-9.46266913e-02 4.69729766e-02 8.16804621e-04 1.40168181e-01]
[ -2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-01
2.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]]Chúng ta có thể quan sát từ đầu ra ở trên rằng 3 Thành phần chính có chút tương đồng với dữ liệu nguồn.
Tầm quan trọng của tính năng
Như tên cho thấy, kỹ thuật mức độ quan trọng của đối tượng địa lý được sử dụng để chọn các tính năng quan trọng. Về cơ bản, nó sử dụng một bộ phân loại có giám sát được đào tạo để chọn các tính năng. Chúng ta có thể thực hiện kỹ thuật lựa chọn tính năng này với sự trợ giúp của lớp ExtraTreeClassifier của thư viện Python scikit-learning.
Thí dụ
Trong ví dụ này, chúng tôi sẽ sử dụng ExtraTreeClassifier để chọn các tính năng từ bộ dữ liệu bệnh tiểu đường của người da đỏ Pima.
from pandas import read_csv
from sklearn.ensemble import ExtraTreesClassifier
path = r'C:\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(data, names=names)
array = dataframe.valuesTiếp theo, chúng ta sẽ tách mảng thành các thành phần đầu vào và đầu ra -
X = array[:,0:8]
Y = array[:,8]Các dòng mã sau sẽ trích xuất các tính năng từ tập dữ liệu:
model = ExtraTreesClassifier()
model.fit(X, Y)
print(model.feature_importances_)Đầu ra
[ 0.11070069 0.2213717 0.08824115 0.08068703 0.07281761 0.14548537 0.12654214 0.15415431]Từ kết quả đầu ra, chúng ta có thể quan sát rằng có điểm cho mỗi thuộc tính. Điểm càng cao thì mức độ quan trọng của thuộc tính đó càng cao.
Giới thiệu về phân loại
Phân loại có thể được định nghĩa là quá trình dự đoán lớp hoặc loại từ các giá trị quan sát hoặc các điểm dữ liệu đã cho. Đầu ra được phân loại có thể có dạng như “Đen” hoặc “Trắng” hoặc “thư rác” hoặc “không có thư rác”.
Về mặt toán học, phân loại là nhiệm vụ xấp xỉ một hàm ánh xạ (f) từ biến đầu vào (X) đến biến đầu ra (Y). Về cơ bản, nó thuộc về học máy có giám sát, trong đó các mục tiêu cũng được cung cấp cùng với tập dữ liệu đầu vào.
Một ví dụ về vấn đề phân loại có thể là phát hiện thư rác trong email. Chỉ có thể có hai loại đầu ra, "thư rác" và "không có thư rác"; do đó đây là phân loại kiểu nhị phân.
Để thực hiện phân loại này, trước tiên chúng ta cần đào tạo trình phân loại. Đối với ví dụ này, email "spam" và "không spam" sẽ được sử dụng làm dữ liệu đào tạo. Sau khi huấn luyện thành công bộ phân loại, nó có thể được sử dụng để phát hiện một email không xác định.
Các loại người học trong phân loại
Chúng tôi có hai loại người học tương ứng với các vấn đề phân loại -
Người học lười biếng
Như tên gọi cho thấy, những người học như vậy sẽ đợi dữ liệu kiểm tra xuất hiện sau khi lưu trữ dữ liệu đào tạo. Việc phân loại chỉ được thực hiện sau khi nhận được dữ liệu thử nghiệm. Họ dành ít thời gian hơn cho việc đào tạo nhưng nhiều thời gian hơn cho việc dự đoán. Ví dụ về những người lười học là K-láng giềng gần nhất và suy luận dựa trên tình huống.
Người học háo hức
Ngược lại với những người lười học, những người ham học hỏi xây dựng mô hình phân loại mà không cần đợi dữ liệu kiểm tra xuất hiện sau khi lưu trữ dữ liệu đào tạo. Họ dành nhiều thời gian hơn cho việc đào tạo nhưng ít thời gian hơn cho việc dự đoán. Các ví dụ về những người ham học hỏi là Cây quyết định, Vịnh Naïve và Mạng thần kinh nhân tạo (ANN).
Xây dựng bộ phân loại bằng Python
Scikit-learning, một thư viện Python dành cho học máy có thể được sử dụng để xây dựng bộ phân loại bằng Python. Các bước để xây dựng một trình phân loại trong Python như sau:
Bước 1: Nhập gói python cần thiết
Để xây dựng bộ phân loại bằng scikit-learning, chúng ta cần nhập nó. Chúng tôi có thể nhập nó bằng cách sử dụng tập lệnh sau:
import sklearnBước 2: Nhập tập dữ liệu
Sau khi nhập gói cần thiết, chúng ta cần một tập dữ liệu để xây dựng mô hình dự đoán phân loại. Chúng tôi có thể nhập nó từ tập dữ liệu sklearn hoặc có thể sử dụng tập dữ liệu khác theo yêu cầu của chúng tôi. Chúng tôi sẽ sử dụng Cơ sở dữ liệu chẩn đoán ung thư vú Wisconsin của sklearn. Chúng tôi có thể nhập nó với sự trợ giúp của tập lệnh sau:
from sklearn.datasets import load_breast_cancerTập lệnh sau sẽ tải tập dữ liệu;
data = load_breast_cancer()Chúng tôi cũng cần tổ chức dữ liệu và nó có thể được thực hiện với sự trợ giúp của các tập lệnh sau:
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']Lệnh sau sẽ in tên nhãn, 'ác tính' và 'lành tính' trong trường hợp cơ sở dữ liệu của chúng tôi.
print(label_names)Đầu ra của lệnh trên là tên của các nhãn -
['malignant' 'benign']Các nhãn này được ánh xạ tới các giá trị nhị phân 0 và 1. Malignant ung thư được biểu thị bằng 0 và Benign ung thư được đại diện bởi 1.
Tên đặc điểm và giá trị đặc điểm của các nhãn này có thể được nhìn thấy với sự trợ giúp của các lệnh sau:
print(feature_names[0])Đầu ra của lệnh trên là tên của các tính năng cho nhãn 0 tức là Malignant ung thư -
mean radiusTương tự, tên của các tính năng cho nhãn có thể được tạo ra như sau:
print(feature_names[1])Đầu ra của lệnh trên là tên của các tính năng cho nhãn 1 tức là Benign ung thư -
mean textureChúng ta có thể in các tính năng cho các nhãn này với sự trợ giúp của lệnh sau:
print(features[0])Điều này sẽ cho kết quả sau:
[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
4.601e-01 1.189e-01]Chúng ta có thể in các tính năng cho các nhãn này với sự trợ giúp của lệnh sau:
print(features[1])Điều này sẽ cho kết quả sau:
[2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
2.750e-01 8.902e-02]Bước 3: Tổ chức dữ liệu thành các bộ đào tạo và kiểm tra
Khi chúng tôi cần kiểm tra mô hình của mình trên dữ liệu không nhìn thấy, chúng tôi sẽ chia tập dữ liệu của mình thành hai phần: tập huấn luyện và tập thử nghiệm. Chúng ta có thể sử dụng hàm train_test_split () của gói python sklearn để chia dữ liệu thành các bộ. Lệnh sau sẽ nhập hàm:
from sklearn.model_selection import train_test_splitBây giờ, lệnh tiếp theo sẽ chia dữ liệu thành dữ liệu đào tạo và kiểm tra. Trong ví dụ này, chúng tôi đang sử dụng việc lấy 40% dữ liệu cho mục đích thử nghiệm và 60% dữ liệu cho mục đích đào tạo -
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)Bước 4 - Đánh giá mô hình
Sau khi phân chia dữ liệu thành đào tạo và thử nghiệm, chúng ta cần xây dựng mô hình. Chúng tôi sẽ sử dụng thuật toán Naïve Bayes cho mục đích này. Các lệnh sau sẽ nhập mô-đun GaussianNB:
from sklearn.naive_bayes import GaussianNBBây giờ, khởi tạo mô hình như sau:
gnb = GaussianNB()Tiếp theo, với sự trợ giúp của lệnh sau, chúng ta có thể huấn luyện mô hình:
model = gnb.fit(train, train_labels)Bây giờ, cho mục đích đánh giá, chúng tôi cần đưa ra dự đoán. Nó có thể được thực hiện bằng cách sử dụng hàm dự đoán () như sau:
preds = gnb.predict(test)
print(preds)Điều này sẽ cho kết quả sau:
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0
1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0
1 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0
1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0
1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0
0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1
0 0 1 1 0 1]Chuỗi số 0 và 1 ở trên ở đầu ra là các giá trị dự đoán cho Malignant và Benign các lớp khối u.
Bước 5- Tìm độ chính xác
Chúng ta có thể tìm thấy độ chính xác của việc xây dựng mô hình ở bước trước bằng cách so sánh hai mảng là test_labels và preds. Chúng tôi sẽ sử dụng hàm precision_score () để xác định độ chính xác.
from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965Kết quả trên cho thấy trình phân loại NaïveBayes chính xác 95,17%.
Số liệu đánh giá phân loại
Công việc vẫn chưa hoàn thành ngay cả khi bạn đã hoàn thành việc triển khai ứng dụng hoặc mô hình Máy học của mình. Chúng ta phải tìm hiểu xem mô hình của mình có hiệu quả không? Có thể có các số liệu đánh giá khác nhau, nhưng chúng ta phải lựa chọn cẩn thận vì việc lựa chọn số liệu ảnh hưởng đến cách đo lường và so sánh hiệu suất của thuật toán học máy.
Sau đây là một số chỉ số đánh giá phân loại quan trọng mà bạn có thể chọn dựa trên tập dữ liệu và loại vấn đề của mình -
Ma trận hỗn loạn
Đây là cách dễ nhất để đo lường hiệu suất của một bài toán phân loại trong đó kết quả đầu ra có thể là hai hoặc nhiều loại lớp. Ma trận nhầm lẫn không là gì ngoài một bảng có hai chiều viz. “Thực tế” và “Dự đoán” và hơn nữa, cả hai thứ nguyên đều có “Khẳng định thật (TP)”, “Phủ định thật (TN)”, “Khẳng định sai (FP)”, “Phủ định giả (FN)” như được hiển thị bên dưới -

True Positives (TP) - Đó là trường hợp khi cả lớp thực tế và lớp dự đoán của điểm dữ liệu là 1.
True Negatives (TN) - Đó là trường hợp khi cả lớp thực tế và lớp dự đoán của điểm dữ liệu là 0.
False Positives (FP) - Trường hợp lớp điểm dữ liệu thực tế là 0 và lớp điểm dữ liệu dự đoán là 1.
False Negatives (FN) - Trường hợp lớp điểm dữ liệu thực tế là 1 & lớp điểm dữ liệu dự đoán là 0.
Chúng ta có thể tìm thấy ma trận nhầm lẫn với sự trợ giúp của hàm mess_matrix () của sklearn. Với sự trợ giúp của tập lệnh sau, chúng ta có thể tìm thấy ma trận nhầm lẫn của bộ phân loại nhị phân được xây dựng ở trên:
from sklearn.metrics import confusion_matrixĐầu ra
[[ 73 7]
[ 4 144]]Sự chính xác
Nó có thể được định nghĩa là số dự đoán đúng được thực hiện bởi mô hình ML của chúng tôi. Chúng ta có thể dễ dàng tính toán nó bằng ma trận nhầm lẫn với sự trợ giúp của công thức sau:
$$=\frac{+}{+++}$$Đối với bộ phân loại nhị phân đã xây dựng ở trên, TP + TN = 73 + 144 = 217 và TP + FP + FN + TN = 73 + 7 + 4 + 144 = 228.
Do đó, Độ chính xác = 217/288 = 0,951754385965, giống như chúng tôi đã tính sau khi tạo bộ phân loại nhị phân.
Độ chính xác
Độ chính xác, được sử dụng trong truy xuất tài liệu, có thể được định nghĩa là số lượng tài liệu chính xác được trả về bởi mô hình ML của chúng tôi. Chúng ta có thể dễ dàng tính toán nó bằng ma trận nhầm lẫn với sự trợ giúp của công thức sau:
$$=\frac{}{+FP}$$Đối với bộ phân loại nhị phân được xây dựng ở trên, TP = 73 và TP + FP = 73 + 7 = 80.
Do đó, Độ chính xác = 73/80 = 0,915
Nhớ lại hoặc độ nhạy
Thu hồi có thể được định nghĩa là số lượng dương tính được trả về bởi mô hình ML của chúng tôi. Chúng ta có thể dễ dàng tính toán nó bằng ma trận nhầm lẫn với sự trợ giúp của công thức sau:
$$=\frac{}{+FN}$$Đối với bộ phân loại nhị phân được xây dựng ở trên, TP = 73 và TP + FN = 73 + 4 = 77.
Do đó, Độ chính xác = 73/77 = 0,94805
Tính đặc hiệu
Tính cụ thể, trái ngược với thu hồi, có thể được định nghĩa là số lượng các phủ định được trả về bởi mô hình ML của chúng tôi. Chúng ta có thể dễ dàng tính toán nó bằng ma trận nhầm lẫn với sự trợ giúp của công thức sau:
$$=\frac{N}{N+FP}$$Đối với bộ phân loại nhị phân được xây dựng ở trên, TN = 144 và TN + FP = 144 + 7 = 151.
Do đó, Độ chính xác = 144/151 = 0,95364
Các thuật toán phân loại ML khác nhau
Sau đây là một số thuật toán phân loại ML quan trọng:
Hồi quy logistic
Máy vectơ hỗ trợ (SVM)
Cây quyết định
Naïve Bayes
Rừng ngẫu nhiên
Chúng ta sẽ thảo luận chi tiết về tất cả các thuật toán phân loại này trong các chương tiếp theo.
Các ứng dụng
Một số ứng dụng quan trọng nhất của thuật toán phân loại như sau:
Nhận dạng giọng nói
Nhận dang chu Viet
Nhận dạng sinh trắc học
Phân loại tài liệu
Giới thiệu về hồi quy logistic
Hồi quy logistic là một thuật toán phân loại học có giám sát được sử dụng để dự đoán xác suất của một biến mục tiêu. Bản chất của biến đích hoặc biến phụ thuộc là phân đôi, có nghĩa là chỉ có thể có hai lớp.
Nói một cách đơn giản, biến phụ thuộc có bản chất là nhị phân có dữ liệu được mã hóa là 1 (viết tắt của thành công / có) hoặc 0 (viết tắt của thất bại / không).
Về mặt toán học, mô hình hồi quy logistic dự đoán P (Y = 1) là một hàm của X. Đây là một trong những thuật toán ML đơn giản nhất có thể được sử dụng cho các vấn đề phân loại khác nhau như phát hiện thư rác, dự đoán bệnh tiểu đường, phát hiện ung thư, v.v.
Các loại hồi quy logistic
Nói chung, hồi quy logistic có nghĩa là hồi quy logistic nhị phân có các biến mục tiêu nhị phân, nhưng có thể có thêm hai loại biến mục tiêu có thể được dự đoán bởi nó. Dựa trên số lượng các loại đó, hồi quy Logistic có thể được chia thành các loại sau:
Nhị phân hoặc nhị thức
Theo kiểu phân loại như vậy, một biến phụ thuộc sẽ chỉ có hai kiểu khả dĩ là 1 và 0. Ví dụ, những biến này có thể đại diện cho thành công hoặc thất bại, có hoặc không, thắng hoặc thua, v.v.
Đa thức
Trong kiểu phân loại như vậy, biến phụ thuộc có thể có 3 hoặc nhiều kiểu không có thứ tự hoặc các kiểu không có ý nghĩa định lượng. Ví dụ: các biến này có thể đại diện cho “Loại A” hoặc “Loại B” hoặc “Loại C”.
Bình thường
Trong kiểu phân loại như vậy, biến phụ thuộc có thể có 3 kiểu có thứ tự trở lên hoặc kiểu có ý nghĩa định lượng. Ví dụ: các biến này có thể đại diện cho “kém” hoặc “tốt”, “rất tốt”, “Xuất sắc” và mỗi loại có thể có các điểm như 0,1,2,3.
Các giả định hồi quy logistic
Trước khi đi sâu vào việc triển khai hồi quy logistic, chúng ta phải biết các giả định sau về cùng một:
Trong trường hợp hồi quy logistic nhị phân, các biến mục tiêu phải luôn luôn là nhị phân và kết quả mong muốn được biểu thị bằng cấp nhân tố 1.
Không nên có bất kỳ đa cộng tuyến nào trong mô hình, có nghĩa là các biến độc lập phải độc lập với nhau.
Chúng ta phải đưa các biến có ý nghĩa vào mô hình của mình.
Chúng ta nên chọn kích thước mẫu lớn cho hồi quy logistic.
Mô hình hồi quy logistic nhị phân
Hình thức đơn giản nhất của hồi quy logistic là hồi quy logistic nhị phân hoặc nhị thức trong đó biến mục tiêu hoặc biến phụ thuộc chỉ có thể có 2 loại có thể là 1 hoặc 0. Nó cho phép chúng ta lập mô hình mối quan hệ giữa nhiều biến dự báo và biến mục tiêu nhị phân / nhị thức. Trong trường hợp hồi quy logistic, hàm tuyến tính về cơ bản được sử dụng làm đầu vào cho một hàm khác, chẳng hạn như trong quan hệ sau:
$h_{\theta}{(x)}=g(\theta^{T}x)ℎ 0≤h_{\theta}≤1$Đây là hàm logistic hoặc hàm sigmoid có thể được đưa ra như sau:
$g(z)= \frac{1}{1+e^{-z}}ℎ =\theta ^{T}$Đường cong sigmoid có thể được biểu diễn với sự trợ giúp của đồ thị sau. Chúng ta có thể thấy các giá trị của trục y nằm giữa 0 và 1 và cắt trục tại 0,5.

Các lớp có thể được chia thành tích cực hoặc tiêu cực. Đầu ra theo xác suất của lớp dương nếu nó nằm trong khoảng từ 0 đến 1. Đối với việc triển khai của chúng tôi, chúng tôi đang giải thích đầu ra của hàm giả thuyết là dương nếu nó ≥0,5, ngược lại là âm.
Chúng ta cũng cần xác định một hàm mất mát để đo lường mức độ hoạt động của thuật toán bằng cách sử dụng các trọng số trên các hàm, được biểu diễn bằng theta như sau:
ℎ = ()
$J(\theta) = \frac{1}{m}.(-y^{T}log(h) - (1 -y)^Tlog(1-h))$Bây giờ, sau khi xác định hàm mất mát, mục tiêu chính của chúng ta là giảm thiểu hàm mất mát. Nó có thể được thực hiện với sự trợ giúp của việc lắp các quả nặng có nghĩa là tăng hoặc giảm khối lượng. Với sự trợ giúp của các dẫn xuất của hàm giảm theo từng trọng lượng, chúng ta sẽ có thể biết thông số nào nên có trọng lượng cao và thông số nào nên có trọng lượng nhỏ hơn.
Phương trình giảm độ dốc sau đây cho chúng ta biết tổn thất sẽ thay đổi như thế nào nếu chúng ta sửa đổi các thông số:
$\frac{()}{\theta_{j}}=\frac{1}{m}X^{T}(()−)$Triển khai bằng Python
Bây giờ chúng ta sẽ triển khai khái niệm ở trên về hồi quy logistic nhị thức trong Python. Với mục đích này, chúng tôi đang sử dụng tập dữ liệu hoa đa biến có tên 'iris', có 3 lớp, mỗi lớp 50 trường hợp, nhưng chúng tôi sẽ sử dụng hai cột tính năng đầu tiên. Mỗi lớp đại diện cho một loại hoa diên vĩ.
Đầu tiên, chúng ta cần nhập các thư viện cần thiết như sau:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasetsTiếp theo, tải tập dữ liệu mống mắt như sau:
iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1Chúng ta có thể vẽ biểu đồ dữ liệu đào tạo của mình như sau:
plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();
Tiếp theo, chúng ta sẽ xác định hàm sigmoid, hàm mất mát và giảm dần gradient như sau:
class LogisticRegression:
def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
self.lr = lr
self.num_iter = num_iter
self.fit_intercept = fit_intercept
self.verbose = verbose
def __add_intercept(self, X):
intercept = np.ones((X.shape[0], 1))
return np.concatenate((intercept, X), axis=1)
def __sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def __loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def fit(self, X, y):
if self.fit_intercept:
X = self.__add_intercept(X)Bây giờ, khởi tạo các trọng số như sau:
self.theta = np.zeros(X.shape[1])
for i in range(self.num_iter):
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
gradient = np.dot(X.T, (h - y)) / y.size
self.theta -= self.lr * gradient
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
loss = self.__loss(h, y)
if(self.verbose ==True and i % 10000 == 0):
print(f'loss: {loss} \t')Với sự trợ giúp của tập lệnh sau, chúng ta có thể dự đoán các xác suất đầu ra -
def predict_prob(self, X):
if self.fit_intercept:
X = self.__add_intercept(X)
return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
return self.predict_prob(X).round()Tiếp theo, chúng ta có thể đánh giá mô hình và vẽ biểu đồ như sau:
model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()
plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');
Mô hình hồi quy logistic đa thức
Một dạng hồi quy logistic hữu ích khác là hồi quy logistic đa thức trong đó biến mục tiêu hoặc biến phụ thuộc có thể có 3 hoặc nhiều hơn các kiểu không có thứ tự, tức là các kiểu không có ý nghĩa định lượng.
Triển khai bằng Python
Bây giờ chúng ta sẽ triển khai khái niệm hồi quy logistic đa thức ở trên trong Python. Vì mục đích này, chúng tôi đang sử dụng tập dữ liệu từ chữ số có tên sklearn.
Đầu tiên, chúng ta cần nhập các thư viện cần thiết như sau:
Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_splitTiếp theo, chúng ta cần tải tập dữ liệu chữ số -
digits = datasets.load_digits()Bây giờ, hãy xác định ma trận đặc trưng (X) và vectơ phản hồi (y) như sau:
X = digits.data
y = digits.targetVới sự trợ giúp của dòng mã tiếp theo, chúng ta có thể chia X và y thành các tập huấn luyện và thử nghiệm -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)Bây giờ hãy tạo một đối tượng của hồi quy logistic như sau:
digreg = linear_model.LogisticRegression()Bây giờ, chúng ta cần huấn luyện mô hình bằng cách sử dụng các tập huấn luyện như sau:
digreg.fit(X_train, y_train)Tiếp theo, thực hiện các dự đoán về bộ thử nghiệm như sau:
y_pred = digreg.predict(X_test)Tiếp theo in độ chính xác của mô hình như sau:
print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)Đầu ra
Accuracy of Logistic Regression model is: 95.6884561891516Từ kết quả trên, chúng ta có thể thấy độ chính xác của mô hình của chúng tôi là khoảng 96%.
Giới thiệu về SVM
Máy vectơ hỗ trợ (SVM) là các thuật toán học máy được giám sát mạnh mẽ nhưng linh hoạt được sử dụng cho cả phân loại và hồi quy. Nhưng nhìn chung, chúng được sử dụng trong các bài toán phân loại. Năm 1960, SVM lần đầu tiên được giới thiệu nhưng sau đó chúng được cải tiến vào năm 1990. SVM có cách triển khai độc đáo so với các thuật toán học máy khác. Gần đây, chúng cực kỳ phổ biến vì khả năng xử lý nhiều biến liên tục và phân loại.
Hoạt động của SVM
Mô hình SVM về cơ bản là sự biểu diễn của các lớp khác nhau trong một siêu phẳng trong không gian đa chiều. Siêu phẳng sẽ được SVM tạo theo cách lặp đi lặp lại để có thể giảm thiểu lỗi. Mục tiêu của SVM là chia bộ dữ liệu thành các lớp để tìm siêu phẳng biên tối đa (MMH).

Sau đây là các khái niệm quan trọng trong SVM:
Support Vectors- Các điểm dữ liệu gần siêu phẳng nhất được gọi là vectơ hỗ trợ. Đường phân cách sẽ được xác định với sự trợ giúp của các điểm dữ liệu này.
Hyperplane - Như chúng ta thấy trong sơ đồ trên, nó là một mặt phẳng quyết định hoặc không gian được phân chia giữa một tập các đối tượng có các lớp khác nhau.
Margin- Nó có thể được định nghĩa là khoảng cách giữa hai dòng trên các điểm dữ liệu tủ quần áo của các lớp khác nhau. Nó có thể được tính bằng khoảng cách vuông góc từ đường thẳng đến các vectơ hỗ trợ. Ký quỹ lớn được coi là ký quỹ tốt và ký quỹ nhỏ được coi là ký quỹ xấu.
Mục tiêu chính của SVM là chia bộ dữ liệu thành các lớp để tìm siêu phẳng biên tối đa (MMH) và nó có thể được thực hiện theo hai bước sau:
Đầu tiên, SVM sẽ tạo lặp đi lặp lại các siêu máy bay để phân tách các lớp theo cách tốt nhất.
Sau đó, nó sẽ chọn siêu phẳng phân tách các lớp một cách chính xác.
Triển khai SVM bằng Python
Để triển khai SVM bằng Python, chúng ta sẽ bắt đầu với việc nhập các thư viện tiêu chuẩn như sau:
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns; sns.set()Tiếp theo, chúng tôi đang tạo một tập dữ liệu mẫu, có dữ liệu có thể phân tách tuyến tính, từ sklearn.dataset.sample_generator để phân loại bằng SVM -
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=0.50)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');Sau đây là kết quả đầu ra sau khi tạo tập dữ liệu mẫu có 100 mẫu và 2 cụm -

Chúng tôi biết rằng SVM hỗ trợ phân loại phân biệt. nó phân chia các lớp với nhau bằng cách đơn giản tìm một đoạn thẳng trong trường hợp hai chiều hoặc đa tạp trong trường hợp nhiều chiều. Nó được thực hiện trên tập dữ liệu trên như sau:
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
plt.plot([0.6], [2.1], 'x', color='black', markeredgewidth=4, markersize=12)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);Kết quả như sau:

Chúng ta có thể thấy từ kết quả trên rằng có ba dải phân cách khác nhau phân biệt hoàn hảo các mẫu trên.
Như đã thảo luận, mục tiêu chính của SVM là chia bộ dữ liệu thành các lớp để tìm ra siêu phẳng biên tối đa (MMH), do đó thay vì vẽ một đường 0 giữa các lớp, chúng ta có thể vẽ xung quanh mỗi dòng một lề có độ rộng cho đến điểm gần nhất. Nó có thể được thực hiện như sau:
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
Từ hình ảnh trên trong đầu ra, chúng ta có thể dễ dàng quan sát “lề” trong các bộ phân loại phân biệt. SVM sẽ chọn dòng tối đa hóa lợi nhuận.
Tiếp theo, chúng tôi sẽ sử dụng bộ phân loại vector hỗ trợ của Scikit-Learn để đào tạo mô hình SVM trên dữ liệu này. Ở đây, chúng tôi đang sử dụng hạt nhân tuyến tính để phù hợp với SVM như sau:
from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear', C=1E10)
model.fit(X, y)Kết quả như sau:
SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)Bây giờ, để hiểu rõ hơn, phần sau sẽ vẽ sơ đồ các hàm quyết định cho 2D SVC:
def decision_function(model, ax=None, plot_support=True):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()Để đánh giá mô hình, chúng ta cần tạo lưới như sau:
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)Tiếp theo, chúng ta cần vẽ các ranh giới và biên quyết định như sau:
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])Bây giờ, vẽ biểu đồ tương tự các vectơ hỗ trợ như sau:
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)Bây giờ, sử dụng chức năng này để phù hợp với các mô hình của chúng tôi như sau:
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
decision_function(model);
Chúng ta có thể quan sát từ kết quả đầu ra ở trên rằng bộ phân loại SVM phù hợp với dữ liệu có lề tức là các đường đứt nét và các vectơ hỗ trợ, các phần tử quan trọng của sự phù hợp này, chạm vào đường đứt nét. Các điểm vectơ hỗ trợ này được lưu trữ trong thuộc tính support_vectors_ của trình phân loại như sau:
model.support_vectors_Kết quả như sau:
array([[0.5323772 , 3.31338909],
[2.11114739, 3.57660449],
[1.46870582, 1.86947425]])Nhân SVM
Trong thực tế, thuật toán SVM được thực hiện với hạt nhân để biến đổi không gian dữ liệu đầu vào thành dạng yêu cầu. SVM sử dụng một kỹ thuật gọi là kernel trick, trong đó kernel lấy một không gian đầu vào có chiều thấp và biến nó thành một không gian có chiều cao hơn. Nói một cách đơn giản, kernel chuyển đổi các vấn đề không thể phân tách thành các vấn đề có thể tách biệt bằng cách thêm nhiều chiều vào nó. Nó làm cho SVM mạnh mẽ, linh hoạt và chính xác hơn. Sau đây là một số loại hạt nhân được SVM sử dụng:
Kernel tuyến tính
Nó có thể được sử dụng như một sản phẩm chấm giữa hai lần quan sát bất kỳ. Công thức của hạt nhân tuyến tính như sau:
k (x, x i ) = sum (x * x i )
Từ công thức trên, chúng ta có thể thấy rằng tích giữa hai vectơ nói & là tổng của phép nhân của mỗi cặp giá trị đầu vào.
Nhân đa thức
Nó là dạng tổng quát hơn của nhân tuyến tính và phân biệt không gian đầu vào cong hoặc phi tuyến. Sau đây là công thức cho nhân đa thức:
K (x, xi) = 1 + sum (x * xi) ^ d
Ở đây d là bậc của đa thức mà chúng ta cần chỉ định thủ công trong thuật toán học.
Hạt nhân hàm cơ sở hướng tâm (RBF)
Nhân RBF, chủ yếu được sử dụng trong phân loại SVM, ánh xạ không gian đầu vào trong không gian chiều không xác định. Công thức sau giải thích nó về mặt toán học:
K (x, xi) = exp (-gamma * sum ((x - xi ^ 2))
Ở đây, gamma nằm trong khoảng từ 0 đến 1. Chúng ta cần chỉ định thủ công nó trong thuật toán học tập. Giá trị mặc định tốt của gamma là 0,1.
Khi chúng tôi triển khai SVM cho dữ liệu có thể phân tách tuyến tính, chúng tôi có thể triển khai nó bằng Python cho dữ liệu không thể phân tách tuyến tính. Nó có thể được thực hiện bằng cách sử dụng hạt nhân.
Thí dụ
Sau đây là một ví dụ để tạo bộ phân loại SVM bằng cách sử dụng hạt nhân. Chúng tôi sẽ sử dụng tập dữ liệu mống mắt từ scikit-learning -
Chúng tôi sẽ bắt đầu bằng cách nhập các gói sau:
import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as pltBây giờ, chúng ta cần tải dữ liệu đầu vào -
iris = datasets.load_iris()Từ tập dữ liệu này, chúng tôi sẽ sử dụng hai tính năng đầu tiên như sau:
X = iris.data[:, :2]
y = iris.targetTiếp theo, chúng tôi sẽ vẽ ranh giới SVM với dữ liệu gốc như sau:
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]Bây giờ, chúng ta cần cung cấp giá trị của tham số chính quy như sau:
C = 1.0Tiếp theo, đối tượng phân loại SVM có thể được tạo như sau:
Svc_classifier = svm.SVC (kernel = 'linear', C = C) .fit (X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with linear kernel')Đầu ra
Text(0.5, 1.0, 'Support Vector Classifier with linear kernel')
Để tạo bộ phân loại SVM với rbf kernel, chúng ta có thể thay đổi kernel thành rbf như sau -
Svc_classifier = svm.SVC(kernel='rbf', gamma =‘auto’,C=C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with rbf kernel')Đầu ra
Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel')
Chúng tôi đặt giá trị của gamma thành 'auto' nhưng bạn cũng có thể cung cấp giá trị của nó từ 0 đến 1.
Ưu và nhược điểm của Bộ phân loại SVM
Ưu điểm của bộ phân loại SVM
Bộ phân loại SVM cung cấp độ chính xác cao và hoạt động tốt với không gian chiều cao. Các bộ phân loại SVM về cơ bản sử dụng một tập hợp con các điểm đào tạo do đó sử dụng rất ít bộ nhớ.
Nhược điểm của bộ phân loại SVM
Chúng có thời gian đào tạo cao do đó trong thực tế không phù hợp với các bộ dữ liệu lớn. Một nhược điểm khác là bộ phân loại SVM không hoạt động tốt với các lớp chồng chéo.
Giới thiệu về cây quyết định
Nhìn chung, phân tích cây quyết định là một công cụ mô hình dự báo có thể được áp dụng trên nhiều lĩnh vực. Cây quyết định có thể được xây dựng bằng cách tiếp cận thuật toán có thể phân chia tập dữ liệu theo nhiều cách khác nhau dựa trên các điều kiện khác nhau. Quyết định tress là thuật toán mạnh nhất thuộc loại thuật toán được giám sát.
Chúng có thể được sử dụng cho cả nhiệm vụ phân loại và hồi quy. Hai thực thể chính của cây là các nút quyết định, nơi dữ liệu được phân chia và rời đi, nơi chúng ta có kết quả. Ví dụ về cây nhị phân để dự đoán một người phù hợp hay không phù hợp, cung cấp nhiều thông tin khác nhau như tuổi tác, thói quen ăn uống và thói quen tập thể dục, được đưa ra dưới đây:
Trong cây quyết định ở trên, câu hỏi là các nút quyết định và kết quả cuối cùng là các lá. Chúng ta có hai loại cây quyết định sau:
Classification decision trees- Trong loại cây quyết định này, biến quyết định là phân loại. Cây quyết định ở trên là một ví dụ về cây quyết định phân loại.
Regression decision trees - Trong loại cây quyết định này, biến quyết định là liên tục.
Triển khai thuật toán cây quyết định
Chỉ số Gini
Đây là tên của hàm chi phí được sử dụng để đánh giá các phân tách nhị phân trong tập dữ liệu và hoạt động với biến mục tiêu phân loại là “Thành công” hoặc “Thất bại”.
Giá trị của chỉ số Gini càng cao thì độ đồng nhất càng cao. Giá trị chỉ số Gini hoàn hảo là 0 và tệ nhất là 0,5 (đối với bài toán 2 lớp). Chỉ số Gini cho một phân tách có thể được tính toán với sự trợ giúp của các bước sau:
Đầu tiên, tính toán chỉ số Gini cho các nút con bằng công thức p ^ 2 + q ^ 2, là tổng bình phương của xác suất thành công và thất bại.
Tiếp theo, tính toán chỉ số Gini cho phần tách bằng cách sử dụng điểm Gini có trọng số của mỗi nút của phần tách đó.
Thuật toán Cây phân loại và hồi quy (CART) sử dụng phương pháp Gini để tạo ra các phân tách nhị phân.
Tạo tách
Phân tách về cơ bản bao gồm một thuộc tính trong tập dữ liệu và một giá trị. Chúng ta có thể tạo một phân tách trong tập dữ liệu với sự trợ giúp của ba phần sau:
Part1 - Tính điểm Gini: Chúng ta vừa thảo luận về phần này ở phần trước.
Part2- Tách tập dữ liệu: Nó có thể được định nghĩa là tách tập dữ liệu thành hai danh sách các hàng có chỉ số của một thuộc tính và giá trị tách của thuộc tính đó. Sau khi nhận được hai nhóm - phải và trái, từ tập dữ liệu, chúng ta có thể tính toán giá trị của phép chia bằng cách sử dụng điểm Gini được tính ở phần đầu tiên. Giá trị phân tách sẽ quyết định thuộc tính sẽ nằm trong nhóm nào.
Part3- Đánh giá tất cả các phần tách: Phần tiếp theo sau khi tìm điểm Gini và bộ dữ liệu tách là đánh giá tất cả các phần tách. Với mục đích này, trước tiên, chúng ta phải kiểm tra mọi giá trị được liên kết với từng thuộc tính dưới dạng một phân tách ứng viên. Sau đó, chúng ta cần tìm ra mức phân chia tốt nhất có thể bằng cách đánh giá chi phí của việc phân chia. Phần tách tốt nhất sẽ được sử dụng như một nút trong cây quyết định.
Xây dựng cây
Như chúng ta biết rằng một cây có nút gốc và các nút đầu cuối. Sau khi tạo nút gốc, chúng ta có thể xây dựng cây bằng hai phần sau:
Phần 1: Tạo nút đầu cuối
Trong khi tạo các nút đầu cuối của cây quyết định, một điểm quan trọng là quyết định thời điểm ngừng phát triển cây hoặc tạo các nút đầu cuối khác. Nó có thể được thực hiện bằng cách sử dụng hai tiêu chí cụ thể là độ sâu cây tối đa và bản ghi nút tối thiểu như sau:
Maximum Tree Depth- Như tên cho thấy, đây là số nút tối đa trong một cây sau nút gốc. Chúng ta phải ngừng thêm các nút đầu cuối khi một cây đạt đến độ sâu tối đa tức là khi một cây có số lượng nút đầu cuối tối đa.
Minimum Node Records- Nó có thể được định nghĩa là số lượng mẫu huấn luyện tối thiểu mà một nút nhất định chịu trách nhiệm. Chúng tôi phải ngừng thêm các nút đầu cuối khi cây đạt đến các bản ghi nút tối thiểu này hoặc dưới mức tối thiểu này.
Nút đầu cuối được sử dụng để đưa ra dự đoán cuối cùng.
Phần 2: Tách đệ quy
Như chúng ta đã hiểu về thời điểm tạo các nút đầu cuối, bây giờ chúng ta có thể bắt đầu xây dựng cây của mình. Tách đệ quy là một phương pháp để xây dựng cây. Trong phương pháp này, khi một nút được tạo, chúng ta có thể tạo các nút con (các nút được thêm vào một nút hiện có) một cách đệ quy trên mỗi nhóm dữ liệu, được tạo bằng cách tách tập dữ liệu, bằng cách gọi đi gọi lại cùng một hàm.
Sự dự đoán
Sau khi xây dựng cây quyết định, chúng ta cần đưa ra dự đoán về nó. Về cơ bản, dự đoán liên quan đến việc điều hướng cây quyết định với hàng dữ liệu được cung cấp cụ thể.
Chúng ta có thể đưa ra dự đoán với sự trợ giúp của hàm đệ quy, như đã làm ở trên. Quy trình dự đoán tương tự được gọi lại với các nút bên trái hoặc nút con bên phải.
Giả định
Sau đây là một số giả định chúng tôi đưa ra trong khi tạo cây quyết định -
Trong khi chuẩn bị cây quyết định, tập huấn luyện là nút gốc.
Bộ phân loại cây quyết định ưu tiên các giá trị tính năng được phân loại. Trong trường hợp nếu bạn muốn sử dụng các giá trị liên tục thì chúng phải được thực hiện cẩn thận trước khi xây dựng mô hình.
Dựa trên các giá trị của thuộc tính, các bản ghi được phân phối đệ quy.
Cách tiếp cận thống kê sẽ được sử dụng để đặt các thuộc tính tại bất kỳ vị trí nút nào, tức là nút gốc hoặc nút bên trong.
Triển khai bằng Python
Thí dụ
Trong ví dụ sau, chúng tôi sẽ triển khai bộ phân loại Cây Quyết định trên bệnh Tiểu đường Ấn Độ Pima -
Đầu tiên, hãy bắt đầu với việc nhập các gói python cần thiết -
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_splitTiếp theo, tải xuống tập dữ liệu mống mắt từ liên kết web của nó như sau:
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()pregnant glucose bp skin insulin bmi pedigree age label
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1Bây giờ, hãy chia tập dữ liệu thành các tính năng và biến mục tiêu như sau:
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableTiếp theo, chúng tôi sẽ chia dữ liệu thành phân chia huấn luyện và thử nghiệm. Đoạn mã sau sẽ chia tập dữ liệu thành 70% dữ liệu đào tạo và 30% dữ liệu kiểm tra -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)Tiếp theo, đào tạo mô hình với sự trợ giúp của lớp DecisionTreeClassifier của sklearn như sau:
clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)Cuối cùng, chúng ta cần phải dự đoán. Nó có thể được thực hiện với sự trợ giúp của tập lệnh sau:
y_pred = clf.predict(X_test)Tiếp theo, chúng ta có thể nhận được điểm chính xác, ma trận nhầm lẫn và báo cáo phân loại như sau:
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Đầu ra
Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
precision recall f1-score support
0 0.72 0.79 0.75 146
1 0.57 0.46 0.51 85
micro avg 0.67 0.67 0.67 231
macro avg 0.64 0.63 0.63 231
weighted avg 0.66 0.67 0.66 231
Accuracy: 0.670995670995671Hình dung cây quyết định
Cây quyết định trên có thể được hình dung với sự trợ giúp của đoạn mã sau:
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())
Giới thiệu về thuật toán Naïve Bayes
Các thuật toán Naïve Bayes là một kỹ thuật phân loại dựa trên việc áp dụng định lý Bayes với một giả định mạnh mẽ rằng tất cả các yếu tố dự đoán là độc lập với nhau. Nói cách đơn giản, giả định là sự hiện diện của một đối tượng trong một lớp là độc lập với sự hiện diện của bất kỳ đối tượng nào khác trong cùng một lớp. Ví dụ, một chiếc điện thoại có thể được coi là thông minh nếu nó có màn hình cảm ứng, tiện nghi internet, camera tốt, v.v. Mặc dù tất cả các tính năng này phụ thuộc vào nhau, chúng đóng góp độc lập vào xác suất điện thoại đó là điện thoại thông minh.
Trong phân loại Bayes, mối quan tâm chính là tìm các xác suất sau tức là xác suất của một nhãn cho một số đặc điểm quan sát được, (|). Với sự trợ giúp của định lý Bayes, chúng ta có thể biểu diễn điều này dưới dạng định lượng như sau:
$P(L |features)= \frac{P(L)P(features |L)}{()}$Ở đây, (|) là xác suất sau của lớp.
() là xác suất trước của lớp.
(|) là khả năng xảy ra là xác suất của lớp dự đoán cho trước.
() là xác suất trước của bộ dự đoán.
Xây dựng mô hình bằng Naïve Bayes trong Python
Thư viện Python, Scikit learning là thư viện hữu ích nhất giúp chúng ta xây dựng mô hình Naïve Bayes bằng Python. Chúng tôi có ba loại mô hình Naïve Bayes sau đây trong thư viện Scikit học Python:
Gaussian Naïve Bayes
Đây là bộ phân loại Naïve Bayes đơn giản nhất có giả định rằng dữ liệu từ mỗi nhãn được lấy từ một phân phối Gaussian đơn giản.
Đa thức Naïve Bayes
Một bộ phân loại Naïve Bayes hữu ích khác là Đa thức Naïve Bayes trong đó các đặc trưng được giả định là rút ra từ một phân phối Đa thức đơn giản. Loại Naïve Bayes như vậy thích hợp nhất cho các tính năng biểu thị số đếm rời rạc.
Bernoulli Naïve Bayes
Một mô hình quan trọng khác là Bernoulli Naïve Bayes, trong đó các đặc trưng được giả định là nhị phân (0 và 1). Phân loại văn bản với mô hình 'túi từ' có thể là một ứng dụng của Bernoulli Naïve Bayes.
Thí dụ
Tùy thuộc vào tập dữ liệu của chúng tôi, chúng tôi có thể chọn bất kỳ mô hình Naïve Bayes nào được giải thích ở trên. Ở đây, chúng tôi đang triển khai mô hình Gaussian Naïve Bayes bằng Python -
Chúng tôi sẽ bắt đầu với các lần nhập bắt buộc như sau:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()Bây giờ, bằng cách sử dụng hàm make_blobs () của Scikit learning, chúng ta có thể tạo ra các đốm màu với phân phối Gaussian như sau:
from sklearn.datasets import make_blobs
X, y = make_blobs(300, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');Tiếp theo, để sử dụng mô hình GaussianNB, chúng ta cần nhập và tạo đối tượng của nó như sau:
from sklearn.naive_bayes import GaussianNB
model_GBN = GaussianNB()
model_GNB.fit(X, y);Bây giờ, chúng ta phải dự đoán. Nó có thể được thực hiện sau khi tạo một số dữ liệu mới như sau:
rng = np.random.RandomState(0)
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)
ynew = model_GNB.predict(Xnew)Tiếp theo, chúng tôi đang vẽ dữ liệu mới để tìm ranh giới của nó -
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
lim = plt.axis()
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='summer', alpha=0.1)
plt.axis(lim);Bây giờ, với sự trợ giúp của dòng mã sau, chúng ta có thể tìm xác suất sau của nhãn thứ nhất và thứ hai -
yprob = model_GNB.predict_proba(Xnew)
yprob[-10:].round(3)Đầu ra
array([[0.998, 0.002],
[1. , 0. ],
[0.987, 0.013],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[0. , 1. ],
[0.986, 0.014]])Ưu & Nhược điểm
Ưu điểm
Sau đây là một số ưu điểm của việc sử dụng bộ phân loại Naïve Bayes -
Phân loại Naïve Bayes rất dễ thực hiện và nhanh chóng.
Nó sẽ hội tụ nhanh hơn các mô hình phân biệt như hồi quy logistic.
Nó yêu cầu ít dữ liệu đào tạo hơn.
Nó có khả năng mở rộng cao về bản chất, hoặc chúng chia tỷ lệ tuyến tính với số lượng các yếu tố dự đoán và điểm dữ liệu.
Nó có thể đưa ra dự đoán xác suất và có thể xử lý dữ liệu liên tục cũng như rời rạc.
Thuật toán phân loại Naïve Bayes có thể được sử dụng cho cả hai bài toán phân loại nhị phân cũng như đa lớp.
Nhược điểm
Sau đây là một số nhược điểm của việc sử dụng bộ phân loại Naïve Bayes -
Một trong những nhược điểm quan trọng nhất của phân loại Naïve Bayes là tính độc lập mạnh mẽ của nó bởi vì trong cuộc sống thực, hầu như không thể có một tập hợp các đối tượng địa lý hoàn toàn độc lập với nhau.
Một vấn đề khác với phân loại Naïve Bayes là 'tần số không' của nó, có nghĩa là nếu một biến phân loại có một danh mục nhưng không được quan sát trong tập dữ liệu huấn luyện, thì mô hình Naïve Bayes sẽ chỉ định một xác suất bằng không cho nó và nó sẽ không thể tạo ra một sự dự đoán.
Các ứng dụng của phân loại Naïve Bayes
Sau đây là một số ứng dụng phổ biến của phân loại Naïve Bayes -
Real-time prediction - Do dễ thực hiện và tính toán nhanh, nó có thể được sử dụng để dự đoán trong thời gian thực.
Multi-class prediction - Thuật toán phân loại Naïve Bayes có thể được sử dụng để dự đoán xác suất sau của nhiều lớp biến mục tiêu.
Text classification- Do tính năng của dự đoán nhiều lớp, các thuật toán phân loại của Naïve Bayes rất thích hợp cho việc phân loại văn bản. Đó là lý do tại sao nó cũng được sử dụng để giải quyết các vấn đề như lọc thư rác và phân tích tình cảm.
Recommendation system - Cùng với các thuật toán như lọc cộng tác, Naïve Bayes tạo ra một hệ thống Đề xuất có thể được sử dụng để lọc thông tin không nhìn thấy và dự đoán thời tiết mà người dùng có muốn tài nguyên đã cho hay không.
Giới thiệu
Rừng ngẫu nhiên là một thuật toán học có giám sát được sử dụng cho cả phân loại cũng như hồi quy. Tuy nhiên, nó chủ yếu được sử dụng cho các bài toán phân loại. Như chúng ta biết rằng một khu rừng được tạo thành từ cây cối và nhiều cây cối hơn có nghĩa là khu rừng vững chắc hơn. Tương tự, thuật toán rừng ngẫu nhiên tạo ra các cây quyết định trên các mẫu dữ liệu và sau đó lấy dự đoán từ mỗi người trong số chúng và cuối cùng chọn giải pháp tốt nhất bằng cách bỏ phiếu. Đây là một phương pháp tổng hợp tốt hơn một cây quyết định đơn lẻ vì nó làm giảm sự phù hợp quá mức bằng cách lấy trung bình kết quả.
Hoạt động của thuật toán rừng ngẫu nhiên
Chúng ta có thể hiểu hoạt động của thuật toán Rừng ngẫu nhiên với sự trợ giúp của các bước sau:
Step1 - Đầu tiên, hãy bắt đầu với việc chọn các mẫu ngẫu nhiên từ một tập dữ liệu nhất định.
Step2- Tiếp theo, thuật toán này sẽ xây dựng một cây quyết định cho mọi mẫu. Sau đó, nó sẽ nhận được kết quả dự đoán từ mọi cây quyết định.
Step3 - Ở bước này, sẽ thực hiện bình chọn cho mọi kết quả dự đoán.
Step4 - Cuối cùng, chọn kết quả dự đoán được bình chọn nhiều nhất làm kết quả dự đoán cuối cùng.
Sơ đồ sau đây sẽ minh họa hoạt động của nó:

Triển khai bằng Python
Đầu tiên, hãy bắt đầu với việc nhập các gói Python cần thiết -
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdTiếp theo, tải xuống tập dữ liệu mống mắt từ liên kết web của nó như sau:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Tiếp theo, chúng ta cần gán tên cột cho tập dữ liệu như sau:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Bây giờ, chúng ta cần đọc tập dữ liệu thành khung dữ liệu gấu trúc như sau:
dataset = pd.read_csv(path, names=headernames)
dataset.head()lá đài dài |
chiều rộng đài hoa |
chiều dài cánh hoa |
chiều rộng cánh hoa |
Lớp học |
|
|---|---|---|---|---|---|
0 |
5.1 |
3.5 |
1,4 |
0,2 |
Iris-setosa |
1 |
4,9 |
3.0 |
1,4 |
0,2 |
Iris-setosa |
2 |
4,7 |
3.2 |
1,3 |
0,2 |
Iris-setosa |
3 |
4,6 |
3.1 |
1,5 |
0,2 |
Iris-setosa |
4 |
5.0 |
3.6 |
1,4 |
0,2 |
Iris-setosa |
Quá trình tiền xử lý dữ liệu sẽ được thực hiện với sự trợ giúp của các dòng tập lệnh sau:
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].valuesTiếp theo, chúng tôi sẽ chia dữ liệu thành phân chia huấn luyện và thử nghiệm. Đoạn mã sau sẽ chia tập dữ liệu thành 70% dữ liệu đào tạo và 30% dữ liệu kiểm tra -
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)Tiếp theo, đào tạo mô hình với sự trợ giúp của lớp RandomForestClassifier của sklearn như sau:
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(n_estimators=50)
classifier.fit(X_train, y_train)Cuối cùng, chúng ta cần phải dự đoán. Nó có thể được thực hiện với sự trợ giúp của tập lệnh sau:
y_pred = classifier.predict(X_test)Tiếp theo, in kết quả như sau:
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Đầu ra
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777Ưu và nhược điểm của Rừng ngẫu nhiên
Ưu điểm
Sau đây là những ưu điểm của thuật toán Rừng ngẫu nhiên -
Nó khắc phục vấn đề overfitting bằng cách lấy trung bình hoặc kết hợp các kết quả của các cây quyết định khác nhau.
Rừng ngẫu nhiên hoạt động tốt cho một loạt các mục dữ liệu hơn là một cây quyết định đơn lẻ.
Rừng ngẫu nhiên có ít phương sai hơn so với cây quyết định duy nhất.
Rừng ngẫu nhiên rất linh hoạt và có độ chính xác rất cao.
Việc chia tỷ lệ dữ liệu không yêu cầu trong thuật toán rừng ngẫu nhiên. Nó duy trì độ chính xác tốt ngay cả sau khi cung cấp dữ liệu mà không mở rộng quy mô.
Việc chia tỷ lệ dữ liệu không yêu cầu trong thuật toán rừng ngẫu nhiên. Nó duy trì độ chính xác tốt ngay cả sau khi cung cấp dữ liệu mà không mở rộng quy mô.
Nhược điểm
Sau đây là những nhược điểm của thuật toán Rừng ngẫu nhiên -
Sự phức tạp là nhược điểm chính của các thuật toán Rừng ngẫu nhiên.
Việc xây dựng Rừng ngẫu nhiên khó và tốn thời gian hơn nhiều so với cây quyết định.
Cần nhiều tài nguyên tính toán hơn để triển khai thuật toán Rừng ngẫu nhiên.
Nó kém trực quan hơn trong trường hợp chúng ta có một bộ sưu tập lớn các cây quyết định.
Quá trình dự đoán bằng cách sử dụng các khu rừng ngẫu nhiên rất tốn thời gian so với các thuật toán khác.
Giới thiệu về hồi quy
Hồi quy là một công cụ thống kê và máy học quan trọng và được sử dụng rộng rãi. Mục tiêu chính của các tác vụ dựa trên hồi quy là dự đoán các nhãn hoặc phản hồi đầu ra là các giá trị số tiếp tục, cho dữ liệu đầu vào đã cho. Đầu ra sẽ dựa trên những gì mô hình đã học được trong giai đoạn đào tạo. Về cơ bản, các mô hình hồi quy sử dụng các đặc trưng dữ liệu đầu vào (các biến độc lập) và các giá trị đầu ra số liên tục tương ứng của chúng (biến phụ thuộc hoặc kết quả) để tìm hiểu mối liên hệ cụ thể giữa đầu vào và đầu ra tương ứng.

Các loại mô hình hồi quy

Mô hình hồi quy có hai loại sau:
Simple regression model - Đây là mô hình hồi quy cơ bản nhất trong đó các dự đoán được hình thành từ một đặc điểm duy nhất, đơn biến của dữ liệu.
Multiple regression model - Như tên của nó, trong mô hình hồi quy này, các dự đoán được hình thành từ nhiều đặc điểm của dữ liệu.
Xây dựng Regressor bằng Python
Mô hình bộ hồi quy trong Python có thể được xây dựng giống như chúng ta đã xây dựng bộ phân loại. Scikit-learning, một thư viện Python dành cho học máy cũng có thể được sử dụng để xây dựng một bộ hồi quy bằng Python.
Trong ví dụ sau, chúng tôi sẽ xây dựng mô hình hồi quy cơ bản sẽ phù hợp với một dòng với dữ liệu tức là hồi quy tuyến tính. Các bước cần thiết để xây dựng một bộ hồi quy trong Python như sau:
Bước 1: Nhập gói python cần thiết
Để xây dựng một bộ hồi quy bằng scikit-learning, chúng ta cần nhập nó cùng với các gói cần thiết khác. Chúng tôi có thể nhập bằng cách sử dụng tập lệnh sau:
import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as pltBước 2: Nhập tập dữ liệu
Sau khi nhập gói cần thiết, chúng ta cần một tập dữ liệu để xây dựng mô hình dự đoán hồi quy. Chúng tôi có thể nhập nó từ tập dữ liệu sklearn hoặc có thể sử dụng tập dữ liệu khác theo yêu cầu của chúng tôi. Chúng tôi sẽ sử dụng dữ liệu đầu vào đã lưu của chúng tôi. Chúng tôi có thể nhập nó với sự trợ giúp của tập lệnh sau:
input = r'C:\linear.txt'Tiếp theo, chúng ta cần tải dữ liệu này. Chúng tôi đang sử dụng hàm np.loadtxt để tải nó.
input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]Bước 3: Tổ chức dữ liệu thành các bộ đào tạo và kiểm tra
Do đó, chúng tôi cần kiểm tra mô hình của mình trên dữ liệu không nhìn thấy, chúng tôi sẽ chia tập dữ liệu của mình thành hai phần: tập huấn luyện và tập thử nghiệm. Lệnh sau sẽ thực hiện nó:
training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]Bước 4- Đánh giá và dự đoán mô hình
Sau khi phân chia dữ liệu thành đào tạo và thử nghiệm, chúng ta cần xây dựng mô hình. Chúng tôi sẽ sử dụng hàm LineaRegression () của Scikit-learning cho mục đích này. Lệnh sau sẽ tạo một đối tượng hồi quy tuyến tính.
reg_linear= linear_model.LinearRegression()Tiếp theo, đào tạo mô hình này với các mẫu đào tạo như sau:
reg_linear.fit(X_train, y_train)Bây giờ, cuối cùng chúng ta cần thực hiện dự đoán với dữ liệu thử nghiệm.
y_test_pred = reg_linear.predict(X_test)Bước 5- Âm mưu & hình dung
Sau khi dự đoán, chúng ta có thể vẽ và hình dung nó với sự trợ giúp của tập lệnh sau:
plt.scatter(X_test, y_test, color='red')
plt.plot(X_test, y_test_pred, color='black', linewidth=2)
plt.xticks(())
plt.yticks(())
plt.show()Đầu ra

Trong kết quả trên, chúng ta có thể thấy đường hồi quy giữa các điểm dữ liệu.
Step6- Performance computation - Chúng tôi cũng có thể tính toán hiệu suất của mô hình hồi quy của mình với sự trợ giúp của các số liệu hiệu suất khác nhau như sau:
print("Regressor model performance:")
print("Mean absolute error(MAE) =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error(MSE) =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))Đầu ra
Regressor model performance:
Mean absolute error(MAE) = 1.78
Mean squared error(MSE) = 3.89
Median absolute error = 2.01
Explain variance score = -0.09
R2 score = -0.09Các loại thuật toán hồi quy ML
Thuật toán hồi quy ML hữu ích và phổ biến nhất là thuật toán hồi quy tuyến tính được chia thành hai loại cụ thể là:
Thuật toán hồi quy tuyến tính đơn giản
Thuật toán hồi quy nhiều tuyến tính.
Chúng ta sẽ thảo luận về nó và triển khai nó bằng Python trong chương tiếp theo.
Các ứng dụng
Các ứng dụng của thuật toán hồi quy ML như sau:
Forecasting or Predictive analysis- Một trong những ứng dụng quan trọng của hồi quy là dự báo hoặc phân tích dự báo. Ví dụ, chúng ta có thể dự báo GDP, giá dầu hay nói cách đơn giản là dữ liệu định lượng thay đổi theo thời gian.
Optimization- Chúng tôi có thể tối ưu hóa các quy trình kinh doanh với sự trợ giúp của hồi quy. Ví dụ: một người quản lý cửa hàng có thể tạo một mô hình thống kê để hiểu thời gian đến của khách hàng.
Error correction- Trong kinh doanh, việc đưa ra quyết định đúng đắn cũng quan trọng không kém việc tối ưu hóa quy trình kinh doanh. Hồi quy có thể giúp chúng ta đưa ra quyết định chính xác cũng như điều chỉnh quyết định đã được thực hiện.
Economics- Nó là công cụ được sử dụng nhiều nhất trong kinh tế học. Chúng ta có thể sử dụng hồi quy để dự đoán cung, cầu, tiêu dùng, đầu tư hàng tồn kho, v.v.
Finance- Một công ty tài chính luôn quan tâm đến việc giảm thiểu danh mục rủi ro và muốn biết các yếu tố ảnh hưởng đến khách hàng. Tất cả những điều này có thể được dự đoán với sự trợ giúp của mô hình hồi quy.
Giới thiệu về hồi quy tuyến tính
Hồi quy tuyến tính có thể được định nghĩa là mô hình thống kê phân tích mối quan hệ tuyến tính giữa một biến phụ thuộc với một tập hợp các biến độc lập nhất định. Mối quan hệ tuyến tính giữa các biến có nghĩa là khi giá trị của một hoặc nhiều biến độc lập sẽ thay đổi (tăng hoặc giảm) thì giá trị của biến phụ thuộc cũng thay đổi theo (tăng hoặc giảm).
Về mặt toán học, mối quan hệ có thể được biểu diễn với sự trợ giúp của phương trình sau:
Y = mX + b
Ở đây, Y là biến phụ thuộc mà chúng tôi đang cố gắng dự đoán
X là biến phụ thuộc mà chúng tôi đang sử dụng để đưa ra dự đoán.
m là độ dốc của đường hồi quy thể hiện tác động của X đối với Y
b là một hằng số, được gọi là Y-intercept. Nếu X = 0, Y sẽ bằng b.
Hơn nữa, mối quan hệ tuyến tính có thể có bản chất tích cực hoặc tiêu cực như được giải thích dưới đây:
Mối quan hệ tuyến tính tích cực
Một mối quan hệ tuyến tính sẽ được gọi là dương nếu cả biến độc lập và biến phụ thuộc đều tăng. Nó có thể được hiểu với sự trợ giúp của đồ thị sau:

Mối quan hệ tuyến tính phủ định
Một mối quan hệ tuyến tính sẽ được gọi là dương nếu biến độc lập tăng và biến phụ thuộc giảm. Nó có thể được hiểu với sự trợ giúp của đồ thị sau:

Các loại hồi quy tuyến tính
Hồi quy tuyến tính có hai loại sau:
Hồi quy tuyến tính cơ bản
Hồi quy nhiều tuyến tính
Hồi quy tuyến tính đơn giản (SLR)
Đây là phiên bản cơ bản nhất của hồi quy tuyến tính dự đoán phản hồi bằng cách sử dụng một tính năng duy nhất. Giả định trong SLR là hai biến có liên quan tuyến tính.
Triển khai Python
Chúng ta có thể triển khai SLR bằng Python theo hai cách, một là cung cấp tập dữ liệu của riêng bạn và cách khác là sử dụng tập dữ liệu từ thư viện python scikit-learning.
Example1 - Trong ví dụ triển khai Python sau đây, chúng tôi đang sử dụng tập dữ liệu của riêng mình.
Đầu tiên, chúng ta sẽ bắt đầu với việc nhập các gói cần thiết như sau:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltTiếp theo, xác định một hàm sẽ tính toán các giá trị quan trọng cho SLR -
def coef_estimation(x, y):Dòng kịch bản sau đây sẽ cung cấp số lượng quan sát n -
n = np.size(x)Giá trị trung bình của vectơ x và y có thể được tính như sau:
m_x, m_y = np.mean(x), np.mean(y)Chúng ta có thể tìm thấy độ lệch chéo và độ lệch về x như sau:
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xTiếp theo, các hệ số hồi quy tức là b có thể được tính như sau:
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)Tiếp theo, chúng ta cần xác định một hàm sẽ vẽ đường hồi quy cũng như sẽ dự đoán vectơ phản hồi -
def plot_regression_line(x, y, b):Dòng kịch bản sau sẽ vẽ các điểm thực tế dưới dạng âm mưu phân tán -
plt.scatter(x, y, color = "m", marker = "o", s = 30)Dòng script sau sẽ dự đoán vectơ phản hồi -
y_pred = b[0] + b[1]*xCác dòng kịch bản sau sẽ vẽ dòng hồi quy và sẽ dán nhãn lên chúng -
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()Cuối cùng, chúng ta cần xác định hàm main () để cung cấp tập dữ liệu và gọi hàm mà chúng ta đã xác định ở trên -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()Đầu ra
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788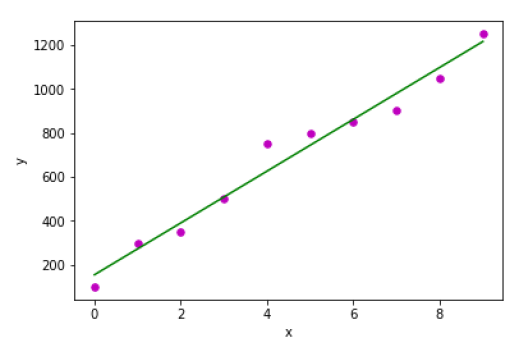
Example2 - Trong ví dụ triển khai Python sau đây, chúng tôi đang sử dụng tập dữ liệu bệnh tiểu đường từ scikit-learning.
Đầu tiên, chúng ta sẽ bắt đầu với việc nhập các gói cần thiết như sau:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreTiếp theo, chúng tôi sẽ tải tập dữ liệu bệnh tiểu đường và tạo đối tượng của nó -
diabetes = datasets.load_diabetes()Khi chúng tôi đang triển khai SLR, chúng tôi sẽ chỉ sử dụng một tính năng như sau:
X = diabetes.data[:, np.newaxis, 2]Tiếp theo, chúng ta cần chia dữ liệu thành các tập huấn luyện và thử nghiệm như sau:
X_train = X[:-30]
X_test = X[-30:]Tiếp theo, chúng ta cần chia mục tiêu thành các nhóm đào tạo và kiểm tra như sau:
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]Bây giờ, để đào tạo mô hình, chúng ta cần tạo đối tượng hồi quy tuyến tính như sau:
regr = linear_model.LinearRegression()Tiếp theo, huấn luyện mô hình bằng cách sử dụng các tập huấn luyện như sau:
regr.fit(X_train, y_train)Tiếp theo, đưa ra dự đoán bằng cách sử dụng bộ thử nghiệm như sau:
y_pred = regr.predict(X_test)Tiếp theo, chúng tôi sẽ in một số hệ số như MSE, điểm phương sai, v.v. như sau:
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f"
% mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))Bây giờ, vẽ biểu đồ đầu ra như sau:
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()Đầu ra
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Hồi quy nhiều tuyến tính (MLR)
Nó là phần mở rộng của hồi quy tuyến tính đơn giản dự đoán một phản hồi bằng cách sử dụng hai hoặc nhiều tính năng. Về mặt toán học, chúng ta có thể giải thích nó như sau:
Xem xét một tập dữ liệu có n quan sát, p đặc trưng tức là biến độc lập và y là một phản hồi tức là biến phụ thuộc, đường hồi quy cho p đặc trưng có thể được tính như sau:
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}$Ở đây, h (x i ) là giá trị phản hồi dự đoán và b 0 , b 1 , b 2 â € ¦, b p là các hệ số hồi quy.
Nhiều mô hình hồi quy tuyến tính luôn bao gồm các lỗi trong dữ liệu được gọi là lỗi dư, điều này làm thay đổi phép tính như sau:
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}+e_{i}$Chúng ta cũng có thể viết phương trình trên như sau:
$y_{i}=h(x_{i})+e_{i}$ $e_{i}= y_{i} - h(x_{i})$Triển khai Python
trong ví dụ này, chúng tôi sẽ sử dụng tập dữ liệu nhà ở Boston từ scikit learning -
Đầu tiên, chúng ta sẽ bắt đầu với việc nhập các gói cần thiết như sau:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsTiếp theo, tải tập dữ liệu như sau:
boston = datasets.load_boston(return_X_y=False)Các dòng script sau sẽ xác định ma trận đặc trưng, X và vectơ phản hồi, Y -
X = boston.data
y = boston.targetTiếp theo, chia tập dữ liệu thành các tập huấn luyện và thử nghiệm như sau:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)Bây giờ, tạo đối tượng hồi quy tuyến tính và huấn luyện mô hình như sau:
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()Đầu ra
Coefficients:
[-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01]
Variance score: 0.709454060230326
Giả định
Sau đây là một số giả định về tập dữ liệu được thực hiện bởi mô hình hồi quy tuyến tính:
Multi-collinearity- Mô hình hồi quy tuyến tính giả định rằng có rất ít hoặc không có tính đa cộng tuyến trong dữ liệu. Về cơ bản, đa cộng tuyến xảy ra khi các biến hoặc đặc trưng độc lập có sự phụ thuộc vào chúng.
Auto-correlation- Một giả định khác Mô hình hồi quy tuyến tính giả định là có rất ít hoặc không có tương quan tự động trong dữ liệu. Về cơ bản, tự động tương quan xảy ra khi có sự phụ thuộc giữa các sai số dư.
Relationship between variables - Mô hình hồi quy tuyến tính giả định rằng mối quan hệ giữa các biến phản hồi và đặc trưng phải là tuyến tính.
Giới thiệu về phân cụm
Các phương pháp phân cụm là một trong những phương pháp ML không giám sát hữu ích nhất. Các phương pháp này được sử dụng để tìm sự tương đồng cũng như các mẫu mối quan hệ giữa các mẫu dữ liệu và sau đó phân cụm các mẫu đó thành các nhóm có sự tương đồng dựa trên các tính năng.
Phân cụm rất quan trọng vì nó quyết định việc nhóm nội tại giữa các dữ liệu không được gắn nhãn hiện tại. Về cơ bản, họ đưa ra một số giả định về các điểm dữ liệu để tạo nên sự giống nhau của chúng. Mỗi giả định sẽ xây dựng các cụm khác nhau nhưng đều hợp lệ.
Ví dụ: dưới đây là sơ đồ cho thấy hệ thống phân cụm được nhóm cùng loại dữ liệu tương tự trong các cụm khác nhau -

Phương pháp hình thành cụm
Không nhất thiết các cụm sẽ được hình thành ở dạng hình cầu. Tiếp theo là một số phương pháp hình thành cụm khác -
Dựa trên mật độ
Trong các phương pháp này, các cụm được hình thành dưới dạng vùng dày đặc. Ưu điểm của các phương pháp này là có độ chính xác cũng như khả năng ghép hai cụm tốt. Ví dụ. Phân cụm không gian dựa trên mật độ của các ứng dụng có tiếng ồn (DBSCAN), Điểm thứ tự để xác định cấu trúc phân cụm (OPTICS), v.v.
Dựa trên phân cấp
Trong các phương pháp này, các cụm được hình thành như một cấu trúc kiểu cây dựa trên hệ thống phân cấp. Chúng có hai loại cụ thể là Agglomerative (Cách tiếp cận từ dưới lên) và Phân chia (Cách tiếp cận từ trên xuống). Ví dụ. Phân cụm bằng cách sử dụng Đại diện (CURE), Phân cụm lặp lại cân bằng Giảm phân cụm bằng cách sử dụng Cấu trúc phân cấp (BIRCH), v.v.
Phân vùng
Trong các phương pháp này, các cụm được hình thành bằng cách phân chia các đối tượng thành k cụm. Số lượng cụm sẽ bằng số lượng phân vùng. Ví dụ. K-means, Nhóm các ứng dụng lớn dựa trên Tìm kiếm ngẫu nhiên (CLARANS).
Lưới
Trong các phương pháp này, các cụm được hình thành như một cấu trúc giống như lưới. Ưu điểm của các phương pháp này là tất cả các hoạt động phân cụm được thực hiện trên các lưới này là nhanh chóng và không phụ thuộc vào số lượng đối tượng dữ liệu. Ví dụ. Lưới thông tin thống kê (STING), Nhóm trong nhiệm vụ (CLIQUE).
Đo lường hiệu suất phân cụm
Một trong những cân nhắc quan trọng nhất liên quan đến mô hình ML là đánh giá hiệu suất của nó hoặc bạn có thể nói chất lượng của mô hình. Trong trường hợp thuật toán học có giám sát, việc đánh giá chất lượng mô hình của chúng tôi rất dễ dàng vì chúng tôi đã có nhãn cho mọi ví dụ.
Mặt khác, trong trường hợp các thuật toán học tập không được giám sát, chúng tôi không có nhiều may mắn vì chúng tôi xử lý dữ liệu không được gắn nhãn. Nhưng chúng tôi vẫn có một số số liệu cung cấp cho người thực hành cái nhìn sâu sắc về sự thay đổi trong các cụm tùy thuộc vào thuật toán.
Trước khi đi sâu vào các số liệu như vậy, chúng ta phải hiểu rằng các số liệu này chỉ đánh giá hiệu suất so sánh của các mô hình với nhau chứ không phải đo lường tính hợp lệ của dự đoán của mô hình. Tiếp theo là một số chỉ số mà chúng tôi có thể triển khai trên các thuật toán phân cụm để đo chất lượng của mô hình -
Phân tích Silhouette
Phân tích Silhouette được sử dụng để kiểm tra chất lượng của mô hình phân cụm bằng cách đo khoảng cách giữa các cụm. Về cơ bản, nó cung cấp cho chúng tôi một cách để đánh giá các thông số như số lượng cụm với sự trợ giúp củaSilhouette score. Điểm này đo lường mức độ gần của mỗi điểm trong một cụm với các điểm trong các cụm lân cận.
Phân tích điểm Silhouette
Phạm vi của điểm Silhouette là [-1, 1]. Phân tích của nó như sau:
+1 Score - Gần +1 Silhouette score chỉ ra rằng mẫu ở xa cụm lân cận của nó.
0 Score - 0 Silhouette score chỉ ra rằng mẫu nằm trên hoặc rất gần ranh giới quyết định ngăn cách hai cụm lân cận.
-1 Score & trừ đi -1 Silhouette score chỉ ra rằng các mẫu đã được chỉ định vào các cụm sai.
Việc tính điểm Silhouette có thể được thực hiện bằng công thức sau:
= (-) / (,)
Đây, = khoảng cách trung bình đến các điểm trong cụm gần nhất
Và, = nghĩa là khoảng cách trong cụm đến tất cả các điểm.
Chỉ số Davis-Bouldin
Chỉ số DB là một số liệu tốt khác để thực hiện phân tích các thuật toán phân cụm. Với sự trợ giúp của chỉ mục DB, chúng ta có thể hiểu những điểm sau về mô hình phân cụm:
Thời tiết các cụm có cách xa nhau hay không?
Mật độ của các cụm là bao nhiêu?
Chúng ta có thể tính toán chỉ số DB với sự trợ giúp của công thức sau:
$DB=\frac{1}{n}\displaystyle\sum\limits_{i=1}^n max_{j\neq{i}}\left(\frac{\sigma_{i}+\sigma_{j}}{d(c_{i},c_{j})}\right)$Đây, = số cụm
σ i = khoảng cách trung bình của tất cả các điểm trong cụm tính từ trung tâm cụm.
Chỉ số DB ít hơn, mô hình phân cụm tốt hơn.
Chỉ số Dunn
Nó hoạt động giống như chỉ mục DB nhưng có những điểm sau mà cả hai đều khác nhau:
Chỉ số Dunn chỉ xem xét trường hợp xấu nhất tức là các cụm gần nhau trong khi chỉ số DB xem xét sự phân tán và tách biệt của tất cả các cụm trong mô hình phân cụm.
Chỉ số Dunn tăng khi hiệu suất tăng lên trong khi chỉ số DB trở nên tốt hơn khi các cụm có khoảng cách tốt và dày đặc.
Chúng ta có thể tính toán chỉ số Dunn với sự trợ giúp của công thức sau:
$D=\frac{min_{1\leq i <{j}\leq{n}}P(i,j)}{mix_{1\leq i < k \leq n}q(k)}$Đây, ,, = mỗi chỉ số cho các cụm
= khoảng cách giữa các cụm
q = khoảng cách trong cụm
Các loại thuật toán phân cụm ML
Sau đây là các thuật toán phân cụm ML quan trọng và hữu ích nhất -
K-có nghĩa là phân cụm
Thuật toán phân cụm này tính toán các centroid và lặp lại cho đến khi chúng tôi tìm thấy centroid tối ưu. Nó giả định rằng số lượng các cụm đã được biết trước. Nó còn được gọi là thuật toán phân cụm phẳng. Số lượng các cụm được xác định từ dữ liệu bằng thuật toán được biểu thị bằng 'K' trong K-mean.
Thuật toán Mean-Shift
Nó là một thuật toán phân cụm mạnh mẽ khác được sử dụng trong học tập không giám sát. Không giống như K-mean clustering, nó không đưa ra bất kỳ giả định nào do đó nó là một thuật toán phi tham số.
Phân cụm theo thứ bậc
Đó là một thuật toán học tập không giám sát khác được sử dụng để nhóm các điểm dữ liệu không được gắn nhãn có đặc điểm tương tự lại với nhau.
Chúng ta sẽ thảo luận chi tiết về tất cả các thuật toán này trong các chương sắp tới.
Các ứng dụng của phân cụm
Chúng ta có thể thấy phân cụm hữu ích trong các lĩnh vực sau:
Data summarization and compression- Phân cụm được sử dụng rộng rãi trong các lĩnh vực mà chúng ta yêu cầu tổng hợp, nén và giảm dữ liệu. Các ví dụ là xử lý hình ảnh và lượng tử hóa vector.
Collaborative systems and customer segmentation - Vì phân cụm có thể được sử dụng để tìm các sản phẩm tương tự hoặc cùng một loại người dùng, nó có thể được sử dụng trong lĩnh vực hệ thống cộng tác và phân khúc khách hàng.
Serve as a key intermediate step for other data mining tasks- Phân tích cụm có thể tạo ra một bản tóm tắt dữ liệu nhỏ gọn để phân loại, kiểm tra, tạo giả thuyết; do đó, nó cũng đóng vai trò là bước trung gian quan trọng cho các tác vụ khai thác dữ liệu khác.
Trend detection in dynamic data - Phân cụm cũng có thể được sử dụng để phát hiện xu hướng trong dữ liệu động bằng cách tạo các cụm xu hướng tương tự khác nhau.
Social network analysis- Phân cụm có thể được sử dụng trong phân tích mạng xã hội. Các ví dụ đang tạo chuỗi trong hình ảnh, video hoặc âm thanh.
Biological data analysis - Phân cụm cũng có thể được sử dụng để tạo thành các cụm hình ảnh, video do đó nó có thể được sử dụng thành công trong phân tích dữ liệu sinh học.
Giới thiệu về thuật toán K-Means
Thuật toán phân cụm K-mean tính toán các centroid và lặp lại cho đến khi chúng tôi tìm thấy centroid tối ưu. Nó giả định rằng số lượng các cụm đã được biết trước. Nó còn được gọi làflat clusteringthuật toán. Số lượng các cụm được xác định từ dữ liệu bằng thuật toán được biểu thị bằng 'K' trong K-mean.
Trong thuật toán này, các điểm dữ liệu được gán cho một cụm sao cho tổng khoảng cách bình phương giữa các điểm dữ liệu và centroid sẽ là nhỏ nhất. Cần phải hiểu rằng ít biến động hơn trong các cụm sẽ dẫn đến nhiều điểm dữ liệu giống nhau hơn trong cùng một cụm.
Hoạt động của thuật toán K-Means
Chúng ta có thể hiểu hoạt động của thuật toán phân cụm K-Means với sự trợ giúp của các bước sau:
Step1 - Đầu tiên, chúng ta cần xác định số lượng cụm, K, cần được tạo ra bởi thuật toán này.
Step2- Tiếp theo, chọn ngẫu nhiên K điểm dữ liệu và gán mỗi điểm dữ liệu vào một cụm. Nói cách đơn giản, hãy phân loại dữ liệu dựa trên số điểm dữ liệu.
Step3 - Bây giờ nó sẽ tính toán các trung tâm cụm.
Step4 - Tiếp theo, tiếp tục lặp lại các bước sau cho đến khi chúng ta tìm thấy centroid tối ưu, đó là việc gán các điểm dữ liệu cho các cụm không thay đổi nữa -
4.1 - Đầu tiên, tổng bình phương khoảng cách giữa các điểm dữ liệu và trung tâm sẽ được tính toán.
4.2 - Bây giờ, chúng ta phải gán mỗi điểm dữ liệu cho cụm gần hơn cụm khác (centroid).
4.3 - Cuối cùng, tính toán trọng tâm cho các cụm bằng cách lấy giá trị trung bình của tất cả các điểm dữ liệu của cụm đó.
K-mean theo sau Expectation-Maximizationcách tiếp cận để giải quyết vấn đề. Bước Kỳ vọng được sử dụng để gán các điểm dữ liệu cho cụm gần nhất và bước Tối đa hóa được sử dụng để tính toán trung tâm của mỗi cụm.
Trong khi làm việc với thuật toán K-mean, chúng ta cần lưu ý những điều sau:
Trong khi làm việc với các thuật toán phân cụm bao gồm K-Means, bạn nên chuẩn hóa dữ liệu vì các thuật toán như vậy sử dụng phép đo dựa trên khoảng cách để xác định sự giống nhau giữa các điểm dữ liệu.
Do tính chất lặp đi lặp lại của K-Means và sự khởi tạo ngẫu nhiên của các trung tâm, K-Means có thể gắn bó với mức tối ưu cục bộ và có thể không hội tụ với mức tối ưu toàn cục. Đó là lý do tại sao nó được khuyến khích sử dụng các khởi tạo khác nhau của centroid.
Triển khai bằng Python
Hai ví dụ sau đây về việc triển khai thuật toán phân cụm K-Means sẽ giúp chúng ta hiểu rõ hơn về nó -
Ví dụ 1
Đó là một ví dụ đơn giản để hiểu cách hoạt động của k-mean. Trong ví dụ này, trước tiên chúng ta sẽ tạo tập dữ liệu 2D chứa 4 đốm màu khác nhau và sau đó sẽ áp dụng thuật toán k-mean để xem kết quả.
Đầu tiên, chúng tôi sẽ bắt đầu bằng cách nhập các gói cần thiết -
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeansĐoạn mã sau sẽ tạo 2D, chứa bốn đốm màu -
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)Tiếp theo, đoạn mã sau sẽ giúp chúng ta hình dung tập dữ liệu:
plt.scatter(X[:, 0], X[:, 1], s=20);
plt.show()
Tiếp theo, tạo một đối tượng của KMeans cùng với việc cung cấp số lượng cụm, đào tạo mô hình và thực hiện dự đoán như sau:
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)Bây giờ, với sự trợ giúp của đoạn mã sau, chúng ta có thể vẽ và hình dung các trung tâm của cụm được chọn bởi trình ước lượng Python k-mean -
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9);
plt.show()
Ví dụ 2
Chúng ta hãy chuyển sang một ví dụ khác, trong đó chúng ta sẽ áp dụng phân cụm K-mean trên tập dữ liệu các chữ số đơn giản. K-means sẽ cố gắng xác định các chữ số tương tự mà không cần sử dụng thông tin nhãn gốc.
Đầu tiên, chúng tôi sẽ bắt đầu bằng cách nhập các gói cần thiết -
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeansTiếp theo, tải tập dữ liệu chữ số từ sklearn và tạo một đối tượng của nó. Chúng ta cũng có thể tìm số hàng và số cột trong tập dữ liệu này như sau:
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shapeĐầu ra
(1797, 64)Kết quả trên cho thấy tập dữ liệu này có 1797 mẫu với 64 tính năng.
Chúng ta có thể thực hiện phân cụm như đã làm trong Ví dụ 1 ở trên -
kmeans = KMeans(n_clusters=10, random_state=0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shapeĐầu ra
(10, 64)Kết quả trên cho thấy K-mean đã tạo ra 10 cụm với 64 tính năng.
fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)Đầu ra
Như đầu ra, chúng ta sẽ nhận được hình ảnh sau đây cho thấy các trung tâm cụm được học bằng k-means.

Các dòng mã sau sẽ khớp các nhãn cụm đã học với các nhãn thực được tìm thấy trong chúng -
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]Tiếp theo, chúng ta có thể kiểm tra độ chính xác như sau:
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Đầu ra
0.7935447968836951Kết quả trên cho thấy độ chính xác là khoảng 80%.
Ưu điểm và nhược điểm
Ưu điểm
Sau đây là một số ưu điểm của thuật toán phân cụm K-Means:
Nó rất dễ hiểu và dễ thực hiện.
Nếu chúng ta có số lượng biến lớn thì K-mean sẽ nhanh hơn so với phân cụm phân cấp.
Khi tính toán lại các centroid, một thể hiện có thể thay đổi cụm.
Các cụm chặt chẽ hơn được hình thành với K-means so với phân cụm theo thứ bậc.
Nhược điểm
Sau đây là một số nhược điểm của thuật toán phân cụm K-Means:
Có một chút khó khăn để dự đoán số lượng cụm tức là giá trị của k.
Đầu ra bị tác động mạnh bởi các đầu vào ban đầu như số cụm (giá trị của k).
Thứ tự của dữ liệu sẽ có tác động mạnh mẽ đến kết quả cuối cùng.
Nó rất nhạy cảm với việc thay đổi tỷ lệ. Nếu chúng tôi bán lại dữ liệu của mình bằng phương pháp chuẩn hóa hoặc chuẩn hóa, thì đầu ra sẽ hoàn toàn thay đổi. Đầu ra cuối cùng.
Sẽ không tốt khi thực hiện công việc phân cụm nếu các cụm có dạng hình học phức tạp.
Các ứng dụng của K-Means Clustering Algorithm
Các mục tiêu chính của phân tích cụm là -
Để có được trực giác có ý nghĩa từ dữ liệu chúng tôi đang làm việc.
Cluster-then-dự đoán nơi các mô hình khác nhau sẽ được xây dựng cho các nhóm con khác nhau.
Để hoàn thành các mục tiêu đề cập ở trên, K-means clustering đang hoạt động đủ tốt. Nó có thể được sử dụng trong các ứng dụng sau:
Phân khúc thị trường
Phân cụm tài liệu
Phân đoạn hình ảnh
Nén hình ảnh
Phân khúc khách hàng
Phân tích xu hướng trên dữ liệu động
Giới thiệu về thuật toán Mean-Shift
Như đã thảo luận trước đó, nó là một thuật toán phân cụm mạnh mẽ khác được sử dụng trong học tập không giám sát. Không giống như K-mean clustering, nó không đưa ra bất kỳ giả định nào; do đó nó là một thuật toán không tham số.
Thuật toán Mean-shift về cơ bản chỉ định lặp đi lặp lại các điểm dữ liệu cho các cụm bằng cách dịch chuyển các điểm về phía mật độ điểm dữ liệu cao nhất tức là trung tâm cụm.
Sự khác biệt giữa thuật toán K-Means và Mean-Shift là sau này người ta không cần chỉ định trước số lượng cụm vì số lượng cụm sẽ được xác định bởi dữ liệu wrt của thuật toán.
Hoạt động của thuật toán Mean-Shift
Chúng ta có thể hiểu hoạt động của thuật toán phân cụm Mean-Shift với sự trợ giúp của các bước sau:
Step1 - Đầu tiên, hãy bắt đầu với các điểm dữ liệu được gán cho một cụm của riêng chúng.
Step2 - Tiếp theo, thuật toán này sẽ tính toán các centroid.
Step3 - Trong bước này, vị trí của các trung tâm mới sẽ được cập nhật.
Step4 - Bây giờ, quá trình sẽ được lặp lại và chuyển đến vùng mật độ cao hơn.
Step5 - Cuối cùng, nó sẽ bị dừng lại khi các trọng tâm đạt đến vị trí mà nó không thể di chuyển xa hơn.
Triển khai bằng Python
Đó là một ví dụ đơn giản để hiểu cách hoạt động của thuật toán Mean-Shift. Trong ví dụ này, trước tiên chúng ta sẽ tạo tập dữ liệu 2D chứa 4 đốm màu khác nhau và sau đó sẽ áp dụng thuật toán Mean-Shift để xem kết quả.
%matplotlib inline
import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.datasets.samples_generator import make_blobs
centers = [[3,3,3],[4,5,5],[3,10,10]]
X, _ = make_blobs(n_samples = 700, centers = centers, cluster_std = 0.5)
plt.scatter(X[:,0],X[:,1])
plt.show()
ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
colors = 10*['r.','g.','b.','c.','k.','y.','m.']
for i in range(len(X)):
plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 3)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
marker=".",color='k', s=20, linewidths = 5, zorder=10)
plt.show()Đầu ra
[[ 2.98462798 9.9733794 10.02629344]
[ 3.94758484 4.99122771 4.99349433]
[ 3.00788996 3.03851268 2.99183033]]
Estimated clusters: 3
Ưu điểm và nhược điểm
Ưu điểm
Sau đây là một số ưu điểm của thuật toán phân cụm Mean-Shift:
Nó không cần phải đưa ra bất kỳ giả định mô hình nào giống như trong hỗn hợp K-mean hoặc Gaussian.
Nó cũng có thể mô hình hóa các cụm phức tạp có hình dạng không lồi.
Nó chỉ cần một tham số có tên là băng thông sẽ tự động xác định số lượng cụm.
Không có vấn đề về cực tiểu cục bộ như trong K-means.
Không có vấn đề nào được tạo ra từ các ngoại lệ.
Nhược điểm
Sau đây là một số nhược điểm của thuật toán phân cụm Mean-Shift:
Thuật toán dịch chuyển trung bình không hoạt động tốt trong trường hợp thứ nguyên cao, trong đó số lượng cụm thay đổi đột ngột.
Chúng tôi không có bất kỳ quyền kiểm soát trực tiếp nào về số lượng cụm nhưng trong một số ứng dụng, chúng tôi cần một số cụm cụ thể.
Nó không thể phân biệt giữa các chế độ có ý nghĩa và vô nghĩa.
Giới thiệu về phân cụm phân cấp
Phân cụm phân cấp là một thuật toán học tập không giám sát khác được sử dụng để nhóm các điểm dữ liệu không được gắn nhãn có các đặc điểm tương tự lại với nhau. Các thuật toán phân cụm phân cấp thuộc hai loại sau:
Agglomerative hierarchical algorithms- Trong các thuật toán phân cấp tích tụ, mỗi điểm dữ liệu được coi như một cụm duy nhất và sau đó hợp nhất hoặc kết tụ liên tiếp (phương pháp tiếp cận từ dưới lên) các cặp cụm. Thứ bậc của các cụm được biểu diễn dưới dạng biểu đồ dendrogram hoặc cấu trúc cây.
Divisive hierarchical algorithms - Mặt khác, trong các thuật toán phân cấp, tất cả các điểm dữ liệu được coi như một cụm lớn và quá trình phân cụm bao gồm việc phân chia (cách tiếp cận từ trên xuống) một cụm lớn thành các cụm nhỏ khác nhau.
Các bước để thực hiện phân cụm phân cấp tổng hợp
Chúng tôi sẽ giải thích cụm từ phân cấp được sử dụng nhiều nhất và quan trọng nhất tức là kết tụ. Các bước thực hiện tương tự như sau:
Step1- Coi mỗi điểm dữ liệu là một cụm duy nhất. Do đó, chúng ta sẽ có K cụm ở đầu. Số điểm dữ liệu cũng sẽ là K khi bắt đầu.
Step2- Bây giờ, trong bước này, chúng ta cần tạo thành một cụm lớn bằng cách nối hai điểm dữ liệu của tủ quần áo. Điều này sẽ dẫn đến tổng số các cụm K-1.
Step3- Bây giờ, để tạo thành nhiều cụm hơn, chúng ta cần nối hai cụm tủ quần áo. Điều này sẽ dẫn đến tổng số K-2 cụm.
Step4 - Bây giờ, để tạo thành một cụm lớn lặp lại ba bước trên cho đến khi K trở thành 0 tức là không còn điểm dữ liệu nào để tham gia.
Step5 - Cuối cùng, sau khi tạo một cụm lớn duy nhất, dendrograms sẽ được sử dụng để chia thành nhiều cụm tùy theo vấn đề.
Vai trò của Dendrograms trong phân cụm phân cấp tổng hợp
Như chúng ta đã thảo luận ở bước cuối cùng, vai trò của dendrogram bắt đầu khi cụm lớn được hình thành. Dendrogram sẽ được sử dụng để chia các cụm thành nhiều cụm điểm dữ liệu liên quan tùy thuộc vào vấn đề của chúng ta. Nó có thể được hiểu với sự trợ giúp của ví dụ sau:
Ví dụ 1
Để hiểu, chúng ta hãy bắt đầu với việc nhập các thư viện bắt buộc như sau:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as npTiếp theo, chúng tôi sẽ vẽ các điểm dữ liệu mà chúng tôi đã lấy cho ví dụ này -
X = np.array([[7,8],[12,20],[17,19],[26,15],[32,37],[87,75],[73,85], [62,80],[73,60],[87,96],])
labels = range(1, 11)
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[:,0],X[:,1], label='True Position')
for label, x, y in zip(labels, X[:, 0], X[:, 1]):
plt.annotate(label,xy=(x, y), xytext=(-3, 3),textcoords='offset points', ha='right', va='bottom')
plt.show()
Từ sơ đồ trên, chúng ta rất dễ thấy rằng chúng ta có hai cụm trong các điểm dữ liệu nhưng trong dữ liệu thế giới thực, có thể có hàng nghìn cụm. Tiếp theo, chúng tôi sẽ vẽ biểu đồ hình ảnh của các điểm dữ liệu của chúng tôi bằng cách sử dụng thư viện Scipy -
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
linked = linkage(X, 'single')
labelList = range(1, 11)
plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top',labels=labelList, distance_sort='descending',show_leaf_counts=True)
plt.show()
Bây giờ, khi cụm lớn được hình thành, khoảng cách dọc dài nhất được chọn. Một đường thẳng đứng sau đó được vẽ qua nó như thể hiện trong sơ đồ sau. Khi đường ngang cắt đường màu xanh lam tại hai điểm, số cụm sẽ là hai.

Tiếp theo, chúng ta cần nhập lớp để phân cụm và gọi phương thức fit_p Dự đoán của nó để dự đoán cụm. Chúng tôi đang nhập lớp AgglomerativeClustering của thư viện sklearn.cluster -
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(X)Tiếp theo, vẽ sơ đồ cụm với sự trợ giúp của mã sau:
plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow')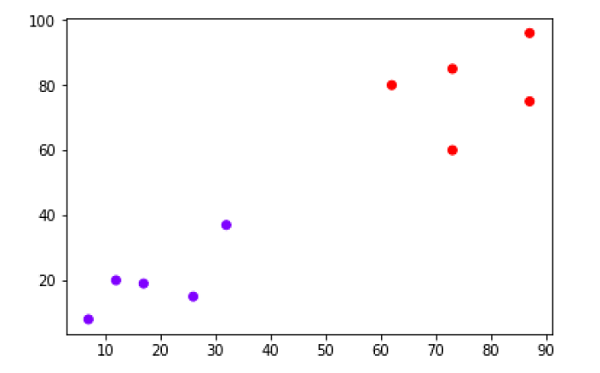
Sơ đồ trên cho thấy hai cụm từ điểm dữ liệu của chúng tôi.
Ví dụ2
Như chúng ta đã hiểu khái niệm về biểu đồ từ ví dụ đơn giản được thảo luận ở trên, chúng ta hãy chuyển sang một ví dụ khác, trong đó chúng ta đang tạo các cụm điểm dữ liệu trong Tập dữ liệu bệnh tiểu đường ở Ấn Độ Pima bằng cách sử dụng phân nhóm phân cấp -
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
import numpy as np
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
data.shape
(768, 9)
data.head()| SI. Không. | mang thai | Plas | Pres | da | kiểm tra | khối lượng | pedi | tuổi tác | lớp học |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33,6 | 0,627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26,6 | 0,351 | 31 | 0 |
| 2 | số 8 | 183 | 64 | 0 | 0 | 23.3 | 0,672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0,167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
patient_data = data.iloc[:, 3:5].values
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Patient Dendograms")
dend = shc.dendrogram(shc.linkage(data, method='ward'))
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
cluster.fit_predict(patient_data)
plt.figure(figsize=(10, 7))
plt.scatter(patient_data[:,0], patient_data[:,1], c=cluster.labels_, cmap='rainbow')
Giới thiệu
Thuật toán K-láng giềng gần nhất (KNN) là một loại thuật toán ML có giám sát có thể được sử dụng cho cả phân loại cũng như các bài toán dự đoán hồi quy. Tuy nhiên, nó chủ yếu được sử dụng để phân loại các vấn đề dự đoán trong công nghiệp. Hai thuộc tính sau đây sẽ xác định tốt KNN:
Lazy learning algorithm - KNN là một thuật toán lười học vì nó không có giai đoạn huấn luyện chuyên biệt và sử dụng tất cả dữ liệu để huấn luyện trong khi phân loại.
Non-parametric learning algorithm - KNN cũng là một thuật toán học phi tham số vì nó không giả định bất cứ điều gì về dữ liệu bên dưới.
Hoạt động của thuật toán KNN
Thuật toán K-láng giềng gần nhất (KNN) sử dụng 'tính năng tương tự' để dự đoán giá trị của điểm dữ liệu mới, điều này có nghĩa là điểm dữ liệu mới sẽ được chỉ định một giá trị dựa trên mức độ phù hợp chặt chẽ của nó với các điểm trong tập huấn luyện. Chúng tôi có thể hiểu cách hoạt động của nó với sự trợ giúp của các bước sau:
Step1- Để thực hiện bất kỳ thuật toán nào, chúng ta cần tập dữ liệu. Vì vậy trong bước đầu tiên của KNN, chúng ta phải tải dữ liệu huấn luyện cũng như kiểm tra.
Step2- Tiếp theo, chúng ta cần chọn giá trị của K tức là các điểm dữ liệu gần nhất. K có thể là bất kỳ số nguyên nào.
Step3 - Đối với mỗi điểm trong dữ liệu kiểm tra, hãy làm như sau:
3.1- Tính toán khoảng cách giữa dữ liệu kiểm tra và mỗi hàng dữ liệu đào tạo với sự trợ giúp của bất kỳ phương pháp nào cụ thể là: Khoảng cách Euclidean, Manhattan hoặc Hamming. Phương pháp phổ biến nhất được sử dụng để tính khoảng cách là Euclidean.
3.2 - Bây giờ, dựa trên giá trị khoảng cách, hãy sắp xếp chúng theo thứ tự tăng dần.
3.3 - Tiếp theo, nó sẽ chọn K hàng trên cùng từ mảng đã sắp xếp.
3.4 - Bây giờ, nó sẽ chỉ định một lớp cho điểm kiểm tra dựa trên lớp thường xuyên nhất của các hàng này.
Step4 - Kết thúc
Thí dụ
Sau đây là một ví dụ để hiểu khái niệm K và hoạt động của thuật toán KNN:
Giả sử chúng ta có một tập dữ liệu có thể được vẽ như sau:
Bây giờ, chúng ta cần phân loại điểm dữ liệu mới với chấm đen (tại điểm 60,60) thành lớp màu xanh lam hoặc màu đỏ. Chúng tôi giả sử K = 3 tức là nó sẽ tìm thấy ba điểm dữ liệu gần nhất. Nó được hiển thị trong sơ đồ tiếp theo -

Chúng ta có thể thấy trong biểu đồ trên ba láng giềng gần nhất của điểm dữ liệu với chấm đen. Trong số ba người đó, hai trong số chúng nằm trong lớp Đỏ do đó chấm đen cũng sẽ được gán trong lớp đỏ.
Triển khai bằng Python
Như chúng ta đã biết, thuật toán K-láng giềng gần nhất (KNN) có thể được sử dụng cho cả phân loại cũng như hồi quy. Sau đây là các công thức trong Python để sử dụng KNN làm bộ phân loại cũng như bộ hồi quy:
KNN làm Bộ phân loại
Đầu tiên, hãy bắt đầu với việc nhập các gói python cần thiết -
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdTiếp theo, tải xuống tập dữ liệu mống mắt từ liên kết web của nó như sau:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Tiếp theo, chúng ta cần gán tên cột cho tập dữ liệu như sau:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Bây giờ, chúng ta cần đọc tập dữ liệu thành khung dữ liệu gấu trúc như sau:
dataset = pd.read_csv(path, names=headernames)
dataset.head()| SI. Không. | lá đài dài | chiều rộng đài hoa | chiều dài cánh hoa | chiều rộng cánh hoa | Lớp học |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1,4 | 0,2 | Iris-setosa |
| 1 | 4,9 | 3.0 | 1,4 | 0,2 | Iris-setosa |
| 2 | 4,7 | 3.2 | 1,3 | 0,2 | Iris-setosa |
| 3 | 4,6 | 3.1 | 1,5 | 0,2 | Iris-setosa |
| 4 | 5.0 | 3.6 | 1,4 | 0,2 | Iris-setosa |
Quá trình tiền xử lý dữ liệu sẽ được thực hiện với sự trợ giúp của các dòng tập lệnh sau:
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].valuesTiếp theo, chúng tôi sẽ chia dữ liệu thành phân chia huấn luyện và thử nghiệm. Đoạn mã sau sẽ chia tập dữ liệu thành 60% dữ liệu đào tạo và 40% dữ liệu kiểm tra -
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40)Tiếp theo, việc chia tỷ lệ dữ liệu sẽ được thực hiện như sau:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Tiếp theo, đào tạo mô hình với sự trợ giúp của lớp KNeighborsClassifier của sklearn như sau:
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=8)
classifier.fit(X_train, y_train)Cuối cùng, chúng ta cần phải dự đoán. Nó có thể được thực hiện với sự trợ giúp của tập lệnh sau:
y_pred = classifier.predict(X_test)Tiếp theo, in kết quả như sau:
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Đầu ra
Confusion Matrix:
[[21 0 0]
[ 0 16 0]
[ 0 7 16]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 21
Iris-versicolor 0.70 1.00 0.82 16
Iris-virginica 1.00 0.70 0.82 23
micro avg 0.88 0.88 0.88 60
macro avg 0.90 0.90 0.88 60
weighted avg 0.92 0.88 0.88 60
Accuracy: 0.8833333333333333KNN làm Regressor
Đầu tiên, hãy bắt đầu với việc nhập các gói Python cần thiết -
import numpy as np
import pandas as pdTiếp theo, tải xuống tập dữ liệu mống mắt từ liên kết web của nó như sau:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Tiếp theo, chúng ta cần gán tên cột cho tập dữ liệu như sau:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Bây giờ, chúng ta cần đọc tập dữ liệu thành khung dữ liệu gấu trúc như sau:
data = pd.read_csv(url, names=headernames)
array = data.values
X = array[:,:2]
Y = array[:,2]
data.shape
output:(150, 5)Tiếp theo, nhập KNeighborsRegressor từ sklearn để phù hợp với mô hình -
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=10)
knnr.fit(X, y)Cuối cùng, chúng ta có thể tìm thấy MSE như sau:
print ("The MSE is:",format(np.power(y-knnr.predict(X),2).mean()))Đầu ra
The MSE is: 0.12226666666666669Ưu nhược điểm của KNN
Ưu điểm
Nó là một thuật toán rất đơn giản để hiểu và giải thích.
Nó rất hữu ích cho dữ liệu phi tuyến vì không có giả định về dữ liệu trong thuật toán này.
Nó là một thuật toán linh hoạt vì chúng ta có thể sử dụng nó để phân loại cũng như hồi quy.
Nó có độ chính xác tương đối cao nhưng có nhiều mô hình học có giám sát tốt hơn KNN.
Nhược điểm
Về mặt tính toán, nó là một thuật toán hơi tốn kém vì nó lưu trữ tất cả các dữ liệu huấn luyện.
Yêu cầu bộ nhớ lưu trữ cao so với các thuật toán học có giám sát khác.
Dự đoán chậm trong trường hợp N lớn.
Nó rất nhạy cảm với quy mô dữ liệu cũng như các tính năng không liên quan.
Các ứng dụng của KNN
Sau đây là một số lĩnh vực mà KNN có thể được áp dụng thành công -
Hệ thống ngân hàng
KNN có thể được sử dụng trong hệ thống ngân hàng để dự đoán thời tiết một cá nhân có phù hợp để phê duyệt khoản vay không? Cá nhân đó có các đặc điểm giống với cá nhân mặc định không?
Tính toán xếp hạng tín dụng
Các thuật toán KNN có thể được sử dụng để tìm xếp hạng tín dụng của một cá nhân bằng cách so sánh với những người có đặc điểm tương tự.
Chính trị
Với sự trợ giúp của các thuật toán KNN, chúng tôi có thể phân loại một cử tri tiềm năng thành nhiều lớp khác nhau như “Sẽ bỏ phiếu”, “Sẽ không bỏ phiếu”, “Sẽ bỏ phiếu cho Đảng 'Đại hội',“ Sẽ bỏ phiếu cho Đảng 'BJP'.
Các lĩnh vực khác mà thuật toán KNN có thể được sử dụng là Nhận dạng giọng nói, Phát hiện chữ viết tay, Nhận dạng hình ảnh và Nhận dạng video.
Có nhiều số liệu khác nhau mà chúng ta có thể sử dụng để đánh giá hiệu suất của các thuật toán ML, phân loại cũng như các thuật toán hồi quy. Chúng tôi phải cẩn thận lựa chọn các số liệu để đánh giá hiệu suất ML bởi vì -
Hiệu suất của các thuật toán ML được đo lường và so sánh như thế nào sẽ hoàn toàn phụ thuộc vào số liệu bạn chọn.
Cách bạn xác định tầm quan trọng của các đặc điểm khác nhau trong kết quả sẽ bị ảnh hưởng hoàn toàn bởi số liệu bạn chọn.
Chỉ số hiệu suất cho các vấn đề phân loại
Chúng ta đã thảo luận về phân loại và các thuật toán của nó trong các chương trước. Ở đây, chúng ta sẽ thảo luận về các số liệu hiệu suất khác nhau có thể được sử dụng để đánh giá các dự đoán cho các vấn đề phân loại.
Ma trận hỗn loạn
Đây là cách dễ nhất để đo lường hiệu suất của một bài toán phân loại trong đó kết quả đầu ra có thể là hai hoặc nhiều loại lớp. Ma trận nhầm lẫn không là gì ngoài một bảng có hai chiều viz. “Thực tế” và “Dự đoán” và hơn nữa, cả hai thứ nguyên đều có “Khẳng định thật (TP)”, “Phủ định thật (TN)”, “Khẳng định sai (FP)”, “Phủ định giả (FN)” như được hiển thị bên dưới -

Giải thích các thuật ngữ liên quan đến ma trận nhầm lẫn như sau:
True Positives (TP) - Đó là trường hợp khi cả lớp thực tế và lớp dự đoán của điểm dữ liệu là 1.
True Negatives (TN) - Đó là trường hợp khi cả lớp thực tế và lớp dự đoán của điểm dữ liệu là 0.
False Positives (FP) - Trường hợp lớp điểm dữ liệu thực tế là 0 và lớp điểm dữ liệu dự đoán là 1.
False Negatives (FN) - Trường hợp lớp điểm dữ liệu thực tế là 1 & lớp điểm dữ liệu dự đoán là 0.
Chúng ta có thể sử dụng hàm repeat_matrix của sklearn.metrics để tính toán Ma trận nhầm lẫn của mô hình phân loại của chúng ta.
Độ chính xác của phân loại
Đây là thước đo hiệu suất phổ biến nhất cho các thuật toán phân loại. Nó có thể được định nghĩa là số dự đoán đúng được thực hiện theo tỷ lệ của tất cả các dự đoán được thực hiện. Chúng ta có thể dễ dàng tính toán nó bằng ma trận nhầm lẫn với sự trợ giúp của công thức sau:
$Accuracy =\frac{TP+TN}{+++}$Chúng tôi có thể sử dụng hàm precision_score của sklearn.metrics để tính độ chính xác của mô hình phân loại của chúng tôi.
Báo cáo phân loại
Báo cáo này bao gồm điểm số của Precision, Recall, F1 và Support. Chúng được giải thích như sau:
Độ chính xác
Độ chính xác, được sử dụng trong truy xuất tài liệu, có thể được định nghĩa là số lượng tài liệu chính xác được trả về bởi mô hình ML của chúng tôi. Chúng ta có thể dễ dàng tính toán nó bằng ma trận nhầm lẫn với sự trợ giúp của công thức sau:
$Precision=\frac{TP}{TP+FP}$Nhớ lại hoặc độ nhạy
Thu hồi có thể được định nghĩa là số lượng dương tính được trả về bởi mô hình ML của chúng tôi. Chúng ta có thể dễ dàng tính toán nó bằng ma trận nhầm lẫn với sự trợ giúp của công thức sau:
$Recall =\frac{TP}{TP+FN}$Tính đặc hiệu
Tính cụ thể, trái ngược với thu hồi, có thể được định nghĩa là số lượng các phủ định được trả về bởi mô hình ML của chúng tôi. Chúng ta có thể dễ dàng tính toán nó bằng ma trận nhầm lẫn với sự trợ giúp của công thức sau:
$Specificity =\frac{TN}{TN+FP}$Ủng hộ
Hỗ trợ có thể được định nghĩa là số lượng mẫu của phản hồi thực sự nằm trong mỗi loại giá trị đích.
Điểm F1
Điểm số này sẽ cung cấp cho chúng ta giá trị trung bình hài hòa của độ chính xác và thu hồi. Về mặt toán học, điểm F1 là trung bình có trọng số của độ chính xác và thu hồi. Giá trị tốt nhất của F1 sẽ là 1 và xấu nhất sẽ là 0. Chúng ta có thể tính điểm F1 với sự trợ giúp của công thức sau:
= ∗ (∗) / (+)
Điểm F1 có đóng góp tương đối ngang nhau về độ chính xác và thu hồi.
Chúng ta có thể sử dụng hàm phân loại của sklearn.metrics để lấy báo cáo phân loại của mô hình phân loại của chúng ta.
AUC (Diện tích dưới đường cong ROC)
AUC (Vùng dưới đường cong) -ROC (Đặc tính hoạt động của máy thu) là một thước đo hiệu suất, dựa trên các giá trị ngưỡng khác nhau, cho các vấn đề phân loại. Như tên cho thấy, ROC là một đường cong xác suất và AUC đo lường khả năng phân tách. Nói một cách dễ hiểu, số liệu AUC-ROC sẽ cho chúng ta biết về khả năng của mô hình trong việc phân biệt các lớp. AUC cao hơn, mô hình tốt hơn.
Về mặt toán học, nó có thể được tạo ra bằng cách vẽ biểu đồ TPR (Tỷ lệ dương tính thực) tức là Độ nhạy hoặc thu hồi so với FPR (Tỷ lệ dương tính giả) tức là Độ đặc hiệu 1, ở các giá trị ngưỡng khác nhau. Sau đây là biểu đồ cho thấy ROC, AUC có TPR tại trục y và FPR tại trục x -

Chúng ta có thể sử dụng hàm roc_auc_score của sklearn.metrics để tính AUC-ROC.
LOGLOSS (Mất Logarit)
Nó còn được gọi là mất mát hồi quy Logistic hoặc mất mát entropy chéo. Về cơ bản, nó được định nghĩa dựa trên các ước tính xác suất và đo lường hiệu suất của một mô hình phân loại trong đó đầu vào là giá trị xác suất từ 0 đến 1. Có thể hiểu rõ hơn bằng cách phân biệt nó với độ chính xác. Như chúng ta biết rằng độ chính xác là số lượng các dự đoán (giá trị dự đoán = giá trị thực tế) trong mô hình của chúng tôi trong khi Log Loss là lượng dự đoán không chắc chắn của chúng tôi dựa trên mức độ thay đổi của nó so với nhãn thực tế. Với sự trợ giúp của giá trị Log Loss, chúng ta có thể có cái nhìn chính xác hơn về hiệu suất của mô hình của mình. Chúng ta có thể sử dụng hàm log_loss của sklearn.metrics để tính toán Log Loss.
Thí dụ
Sau đây là một công thức đơn giản bằng Python sẽ cung cấp cho chúng ta cái nhìn sâu sắc về cách chúng ta có thể sử dụng các số liệu hiệu suất được giải thích ở trên trên mô hình phân loại nhị phân -
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
from sklearn.metrics import log_loss
X_actual = [1, 1, 0, 1, 0, 0, 1, 0, 0, 0]
Y_predic = [1, 0, 1, 1, 1, 0, 1, 1, 0, 0]
results = confusion_matrix(X_actual, Y_predic)
print ('Confusion Matrix :')
print(results)
print ('Accuracy Score is',accuracy_score(X_actual, Y_predic))
print ('Classification Report : ')
print (classification_report(X_actual, Y_predic))
print('AUC-ROC:',roc_auc_score(X_actual, Y_predic))
print('LOGLOSS Value is',log_loss(X_actual, Y_predic))Đầu ra
Confusion Matrix :
[[3 3]
[1 3]]
Accuracy Score is 0.6
Classification Report :
precision recall f1-score support
0 0.75 0.50 0.60 6
1 0.50 0.75 0.60 4
micro avg 0.60 0.60 0.60 10
macro avg 0.62 0.62 0.60 10
weighted avg 0.65 0.60 0.60 10
AUC-ROC: 0.625
LOGLOSS Value is 13.815750437193334Chỉ số hiệu suất cho các vấn đề hồi quy
Chúng ta đã thảo luận về hồi quy và các thuật toán của nó trong các chương trước. Ở đây, chúng ta sẽ thảo luận về các số liệu hiệu suất khác nhau có thể được sử dụng để đánh giá các dự đoán cho các vấn đề hồi quy.
Lỗi tuyệt đối trung bình (MAE)
Đây là số liệu lỗi đơn giản nhất được sử dụng trong các bài toán hồi quy. Về cơ bản, nó là tổng giá trị trung bình của sự khác biệt tuyệt đối giữa giá trị dự đoán và giá trị thực tế. Nói một cách dễ hiểu, với MAE, chúng ta có thể biết được mức độ sai của các dự đoán. MAE không chỉ ra hướng của mô hình tức là không có dấu hiệu nào về hoạt động kém hiệu quả hoặc hoạt động quá mức của mô hình. Sau đây là công thức tính MAE:
$MAE = \frac{1}{n}\sum|Y -\hat{Y}|$Đây, = Giá trị đầu ra thực tế
Và $\hat{Y}$= Giá trị đầu ra dự đoán.
Chúng ta có thể sử dụng hàm mean_absolute_error của sklearn.metrics để tính MAE.
Lỗi hình vuông trung bình (MSE)
MSE giống như MAE, nhưng sự khác biệt duy nhất là nó bình phương sự khác biệt của các giá trị đầu ra thực tế và dự đoán trước khi tổng hợp tất cả chúng thay vì sử dụng giá trị tuyệt đối. Có thể nhận thấy sự khác biệt trong phương trình sau:
$MSE = \frac{1}{n}\sum(Y -\hat{Y})$Đây, = Giá trị đầu ra thực tế
Và $\hat{Y}$ = Giá trị đầu ra dự đoán.
Chúng ta có thể sử dụng hàm mean_squared_error của sklearn.metrics để tính MSE.
R Bình phương (R 2 )
R Chỉ số bình phương thường được sử dụng cho mục đích giải thích và cung cấp chỉ báo về mức độ tốt hoặc phù hợp của một tập hợp các giá trị đầu ra dự đoán với các giá trị đầu ra thực tế. Công thức sau đây sẽ giúp chúng ta hiểu nó:
$R^{2} = 1 -\frac{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\hat{Y_{i}})^2}{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\bar{Y_i)^2}}$Trong phương trình trên, tử số là MSE và mẫu số là phương sai của các giá trị.
Chúng ta có thể sử dụng hàm r2_score của sklearn.metrics để tính giá trị bình phương R.
Thí dụ
Sau đây là một công thức đơn giản bằng Python sẽ cho chúng ta cái nhìn sâu sắc về cách chúng ta có thể sử dụng các số liệu hiệu suất được giải thích ở trên trên mô hình hồi quy -
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
X_actual = [5, -1, 2, 10]
Y_predic = [3.5, -0.9, 2, 9.9]
print ('R Squared =',r2_score(X_actual, Y_predic))
print ('MAE =',mean_absolute_error(X_actual, Y_predic))
print ('MSE =',mean_squared_error(X_actual, Y_predic))Đầu ra
R Squared = 0.9656060606060606
MAE = 0.42499999999999993
MSE = 0.5674999999999999Giới thiệu
Để thực thi và tạo ra kết quả thành công, một mô hình học máy phải tự động hóa một số quy trình công việc tiêu chuẩn. Quá trình tự động hóa các quy trình công việc tiêu chuẩn này có thể được thực hiện với sự trợ giúp của Scikit-learning Pipelines. Từ quan điểm của nhà khoa học dữ liệu, đường ống là một khái niệm tổng quát, nhưng rất quan trọng. Về cơ bản, nó cho phép luồng dữ liệu từ định dạng thô của nó đến một số thông tin hữu ích. Hoạt động của đường ống có thể được hiểu với sự trợ giúp của sơ đồ sau:

Các khối của đường ống ML như sau:
Data ingestion- Như tên cho thấy, nó là quá trình nhập dữ liệu để sử dụng trong dự án ML. Dữ liệu có thể được trích xuất trong thời gian thực hoặc theo lô từ một hoặc nhiều hệ thống. Đây là một trong những bước thử thách nhất vì chất lượng dữ liệu có thể ảnh hưởng đến toàn bộ mô hình ML.
Data Preparation- Sau khi nhập dữ liệu, chúng ta cần chuẩn bị dữ liệu để sử dụng cho mô hình ML của mình. Tiền xử lý dữ liệu là một trong những kỹ thuật chuẩn bị dữ liệu quan trọng nhất.
ML Model Training- Bước tiếp theo là đào tạo mô hình ML của chúng tôi. Chúng tôi có các thuật toán ML khác nhau như có giám sát, không giám sát, tăng cường để trích xuất các tính năng từ dữ liệu và đưa ra dự đoán.
Model Evaluation- Tiếp theo, chúng ta cần đánh giá mô hình ML. Trong trường hợp đường ống AutoML, mô hình ML có thể được đánh giá với sự trợ giúp của các phương pháp thống kê và quy tắc nghiệp vụ khác nhau.
ML Model retraining- Trong trường hợp đường ống AutoML, không nhất thiết mô hình đầu tiên là tốt nhất. Mô hình đầu tiên được coi là mô hình cơ sở và chúng tôi có thể đào tạo lặp lại mô hình đó để tăng độ chính xác của mô hình.
Deployment- Cuối cùng, chúng ta cần triển khai mô hình. Bước này liên quan đến việc áp dụng và chuyển mô hình sang hoạt động kinh doanh để sử dụng.
Những thách thức đi kèm với đường ống ML
Để tạo ra đường ống ML, các nhà khoa học dữ liệu phải đối mặt với nhiều thách thức. Những thách thức này thuộc ba loại sau:
Chất lượng dữ liệu
Sự thành công của bất kỳ mô hình ML nào phụ thuộc nhiều vào chất lượng dữ liệu. Nếu dữ liệu chúng tôi cung cấp cho mô hình ML không chính xác, đáng tin cậy và mạnh mẽ, thì chúng tôi sẽ kết thúc với kết quả sai hoặc gây hiểu nhầm.
Độ tin cậy của dữ liệu
Một thách thức khác liên quan đến đường ống ML là độ tin cậy của dữ liệu chúng tôi đang cung cấp cho mô hình ML. Như chúng ta biết, có thể có nhiều nguồn khác nhau mà từ đó nhà khoa học dữ liệu có thể thu thập dữ liệu nhưng để có được kết quả tốt nhất, phải đảm bảo rằng nguồn dữ liệu đó là đáng tin cậy và đáng tin cậy.
Khả năng tiếp cận dữ liệu
Để có được kết quả tốt nhất từ các đường ống ML, bản thân dữ liệu phải có thể truy cập được, đòi hỏi phải hợp nhất, làm sạch và quản lý dữ liệu. Do thuộc tính trợ năng dữ liệu, siêu dữ liệu sẽ được cập nhật bằng các thẻ mới.
Lập mô hình đường ống ML và chuẩn bị dữ liệu
Rò rỉ dữ liệu, xảy ra từ tập dữ liệu đào tạo đến tập dữ liệu kiểm tra, là một vấn đề quan trọng đối với nhà khoa học dữ liệu trong khi chuẩn bị dữ liệu cho mô hình ML. Nói chung, tại thời điểm chuẩn bị dữ liệu, nhà khoa học dữ liệu sử dụng các kỹ thuật như chuẩn hóa hoặc chuẩn hóa trên toàn bộ tập dữ liệu trước khi học. Nhưng những kỹ thuật này không thể giúp chúng ta khỏi việc rò rỉ dữ liệu vì tập dữ liệu huấn luyện sẽ bị ảnh hưởng bởi quy mô của dữ liệu trong tập dữ liệu thử nghiệm.
Bằng cách sử dụng các đường ống ML, chúng tôi có thể ngăn chặn sự rò rỉ dữ liệu này vì các đường ống dẫn đảm bảo rằng việc chuẩn bị dữ liệu như chuẩn hóa bị hạn chế trong từng phần của quy trình xác thực chéo của chúng tôi.
Thí dụ
Sau đây là một ví dụ bằng Python chứng minh quy trình chuẩn bị dữ liệu và đánh giá mô hình. Vì mục đích này, chúng tôi đang sử dụng bộ dữ liệu về bệnh tiểu đường ở Ấn Độ Pima từ Sklearn. Đầu tiên, chúng tôi sẽ tạo đường dẫn chuẩn hóa dữ liệu. Sau đó, một mô hình phân tích Phân biệt Tuyến tính sẽ được tạo và cuối cùng đường ống sẽ được đánh giá bằng cách sử dụng xác nhận chéo 10 lần.
Đầu tiên, nhập các gói được yêu cầu như sau:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.discriminant_analysis import LinearDiscriminantAnalysisBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.valuesTiếp theo, chúng ta sẽ tạo một đường dẫn với sự trợ giúp của đoạn mã sau:
estimators = []
estimators.append(('standardize', StandardScaler()))
estimators.append(('lda', LinearDiscriminantAnalysis()))
model = Pipeline(estimators)Cuối cùng, chúng tôi sẽ đánh giá đường ống này và đưa ra độ chính xác của nó như sau:
kfold = KFold(n_splits=20, random_state=7)
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Đầu ra
0.7790148448043184Kết quả trên là tóm tắt về độ chính xác của thiết lập trên tập dữ liệu.
Mô hình hóa đường ống ML và trích xuất tính năng
Rò rỉ dữ liệu cũng có thể xảy ra ở bước trích xuất tính năng của mô hình ML. Đó là lý do tại sao các quy trình trích xuất tính năng cũng nên được hạn chế để ngăn chặn rò rỉ dữ liệu trong tập dữ liệu đào tạo của chúng tôi. Như trong trường hợp chuẩn bị dữ liệu, bằng cách sử dụng đường ống ML, chúng tôi cũng có thể ngăn chặn sự rò rỉ dữ liệu này. FeatureUnion, một công cụ được cung cấp bởi các đường ống ML có thể được sử dụng cho mục đích này.
Thí dụ
Sau đây là một ví dụ bằng Python trình bày quy trình khai thác tính năng và đánh giá mô hình. Vì mục đích này, chúng tôi đang sử dụng bộ dữ liệu về bệnh tiểu đường ở Ấn Độ Pima từ Sklearn.
Đầu tiên, 3 tính năng sẽ được trích xuất bằng PCA (Phân tích thành phần chính). Sau đó, 6 tính năng sẽ được trích xuất với Phân tích thống kê. Sau khi trích xuất đặc điểm, kết quả của nhiều quy trình lựa chọn và trích xuất đối tượng sẽ được kết hợp bằng cách sử dụng
Công cụ FeatureUnion. Cuối cùng, một mô hình Hồi quy logistic sẽ được tạo và đường ống sẽ được đánh giá bằng cách sử dụng xác thực chéo 10 lần.
Đầu tiên, nhập các gói được yêu cầu như sau:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.pipeline import FeatureUnion
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
from sklearn.feature_selection import SelectKBestBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.valuesTiếp theo, liên hợp tính năng sẽ được tạo như sau:
features = []
features.append(('pca', PCA(n_components=3)))
features.append(('select_best', SelectKBest(k=6)))
feature_union = FeatureUnion(features)Tiếp theo, đường ống sẽ được tạo với sự trợ giúp của các dòng tập lệnh sau:
estimators = []
estimators.append(('feature_union', feature_union))
estimators.append(('logistic', LogisticRegression()))
model = Pipeline(estimators)Cuối cùng, chúng tôi sẽ đánh giá đường ống này và đưa ra độ chính xác của nó như sau:
kfold = KFold(n_splits=20, random_state=7)
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Đầu ra
0.7789811066126855Kết quả trên là tóm tắt về độ chính xác của thiết lập trên tập dữ liệu.
Cải thiện hiệu suất với các bộ phận lắp ráp
Ensembles có thể giúp chúng tôi tăng cường kết quả học máy bằng cách kết hợp một số mô hình. Về cơ bản, các mô hình tổng hợp bao gồm một số mô hình học tập có giám sát được đào tạo riêng lẻ và kết quả của chúng được hợp nhất theo nhiều cách khác nhau để đạt được hiệu suất dự đoán tốt hơn so với một mô hình duy nhất. Phương pháp gộp có thể được chia thành hai nhóm sau:
Các phương pháp tổng hợp tuần tự
Như tên của nó, trong loại phương pháp tổng hợp này, các trình học cơ sở được tạo tuần tự. Động cơ của các phương pháp như vậy là khai thác sự phụ thuộc giữa những người học cơ sở.
Các phương pháp kết hợp song song
Như tên của nó, trong loại phương pháp tổng hợp này, các học viên cơ sở được tạo ra song song. Động cơ của các phương pháp đó là khai thác tính độc lập giữa những người học cơ sở.
Phương pháp học tập kết hợp
Sau đây là các phương pháp học tập tổng hợp phổ biến nhất, tức là các phương pháp kết hợp các dự đoán từ các mô hình khác nhau -
Đóng bao
Thuật ngữ đóng bao còn được gọi là tổng hợp bootstrap. Trong phương pháp đóng bao, mô hình tổng hợp cố gắng cải thiện độ chính xác của dự đoán và giảm phương sai của mô hình bằng cách kết hợp các dự đoán của các mô hình riêng lẻ được đào tạo với các mẫu đào tạo được tạo ngẫu nhiên. Dự đoán cuối cùng của mô hình tổng hợp sẽ được đưa ra bằng cách tính giá trị trung bình của tất cả các dự đoán từ các công cụ ước tính riêng lẻ. Một trong những ví dụ điển hình về phương pháp đóng bao là rừng ngẫu nhiên.
Thúc đẩy
Trong phương pháp thúc đẩy, nguyên tắc chính của việc xây dựng mô hình tổng hợp là xây dựng nó tăng dần bằng cách đào tạo tuần tự từng công cụ ước lượng mô hình cơ sở. Như tên cho thấy, về cơ bản, nó kết hợp những người học cơ bản vài tuần, được đào tạo tuần tự qua nhiều lần lặp lại dữ liệu đào tạo, để tạo ra một nhóm mạnh mẽ. Trong quá trình đào tạo các học viên cơ bản theo tuần, các trọng số cao hơn được chỉ định cho những học viên đã được phân loại sai trước đó. Ví dụ về phương pháp thúc đẩy là AdaBoost.
Biểu quyết
Trong mô hình học tập tổng hợp này, nhiều mô hình thuộc các loại khác nhau được xây dựng và một số thống kê đơn giản, như tính giá trị trung bình hoặc trung vị, v.v., được sử dụng để kết hợp các dự đoán. Dự đoán này sẽ đóng vai trò là đầu vào bổ sung cho quá trình đào tạo để đưa ra dự đoán cuối cùng.
Đóng gói các thuật toán kết hợp
Sau đây là ba thuật toán tổng hợp đóng gói -
Cây quyết định có túi
Như chúng ta biết rằng các phương pháp tổng hợp đóng gói hoạt động tốt với các thuật toán có phương sai cao và trong mối quan tâm này, phương pháp tốt nhất là thuật toán cây quyết định. Trong công thức Python sau đây, chúng ta sẽ xây dựng mô hình tổng hợp cây quyết định có túi bằng cách sử dụng hàm BaggingClassifier của sklearn với Quyết địnhTreeClasifier (một thuật toán phân loại & cây hồi quy) trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima.
Đầu tiên, nhập các gói được yêu cầu như sau:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifierBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như chúng ta đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Tiếp theo, cung cấp đầu vào để xác nhận chéo 10 lần như sau:
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
cart = DecisionTreeClassifier()Chúng tôi cần cung cấp số lượng cây mà chúng tôi sẽ xây dựng. Ở đây chúng tôi đang xây dựng 150 cây xanh -
num_trees = 150Tiếp theo, xây dựng mô hình với sự trợ giúp của tập lệnh sau:
model = BaggingClassifier(base_estimator=cart, n_estimators=num_trees, random_state=seed)Tính toán và in kết quả như sau:
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Đầu ra
0.7733766233766234Kết quả ở trên cho thấy rằng chúng tôi có độ chính xác khoảng 77% của mô hình phân loại cây quyết định được đóng gói.
Rừng ngẫu nhiên
Nó là một phần mở rộng của cây quyết định có túi. Đối với các bộ phân loại riêng lẻ, các mẫu của tập dữ liệu huấn luyện được lấy để thay thế, nhưng các cây được xây dựng theo cách làm giảm mối tương quan giữa chúng. Ngoài ra, một tập hợp con ngẫu nhiên của các tính năng được xem xét để chọn từng điểm tách thay vì tham lam chọn điểm phân tách tốt nhất trong việc xây dựng mỗi cây.
Trong công thức Python sau đây, chúng ta sẽ xây dựng mô hình quần thể rừng ngẫu nhiên có túi bằng cách sử dụng lớp RandomForestClassifier của sklearn trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima.
Đầu tiên, nhập các gói được yêu cầu như sau:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifierBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Tiếp theo, cung cấp đầu vào để xác nhận chéo 10 lần như sau:
seed = 7
kfold = KFold(n_splits=10, random_state=seed)Chúng tôi cần cung cấp số lượng cây mà chúng tôi sẽ xây dựng. Ở đây chúng tôi đang xây dựng 150 cây với các điểm phân tách được chọn từ 5 tính năng -
num_trees = 150
max_features = 5Tiếp theo, xây dựng mô hình với sự trợ giúp của tập lệnh sau:
model = RandomForestClassifier(n_estimators=num_trees, max_features=max_features)Tính toán và in kết quả như sau:
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Đầu ra
0.7629357484620642Kết quả ở trên cho thấy rằng mô hình phân loại rừng ngẫu nhiên có túi của chúng tôi có độ chính xác khoảng 76%.
Cây phụ
Nó là một phần mở rộng khác của phương pháp tập hợp cây quyết định được đóng gói. Trong phương pháp này, các cây ngẫu nhiên được xây dựng từ các mẫu của tập dữ liệu huấn luyện.
Trong công thức Python sau, chúng ta sẽ xây dựng thêm mô hình nhóm cây bằng cách sử dụng lớp ExtraTreesClassifier của sklearn trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima.
Đầu tiên, nhập các gói được yêu cầu như sau:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifierBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Tiếp theo, cung cấp đầu vào để xác nhận chéo 10 lần như sau:
seed = 7
kfold = KFold(n_splits=10, random_state=seed)Chúng tôi cần cung cấp số lượng cây mà chúng tôi sẽ xây dựng. Ở đây chúng tôi đang xây dựng 150 cây với các điểm phân tách được chọn từ 5 tính năng -
num_trees = 150
max_features = 5Tiếp theo, xây dựng mô hình với sự trợ giúp của tập lệnh sau:
model = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)Tính toán và in kết quả như sau:
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Đầu ra
0.7551435406698566Kết quả ở trên cho thấy rằng chúng tôi có độ chính xác khoảng 75,5% của mô hình phân loại cây phụ có túi của chúng tôi.
Thúc đẩy các thuật toán Ensemble
Sau đây là hai thuật toán tổng hợp tăng cường phổ biến nhất -
AdaBoost
Đây là một trong những thuật toán tổng hợp thúc đẩy thành công nhất. Chìa khóa chính của thuật toán này là ở cách chúng đưa ra trọng số cho các thể hiện trong tập dữ liệu. Do đó, thuật toán cần chú ý ít hơn đến các cá thể trong khi xây dựng các mô hình tiếp theo.
Trong công thức Python sau đây, chúng tôi sẽ xây dựng mô hình tổng thể Ada Boost để phân loại bằng cách sử dụng lớp AdaBoostClassifier của sklearn trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima.
Đầu tiên, nhập các gói được yêu cầu như sau:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifierBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Tiếp theo, cung cấp đầu vào để xác nhận chéo 10 lần như sau:
seed = 5
kfold = KFold(n_splits=10, random_state=seed)Chúng tôi cần cung cấp số lượng cây mà chúng tôi sẽ xây dựng. Ở đây chúng tôi đang xây dựng 150 cây với các điểm phân tách được chọn từ 5 tính năng -
num_trees = 50Tiếp theo, xây dựng mô hình với sự trợ giúp của tập lệnh sau:
model = AdaBoostClassifier(n_estimators=num_trees, random_state=seed)Tính toán và in kết quả như sau:
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Đầu ra
0.7539473684210527Kết quả ở trên cho thấy rằng chúng tôi có độ chính xác khoảng 75% của mô hình tổng hợp trình phân loại AdaBoost của mình.
Stochastic Gradient Bo boost
Nó còn được gọi là Máy tăng cường độ dốc. Trong công thức Python sau đây, chúng ta sẽ xây dựng mô hình Stochastic Gradient Boostingensemble để phân loại bằng cách sử dụng lớp GradientBoostingClassifier của sklearn trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima.
Đầu tiên, nhập các gói được yêu cầu như sau:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifierBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Tiếp theo, cung cấp đầu vào để xác nhận chéo 10 lần như sau:
seed = 5
kfold = KFold(n_splits=10, random_state=seed)Chúng tôi cần cung cấp số lượng cây mà chúng tôi sẽ xây dựng. Ở đây chúng tôi đang xây dựng 150 cây với các điểm phân tách được chọn từ 5 tính năng -
num_trees = 50Tiếp theo, xây dựng mô hình với sự trợ giúp của tập lệnh sau:
model = GradientBoostingClassifier(n_estimators=num_trees, random_state=seed)Tính toán và in kết quả như sau:
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Đầu ra
0.7746582365003418Kết quả ở trên cho thấy rằng chúng tôi có độ chính xác khoảng 77,5% của mô hình tổng hợp bộ phân loại Gradient Bo boost.
Bầu chọn thuật toán tập hợp
Như đã thảo luận, việc bỏ phiếu trước tiên sẽ tạo ra hai hoặc nhiều mô hình độc lập từ tập dữ liệu đào tạo và sau đó bộ phân loại biểu quyết sẽ bao bọc mô hình cùng với việc lấy giá trị trung bình của các dự đoán của mô hình con bất cứ khi nào cần dữ liệu mới.
Trong công thức Python sau đây, chúng ta sẽ xây dựng mô hình tổ hợp Bầu cử để phân loại bằng cách sử dụng lớp VotingClassifier của sklearn trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima. Chúng tôi đang kết hợp các dự đoán của hồi quy logistic, bộ phân loại Cây quyết định và SVM với nhau cho một bài toán phân loại như sau:
Đầu tiên, nhập các gói được yêu cầu như sau:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifierBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Tiếp theo, cung cấp đầu vào để xác nhận chéo 10 lần như sau:
kfold = KFold(n_splits=10, random_state=7)Tiếp theo, chúng ta cần tạo các mô hình con như sau:
estimators = []
model1 = LogisticRegression()
estimators.append(('logistic', model1))
model2 = DecisionTreeClassifier()
estimators.append(('cart', model2))
model3 = SVC()
estimators.append(('svm', model3))Bây giờ, hãy tạo mô hình nhóm biểu quyết bằng cách kết hợp các dự đoán của các mô hình phụ đã tạo ở trên.
ensemble = VotingClassifier(estimators)
results = cross_val_score(ensemble, X, Y, cv=kfold)
print(results.mean())Đầu ra
0.7382262474367738Kết quả ở trên cho thấy rằng chúng tôi có độ chính xác khoảng 74% của mô hình tập hợp bộ phân loại biểu quyết của chúng tôi.
Cải thiện hiệu suất với Điều chỉnh thuật toán
Như chúng ta biết rằng các mô hình ML được tham số hóa theo cách mà hành vi của chúng có thể được điều chỉnh cho một vấn đề cụ thể. Điều chỉnh thuật toán có nghĩa là tìm ra sự kết hợp tốt nhất của các tham số này để có thể cải thiện hiệu suất của mô hình ML. Quá trình này đôi khi được gọi là tối ưu hóa siêu tham số và các tham số của chính thuật toán được gọi là siêu tham số và các hệ số được tìm thấy bởi thuật toán ML được gọi là tham số.
Ở đây, chúng ta sẽ thảo luận về một số phương pháp điều chỉnh tham số thuật toán do Python Scikit-learning cung cấp.
Điều chỉnh tham số tìm kiếm lưới
Đó là một cách tiếp cận điều chỉnh tham số. Điểm chính hoạt động của phương pháp này là nó xây dựng và đánh giá mô hình một cách có phương pháp cho mọi kết hợp có thể có của tham số thuật toán được chỉ định trong một lưới. Do đó, chúng ta có thể nói rằng thuật toán này có tính chất tìm kiếm.
Thí dụ
Trong công thức Python sau đây, chúng tôi sẽ thực hiện tìm kiếm lưới bằng cách sử dụng lớp GridSearchCV của sklearn để đánh giá các giá trị alpha khác nhau cho thuật toán hồi quy Ridge trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima.
Đầu tiên, nhập các gói được yêu cầu như sau:
import numpy
from pandas import read_csv
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCVBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Tiếp theo, đánh giá các giá trị alpha khác nhau như sau:
alphas = numpy.array([1,0.1,0.01,0.001,0.0001,0])
param_grid = dict(alpha=alphas)Bây giờ, chúng ta cần áp dụng tìm kiếm lưới trên mô hình của mình -
model = Ridge()
grid = GridSearchCV(estimator=model, param_grid=param_grid)
grid.fit(X, Y)In kết quả với dòng script sau:
print(grid.best_score_)
print(grid.best_estimator_.alpha)Đầu ra
0.2796175593129722
1.0Kết quả trên cho chúng ta điểm tối ưu và tập hợp các tham số trong lưới đạt được điểm đó. Giá trị alpha trong trường hợp này là 1,0.
Điều chỉnh tham số tìm kiếm ngẫu nhiên
Đó là một cách tiếp cận điều chỉnh tham số. Điểm chính hoạt động của phương pháp này là nó lấy mẫu các tham số thuật toán từ một phân phối ngẫu nhiên cho một số lần lặp cố định.
Thí dụ
Trong công thức Python sau, chúng tôi sẽ thực hiện tìm kiếm ngẫu nhiên bằng cách sử dụng lớp RandomizedSearchCV của sklearn để đánh giá các giá trị alpha khác nhau từ 0 đến 1 cho thuật toán hồi quy Ridge trên tập dữ liệu bệnh tiểu đường của người da đỏ Pima.
Đầu tiên, nhập các gói được yêu cầu như sau:
import numpy
from pandas import read_csv
from scipy.stats import uniform
from sklearn.linear_model import Ridge
from sklearn.model_selection import RandomizedSearchCVBây giờ, chúng ta cần tải tập dữ liệu bệnh tiểu đường Pima như đã làm trong các ví dụ trước -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Tiếp theo, đánh giá các giá trị alpha khác nhau trên thuật toán hồi quy Ridge như sau:
param_grid = {'alpha': uniform()}
model = Ridge()
random_search = RandomizedSearchCV(estimator=model, param_distributions=param_grid, n_iter=50,
random_state=7)
random_search.fit(X, Y)In kết quả với dòng script sau:
print(random_search.best_score_)
print(random_search.best_estimator_.alpha)Đầu ra
0.27961712703051084
0.9779895119966027
0.9779895119966027Kết quả trên cho chúng ta điểm tối ưu tương tự như tìm kiếm lưới.