Thuật toán hồi quy - Hồi quy tuyến tính
Giới thiệu về hồi quy tuyến tính
Hồi quy tuyến tính có thể được định nghĩa là mô hình thống kê phân tích mối quan hệ tuyến tính giữa một biến phụ thuộc với một tập hợp các biến độc lập nhất định. Mối quan hệ tuyến tính giữa các biến có nghĩa là khi giá trị của một hoặc nhiều biến độc lập thay đổi (tăng hoặc giảm) thì giá trị của biến phụ thuộc cũng thay đổi theo (tăng hoặc giảm).
Về mặt toán học, mối quan hệ có thể được biểu diễn với sự trợ giúp của phương trình sau:
Y = mX + b
Ở đây, Y là biến phụ thuộc mà chúng tôi đang cố gắng dự đoán
X là biến phụ thuộc mà chúng tôi đang sử dụng để đưa ra dự đoán.
m là độ dốc của đường hồi quy biểu thị ảnh hưởng của X đối với Y
b là một hằng số, được gọi là Y-intercept. Nếu X = 0, Y sẽ bằng b.
Hơn nữa, mối quan hệ tuyến tính có thể là tích cực hoặc tiêu cực về bản chất như được giải thích dưới đây:
Mối quan hệ tuyến tính tích cực
Một mối quan hệ tuyến tính sẽ được gọi là dương nếu cả biến độc lập và biến phụ thuộc đều tăng. Nó có thể được hiểu với sự trợ giúp của đồ thị sau:

Mối quan hệ tuyến tính phủ định
Một mối quan hệ tuyến tính sẽ được gọi là tích cực nếu tăng độc lập và biến phụ thuộc giảm. Nó có thể được hiểu với sự trợ giúp của đồ thị sau:

Các loại hồi quy tuyến tính
Hồi quy tuyến tính có hai loại sau:
- Hồi quy tuyến tính cơ bản
- Hồi quy nhiều tuyến tính
Hồi quy tuyến tính đơn giản (SLR)
Đây là phiên bản cơ bản nhất của hồi quy tuyến tính dự đoán phản hồi bằng cách sử dụng một tính năng duy nhất. Giả định trong SLR là hai biến có liên quan tuyến tính.
Triển khai Python
Chúng ta có thể triển khai SLR bằng Python theo hai cách, một là cung cấp tập dữ liệu của riêng bạn và cách khác là sử dụng tập dữ liệu từ thư viện python scikit-learning.
Example 1 - Trong ví dụ triển khai Python sau đây, chúng tôi đang sử dụng tập dữ liệu của riêng mình.
Đầu tiên, chúng ta sẽ bắt đầu với việc nhập các gói cần thiết như sau:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltTiếp theo, xác định một hàm sẽ tính toán các giá trị quan trọng cho SLR -
def coef_estimation(x, y):Dòng kịch bản sau đây sẽ cung cấp số lượng quan sát n -
n = np.size(x)Giá trị trung bình của vectơ x và y có thể được tính như sau:
m_x, m_y = np.mean(x), np.mean(y)Chúng ta có thể tìm độ lệch chéo và độ lệch về x như sau:
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xTiếp theo, các hệ số hồi quy tức là b có thể được tính như sau:
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)Tiếp theo, chúng ta cần xác định một hàm sẽ vẽ đường hồi quy cũng như sẽ dự đoán vectơ phản hồi -
def plot_regression_line(x, y, b):Dòng kịch bản sau sẽ vẽ các điểm thực tế dưới dạng âm mưu phân tán -
plt.scatter(x, y, color = "m", marker = "o", s = 30)Dòng script sau sẽ dự đoán vectơ phản hồi -
y_pred = b[0] + b[1]*xCác dòng script sau sẽ vẽ dòng hồi quy và sẽ dán nhãn lên chúng -
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()Cuối cùng, chúng ta cần xác định hàm main () để cung cấp tập dữ liệu và gọi hàm mà chúng ta đã xác định ở trên -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()Đầu ra
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788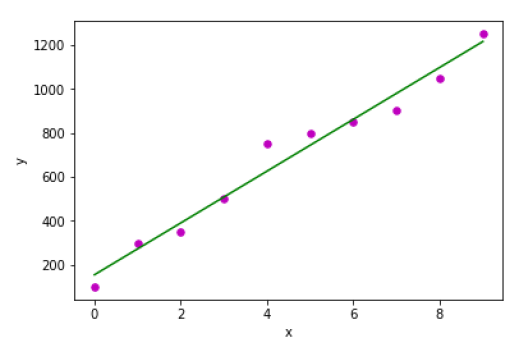
Example 2 - Trong ví dụ triển khai Python sau đây, chúng tôi đang sử dụng tập dữ liệu bệnh tiểu đường từ scikit-learning.
Đầu tiên, chúng ta sẽ bắt đầu với việc nhập các gói cần thiết như sau:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreTiếp theo, chúng tôi sẽ tải tập dữ liệu bệnh tiểu đường và tạo đối tượng của nó -
diabetes = datasets.load_diabetes()Khi chúng tôi đang triển khai SLR, chúng tôi sẽ chỉ sử dụng một tính năng như sau:
X = diabetes.data[:, np.newaxis, 2]Tiếp theo, chúng ta cần chia dữ liệu thành các tập huấn luyện và thử nghiệm như sau:
X_train = X[:-30]
X_test = X[-30:]Tiếp theo, chúng ta cần chia mục tiêu thành các nhóm đào tạo và kiểm tra như sau:
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]Bây giờ, để đào tạo mô hình, chúng ta cần tạo đối tượng hồi quy tuyến tính như sau:
regr = linear_model.LinearRegression()Tiếp theo, huấn luyện mô hình bằng cách sử dụng các tập huấn luyện như sau:
regr.fit(X_train, y_train)Tiếp theo, đưa ra dự đoán bằng cách sử dụng bộ thử nghiệm như sau:
y_pred = regr.predict(X_test)Tiếp theo, chúng tôi sẽ in một số hệ số như MSE, điểm phương sai, v.v. như sau:
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))Bây giờ, vẽ các kết quả đầu ra như sau:
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()Đầu ra
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Hồi quy nhiều tuyến tính (MLR)
Nó là phần mở rộng của hồi quy tuyến tính đơn giản dự đoán một phản hồi bằng cách sử dụng hai hoặc nhiều tính năng. Về mặt toán học, chúng ta có thể giải thích nó như sau:
Xét một tập dữ liệu có n quan sát, p đặc trưng tức là biến độc lập và y là một phản hồi tức là biến phụ thuộc, đường hồi quy cho p đặc trưng có thể được tính như sau:
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} $$Ở đây, h (x i ) là giá trị phản hồi dự đoán và b 0 , b 1 , b 2 …, b p là các hệ số hồi quy.
Nhiều mô hình hồi quy tuyến tính luôn bao gồm các lỗi trong dữ liệu được gọi là lỗi dư, điều này làm thay đổi phép tính như sau:
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} + e_ {i} $$Chúng ta cũng có thể viết phương trình trên như sau:
$$ y_ {i} = h (x_ {i}) + e_ {i} \: hoặc \: e_ {i} = y_ {i} - h (x_ {i}) $$Triển khai Python
trong ví dụ này, chúng tôi sẽ sử dụng tập dữ liệu nhà ở Boston từ scikit learning -
Đầu tiên, chúng ta sẽ bắt đầu với việc nhập các gói cần thiết như sau:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsTiếp theo, tải tập dữ liệu như sau:
boston = datasets.load_boston(return_X_y=False)Các dòng script sau sẽ xác định ma trận đặc trưng, X và vectơ phản hồi, Y -
X = boston.data
y = boston.targetTiếp theo, chia tập dữ liệu thành các tập huấn luyện và thử nghiệm như sau:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)Thí dụ
Bây giờ, tạo đối tượng hồi quy tuyến tính và đào tạo mô hình như sau:
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()Đầu ra
Coefficients:
[
-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01
]
Variance score: 0.709454060230326
Giả định
Sau đây là một số giả định về tập dữ liệu được thực hiện bởi mô hình hồi quy tuyến tính:
Multi-collinearity- Mô hình hồi quy tuyến tính giả định rằng có rất ít hoặc không có tính đa cộng tuyến trong dữ liệu. Về cơ bản, đa cộng tuyến xảy ra khi các biến hoặc đặc trưng độc lập có sự phụ thuộc vào chúng.
Auto-correlation- Một giả định khác Mô hình hồi quy tuyến tính giả định rằng có rất ít hoặc không có tương quan tự động trong dữ liệu. Về cơ bản, tự động tương quan xảy ra khi có sự phụ thuộc giữa các sai số dư.
Relationship between variables - Mô hình hồi quy tuyến tính giả định rằng mối quan hệ giữa các biến phản hồi và đặc trưng phải là tuyến tính.