Bruchteil eines Kreises
Ein vollständiger oder ganzer Kreis wird als 1 angenommen und Teile der Kreise werden als Brüche dargestellt. Wenn beispielsweise ein Kreis in 8 gleiche Teile unterteilt ist, repräsentiert jeder der Teile den Bruchteil 1/8. Drei Teile eines solchen Kreises würden 3/8 und mehr darstellen.
Hier haben wir es mit einer Art von Problemen zu tun, bei denen Brüche angegeben werden, die bestimmte Teile eines Kreises darstellen, und wir den Bruch finden müssen, der den verbleibenden unbekannten Teil des Kreises darstellt. Um solche Probleme zu lösen, addieren wir die Brüche, die die Bruchteile darstellen, und subtrahieren dann die Summe von 1, dem gesamten Kreis. Das Ergebnis gibt den Bruch an, der den unbekannten Bruchteil des Kreises darstellt.
Wie viel des Kreises ist nicht schattiert? Schreiben Sie Ihre Antwort als Bruch in einfachster Form.
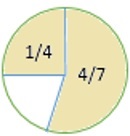
Lösung
Step 1:
Zuerst finden wir heraus, welcher Gesamtteil der Figur schattiert ist.
$ \ frac {1} {4} $ + $ \ frac {4} {7} $ = $ \ frac {7} {28} $ + $ \ frac {16} {28} $ = $ \ frac {(7 +16)} {28} $ = $ \ frac {23} {28} $
Step 2:
Um den nicht schattierten Bruchteil der Zahl zu ermitteln, subtrahieren wir das erhaltene Ergebnis ( $ \ frac {23} {28} $ ) von 1.
1 - $ \ frac {23} {28} $ = $ \ frac {28} {28} $ - $ \ frac {23} {28} $ = $ \ frac {(28-23} {28} $ = $ \ frac {5} {28} $
Der nicht schattierte Teil der Figur ist also $ \ frac {5} {28} $ .
Wie viel des Kreises ist schattiert? Schreiben Sie Ihre Antwort als Bruch in einfachster Form.
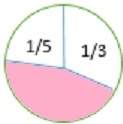
Lösung
Step 1:
Zuerst finden wir heraus, wie viel von der Figur nicht schattiert ist.
$ \ frac {1} {5} $ + $ \ frac {1} {3} $ = $ \ frac {3} {15} $ + $ \ frac {5} {15} $ = $ \ frac {(3 +5)} {15} $ = $ \ frac {8} {15} $
Step 2:
Um den nicht schattierten Bruchteil der Zahl zu ermitteln, subtrahieren wir das erhaltene Ergebnis ( $ \ frac {8} {15} $ ) von 1.
1 - $ \ frac {8} {15} $ = $ \ frac {15} {15} $ - $ \ frac {8} {15} $ = $ \ frac {(15−8)} {15} $ = $ \ frac {7} {15} $
Der schattierte Bruchteil der Figur ist also $ \ frac {7} {15} $ .