Digitale Kommunikation - Sampling
Sampling ist definiert als: "Der Prozess des Messens der Momentanwerte des zeitkontinuierlichen Signals in einer diskreten Form."
Sample ist ein Datenelement aus den gesamten Daten, das im Zeitbereich kontinuierlich ist.
Wenn eine Quelle ein analoges Signal erzeugt und wenn dieses digitalisiert werden muss, mit 1s und 0sdh hoch oder niedrig, das Signal muss rechtzeitig diskretisiert werden. Diese Diskretisierung des analogen Signals wird als Sampling bezeichnet.
Die folgende Abbildung zeigt ein zeitkontinuierliches Signal x (t) und ein abgetastetes Signal xs (t). Wannx (t) wird mit einer periodischen Impulsfolge multipliziert, dem abgetasteten Signal xs (t) erhalten wird.
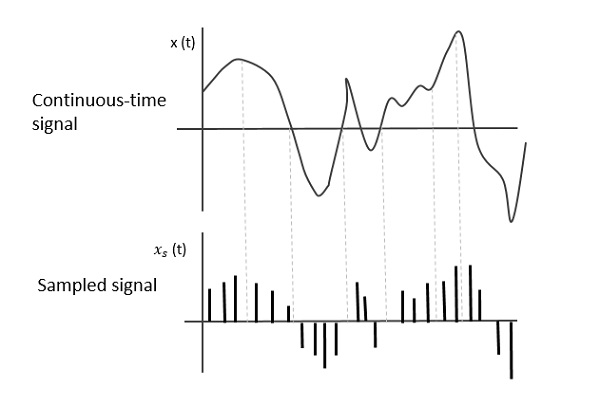
Abtastrate
Um die Signale zu diskretisieren, sollte der Abstand zwischen den Abtastwerten festgelegt werden. Diese Lücke kann als bezeichnet werdensampling period Ts.
$$ Sampling \: Frequenz = \ frac {1} {T_ {s}} = f_s $$Wo,
$ T_ {s} $ ist die Abtastzeit
$ f_ {s} $ ist die Abtastfrequenz oder die Abtastrate
Sampling frequencyist der Kehrwert der Abtastperiode. Diese Abtastfrequenz kann einfach als bezeichnet werdenSampling rate. Die Abtastrate gibt die Anzahl der Abtastungen pro Sekunde oder für einen endlichen Satz von Werten an.
Damit ein analoges Signal aus dem digitalisierten Signal rekonstruiert werden kann, sollte die Abtastrate stark berücksichtigt werden. Die Abtastrate sollte so sein, dass die Daten im Nachrichtensignal weder verloren gehen noch überlappen. Daher wurde hierfür eine Rate festgelegt, die als Nyquist-Rate bezeichnet wird.
Nyquist Rate
Angenommen, ein Signal ist bandbegrenzt, ohne dass Frequenzkomponenten höher als sind WHertz. Das bedeutet,Wist die höchste Frequenz. Für ein solches Signal sollte für eine effektive Wiedergabe des ursprünglichen Signals die Abtastrate doppelt so hoch sein wie die höchste Frequenz.
Was bedeutet,
$$ f_ {S} = 2W $$Wo,
$ f_ {S} $ ist die Abtastrate
W ist die höchste Frequenz
Diese Abtastrate wird als bezeichnet Nyquist rate.
Über die Theorie dieser Nyquist-Rate wurde ein Satz namens Sampling Theorem aufgestellt.
Abtasttheorem
Der Abtastsatz, der auch als bezeichnet wird Nyquist theoremliefert die Theorie einer ausreichenden Abtastrate in Bezug auf die Bandbreite für die Klasse von Funktionen, die bandbegrenzt sind.
Der Abtastsatz besagt: „Ein Signal kann exakt reproduziert werden, wenn es mit der Rate abgetastet wird fs Das ist mehr als das Doppelte der maximalen Frequenz W. ”
Um diesen Abtastsatz zu verstehen, betrachten wir ein bandbegrenztes Signal, dh ein Signal, dessen Wert ist non-zero zwischen einigen –W und W Hertz.
Ein solches Signal wird dargestellt als $x(f) = 0 for |f\lvert > W$
Für das zeitkontinuierliche Signal x (t)Das bandbegrenzte Signal im Frequenzbereich kann wie in der folgenden Abbildung dargestellt dargestellt werden.
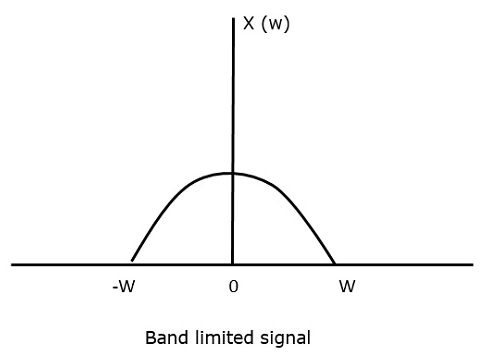
Wir brauchen eine Abtastfrequenz, eine Frequenz, bei der auch nach der Abtastung kein Informationsverlust auftreten sollte. Dafür haben wir die Nyquist-Rate, dass die Abtastfrequenz das Zweifache der Maximalfrequenz betragen sollte. Dies ist die kritische Abtastrate.
Wenn das Signal x(t) Wird oberhalb der Nyquist-Rate abgetastet, kann das ursprüngliche Signal wiederhergestellt werden, und wenn es unterhalb der Nyquist-Rate abgetastet wird, kann das Signal nicht wiederhergestellt werden.
Die folgende Abbildung erläutert ein Signal, wenn es mit einer höheren Rate als abgetastet wird 2w im Frequenzbereich.
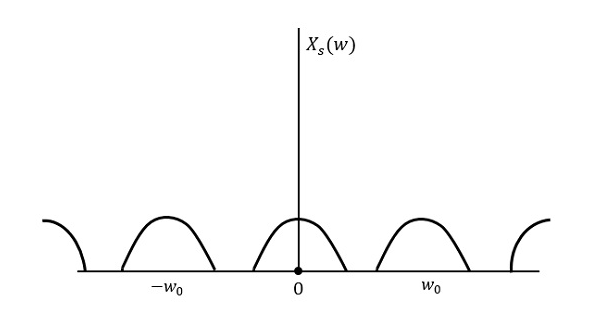
Die obige Abbildung zeigt die Fourier-Transformation eines Signals $x_{s}(t)$. Hier werden die Informationen ohne Verlust reproduziert. Es gibt keine Verwechslung und daher ist eine Wiederherstellung möglich.
Die Fourier-Transformation des Signals $x_{s}(t)$ ist
$$ X_ {s} (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0) $$Wobei $ T_ {s} $ = Sampling Period und $ w_ {0} = \ frac {2 \ pi} {T_s} $
Lassen Sie uns sehen, was passiert, wenn die Abtastrate doppelt so hoch ist wie die höchste Frequenz (2W)
Das bedeutet,
$$ f_ {s} = 2W $$Wo,
$ f_ {s} $ ist die Abtastfrequenz
W ist die höchste Frequenz
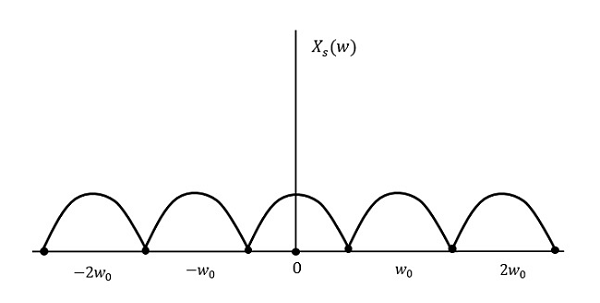
Das Ergebnis ist wie in der obigen Abbildung gezeigt. Die Informationen werden ohne Verlust ersetzt. Daher ist dies auch eine gute Abtastrate.
Betrachten wir nun den Zustand.
$$ f_ {s} <2W $$Das resultierende Muster sieht wie in der folgenden Abbildung aus.

Anhand des obigen Musters können wir beobachten, dass das Überlappen von Informationen erfolgt, was zu Verwechslungen und Informationsverlust führt. Dieses unerwünschte Phänomen des Überlappens wird als Aliasing bezeichnet.
Aliasing
Aliasing kann als "das Phänomen einer Hochfrequenzkomponente im Spektrum eines Signals bezeichnet werden, das die Identität einer Niederfrequenzkomponente im Spektrum seiner abgetasteten Version annimmt".
Die Korrekturmaßnahmen zur Verringerung der Auswirkung von Aliasing sind:
Im Senderbereich von PCM a low pass anti-aliasing filter wird vor dem Abtastgerät eingesetzt, um die unerwünschten Hochfrequenzkomponenten zu beseitigen.
Das Signal, das nach dem Filtern abgetastet wird, wird mit einer Rate abgetastet, die geringfügig höher als die Nyquist-Rate ist.
Diese Wahl, die Abtastrate höher als die Nyquist-Rate zu haben, hilft auch bei der einfacheren Gestaltung des reconstruction filter am Empfänger.
Umfang der Fourier-Transformation
Es wird allgemein beobachtet, dass wir die Hilfe von Fourier-Reihen und Fourier-Transformationen bei der Analyse der Signale und auch beim Beweis von Theoremen suchen. Es ist, weil -
Die Fourier-Transformation ist die Erweiterung der Fourier-Reihe für nichtperiodische Signale.
Die Fourier-Transformation ist ein leistungsstarkes mathematisches Werkzeug, mit dem die Signale in verschiedenen Bereichen angezeigt und die Signale einfach analysiert werden können.
Mit dieser Fourier-Transformation kann jedes Signal in Form der Summe von Sinus und Cosinus zerlegt werden.
Lassen Sie uns im nächsten Kapitel das Konzept der Quantisierung diskutieren.