DC-Amperemeter
Strom ist die Flussrate der elektrischen Ladung. Wenn diese elektrische Ladung nur in eine Richtung fließt, wird der resultierende Strom als Gleichstrom (DC) bezeichnet. Das Instrument, mit dem der aufgerufene Gleichstrom gemessen wirdDC ammeter.
Wenn wir einen Widerstand parallel zum PMMC-Galvanometer (Permanent Magnet Moving Coil) platzieren, fungiert die gesamte Kombination als Gleichstrom-Amperemeter. Der Parallelwiderstand, der im Gleichstrom-Amperemeter verwendet wird, wird auch als Shunt-Widerstand oder einfach als Shunt-Widerstand bezeichnet.shunt. Der Wert dieses Widerstands sollte als klein angesehen werden, um den Gleichstrom mit großem Wert zu messen.
Das circuit diagram des Gleichstrom-Amperemeter ist in der folgenden Abbildung dargestellt.
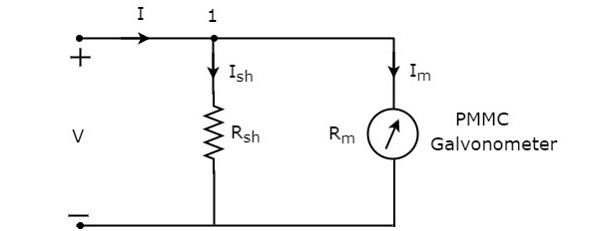
Wir müssen das platzieren DC ammeterin Reihe mit dem Zweig eines Stromkreises, in dem der Gleichstrom gemessen werden soll. Die Spannung an den parallel geschalteten Elementen ist gleich. Die Spannung am Shunt-Widerstand $ R_ {sh} $ und die Spannung am Galvanometer-Widerstand $ R_ {m} $ sind also gleich, da diese beiden Elemente in der obigen Schaltung parallel geschaltet sind.Mathematicallykann geschrieben werden als
$$ I_ {sh} R_ {sh} = I_ {m} R_ {m} $$
$ \ Rightarrow R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {sh}} $ (Gleichung 1)
Das KCL equation am Knoten 1 ist
$$ - I + I_ {sh} + I_ {m} = 0 $$
$$ \ Rightarrow I_ {sh} = I-I_ {m} $$
Substitute der Wert von $ I_ {sh} $ in Gleichung 1.
$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I-I_ {m}} $ (Gleichung 2)
Nehmen Sie $ I_ {m} $ als gemeinsam im Nennerterm, der auf der rechten Seite von Gleichung 2 vorhanden ist
$$ R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {m} (\ frac {1} {I_ {m}} - 1)} $$
$ \ Rightarrow R_ {sh} = \ frac {R_ {m}} {\ frac {I} {I_ {m}} - 1} $ (Gleichung 3)
Wo,
$ R_ {sh} $ ist der Shunt-Widerstand
$ R_ {m} $ ist der Innenwiderstand des Galvanometers
$ I $ ist der gesamte Gleichstrom, der gemessen werden soll
$ I_ {m} $ ist der vollständige Ablenkstrom
Das Verhältnis des gesamten zu messenden Gleichstroms $ I $ und des vollen Ablenkstroms des Galvanometers $ I_ {m} $ ist bekannt als multiplying factor, m. Mathematisch kann es dargestellt werden als
$ m = \ frac {I} {I_ {m}} $ (Gleichung 4)
$ R_ {sh} = \ frac {R_ {m}} {m-1} $ (Gleichung 5)
Wir können das finden value of shunt resistance durch Verwenden von Gleichung 2 oder Gleichung 5 basierend auf den verfügbaren Daten.
Multi Range DC Amperemeter
Im vorherigen Abschnitt haben wir uns mit Gleichstrom-Amperemeter befasst, das durch Parallelschalten eines Widerstands parallel zum PMMC-Galvanometer erhalten wird. Mit diesem Gleichstrom-Amperemeter kann a gemessen werdenparticular range von Gleichströmen.
Wenn wir das DC-Amperemeter zur Messung der Gleichströme von verwenden möchten multiple rangesDann müssen wir mehrere parallele Widerstände anstelle eines einzelnen Widerstands verwenden, und diese gesamte Kombination von Widerständen verläuft parallel zum PMMC-Galvanometer. Dascircuit diagram des Gleichstrom-Amperemeter mit mehreren Bereichen ist in der folgenden Abbildung dargestellt.
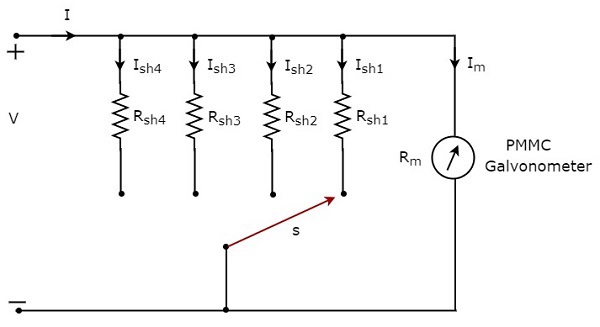
Stellen Sie dieses Gleichstrom-Amperemeter mit mehreren Bereichen in Reihe mit dem Zweig eines Stromkreises, in dem der Gleichstrom des erforderlichen Bereichs gemessen werden soll. Der gewünschte Strombereich wird durch Anschließen des Schalters s an den jeweiligen Nebenschlusswiderstand gewählt.
$ M_ {1}, m_ {2}, m_ {3} $ und $ m_ {4} $ sind die multiplying factorsdes Gleichstrom-Amperemeter, wenn wir die gesamten zu messenden Gleichströme als $ I_ {1}, I_ {2}, I_ {3} $ bzw. $ I_ {4} $ betrachten. Es folgen die Formeln, die jedem Multiplikationsfaktor entsprechen.
$$ m_ {1} = \ frac {I_ {1}} {I_ {m}} $$
$$ m_ {2} = \ frac {I_ {2}} {I_ {m}} $$
$$ m_ {3} = \ frac {I_ {3}} {I_ {m}} $$
$$ m_ {4} = \ frac {I_ {4}} {I_ {m}} $$
In der obigen Schaltung gibt es vier shunt resistors, $ R_ {sh1}, R_ {sh2}, R_ {sh2} $ und $ R_ {sh4} $. Es folgen die Formeln, die diesen vier Widerständen entsprechen.
$$ R_ {sh1} = \ frac {R_ {m}} {m_ {1} -1} $$
$$ R_ {sh2} = \ frac {R_ {m}} {m_ {2} -1} $$
$$ R_ {sh3} = \ frac {R_ {m}} {m_ {3} -1} $$
$$ R_ {sh4} = \ frac {R_ {m}} {m_ {4} -1} $$
Die obigen Formeln helfen uns, die Widerstandswerte jedes Shunt-Widerstands zu finden.