Lissajous Figuren
Lissajous figureist das Muster, das auf dem Bildschirm angezeigt wird, wenn sinusförmige Signale sowohl an horizontale als auch an vertikale Ablenkplatten von CRO angelegt werden. Diese Muster variieren basierend auf den Amplituden, Frequenzen und Phasendifferenzen der sinusförmigen Signale, die sowohl auf horizontale als auch vertikale Ablenkplatten von CRO angewendet werden.
Die folgende Abbildung zeigt eine example von Lissajous Figur.
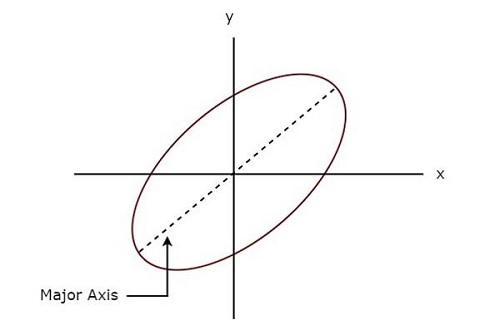
Die obige Lissajous Figur ist in elliptical shape und seine Hauptachse hat einen Neigungswinkel mit positiver x-Achse.
Messungen mit Lissajous-Figuren
Wir können Folgendes tun two measurements von einer Lissajous Figur.
- Frequenz des sinusförmigen Signals
- Phasendifferenz zwischen zwei sinusförmigen Signalen
Lassen Sie uns nun nacheinander über diese beiden Messungen sprechen.
Frequenzmessung
Die Lissajous-Figur wird auf dem Bildschirm angezeigt, wenn die sinusförmigen Signale sowohl an die horizontalen als auch an die vertikalen Ablenkplatten des CRO angelegt werden. Wenden Sie daher das sinusförmige Signal an, das Standard hatknown frequencyzu den horizontalen Ablenkplatten von CRO. In ähnlicher Weise legen Sie das sinusförmige Signal an, dessenfrequency ist unknown zu den vertikalen Ablenkplatten von CRO
$ F_ {H} $ und $ f_ {V} $ sind die Frequenzen von Sinussignalen, die an die horizontalen bzw. vertikalen Ablenkplatten von CRO angelegt werden. Die Beziehung zwischen $ f_ {H} $ und $ f_ {V} $ kann seinmathematically dargestellt wie unten.
$$ \ frac {f_ {V}} {f_ {H}} = \ frac {n_ {H}} {n_ {V}} $$
Aus der obigen Beziehung erhalten wir die Frequenz des sinusförmigen Signals, das an die vertikalen Ablenkplatten von CRO as angelegt wird
$ f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H} $ (Gleichung 1)
Wo,
$ n_ {H} $ ist die Anzahl der horizontalen Tangentialitäten
$ n_ {V} $ ist die Anzahl der vertikalen Tangentialitäten
Wir können die Werte von $ n_ {H} $ und $ n_ {V} $ aus der Lissajous-Zahl ermitteln. Wenn wir also die Werte von $ n_ {H} $, $ n_ {V} $ und $ f_ {H} $ in Gleichung 1 einsetzen, erhalten wir den Wert von$f_{V}$dh die frequency of sinusoidal signal das wird auf die vertikalen Ablenkplatten von CRO angewendet.
Messung der Phasendifferenz
Eine Lissajous-Figur wird auf dem Bildschirm angezeigt, wenn sinusförmige Signale sowohl an horizontale als auch an vertikale Ablenkplatten von CRO angelegt werden. Wenden Sie daher die sinusförmigen Signale an, die habensame amplitude and frequency sowohl zu horizontalen als auch zu vertikalen Ablenkplatten von CRO.
Für einige wenige Lissajous-Figuren können wir anhand ihrer Form direkt die Phasendifferenz zwischen den beiden sinusförmigen Signalen erkennen.
Wenn die Lissajous Figur a ist straight line mit einer Neigung von $ 45 ^ {\ circ} $ mit positiver x-Achse, dann die phase differencezwischen den beiden sinusförmigen Signalen liegt $ 0 ^ {\ circ} $. Das heißt, es gibt keine Phasendifferenz zwischen diesen beiden sinusförmigen Signalen.
Wenn die Lissajous Figur a ist straight line mit einer Neigung von $ 135 ^ {\ circ} $ mit positiver x-Achse, dann die phase differencezwischen den beiden sinusförmigen Signalen liegt $ 180 ^ {\ circ} $. Das heißt, diese beiden sinusförmigen Signale sind phasenverschoben.
Wenn die Lissajous Figur in ist circular shapedann beträgt die Phasendifferenz zwischen den beiden sinusförmigen Signalen $ 90 ^ {\ circ} $ oder $ 270 ^ {\ circ} $.
Wir können die Phasendifferenz zwischen den beiden sinusförmigen Signalen unter Verwendung von Formeln berechnen, wenn die Lissajous-Zahlen von sind elliptical shape.
Wenn die Hauptachse einer elliptischen Form einer Lissajous-Figur mit einem Neigungswinkel zwischen $ 0 ^ {\ circ} $ und $ 90 ^ {\ circ} $ mit positiver x-Achse liegt, beträgt die Phasendifferenz zwischen den beiden sinusförmigen Signalen.
$$ \ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ right) $$
Wenn die Hauptachse einer Lissajous-Figur mit elliptischer Form und einem Neigungswinkel zwischen $ 90 ^ {\ circ} $ und $ 180 ^ {\ circ} $ mit positiver x-Achse liegt, beträgt die Phasendifferenz zwischen den beiden sinusförmigen Signalen.
$$ \ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ right) $$
Where,
$ x_ {1} $ ist der Abstand vom Ursprung zum Punkt auf der x-Achse, an dem sich die Lissajous-Figur mit elliptischer Form schneidet
$ x_ {2} $ ist der Abstand vom Ursprung zur vertikalen Tangente der elliptischen Form der Lissajous-Figur
$ y_ {1} $ ist der Abstand vom Ursprung zum Punkt auf der y-Achse, an dem sich die Lissajous-Figur mit elliptischer Form schneidet
$ y_ {2} $ ist der Abstand vom Ursprung zur horizontalen Tangente der elliptischen Form der Lissajous-Figur
In diesem Kapitel erfahren Sie, wie Sie die Frequenz eines unbekannten sinusförmigen Signals und die Phasendifferenz zwischen zwei sinusförmigen Signalen von Lissajous-Figuren mithilfe von Formeln ermitteln.