DC-Voltmeter

Das Gleichspannungsmessgerät ist ein Messgerät, mit dem die Gleichspannung an zwei beliebigen Punkten des Stromkreises gemessen wird. Wenn wir einen Widerstand in Reihe mit dem PMMC-Galvanometer (Permanent Magnet Moving Coil) schalten, wirkt die gesamte Kombination zusammen alsDC voltmeter.

Der Serienwiderstand, der im Gleichspannungsvoltmeter verwendet wird, wird auch als Serienmultiplikatorwiderstand oder einfach als Multiplikator bezeichnet. Grundsätzlich wird die Strommenge begrenzt, die durch das Galvanometer fließt, um zu verhindern, dass der Zählerstrom den vollen Ablenkwert überschreitet. Dascircuit diagram des Gleichspannungsmessers ist in der folgenden Abbildung dargestellt.

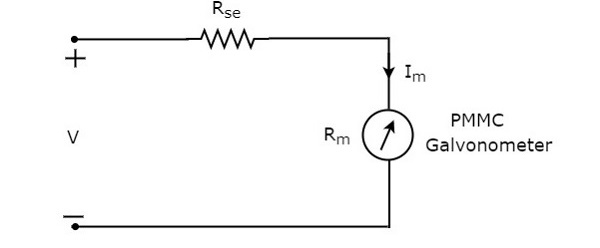
Wir müssen dieses Gleichspannungsmessgerät an den beiden Punkten eines Stromkreises platzieren, an denen die Gleichspannung gemessen werden soll.

Anwenden KVL um die Schleife der obigen Schaltung.

$ V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0 $ (Gleichung 1)

$$ \ Rightarrow V-I_ {m} R_ {m} = I_ {m} R_ {se} $$

$$ \ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}} $$

$ \ Rightarrow R_ {se} = \ frac {V} {I_ {m}} - R_ {m} $ (Gleichung 2)

Wo,

$ R_ {se} $ ist der Serienmultiplikatorwiderstand

$ V $ ist die Vollbereichsgleichspannung, die gemessen werden soll

$ I_ {m} $ ist der vollständige Ablenkstrom

$ R_ {m} $ ist der Innenwiderstand des Galvanometers

Das Verhältnis der zu messenden Gleichspannung im vollen Bereich $ V $ und des Gleichspannungsabfalls am Galvanometer $ V_ {m} $ ist bekannt als multiplying factorm. Mathematisch kann es dargestellt werden als

$ m = \ frac {V} {V_ {m}} $ (Gleichung 3)

Aus Gleichung 1 erhalten wir die folgende Gleichung für full range DC voltage das ist zu messen, $ V $.

$ V = I_ {m} R_ {se} + I_ {m} R_ {m} $ (Gleichung 4)

Das DC voltage dropüber das Galvanometer ist $ V_ {m} $ das Produkt aus dem vollen Ablenkstrom $ I_ {m} $ und dem Innenwiderstand des Galvanometers $ R_ {m} $. Mathematisch kann es geschrieben werden als

$ V_ {m} = I_ {m} R_ {m} $ (Gleichung 5)

Substitute, Gleichung 4 und Gleichung 5 in Gleichung 3.

$$ m = \ frac {I_ {m} R_ {se} + I_ {m} R_ {m}} {I_ {m} R_ {m}} $$

$ \ Rightarrow m = \ frac {R_ {se}} {R_ {m}} + 1 $

$ \ Rightarrow m-1 = \ frac {R_ {se}} {R_ {m}} $

$ R_ {se} = R_ {m} \ left (m-1 \ right) $ (Gleichung 6)

Wir können das finden value of series multiplier resistance unter Verwendung von entweder Gleichung 2 oder Gleichung 6 basierend auf den verfügbaren Daten.

Multi Range DC Voltmeter

Im vorherigen Abschnitt hatten wir das Gleichspannungsmessgerät erörtert, das durch Reihenschaltung eines Multiplikatorwiderstands mit dem PMMC-Galvanometer erhalten wird. Mit diesem Gleichspannungsmessgerät kann a gemessen werdenparticular range von Gleichspannungen.

Wenn wir das Gleichspannungsmessgerät zur Messung der Gleichspannungen von verwenden möchten multiple rangesDann müssen wir mehrere parallele Multiplikatorwiderstände anstelle eines einzelnen Multiplikatorwiderstands verwenden, und diese gesamte Widerstandskombination ist in Reihe mit dem PMMC-Galvanometer geschaltet. Dascircuit diagram des Gleichstrom-Voltmeters mit mehreren Bereichen ist in der folgenden Abbildung dargestellt.

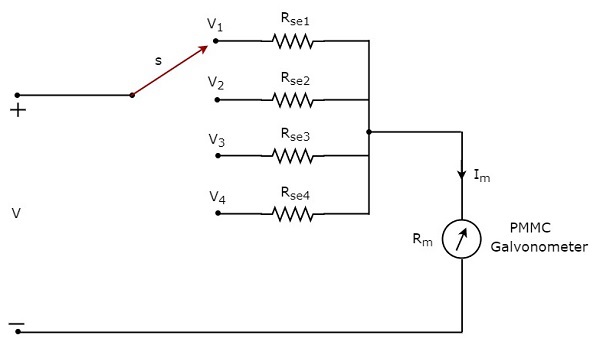
Wir müssen das platzieren multi range DC voltmeterüber die beiden Punkte eines Stromkreises, an denen die Gleichspannung des erforderlichen Bereichs gemessen werden soll. Wir können den gewünschten Spannungsbereich wählen, indem wir die Schalter s an den jeweiligen Multiplikatorwiderstand anschließen.

$ M_ {1}, m_ {2}, m_ {2} $ und $ m_ {4} $ sind die multiplying factorsdes Gleichspannungsmessers, wenn wir die zu messenden Gleichspannungen im gesamten Bereich als $ V_ {1}, V_ {2}, V_ {3} $ bzw. $ V_ {4} $ betrachten. Es folgen die Formeln, die jedem Multiplikationsfaktor entsprechen.

$$ m_ {1} = \ frac {V_ {1}} {V_ {m}} $$

$$ m_ {2} = \ frac {V_ {2}} {V_ {m}} $$

$$ m_ {3} = \ frac {V_ {3}} {V_ {m}} $$

$$ m_ {4} = \ frac {V_ {4}} {V_ {m}} $$

In der obigen Schaltung gibt es vier series multiplier resistors, $ R_ {se1}, R_ {se2}, R_ {se3} $ und $ R_ {se4} $. Es folgen die Formeln, die diesen vier Widerständen entsprechen.

$$ R_ {se1} = R_ {m} \ left (m_ {1} -1 \ right) $$

$$ R_ {se2} = R_ {m} \ left (m_ {2} -1 \ right) $$

$$ R_ {se3} = R_ {m} \ left (m_ {3} -1 \ right) $$

$$ R_ {se4} = R_ {m} \ left (m_ {4} -1 \ right) $$

Wir können also die Widerstandswerte jedes Serienmultiplikatorwiderstands unter Verwendung der obigen Formeln ermitteln.