Arithmetische Schaltungen

Im vorherigen Kapitel haben wir die grundlegenden Anwendungen von Operationsverstärkern besprochen. Beachten Sie, dass sie unter den linearen Betrieb eines Operationsverstärkers fallen. Lassen Sie uns in diesem Kapitel über arithmetische Schaltungen sprechen, die auch lineare Anwendungen von Operationsverstärkern sind.

Die elektronischen Schaltungen, die arithmetische Operationen ausführen, werden als bezeichnet arithmetic circuits. Mit Operationsverstärkern können Sie grundlegende Rechenschaltungen wie zadder und ein subtractor. In diesem Kapitel erfahren Sie mehr über jeden einzelnen von ihnen.

Addierer

Ein Addierer ist eine elektronische Schaltung, die einen Ausgang erzeugt, der gleich der Summe der angelegten Eingänge ist. In diesem Abschnitt wird die Addiererschaltung auf Operationsverstärkerbasis erläutert.

Ein Addierer auf Operationsverstärkerbasis erzeugt einen Ausgang, der der Summe der an seinem invertierenden Anschluss angelegten Eingangsspannungen entspricht. Es wird auch als bezeichnetsumming amplifier, da der Ausgang verstärkt ist.

Das circuit diagram eines auf einem Operationsverstärker basierenden Addierers ist in der folgenden Abbildung dargestellt:

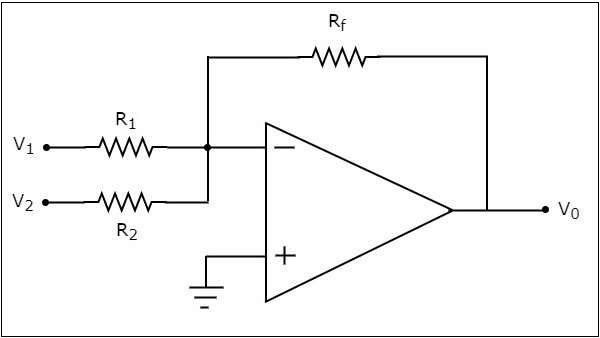
In der obigen Schaltung ist der nicht invertierende Eingangsanschluss des Operationsverstärkers mit Masse verbunden. Dies bedeutet, dass an seinem nicht invertierenden Eingangsanschluss Null Volt angelegt werden.

Laut dem virtual short conceptDie Spannung am invertierenden Eingangsanschluss eines Operationsverstärkers ist dieselbe wie die Spannung an seinem nicht invertierenden Eingangsanschluss. Die Spannung am invertierenden Eingangsanschluss des Operationsverstärkers beträgt also null Volt.

Das nodal equation am Knoten des invertierenden Eingangsterminals ist

$$ \ frac {0-V_1} {R_1} + \ frac {0-V_2} {R_2} + \ frac {0-V_0} {R_f} = 0 $$

$$ => \ frac {V_1} {R_1} - \ frac {V_2} {R_2} = \ frac {V_0} {R_f} $$

$$ => V_ {0} = R_ {f} \ left (\ frac {V_1} {R_1} + \ frac {V_2} {R_2} \ right) $$

Wenn $ R_ {f} = R_ {1} = R_ {2} = R $, dann ist die Ausgangsspannung $ V_ {0} $ -

$$ V_ {0} = - R {} \ left (\ frac {V_1} {R} + \ frac {V_2} {R} \ right) $$

$$ => V_ {0} = - (V_ {1} + V_ {2}) $$

Daher erzeugt die oben diskutierte Addiererschaltung auf Operationsverstärkerbasis die Summe der beiden Eingangsspannungen $ v_ {1} $ und $ v_ {1} $ als Ausgang, wenn alle in der Schaltung vorhandenen Widerstände den gleichen Wert haben . Es ist zu beachten, dass die Ausgangsspannung $ V_ {0} $ einer Addiererschaltung a hatnegative signDies zeigt an, dass zwischen dem Eingang und dem Ausgang eine Phasendifferenz von 180 ⁰ besteht .

Subtrahierer

Ein Subtrahierer ist eine elektronische Schaltung, die einen Ausgang erzeugt, der gleich der Differenz der angelegten Eingänge ist. In diesem Abschnitt wird die auf einem Operationsverstärker basierende Subtrahiererschaltung erläutert.

Ein auf einem Operationsverstärker basierender Subtrahierer erzeugt einen Ausgang, der der Differenz der Eingangsspannungen entspricht, die an seinen invertierenden und nicht invertierenden Anschlüssen angelegt werden. Es wird auch als bezeichnetdifference amplifier, da der Ausgang verstärkt ist.

Das circuit diagram eines auf einem Operationsverstärker basierenden Subtrahierers ist in der folgenden Abbildung dargestellt:

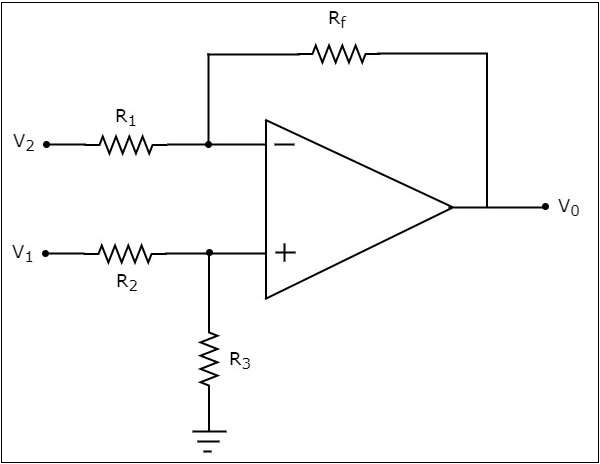
Lassen Sie uns nun den Ausdruck für die Ausgangsspannung $ V_ {0} $ der obigen Schaltung unter Verwendung von finden superposition theorem mit den folgenden Schritten -

Schritt 1

Berechnen wir zunächst die Ausgangsspannung $ V_ {01} $, indem wir nur $ V_ {1} $ berücksichtigen.

Beseitigen Sie dazu $ V_ {2} $, indem Sie es kurzschließen. Dann erhalten wir diemodified circuit diagram wie in der folgenden Abbildung gezeigt -

Verwenden Sie jetzt die voltage division principleBerechnen Sie die Spannung am nicht invertierenden Eingangsanschluss des Operationsverstärkers.

$$ => V_ {p} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) $$

Die obige Schaltung sieht nun aus wie ein nicht invertierender Verstärker mit der Eingangsspannung $ V_ {p} $. Daher ist die Ausgangsspannung $ V_ {01} $ der obigen Schaltung

$$ V_ {01} = V_ {p} \ left (1+ \ frac {R_f} {R_1} \ right) $$

Ersetzen Sie den Wert von $ V_ {p} $ in der obigen Gleichung, erhalten Sie die Ausgangsspannung $ V_ {01} $, indem Sie nur $ V_ {1} $ als - betrachten

$$ V_ {01} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) $$

Schritt 2

In diesem Schritt ermitteln wir die Ausgangsspannung $ V_ {02} $, indem wir nur $ V_ {2} $ berücksichtigen. Beseitigen Sie ähnlich wie im obigen Schritt $ V_ {1} $, indem Sie es kurzschließen. Dasmodified circuit diagram ist in der folgenden Abbildung dargestellt.

Sie können beobachten, dass die Spannung am nicht invertierenden Eingangsanschluss des Operationsverstärkers Null Volt beträgt. Es bedeutet, dass die obige Schaltung einfach eine istinverting op-amp. Daher beträgt die Ausgangsspannung $ V_ {02} $ der obigen Schaltung -

$$ V_ {02} = \ left (- \ frac {R_f} {R_1} \ right) V_ {2} $$

Schritt 3

In diesem Schritt erhalten wir die Ausgangsspannung $ V_ {0} $ der Subtrahiererschaltung durch adding the output voltageserhalten in Schritt 1 und Schritt 2. Mathematisch kann es geschrieben werden als

$$ V_ {0} = V_ {01} + V_ {02} $$

Wenn wir die Werte von $ V_ {01} $ und $ V_ {02} $ in die obige Gleichung einsetzen, erhalten wir -

$$ V_ {0} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) + \ left (- \ frac {R_f} {R_1} \ right) V_ {2} $$

$$ => V_ {0} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) - \ left (\ frac {R_f} {R_1} \ right) V_ {2} $$

Wenn $ R_ {f} = R_ {1} = R_ {2} = R_ {3} = R $, ist die Ausgangsspannung $ V_ {0} $

$$ V_ {0} = V_ {1} \ left (\ frac {R} {R + R} \ right) \ left (1+ \ frac {R} {R} \ right) - \ left (\ frac { R} {R} \ right) V_ {2} $$

$$ => V_ {0} = V_ {1} \ left (\ frac {R} {2R} \ right) (2) - (1) V_ {2} $$

$$ V_ {0} = V_ {1} -V_ {2} $$

Somit erzeugt die oben diskutierte Subtrahiererschaltung auf Operationsverstärkerbasis einen Ausgang, der die Differenz zweier Eingangsspannungen $ V_ {1} $ und $ V_ {2} $ ist, wenn alle in der Schaltung vorhandenen Widerstände den gleichen Wert haben .