Regressionstechniken

Regression ist eine statistische Technik, mit deren Hilfe die Beziehung zwischen den miteinander verbundenen wirtschaftlichen Variablen qualifiziert werden kann. Der erste Schritt besteht darin, den Koeffizienten der unabhängigen Variablen zu schätzen und dann die Zuverlässigkeit des geschätzten Koeffizienten zu messen. Dies erfordert die Formulierung einer Hypothese, und basierend auf der Hypothese können wir eine Funktion erstellen.

Wenn ein Manager die Beziehung zwischen den Werbeausgaben des Unternehmens und seinen Umsatzerlösen bestimmen möchte, wird er dem Hypothesentest unterzogen. Unter der Annahme, dass höhere Werbeausgaben zu einem höheren Verkauf für ein Unternehmen führen. Der Manager sammelt in einem bestimmten Zeitraum Daten zu Werbeausgaben und Umsatzerlösen. Diese Hypothese kann in die mathematische Funktion übersetzt werden, wo sie zu - führt

Y = A + Bx

Wo Y ist Verkauf, x ist der Werbeaufwand, A und B sind konstant.

Nach der Übersetzung der Hypothese in die Funktion besteht die Grundlage dafür darin, die Beziehung zwischen den abhängigen und unabhängigen Variablen zu finden. Der Wert der abhängigen Variablen ist für Forscher von größter Bedeutung und hängt vom Wert anderer Variablen ab. Die unabhängige Variable wird verwendet, um die Variation in der abhängigen Variablen zu erklären. Es kann in zwei Typen eingeteilt werden -

• Simple regression - Eine unabhängige Variable

• Multiple regression - Mehrere unabhängige Variablen

Einfache Regression

Im Folgenden finden Sie die Schritte zum Aufbau einer Regressionsanalyse:

• Geben Sie das Regressionsmodell an
• Daten zu Variablen abrufen
• Schätzen Sie die quantitativen Beziehungen
• Testen Sie die statistische Signifikanz der Ergebnisse
• Verwendung der Ergebnisse bei der Entscheidungsfindung

Formel für einfache Regression ist -

Y = a + bX + u

Y= abhängige Variable

X= unabhängige Variable

a= abfangen

b= Steigung

u= Zufallsfaktor

Querschnittsdaten liefern Informationen zu einer Gruppe von Entitäten zu einem bestimmten Zeitpunkt, während Zeitreihendaten Informationen zu einer Entität im Zeitverlauf liefern. Wenn wir die Regressionsgleichung schätzen, müssen wir die beste lineare Beziehung zwischen den abhängigen und den unabhängigen Variablen herausfinden.

Methode der gewöhnlichen kleinsten Quadrate (OLS)

Die gewöhnliche Methode der kleinsten Quadrate ist so ausgelegt, dass eine Linie durch eine Punktstreuung so angepasst wird, dass die Summe der quadratischen Abweichungen der Punkte von der Linie minimiert wird. Es ist eine statistische Methode. Normalerweise führen Softwarepakete eine OLS-Schätzung durch.

Y = a + bX

Bestimmungskoeffizient (R ² )

Der Bestimmungskoeffizient ist ein Maß, das angibt, dass der Prozentsatz der Variation der abhängigen Variablen auf die Variationen der unabhängigen Variablen zurückzuführen ist. R ² ist ein Maß für die Güte des Anpassungsmodells. Es folgen die Methoden -

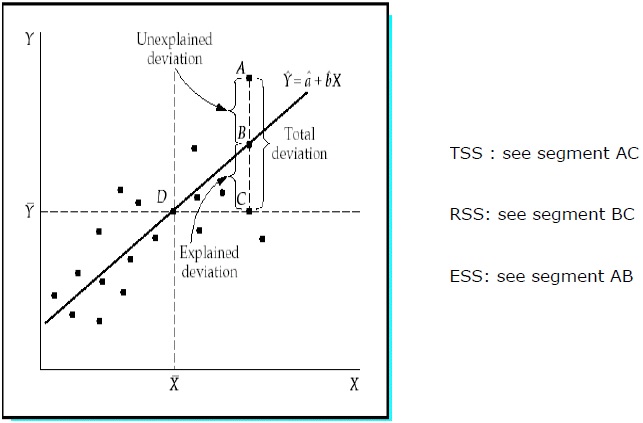
Gesamtsumme der Quadrate (TSS)

Summe der quadratischen Abweichungen der Stichprobenwerte von Y vom Mittelwert von Y.

TSS = SUM ( Y_i − Y)²

Y_i = abhängige Variablen

Y = Mittelwert der abhängigen Variablen

i = Anzahl der Beobachtungen

Regressionssumme der Quadrate (RSS)

Summe der quadratischen Abweichungen der geschätzten Werte von Y vom Mittelwert von Y.

RSS = SUM ( Ỷ_i − uY)²

Ỷ_i = geschätzter Wert von Y.

Y = Mittelwert der abhängigen Variablen

i = Anzahl der Variationen

Fehlersumme der Quadrate (ESS)

Summe der quadratischen Abweichungen der Stichprobenwerte von Y von den geschätzten Werten von Y.

ESS = SUM ( Y_i − Ỷ_i)²

Ỷ_i = geschätzter Wert von Y.

Y_i = abhängige Variablen

i = Anzahl der Beobachtungen

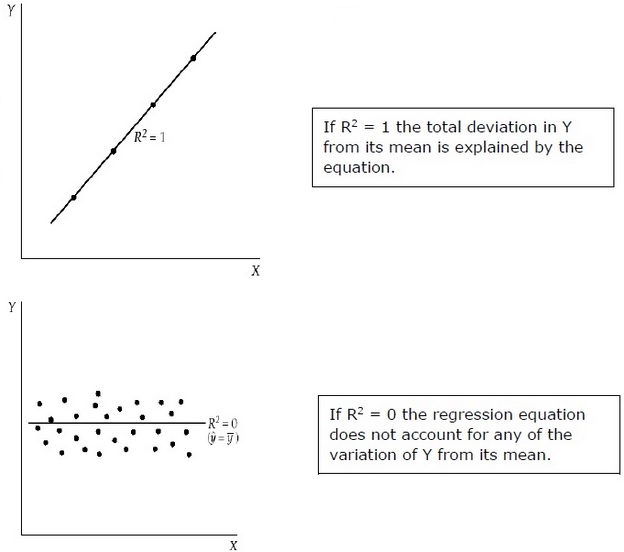
R ² misst den Anteil der Gesamtabweichung von Y von seinem Mittelwert, der durch das Regressionsmodell erklärt wird. Je näher das R ² an der Einheit liegt, desto größer ist die Erklärungskraft der Regressionsgleichung. Ein R ² nahe 0 zeigt an, dass die Regressionsgleichung nur eine sehr geringe Aussagekraft hat.

Zur Bewertung der Regressionskoeffizienten wird eine Stichprobe aus der Population anstelle der gesamten Population verwendet. Es ist wichtig, anhand der Stichprobe Annahmen über die Grundgesamtheit zu treffen und zu beurteilen, wie gut diese Annahmen sind.

Auswertung der Regressionskoeffizienten

Jede Stichprobe aus der Population erzeugt einen eigenen Abschnitt. Zur Berechnung der statistischen Differenz können folgende Methoden verwendet werden:

Two tailed test −

Nullhypothese: H ₀ : b = 0

Alternative Hypothese: H _a : b ≠ 0

One tailed test −

Nullhypothese: H ₀ : b> 0 (oder b <0)

Alternative Hypothese: H _a : b <0 (oder b> 0)

Statistic Test −

b = geschätzter Koeffizient

E (b) = b = 0 (Nullhypothese)

SE _b = Standardfehler des Koeffizienten

.

Wert von thängt vom Freiheitsgrad, einem oder zwei fehlgeschlagenen Tests und dem Signifikanzniveau ab. Um den kritischen Wert von zu bestimment, T-Tabelle kann verwendet werden. Dann kommt der Vergleich des t-Wertes mit dem kritischen Wert. Die Nullhypothese muss verworfen werden, wenn der Absolutwert des statistischen Tests größer oder gleich dem kritischen t-Wert ist. Lehnen Sie die Nullhypothese nicht ab. I Der absolute Wert des statistischen Tests ist kleiner als der kritische t-Wert.

Multiple Regressionsanalyse

Im Gegensatz zur einfachen Regression bei der multiplen Regressionsanalyse geben die Koeffizienten die Änderung der abhängigen Variablen an, sofern die Werte der anderen Variablen konstant sind.

Der Test der statistischen Signifikanz wird aufgerufen F-test. Der F-Test ist nützlich, da er die statistische Signifikanz der gesamten Regressionsgleichung misst und nicht nur für eine Person. Hier In der Nullhypothese gibt es keine Beziehung zwischen der abhängigen Variablen und den unabhängigen Variablen der Population.

Die Formel lautet - H ₀ : b1 = b2 = b3 =…. = bk = 0

Es besteht keine Beziehung zwischen der abhängigen Variablen und der k unabhängige Variablen für die Bevölkerung.

F-test static −

$$ F \: = \: \ frac {\ left (\ frac {R ^ 2} {K} \ right)} {\ frac {(1-R ^ 2)} {(nk-1)}} $$

Kritischer Wert von Fhängt vom Freiheitsgrad und dem Signifikanzniveau des Zählers und Nenners ab. Mit der F-Tabelle kann der kritische F-Wert ermittelt werden. Im Vergleich zum F-Wert mit dem kritischen Wert (F *) -

Wenn F> F *, müssen wir die Nullhypothese ablehnen.

Wenn F <F * ist, lehnen Sie die Nullhypothese nicht ab, da zwischen der abhängigen Variablen und allen unabhängigen Variablen keine signifikante Beziehung besteht.