Eigenschaften von Z-Transformationen
Z-Transform hat folgende Eigenschaften:
Linearitätseigenschaft
Wenn $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
und $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
Dann gibt die Linearitätseigenschaft an, dass
$ a \, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a \, X (Z) + b \, Y (Z) $
Zeitverschiebende Eigenschaft
Wenn $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
Dann besagt die zeitversetzte Eigenschaft, dass
$ x (nm) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z) $
Multiplikation mit Exponential Sequence Property
Wenn $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
Dann besagt die Multiplikation mit einer Exponentialsequenz-Eigenschaft, dass
$ a ^ n \ ,. x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $
Zeitumkehrungseigenschaft
Wenn $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
Dann besagt die Zeitumkehr-Eigenschaft, dass
$ x (-n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z) $
Differenzierung in der Z-Domäne ODER Multiplikation mit der Eigenschaft n
Wenn $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
Dann besagt die Multiplikation mit n oder die Differenzierung in der Eigenschaft der z-Domäne, dass
$ n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ über dZ ^ K} $
Faltungseigenschaft
Wenn $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
und $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
Dann besagt die Faltungseigenschaft, dass
$ x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z) $
Korrelationseigenschaft
Wenn $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $
und $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
Dann besagt die Korrelationseigenschaft, dass
$ x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1}) $
Anfangs- und Endwertsätze
Anfangs- und Endwertsätze der z-Transformation werden für das kausale Signal definiert.
Anfangswert-Theorem
Für ein kausales Signal x (n) besagt der Anfangswertsatz, dass
$ x (0) = \ lim_ {z \ to \ infty} X (z) $
Dies wird verwendet, um den Anfangswert des Signals zu finden, ohne eine inverse Z-Transformation durchzuführen
Endwertsatz
Für ein kausales Signal x (n) besagt der Endwertsatz, dass
$ x (\ infty) = \ lim_ {z \ to 1} [z-1] X (z) $
Dies wird verwendet, um den Endwert des Signals zu finden, ohne eine inverse Z-Transformation durchzuführen.
Konvergenzregion (ROC) der Z-Transformation
Der Variationsbereich von z, für den die Z-Transformation konvergiert, wird als Konvergenzbereich der Z-Transformation bezeichnet.
Eigenschaften des ROC von Z-Transformationen
Der ROC der z-Transformation ist mit einem Kreis in der z-Ebene angegeben.
ROC enthält keine Pole.
Wenn x (n) eine kausale Sequenz endlicher Dauer oder eine rechtsseitige Sequenz ist, ist der ROC die gesamte z-Ebene mit Ausnahme von z = 0.
Wenn x (n) eine endkausale antikausale Sequenz oder eine linksseitige Sequenz ist, dann ist der ROC die gesamte z-Ebene mit Ausnahme von z = ∞.
Wenn x (n) eine kausale Folge von unendlicher Dauer ist, befindet sich ROC außerhalb des Kreises mit dem Radius aie | z | > a.
Wenn x (n) eine antikausale Sequenz mit unendlicher Dauer ist, befindet sich ROC innerhalb des Kreises mit dem Radius aie | z | <a.
Wenn x (n) eine zweiseitige Folge endlicher Dauer ist, ist der ROC die gesamte z-Ebene mit Ausnahme von z = 0 & z = ∞.
Das Konzept der Republik China kann anhand des folgenden Beispiels erklärt werden:
Example 1: Finden Sie die z-Transformation und den ROC von $ a ^ nu [n] + a ^ {-} nu [-n-1] $
$ ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ über Za} + {Z \ über Z {-1 \ über a}} $
$$ ROC: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ über a} $$
Die Darstellung von ROC hat zwei Bedingungen als> 1 und a <1, da Sie a nicht kennen.

In diesem Fall gibt es keine Kombination ROC.
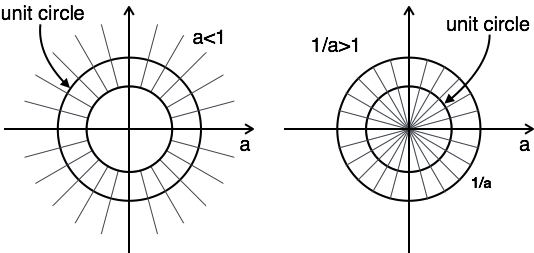
Hier ist die Kombination von ROC von $ a \ lt | z | \ lt {1 \ über a} $
Daher ist für dieses Problem eine z-Transformation möglich, wenn a <1 ist.
Kausalität und Stabilität
Die Kausalitätsbedingung für zeitdiskrete LTI-Systeme ist wie folgt:
Ein zeitdiskretes LTI-System ist kausal, wenn
ROC befindet sich außerhalb des äußersten Pols.
In der Übertragungsfunktion H [Z] kann die Reihenfolge des Zählers nicht größer sein als die Reihenfolge des Nenners.
Stabilitätsbedingung für zeitdiskrete LTI-Systeme
Ein zeitdiskretes LTI-System ist stabil, wenn
seine Systemfunktion H [Z] enthält den Einheitskreis | z | = 1.
Alle Pole der Übertragungsfunktion liegen innerhalb des Einheitskreises | z | = 1.
Z-Transformation von Basissignalen
| x (t) | X [Z] |
|---|---|
| $ \ delta $ | 1 |
| $ u (n) $ | $ {Z \ über Z-1} $ |
| $ u (-n-1) $ | $ - {Z \ über Z-1} $ |
| $ \ delta (nm) $ | $ z ^ {- m} $ |
| $ a ^ nu [n] $ | $ {Z \ über Za} $ |
| $ a ^ nu [-n-1] $ | $ - {Z \ over Za} $ |
| $ n \, a ^ nu [n] $ | $ {aZ \ over | Za | ^ 2} $ |
| $ n \, a ^ nu [-n-1] $ | $ - {aZ \ over | Za | ^ 2} $ |
| $ a ^ n \ cos \ omega nu [n] $ | $ {Z ^ 2-aZ \ cos \ omega \ über Z ^ 2-2aZ \ cos \ omega + a ^ 2} $ |
| $ a ^ n \ sin \ omega nu [n] $ | $ {aZ \ sin \ omega \ über Z ^ 2 -2aZ \ cos \ omega + a ^ 2} $ |