VLSI Design - MOS Wechselrichter

Der Wechselrichter ist wirklich der Kern aller digitalen Designs. Sobald seine Funktionsweise und Eigenschaften klar verstanden sind, wird das Entwerfen komplexerer Strukturen wie NAND-Gatter, Addierer, Multiplikatoren und Mikroprozessoren erheblich vereinfacht. Das elektrische Verhalten dieser komplexen Schaltkreise kann durch Extrapolation der für Wechselrichter erhaltenen Ergebnisse fast vollständig abgeleitet werden.

Die Analyse von Wechselrichtern kann erweitert werden, um das Verhalten komplexerer Gatter wie NAND, NOR oder XOR zu erklären, die wiederum die Bausteine ​​für Module wie Multiplikatoren und Prozessoren bilden. In diesem Kapitel konzentrieren wir uns auf eine einzelne Inkarnation des Inverter-Gates, nämlich den statischen CMOS-Inverter - oder kurz den CMOS-Inverter. Dies ist derzeit sicherlich die beliebteste und verdient daher unsere besondere Aufmerksamkeit.

Funktionsprinzip

Das Logiksymbol und die Wahrheitstabelle des idealen Wechselrichters sind in der folgenden Abbildung dargestellt. Hier ist A der Eingang und B der invertierte Ausgang, der durch ihre Knotenspannungen dargestellt wird. Bei Verwendung einer positiven Logik wird der Boolesche Wert von logisch 1 durch V _dd und logisch 0 durch 0 dargestellt. V _th ist die Wechselrichterschwellenspannung, die V _dd / 2 ist, wobei V _dd die Ausgangsspannung ist.

Der Ausgang wird von 0 auf V _dd geschaltet, wenn der Eingang kleiner als V _{th ist} . Für 0 <V _in <V ist _der Ausgang gleich dem logischen 0-Eingang und V _th <V _in <V _dd ist gleich dem logischen 1-Eingang für den Wechselrichter.

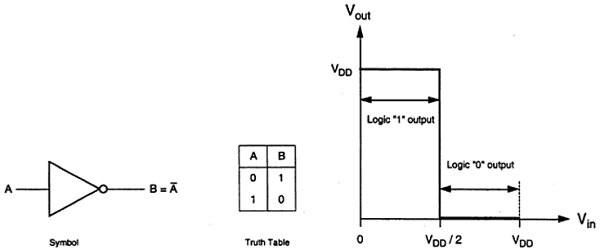
Die in der Abbildung gezeigten Eigenschaften sind ideal. Die verallgemeinerte Schaltungsstruktur eines nMOS-Wechselrichters ist in der folgenden Abbildung dargestellt.

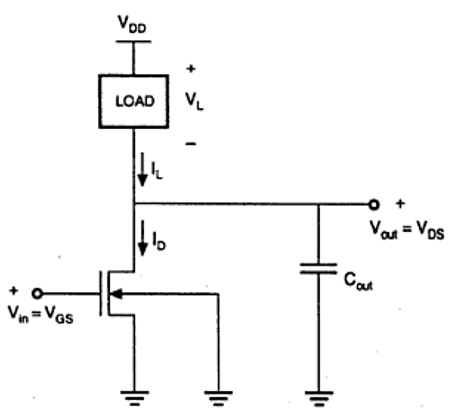
Aus der gegebenen Figur können wir sehen, dass die Eingangsspannung des Wechselrichters gleich der Gate-Source-Spannung des nMOS-Transistors und die Ausgangsspannung des Wechselrichters gleich der Drain-Source-Spannung des nMOS-Transistors ist. Die Source-Substrat-Spannung von nMOS wird auch als Treiber für einen geerdeten Transistor bezeichnet. also V _SS = 0. Der Ausgangsknoten ist mit einer konzentrierten Kapazität verbunden, die für VTC verwendet wird.

Widerstandslastwechselrichter

Die Grundstruktur eines ohmschen Lastwechselrichters ist in der folgenden Abbildung dargestellt. Hier wirkt der Verbesserungstyp nMOS als Treibertransistor. Die Last besteht aus einem einfachen linearen Widerstand R _L . Die Stromversorgung der Schaltung ist mit V _DD und der Drainstrom I _D ist gleich dem Laststrom I _R .

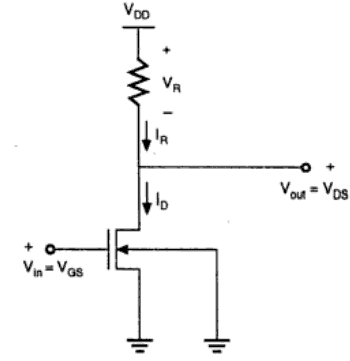
Schaltungsbetrieb

Wenn der Eingang des Treibertransistors kleiner als die Schwellenspannung V _TH (V _in <V _TH ) ist, befindet sich der Treibertransistor im Sperrbereich und leitet keinen Strom. Der Spannungsabfall über dem Lastwiderstand ist also NULL und die Ausgangsspannung ist gleich V _DD . Wenn nun die Eingangsspannung weiter ansteigt, beginnt der Treibertransistor, den Strom ungleich Null zu leiten, und nMOS geht in den Sättigungsbereich.

Mathematisch,

$$ I_ {D} = \ frac {K_ {n}} {2} \ left [V_ {GS} -V_ {TO} \ right] ^ {2} $$

Wenn die Eingangsspannung weiter erhöht wird, tritt der Treibertransistor in den linearen Bereich ein und der Ausgang des Treibertransistors nimmt ab.

$$ I_ {D} = \ frac {K_ {n}} {2} 2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} $$

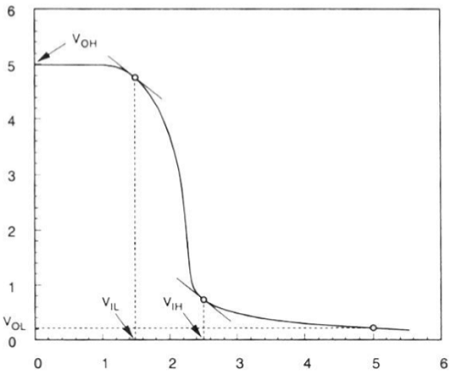
Die unten gezeigte VTC des ohmschen Lastwechselrichters zeigt den Betriebsmodus des Treibertransistors und die Spannungspunkte an.

Wechselrichter mit N-Typ-MOSFET-Last

Der Hauptvorteil der Verwendung eines MOSFET als Lastvorrichtung besteht darin, dass die vom Transistor eingenommene Siliziumfläche kleiner ist als die von der ohmschen Last eingenommene Fläche. Hier ist der MOSFET eine aktive Last und der Wechselrichter mit aktiver Last bietet eine bessere Leistung als der Wechselrichter mit ohmscher Last.

Erweiterungslast NMOS

In der Abbildung sind zwei Wechselrichter mit Lastvorrichtung vom Verstärkungstyp dargestellt. Der Lasttransistor kann abhängig von der an seinen Gate-Anschluss angelegten Vorspannung entweder im Sättigungsbereich oder im linearen Bereich betrieben werden. Der Wechselrichter mit gesättigter Verstärkung ist in der Abbildung dargestellt. (ein). Es erfordert eine einzige Spannungsversorgung und einen einfachen Herstellungsprozess, so dass V _OH auf V _DD - V _{T beschränkt ist} .

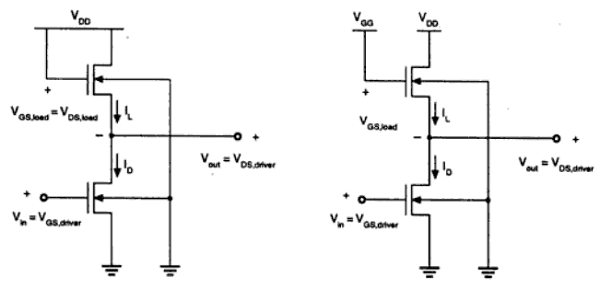
Der Wechselrichter mit linearer Verstärkung ist in der Abbildung dargestellt. (b). Es arbeitet immer im linearen Bereich; der _VOH- Pegel ist also gleich _VDD .

Der Wechselrichter mit linearer Last weist im Vergleich zum Wechselrichter mit gesättigter Verstärkung einen höheren Rauschabstand auf. Der Nachteil eines Wechselrichters mit linearer Verstärkung besteht jedoch darin, dass zwei separate Stromversorgungen erforderlich sind und beide Schaltkreise unter einer hohen Verlustleistung leiden. Daher werden Verbesserungswechselrichter in keinen digitalen Großanwendungen verwendet.

Verarmungslast NMOS

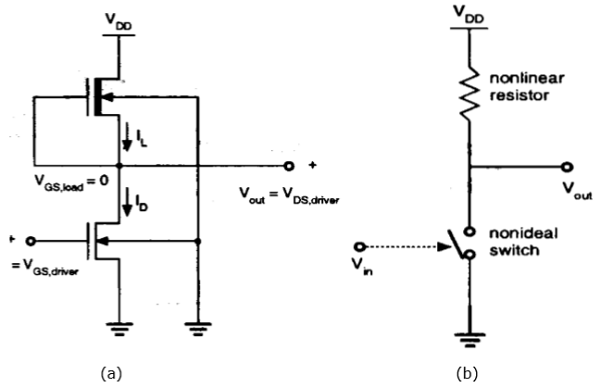
Nachteile des Verbesserungslastwechselrichters können durch Verwendung eines Verarmungslastwechselrichters überwunden werden. Im Vergleich zu einem Wechselrichter mit verbesserter Last erfordert der Wechselrichter mit Verarmungslast einige weitere Herstellungsschritte für das Kanalimplantat, um die Schwellenspannung der Last anzupassen.

Die Vorteile des Verarmungslastwechselrichters sind - scharfer VTC-Übergang, bessere Rauschmarge, einzelne Stromversorgung und kleinerer Gesamtlayoutbereich.

Wie in der Figur gezeigt, sind das Gate und der Source-Anschluss der Last verbunden; Also ist V _GS = 0. Somit ist die Schwellenspannung der Last negativ. Daher,

$$ V_ {GS, load}> V_ {T, load} $$ ist erfüllt

Daher hat das Lastgerät unabhängig vom Eingangs- und Ausgangsspannungspegel immer einen Leitungskanal.

Wenn sich der Lasttransistor im Sättigungsbereich befindet, ist der Laststrom gegeben durch

$$ I_ {D, load} = \ frac {K_ {n, load}} {2} \ left [-V_ {T, load} \ left (V_ {out} \ right) \ right] ^ {2} $ $

Wenn sich der Lasttransistor im linearen Bereich befindet, ist der Laststrom gegeben durch

$$ I_ {D, load} = \ frac {K_ {n, load}} {2} \ left [2 \ left | V_ {T, load} \ left (V_ {out} \ right) \ right |. \ Left (V_ {DD} -V_ {out} \ right) - \ left (V_ {DD} -V_ {out} \ right ) ^ {2} \ right] $$

Die Spannungsübertragungseigenschaften des Verarmungslastwechselrichters sind in der folgenden Abbildung dargestellt.

CMOS-Wechselrichter - Schaltung, Betrieb und Beschreibung

Die CMOS-Inverterschaltung ist in der Abbildung dargestellt. Hier arbeiten nMOS- und pMOS-Transistoren als Treibertransistoren; Wenn ein Transistor eingeschaltet ist, ist der andere ausgeschaltet.

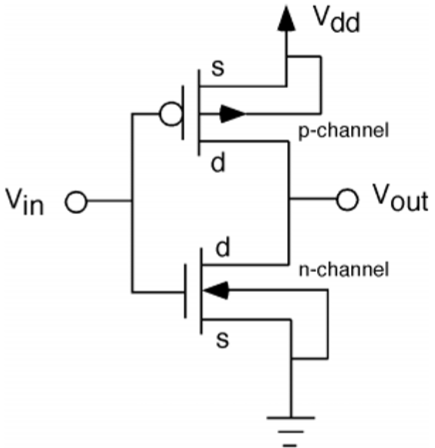
Diese Konfiguration wird aufgerufen complementary MOS (CMOS). Der Eingang ist mit dem Gate-Anschluss beider Transistoren verbunden, so dass beide direkt mit Eingangsspannungen angesteuert werden können. Das Substrat des nMOS ist mit der Erde verbunden, und das Substrat des pMOS ist mit der Stromversorgung V _{DD verbunden} .

Also ist V _SB = 0 für beide Transistoren.

$$ V_ {GS, n} = V_ {in} $$

$$ V_ {DS, n} = V_ {out} $$

Und,

$$ V_ {GS, p} = V_ {in} -V_ {DD} $$

$$ V_ {DS, p} = V_ {out} -V_ {DD} $$

Wenn der Eingang von nMOS kleiner als die Schwellenspannung ist (V _in <V _{TO, n} ), wird der nMOS abgeschaltet und der pMOS befindet sich im linearen Bereich. Der Drainstrom beider Transistoren ist also Null.

$$ I_ {D, n} = I_ {D, p} = 0 $$

Daher ist die Ausgangsspannung V _OH gleich der Versorgungsspannung.

$$ V_ {out} = V_ {OH} = V_ {DD} $$

Wenn die Eingangsspannung größer als V _DD + V _{TO, p ist} , befindet sich der pMOS-Transistor im Grenzbereich und der nMOS im linearen Bereich, so dass der Drainstrom beider Transistoren Null ist.

$$ I_ {D, n} = I_ {D, p} = 0 $$

Daher ist die Ausgangsspannung V _OL gleich Null.

$$ V_ {out} = V_ {OL} = 0 $$

Der nMOS arbeitet im Sättigungsbereich, wenn V _in > V _{TO ist} und wenn die folgenden Bedingungen erfüllt sind.

$$ V_ {DS, n} \ geq V_ {GS, n} -V_ {TO, n} $$

$$ V_ {out} \ geq V_ {in} -V_ {TO, n} $$

Der pMOS arbeitet im Sättigungsbereich, wenn V _in <V _DD + V _{TO, p ist} und wenn die folgenden Bedingungen erfüllt sind.

$$ V_ {DS, p} \ leq V_ {GS, p} -V_ {TO, p} $$

$$ V_ {out} \ leq V_ {in} -V_ {TO, p} $$

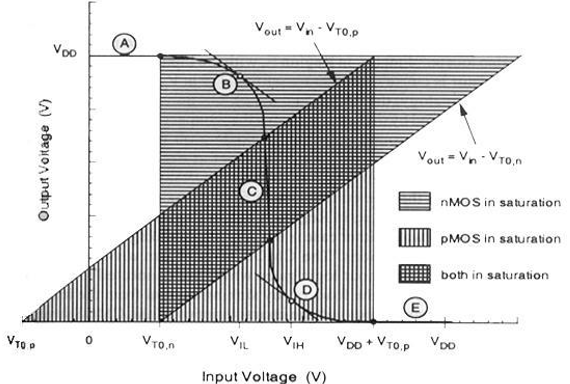
Für unterschiedliche Werte der Eingangsspannungen sind die Betriebsbereiche für beide Transistoren unten aufgeführt.

Region	V in	V raus	nMOS	pMOS
EIN	<V TO, n	V OH	Abgeschnitten	Linear
B.	V IL	Hoch ≈ V OH	Sättigung	Linear
C.	V th	V th	Sättigung	Sättigung
D.	V IH	Niedrig ≈ V OL	Linear	Sättigung
E.	> (V DD + V TO, p )	V OL	Linear	Abgeschnitten

Die VTC von CMOS ist in der folgenden Abbildung dargestellt -