Conexiones de circuito en condensadores
En un circuito, un condensador se puede conectar en serie o en paralelo. Si se conecta un conjunto de condensadores en un circuito, el tipo de conexión de condensador se ocupa de los valores de voltaje y corriente en esa red.
Condensadores en serie
Observemos lo que sucede cuando hay pocos condensadores conectados en serie. Consideremos tres condensadores con diferentes valores, como se muestra en la siguiente figura.

Capacidad
Cuando se considera la capacitancia de una red cuyos capacitores están en serie, se suma el recíproco de las capacitancias de todos los capacitores para obtener el recíproco de la capacitancia total. Para tener esto más claro,
$$ \ frac {1} {C_ {T}} \: \: = \: \: \ frac {1} {C_ {1}} \: \: + \: \: \ frac {1} {C_ { 2}} \: \: + \: \: \ frac {1} {C_ {3}} $$
Siguiendo la misma fórmula, si simplemente dos condensadores están conectados en serie, entonces
$$ C_ {T} \: \: = \: \: \ frac {C_ {1} \: \: \ times \: \: C_ {2}} {C_ {1} \: \: + \: \ : C_ {2}} $$
Donde C 1 es la capacitancia a través de la 1 st condensador, C 2 es la capacitancia a través de la 2 nd condensador y C 3 es la capacitancia a través de la 3 rd condensador en la red anterior.
voltaje
El voltaje en cada capacitor depende del valor de las capacitancias individuales. Lo que significa
$$ V_ {C1} \: \: = \: \: \ frac {Q_ {T}} {C_ {1}} \: \: V_ {C2} \: \: = \: \: \ frac {Q_ {T}} {C_ {2}} \: \: V_ {C3} \: \: = \: \: \ frac {Q_ {T}} {C_ {3}} $$
El voltaje total a través del circuito de condensadores en serie,
$$ V_ {T} \: \: = \: \: V_ {C1} \: \: + \: \: V_ {C2} \: \: + \: \: V_ {C3} $$
Donde V c1 es el voltaje a través de la 1 st condensador, V c2 es el voltaje a través de la 2 nd condensador y V c3 es el voltaje a través de la 3 rd condensador en la red anterior.
Actual
La cantidad total de corriente que fluye a través de un conjunto de condensadores conectados en serie es la misma en todos los puntos. Por lo tanto, los condensadores almacenarán la misma cantidad de carga independientemente de su valor de capacitancia.
Actual a través de la red,
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Donde 1 es la corriente a través de la 1 st condensador, I 2 es la corriente a través de la 2 nd condensador y I 3 es la corriente a través de la 3 rd condensador en la red anterior.
Como la corriente es la misma, el almacenamiento de carga es el mismo porque cualquier placa de un capacitor obtiene su carga del capacitor adyacente y, por lo tanto, los capacitores en serie tendrán la misma carga.
$$ Q_ {T} \: \: = \: \: Q_ {1} \: \: = \: \: Q_ {2} \: \: = \: \: Q_ {3} $$
Condensadores en paralelo
Observemos lo que sucede, cuando se conectan pocos condensadores en paralelo. Consideremos tres condensadores con diferentes valores, como se muestra en la siguiente figura.
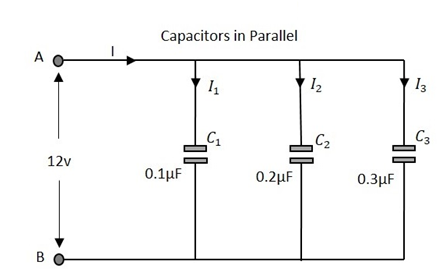
Capacidad
La capacitancia total del circuito es el equivalente a la suma de las capacitancias individuales de los capacitores en la red.
$$ C_ {T} \: \: = \: \: C_ {1} \: \: + \: \: C_ {2} \: \: + \: \: C_ {3} $$
Donde C 1 es la capacitancia a través de la 1 st condensador, C 2 es la capacitancia a través de la 2 nd condensador y C 3 es la capacitancia a través de la 3 rd condensador en la red anterior.
voltaje
El voltaje medido al final del circuito es same como el voltaje en todos los condensadores que están conectados en un circuito paralelo.
$$ V_ {T} \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
Donde V c1 es el voltaje a través de la 1 st condensador, V c2 es el voltaje a través de la 2 nd condensador y V c3 es el voltaje a través de la 3 rd condensador en la red anterior.
Actual
La corriente total que fluye es igual a la suma de las corrientes que fluyen a través de cada condensador conectado en la red en paralelo.
$$ I_ {T} \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Donde 1 es la corriente a través de la 1 st condensador, I 2 es la corriente a través de la 2 nd condensador y I 3 es la corriente a través de la 3 rd condensador en la red anterior.