Conexiones de circuito en resistencias
Una resistencia cuando se conecta en un circuito, esa conexión puede ser en serie o en paralelo. Ahora sepamos qué pasará con los valores totales de corriente, voltaje y resistencia si también están conectados en serie, cuando se conectan en paralelo.
Resistencias en serie
Observemos lo que sucede cuando hay pocas resistencias conectadas en serie. Consideremos tres resistencias con diferentes valores, como se muestra en la siguiente figura.
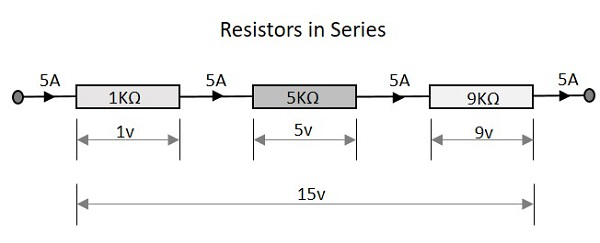
Resistencia
La resistencia total de un circuito que tiene resistencias en serie es igual a la suma de las resistencias individuales. Eso significa que en la figura anterior hay tres resistencias que tienen los valores 1KΩ, 5KΩ y 9KΩ respectivamente.
El valor de resistencia total de la red de resistencias es -
$$ R \: \: = \: \: R_ {1} \: + \: R_ {2} \: + \: R_ {3} $$
Lo que significa que 1 + 5 + 9 = 15KΩ es la resistencia total.
Donde R 1 es la resistencia de la 1ª resistencia, R 2 es la resistencia de la 2ª resistencia y R 3 es la resistencia de la 3ª resistencia en la red de resistencias anterior.
voltaje
El voltaje total que aparece en una red de resistencias en serie es la suma de las caídas de voltaje en cada una de las resistencias individuales. En la figura anterior tenemos tres resistencias diferentes que tienen tres valores diferentes de caídas de voltaje en cada etapa.
Voltaje total que aparece en el circuito -
$$ V \: \: = \: \: V_ {1} \: + \: V_ {2} \: + \: V_ {3} $$
Lo que significa que 1v + 5v + 9v = 15v es el voltaje total.
Donde V 1 es la caída de voltaje de la 1ª resistencia, V 2 es la caída de tensión de la 2ª resistencia y V 3 es la caída de tensión de la 3ª resistencia en la red de resistencias anterior.
Actual
La cantidad total de corriente que fluye a través de un conjunto de resistencias conectadas en serie es la misma en todos los puntos de la red de resistencias. Por lo tanto, la corriente es la misma 5A cuando se mide en la entrada o en cualquier punto entre las resistencias o incluso en la salida.
Actual a través de la red -
$$ I \: \: = \: \: I_ {1} \: = \: I_ {2} \: = \: I_ {3} $$
Lo que significa que la corriente en todos los puntos es 5A.
Donde I 1 es la corriente a través de la 1ª resistencia, I 2 es la corriente a través de la 2ª resistencia e I 3 es la corriente a través de la 3ª resistencia en la red de resistencias anterior.
Resistencias en paralelo
Observemos lo que sucede, cuando pocas resistencias están conectadas en paralelo. Consideremos tres resistencias con diferentes valores, como se muestra en la siguiente figura.
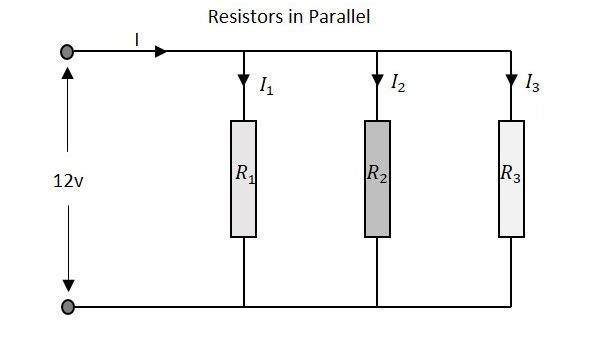
Resistencia
La resistencia total de un circuito que tiene resistencias en paralelo se calcula de manera diferente al método de red de resistencias en serie. Aquí, el valor recíproco (1 / R) de las resistencias individuales se suma con la inversa de la suma algebraica para obtener el valor de resistencia total.
El valor de resistencia total de la red de resistencias es -
$$ \ frac {1} {R} \: \: = \: \: \ frac {1} {R_ {1}} \: \: + \: \: \ frac {1} {R_ {2}} \: \: + \ frac {1} {R_ {3}} $$
Donde R 1 es la resistencia de la 1ª resistencia, R 2 es la resistencia de la 2ª resistencia y R 3 es la resistencia de la 3ª resistencia en la red de resistencias anterior.
Por ejemplo, si se consideran los valores de resistencia del ejemplo anterior, lo que significa R 1 = 1KΩ, R 2 = 5KΩ y R 3 = 9KΩ. La resistencia total de la red de resistencias en paralelo será:
$$ \ frac {1} {R} \: \: = \: \: \ frac {1} {1} \: \: + \: \: \ frac {1} {5} \: \: + \ frac {1} {9} $$
$$ = \: \: \ frac {45 \: \: + \: \: 9 \: \: + \: \: 5} {45} \: \: = \: \: \ frac {59} { 45} $$
$$ R \: \: = \: \: \ frac {45} {59} \: \: = \: \: 0.762K \ Omega \: \: = \: \: 76.2 \ Omega $$
Del método que tenemos para calcular la resistencia en paralelo, podemos derivar una ecuación simple para una red en paralelo de dos resistencias. Es
$$ R \: \: = \: \: \ frac {R_ {1} \: \: \ veces \: \: R_ {2}} {R_ {1} \: \: + \: \: R_ { 2}} \: $$
voltaje
El voltaje total que aparece en una red de resistencias en paralelo es el mismo que las caídas de voltaje en cada resistencia individual.
El voltaje que aparece en el circuito
$$ V \: \: = \: \: V_ {1} \: = \: V_ {2} \: = \: V_ {3} $$
Donde V 1 es la caída de voltaje de la 1ª resistencia, V 2 es la caída de tensión de la 2ª resistencia y V 3 es la caída de tensión de la 3ª resistencia en la red de resistencias anterior. Por tanto, el voltaje es el mismo en todos los puntos de una red de resistencias en paralelo.
Actual
La cantidad total de corriente que ingresa a una red resistiva paralela es la suma de todas las corrientes individuales que fluyen en todas las ramas paralelas. El valor de resistencia de cada rama determina el valor de la corriente que fluye a través de ella. La corriente total a través de la red es
$$ I \: \: = \: \: I_ {1} \: + \: I_ {2} \: + \: I_ {3} $$
Donde I 1 es la corriente a través de la 1ª resistencia, I 2 es la corriente a través de la 2ª resistencia e I 3 es la corriente a través de la 3ª resistencia en la red de resistencias anterior. Por tanto, la suma de las corrientes individuales en diferentes ramas obtiene la corriente total en una red resistiva en paralelo.
Una resistencia se usa particularmente como carga en la salida de muchos circuitos. Si no se usa la carga resistiva, se coloca una resistencia antes de una carga. La resistencia suele ser un componente básico en cualquier circuito.