Conexiones de circuito en inductores
Un inductor cuando se conecta en un circuito, esa conexión puede ser en serie o en paralelo. Ahora sepamos qué pasará con los valores totales de corriente, voltaje y resistencia si también están conectados en serie, cuando se conectan en paralelo.
Inductores en serie
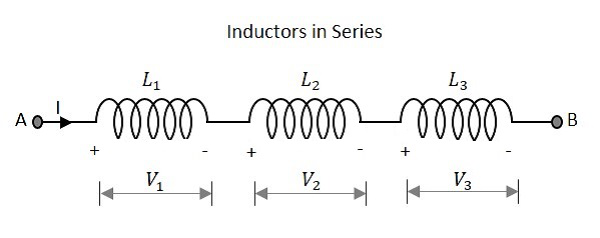
Observemos lo que sucede cuando hay pocos inductores conectados en serie. Consideremos tres resistencias con diferentes valores, como se muestra en la siguiente figura.
Inductancia
La inductancia total de un circuito que tiene inductores en serie es igual a la suma de las inductancias individuales. El valor total de inductancia de la red dada anteriormente es
$$ L_ {T} \: \: = \: \: L_ {1} \: \: + \: \: L_ {2} \: \: + \: \: L_ {3} $$
Donde L 1 es la inductancia de la 1ª resistencia, L 2 es la inductancia de la 2ª resistencia y L 3 es la inductancia de la 3ª resistencia en la red anterior.
voltaje
El voltaje total que aparece en una red de inductores en serie es la suma de caídas de voltaje en cada inductancia individual.
Voltaje total que aparece en el circuito.
$$ V \: \: = \: \: V_ {1} \: \: + \: \: V_ {2} \: \: + \: \: V_ {3} $$
Donde V 1 es la caída de tensión en 1 st inductor, V 2 es la caída de voltaje a través de 2 nd inductor y V 3 es la caída de voltaje a través de 3 rd inductor en la red anterior.
Actual
La cantidad total de corriente que fluye a través de un conjunto de inductores conectados en serie es la misma en todos los puntos de la red.
La corriente a través de la red
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Donde 1 es la corriente a través de la 1 st inductor, I 2 es la corriente a través de la 2 nd inductor y I 3 es la corriente a través de la 3 rd inductor en la red anterior.
Inductores en paralelo
Observemos lo que sucede, cuando pocas resistencias están conectadas en paralelo. Consideremos tres resistencias con diferentes valores, como se muestra en la siguiente figura.

Inductancia
La inductancia total de un circuito que tiene resistencias en paralelo se calcula de manera diferente al método de red de inductores en serie. Aquí, el valor recíproco (1 / R) de las inductancias individuales se agrega con la inversa de la suma algebraica para obtener el valor total de la inductancia.
El valor total de inductancia de la red es
$$ \ frac {1} {L_ {T}} \: \: = \: \: \ frac {1} {L_ {1}} \: \: + \: \: \ frac {1} {L_ { 2}} \: \: + \: \: \ frac {1} {L_ {3}} $$
Donde L 1 es la inductancia de 1 st inductor, L 2 es la inductancia de 2 nd inductor y L 3 es la inductancia de 3 rd inductor en la red anterior.
Del método que tenemos para calcular la inductancia en paralelo, podemos derivar una ecuación simple para una red en paralelo de dos inductores. Es
$$ L_ {T} \: \: = \: \: \ frac {L_ {1} \: \: \ times \: \: L_ {2}} {L_ {1} \: \: + \: \ : L_ {2}} $$
voltaje
El voltaje total que aparece en una red de inductores en paralelo es el mismo que las caídas de voltaje en cada inductancia individual.
El voltaje que aparece en el circuito.
$$ V \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
Donde V 1 es la caída de tensión en 1 st inductor, V 2 es la caída de voltaje a través de 2 nd inductor y V 3 es la caída de voltaje a través de 3 rd inductor en la red anterior. Por tanto, el voltaje es el mismo en todos los puntos de una red de inductores en paralelo.
Actual
La cantidad total de corriente que ingresa a una red inductiva paralela es la suma de todas las corrientes individuales que fluyen en todas las ramas paralelas. El valor de inductancia de cada rama determina el valor de la corriente que fluye a través de ella.
La corriente total a través de la red es
$$ I \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Donde 1 es la corriente a través de la 1 st inductor, I 2 es la corriente a través de la 2 nd inductor y I 3 es la corriente a través de la 3 rd inductor en la red anterior.
Por tanto, la suma de las corrientes individuales en diferentes ramas obtiene la corriente total en una red en paralelo.
Reactancia inductiva
La reactancia inductiva es la oposición que ofrece un inductor al flujo de corriente alterna, o simplemente corriente alterna. Un inductor tiene la propiedad de resistir el cambio en el flujo de corriente y, por lo tanto, muestra cierta oposición que puede denominarse comoreactance, ya que la frecuencia de la corriente de entrada también debe considerarse junto con la resistencia que ofrece.
Indicación - XL
Unidades - Ohms
Símbolo - Ω
En un circuito puramente inductivo, la corriente IL lagsla tensión aplicada en 90 °. La reactancia inductiva se calcula mediante,
$$ X_ {L} \: \: = \: \: 2 \ pi fL $$
Donde f es la frecuencia de la señal. Por tanto, la reactancia inductiva es función de la frecuencia y la inductancia.