Electrónica básica: inductancia
La propiedad de un inductor para obtener el voltaje inducido por el cambio de flujo de corriente se define como inductancia. La inductancia es la relación entre el voltaje y la tasa de cambio de la corriente.
La tasa de cambio de la corriente produce un cambio en el campo magnético, que induce un EMF en dirección opuesta a la fuente de voltaje. Esta propiedad de inducción de EMF se denomina comoInductance.
La fórmula de la inductancia es
$$ Inductancia \: \: = \: \: \ frac {volatge} {tasa \: de \: cambio \: de \: actual} $$
Units −
La unidad de inductancia es Henry. Está indicado porL.
Los inductores están disponibles principalmente en mH (mili Henry) y μH (micro Henry).
Se dice que una bobina tiene una inductancia de one Henry cuando un EMF de one volt se autoinduce en la bobina donde la corriente que fluye cambia a una velocidad de one ampere per second.
Autoinductancia
Si se considera una bobina en la que fluye algo de corriente, tiene algún campo magnético, perpendicular al flujo de corriente. Cuando esta corriente sigue variando, el campo magnético también cambia y este campo magnético cambiante induce un EMF, opuesto al voltaje de la fuente. Este EMF opuesto producido es elself-induced voltage y este método se llama como self-inductance.
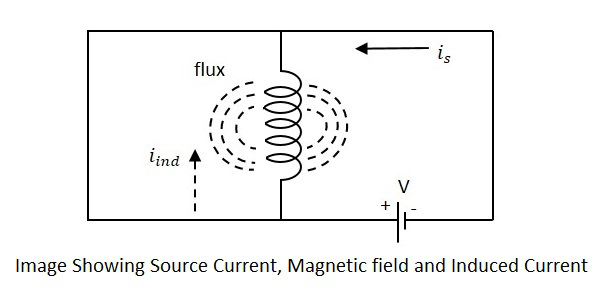
La corriente is en la figura indique la fuente de corriente mientras iindindica la corriente inducida. El flujo representa el flujo magnético creado alrededor de la bobina. Con la aplicación de voltaje, la corrienteisse crean flujos y flujo. Cuando la corrienteis varía, el flujo se vuelve variado produciendo iind.
Este EMF inducido a través de la bobina es proporcional a la tasa de cambio en la corriente. Cuanto mayor sea la tasa de cambio en la corriente, mayor será el valor de EMF inducido.
Podemos escribir la ecuación anterior como
$$ E \: \: \ alpha \: \: \ frac {dI} {dt} $$
$$ E \: \: = \: \: L \: \: \ frac {dI} {dt} $$
Dónde,
E es el EMF producido
dI/dt indica la tasa de cambio de la corriente
L indica el coeficiente de inductancia.
La autoinductancia o coeficiente de autoinducción se puede denominar como
$$ L \: \: = \: \: \ frac {E} {\ frac {dI} {dt}} $$
La ecuación real se escribe como
$$ E \: \: = \: \: - L \: \: \ frac {dI} {dt} $$
El menos en la ecuación anterior indica que the EMF is induced in opposite direction to the voltage source según la ley de Lenz.
Inductancia mutua
Como la bobina portadora de corriente produce algún campo magnético a su alrededor, si se acerca otra bobina a esta bobina, de modo que esté en la región de flujo magnético del primario, entonces el flujo magnético variable induce un EMF en la segunda bobina. Si esta primera bobina se llama comoPrimary coil, el segundo se puede llamar como Secondary coil.
Cuando se induce el EMF en la bobina secundaria debido al campo magnético variable de la bobina primaria, este fenómeno se denomina como Mutual Inductance.
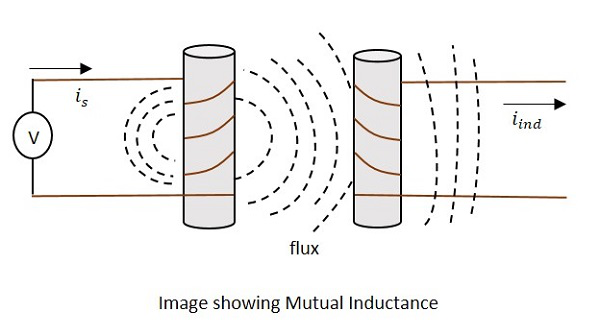
La corriente is en la figura indique la fuente de corriente mientras iindindica la corriente inducida. El flujo representa el flujo magnético creado alrededor de la bobina. Esto también se extiende a la bobina secundaria.
Con la aplicación de voltaje, la corriente isse crean flujos y flujo. Cuando la corrienteis varía, el flujo se vuelve variado produciendo iind en la bobina secundaria, debido a la propiedad de inductancia mutua.
El cambio se produjo así.
$$ V_ {p} \: \: I_ {p} \ rightarrow \: \: B \: \: \ rightarrow \: \: V_ {s} \: \: I_ {s} $$
Dónde,
Vp ip Indique el voltaje y la corriente en la bobina primaria respectivamente
B Indica flujo magnético
Vs is Indique el voltaje y la corriente en la bobina secundaria respectivamente
Inductancia mutua M de los dos circuitos describe la cantidad de voltaje en el secundario inducido por los cambios en la corriente del primario.
$$ V (secundario) \: \: = \: \: - M \ frac {\ Delta I} {\ Delta t} $$
Donde $ \ frac {\ Delta I} {\ Delta t} $ la tasa de cambio de la corriente con el tiempo y Mes el coeficiente de inductancia mutua. El signo menos indica que la dirección de la corriente es opuesta a la fuente.
Units −
Las unidades de inductancia mutua son
$$ voltio \: \: = \: \: M \ frac {amps} {seg} $$
(De la ecuación anterior)
$$ M \: \: = \: \: \ frac {volt. \: Sec} {amp} $$
$$ = \: \: Henry (H) $$
Dependiendo del número de vueltas de las bobinas primaria y secundaria, varía el enlace de flujo magnético y la cantidad de EMF inducida. El número de vueltas en el primario se indica con N1 y el secundario con N2. El coeficiente de acoplamiento es el término que especifica la inductancia mutua de las dos bobinas.
Factores que afectan la inductancia
Hay algunos factores que afectan el rendimiento de un inductor. Los principales se analizan a continuación.
Longitud de la bobina
La longitud de la bobina inductora es inversamente proporcional a la inductancia de la bobina. Si la longitud de la bobina es mayor, la inductancia ofrecida por ese inductor es menor y viceversa.
Área de sección transversal de la bobina
El área de la sección transversal de la bobina es directamente proporcional a la inductancia de la bobina. Cuanto mayor sea el área de la bobina, mayor será la inductancia.
Número de vueltas
Con el número de vueltas, la bobina afecta directamente a la inductancia. El valor de la inductancia se cuadra con el número de vueltas que tiene la bobina. Por lo tanto, cuanto mayor sea el número de vueltas, el cuadrado será el valor de inductancia de la bobina.
Permeabilidad del núcleo
los permeability (μ)del material del núcleo del inductor indica el soporte que proporciona el núcleo para la formación de un campo magnético dentro de sí mismo. loshigher la permeabilidad del material del núcleo, la higher será la inductancia.
Coeficiente de acoplamiento
Este es un factor importante que debe conocerse para calcular la inductancia mutua de dos bobinas. Consideremos dos bobinas cercanas de vueltas N1 y N2 respectivamente.
La corriente a través de la primera bobina i 1 produce un flujo Ψ 1 . La cantidad de enlaces de flujo magnético se entiende por weber-turn.
Deje que la cantidad de enlace de flujo magnético a la segunda bobina, debido a la unidad actual de i 1 sea
$$ \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Esto puede entenderse como el coeficiente de inductancia mutua, que significa
$$ M \: \: = \: \: \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Por lo tanto, el coeficiente de inductancia mutua entre dos bobinas o circuitos se entiende como las vueltas de Weber en una bobina debido a 1A de corriente en la otra bobina.
Si la autoinductancia de la primera bobina es L 1 , entonces
$$ L_ {1} i_ {1} \: \: = \: \: {N_ {1} \ varphi_ {1}} \: \: => \: \: \ frac {L_ {1}} {N_ {1}} \: \: \ frac {\ varphi_ {1}} {i_ {1}} $$
$$ M \: \: = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} $$
De manera similar, el coeficiente de inductancia mutua debido a la corriente i 2 en la segunda bobina es
$$ M \: \: = \: \: \ frac {N_ {1} \ varphi_ {2}} {i_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \ : 1 $$
Si la autoinductancia de la segunda bobina es L 2
$$ L_ {2} i_ {2} \: \: = \: \: N_ {2} \ varphi_ {2} $$
$$ \ frac {L_ {2}} {N_ {2}} \: \: = \: \: \ frac {\ varphi_ {2}} {i_ {2}} $$
Por lo tanto,
$$ M \: \: = \: \: \ frac {N_ {1} L_ {2}} {N_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \: 2 $$
Multiplicando 1 y 2, obtenemos
$$ M \: \: \ times \: \: M = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} \: \: \ times \: \: \ frac { N_ {1} L_ {2}} {N_ {2}} $$
$$ M ^ {2} \: \: = \: \: L_ {1} L_ {2} \: \: => \: \: M \: \: = \: \: \ sqrt {L_ {1 } L_ {2}} $$
La ecuación anterior es válida cuando todo el flujo cambiante de la bobina primaria se enlaza con la bobina secundaria, que es un caso ideal. Pero en la práctica, no es el caso. Por tanto, podemos escribir como
$$ M \: \: \ neq \: \: \ sqrt {L_ {1} L_ {2}} $$
$$ y \ frac {M} {\ sqrt {L_ {1} L_ {2}}} \: \: = \: \: K \: \: \ neq \: \: 1 $$
Donde K se conoce como coeficiente de acoplamiento.
los Coefficient of coupling K se puede definir como la relación entre el coeficiente real de inductancia mutua y el coeficiente ideal (máximo) de inductancia mutua.
Si el valor de k está cerca de la unidad, entonces se dice que las bobinas están estrechamente acopladas y si el valor de k = 0, entonces se dice que las bobinas están débilmente acopladas.
Aplicaciones de inductores
Hay muchas aplicaciones de los inductores, como:
Los inductores se utilizan en circuitos de filtro para detectar componentes de alta frecuencia y suprimir señales de ruido.
Para aislar el circuito de señales de HF no deseadas.
Los inductores se utilizan en circuitos eléctricos para formar un transformador y aislar los circuitos de los picos.
Los inductores también se utilizan en motores.