Varios métodos de clasificación

Aquí discutiremos otros métodos de clasificación como los algoritmos genéticos, el enfoque de conjunto aproximado y el enfoque de conjunto difuso.

Algoritmos genéticos

La idea de algoritmo genético se deriva de la evolución natural. En el algoritmo genético, en primer lugar, se crea la población inicial. Esta población inicial consta de reglas generadas aleatoriamente. Podemos representar cada regla mediante una cadena de bits.

Por ejemplo, en un conjunto de entrenamiento dado, las muestras se describen mediante dos atributos booleanos como A1 y A2. Y este conjunto de entrenamiento dado contiene dos clases como C1 y C2.

Podemos codificar la regla IF A1 AND NOT A2 THEN C2 en una cadena de bits 100. En esta representación de bits, los dos bits más a la izquierda representan el atributo A1 y A2, respectivamente.

Asimismo, la regla IF NOT A1 AND NOT A2 THEN C1 se puede codificar como 001.

Note- Si el atributo tiene valores K donde K> 2, entonces podemos usar los bits K para codificar los valores del atributo. Las clases también se codifican de la misma manera.

Puntos para recordar -

Con base en la noción de la supervivencia del más apto, se forma una nueva población que consta de las reglas más aptas en la población actual y los valores de descendencia de estas reglas también.
La idoneidad de una regla se evalúa mediante la precisión de su clasificación en un conjunto de muestras de entrenamiento.
Los operadores genéticos como el cruce y la mutación se aplican para crear descendencia.
En el cruce, la subcadena de un par de reglas se intercambia para formar un nuevo par de reglas.
En la mutación, los bits seleccionados al azar en la cadena de una regla se invierten.

Enfoque de conjunto aproximado

Podemos utilizar el enfoque de conjunto aproximado para descubrir la relación estructural dentro de datos imprecisos y ruidosos.

Note- Este enfoque solo se puede aplicar a atributos de valor discreto. Por lo tanto, los atributos de valor continuo deben discretizarse antes de su uso.

La teoría de conjuntos aproximados se basa en el establecimiento de clases de equivalencia dentro de los datos de entrenamiento dados. Las tuplas que forman la clase de equivalencia son indiscernibles. Significa que las muestras son idénticas con respecto a los atributos que describen los datos.

Hay algunas clases en los datos del mundo real dados, que no se pueden distinguir en términos de atributos disponibles. Podemos usar los conjuntos aproximados pararoughly definir tales clases.

Para una clase C dada, la definición de conjunto aproximada se aproxima por dos conjuntos de la siguiente manera:

Lower Approximation of C - La aproximación inferior de C consta de todas las tuplas de datos que, según el conocimiento del atributo, seguramente pertenecerán a la clase C.
Upper Approximation of C - La aproximación superior de C está formada por todas las tuplas, que con base en el conocimiento de los atributos, no pueden describirse como no pertenecientes a C.

El siguiente diagrama muestra la aproximación superior e inferior de la clase C -

Enfoques de conjuntos difusos

La teoría de conjuntos difusos también se denomina teoría de la posibilidad. Esta teoría fue propuesta por Lotfi Zadeh en 1965 como alternativa a latwo-value logic y probability theory. Esta teoría nos permite trabajar con un alto nivel de abstracción. También nos proporciona los medios para lidiar con la medición imprecisa de datos.

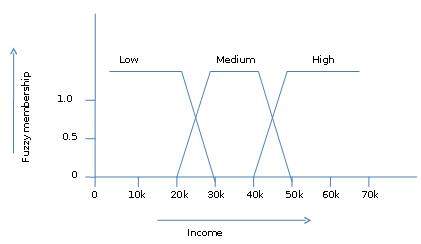
La teoría de conjuntos difusos también nos permite tratar con hechos vagos o inexactos. Por ejemplo, ser miembro de un conjunto de altos ingresos es exacto (por ejemplo, si $ 50 000 es alto, entonces, ¿qué pasa con $ 49 000 y $ 48 000)? A diferencia del conjunto CRISP tradicional, donde el elemento pertenece a S o su complemento, pero en la teoría de conjuntos difusos, el elemento puede pertenecer a más de un conjunto difuso.

Por ejemplo, el valor de los ingresos $ 49 000 pertenece a los conjuntos difusos medio y alto, pero en grados diferentes. La notación de conjuntos difusos para este valor de ingresos es la siguiente:

m_{medium_income}($49k)=0.15 and m_{high_income}($49k)=0.96

donde 'm' es la función de pertenencia que opera en los conjuntos difusos de ingreso_medio y ingreso_alto respectivamente. Esta notación se puede mostrar en forma de diagrama de la siguiente manera: