Big Data Analytics - Analyse des séries chronologiques
Les séries chronologiques sont une séquence d'observations de variables catégorielles ou numériques indexées par une date ou un horodatage. Un exemple clair de données de séries chronologiques est la série chronologique du cours d'une action. Dans le tableau suivant, nous pouvons voir la structure de base des données de séries chronologiques. Dans ce cas, les observations sont enregistrées toutes les heures.
| Horodatage | Prix de l'action |
|---|---|
| 11/10/2015 09:00:00 | 100 |
| 11/10/2015 10:00:00 | 110 |
| 11/10/2015 11:00:00 | 105 |
| 11/10/2015 12:00:00 | 90 |
| 11/10/2015 13:00:00 | 120 |
Normalement, la première étape de l'analyse des séries chronologiques consiste à tracer la série, cela se fait normalement avec un graphique linéaire.
L'application la plus courante de l'analyse des séries chronologiques consiste à prévoir les valeurs futures d'une valeur numérique à l'aide de la structure temporelle des données. Cela signifie que les observations disponibles sont utilisées pour prédire les valeurs du futur.
L'ordre temporel des données implique que les méthodes de régression traditionnelles ne sont pas utiles. Afin de construire des prévisions robustes, nous avons besoin de modèles qui prennent en compte l'ordre temporel des données.
Le modèle le plus largement utilisé pour l'analyse des séries chronologiques est appelé Autoregressive Moving Average(ARMA). Le modèle se compose de deux parties, unautoregressive (AR) et un moving average(MA) partie. Le modèle est alors généralement appelé le modèle ARMA (p, q) où p est l'ordre de la partie autorégressive et q est l'ordre de la partie moyenne mobile.
Modèle autorégressif
L' AR (p) se lit comme un modèle autorégressif d'ordre p. Mathématiquement, il s'écrit -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
où {φ 1 ,…, φ p } sont des paramètres à estimer, c est une constante et la variable aléatoire ε t représente le bruit blanc. Certaines contraintes sont nécessaires sur les valeurs des paramètres pour que le modèle reste stationnaire.
Moyenne mobile
La notation MA (q) fait référence au modèle de moyenne mobile d'ordre q -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
où les θ 1 , ..., θ q sont les paramètres du modèle, μ est l'espérance de X t , et les ε t , ε t - 1 , ... sont des termes d'erreur de bruit blanc.
Moyenne mobile autorégressive
Le modèle ARMA (p, q) combine p termes autorégressifs et q termes de moyenne mobile. Mathématiquement, le modèle est exprimé avec la formule suivante -
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
Nous pouvons voir que le modèle ARMA (p, q) est une combinaison de modèles AR (p) et MA (q) .
Pour donner une certaine intuition du modèle, considérons que la partie AR de l'équation cherche à estimer des paramètres pour X t - i observations de afin de prédire la valeur de la variable dans X t . Il s'agit au final d'une moyenne pondérée des valeurs passées. La section MA utilise la même approche mais avec l'erreur des observations précédentes, ε t - i . Donc au final, le résultat du modèle est une moyenne pondérée.
L'extrait de code suivant montre comment mettre en œuvre un ARMA (p, q) dans R .
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
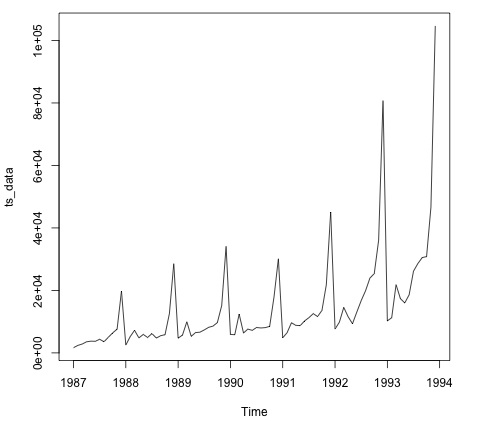
plot.ts(ts_data)Le traçage des données est normalement la première étape pour savoir s'il existe une structure temporelle dans les données. Nous pouvons voir sur le graphique qu'il y a de fortes pointes à la fin de chaque année.
Le code suivant adapte un modèle ARMA aux données. Il exécute plusieurs combinaisons de modèles et sélectionne celui qui a le moins d'erreur.
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172