Systèmes de contrôle - Réduction du schéma fonctionnel
Les concepts abordés dans le chapitre précédent sont utiles pour réduire (simplifier) les schémas fonctionnels.
Règles de réduction des schémas fonctionnels
Suivez ces règles pour simplifier (réduire) le diagramme, qui comporte de nombreux blocs, points de sommation et points de décollage.
Rule 1 - Vérifier les blocs connectés en série et simplifier.
Rule 2 - Vérifier les blocs connectés en parallèle et simplifier.
Rule 3 - Vérifier les blocs connectés en boucle de rétroaction et simplifier.
Rule 4 - En cas de difficulté avec le point de décollage lors de la simplification, déplacez-le vers la droite.
Rule 5 - En cas de difficulté avec le point de sommation lors de la simplification, déplacez-le vers la gauche.
Rule 6 - Répétez les étapes ci-dessus jusqu'à ce que vous obteniez le formulaire simplifié, c'est-à-dire un seul bloc.
Note - La fonction de transfert présente dans ce bloc unique est la fonction de transfert du schéma de principe global.
Exemple
Considérez le schéma fonctionnel présenté dans la figure suivante. Simplifions (réduisons) ce diagramme en utilisant les règles de réduction du diagramme en bloc.

Step 1- Utilisez la règle 1 pour les blocs $ G_1 $ et $ G_2 $. Utilisez la règle 2 pour les blocs $ G_3 $ et $ G_4 $. Le schéma fonctionnel modifié est illustré dans la figure suivante.

Step 2- Utilisez la règle 3 pour les blocs $ G_1G_2 $ et $ H_1 $. Utilisez la règle 4 pour changer le point de décollage après le bloc $ G_5 $. Le schéma fonctionnel modifié est illustré dans la figure suivante.

Step 3- Utilisez la règle 1 pour les blocs $ (G_3 + G_4) $ et $ G_5 $. Le schéma fonctionnel modifié est illustré dans la figure suivante.

Step 4- Utilisez la règle 3 pour les blocs $ (G_3 + G_4) G_5 $ et $ H_3 $. Le schéma fonctionnel modifié est illustré dans la figure suivante.

Step 5- Utilisez la règle 1 pour les blocs connectés en série. Le schéma fonctionnel modifié est illustré dans la figure suivante.

Step 6- Utilisez la règle 3 pour les blocs connectés en boucle de rétroaction. Le schéma fonctionnel modifié est illustré dans la figure suivante. Ceci est le schéma fonctionnel simplifié.
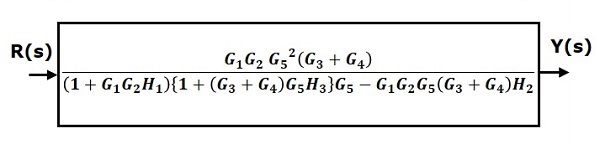
Par conséquent, la fonction de transfert du système est
$$ \ frac {Y (s)} {R (s)} = \ frac {G_1G_2G_5 ^ 2 (G_3 + G_4)} {(1 + G_1G_2H_1) \ lbrace 1+ (G_3 + G_4) G_5H_3 \ rbrace G_5-G_1G_2G_5 (G_3 + G_4) H_2} $$
Note - Suivez ces étapes pour calculer la fonction de transfert du diagramme à plusieurs entrées.
Step 1 - Trouvez la fonction de transfert du diagramme en considérant une entrée à la fois et mettez les entrées restantes à zéro.
Step 2 - Répétez l'étape 1 pour les entrées restantes.
Step 3 - Obtenez la fonction de transfert globale en ajoutant toutes ces fonctions de transfert.
Le processus de réduction du schéma fonctionnel prend plus de temps pour les systèmes complexes. Parce que nous devons dessiner le diagramme (partiellement simplifié) après chaque étape. Donc, pour surmonter cet inconvénient, utilisez des graphiques de flux de signaux (représentation).
Dans les deux chapitres suivants, nous discuterons des concepts liés aux graphiques de flux de signaux, c'est-à-dire comment représenter un graphique de flux de signaux à partir d'un schéma de principe donné et le calcul de la fonction de transfert simplement en utilisant une formule de gain sans effectuer de processus de réduction.