Systèmes de contrôle - Guide rapide
Un système de contrôle est un système qui fournit la réponse souhaitée en contrôlant la sortie. La figure suivante montre le schéma de principe simple d'un système de commande.

Ici, le système de contrôle est représenté par un seul bloc. Depuis, la sortie est contrôlée par l'entrée variable, le système de contrôle a obtenu ce nom. Nous varierons cette entrée avec un mécanisme. Dans la section suivante sur les systèmes de contrôle en boucle ouverte et en boucle fermée, nous étudierons en détail les blocs à l'intérieur du système de contrôle et comment faire varier cette entrée afin d'obtenir la réponse souhaitée.
Examples - Système de contrôle des feux de circulation, machine à laver
Traffic lights control systemest un exemple de système de contrôle. Ici, une séquence de signal d'entrée est appliquée à ce système de commande et la sortie est l'une des trois lumières qui seront allumées pendant un certain temps. Pendant ce temps, les deux autres lumières seront éteintes. Sur la base de l'étude du trafic à un carrefour particulier, les heures d'allumage et d'extinction des feux peuvent être déterminées. En conséquence, le signal d'entrée contrôle la sortie. Ainsi, le système de contrôle des feux de signalisation fonctionne en fonction du temps.
Classification des systèmes de contrôle
Sur la base de certains paramètres, nous pouvons classer les systèmes de contrôle de la manière suivante.
Systèmes de contrôle à temps continu et à temps discret
Les systèmes de contrôle peuvent être classés comme des systèmes de contrôle du temps continu et des systèmes de contrôle du temps discret basés sur le type of the signal utilisé.
Dans continuous timesystèmes de contrôle, tous les signaux sont continus dans le temps. Mais endiscrete time systèmes de contrôle, il existe un ou plusieurs signaux horaires discrets.
Systèmes de contrôle SISO et MIMO
Les systèmes de contrôle peuvent être classés comme systèmes de contrôle SISO et systèmes de contrôle MIMO basés sur number of inputs and outputs présent.
SISOLes systèmes de contrôle (entrée unique et sortie unique) ont une entrée et une sortie. Tandis que,MIMO Les systèmes de contrôle (entrées multiples et sorties multiples) ont plus d'une entrée et plus d'une sortie.
Systèmes de contrôle en boucle ouverte et en boucle fermée
Les systèmes de contrôle peuvent être classés comme systèmes de contrôle en boucle ouverte et systèmes de contrôle en boucle fermée basés sur feedback path.
Dans open loop control systems, la sortie n'est pas renvoyée à l'entrée. Ainsi, l'action de contrôle est indépendante de la sortie souhaitée.
La figure suivante montre le schéma de principe du système de commande en boucle ouverte.

Ici, une entrée est appliquée à un contrôleur et produit un signal d'actionnement ou un signal de commande. Ce signal est donné en tant qu'entrée d'une installation ou d'un processus à contrôler. Ainsi, l'usine produit une sortie, qui est contrôlée. Le système de contrôle des feux de signalisation dont nous avons discuté précédemment est un exemple de système de contrôle en boucle ouverte.
Dans closed loop control systems, la sortie est renvoyée à l'entrée. Ainsi, l'action de contrôle dépend de la sortie souhaitée.
La figure suivante montre le schéma fonctionnel du système de contrôle en boucle fermée à rétroaction négative.
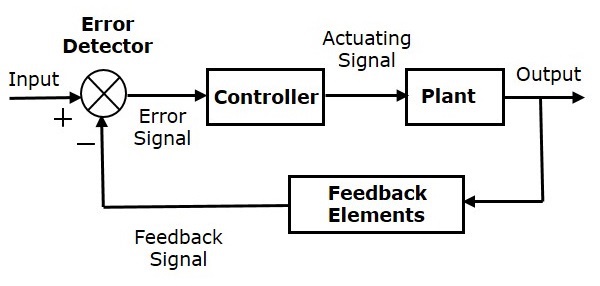
Le détecteur d'erreur produit un signal d'erreur, qui est la différence entre l'entrée et le signal de retour. Ce signal de retour est obtenu à partir du bloc (éléments de retour) en considérant la sortie du système global comme une entrée de ce bloc. Au lieu de l'entrée directe, le signal d'erreur est appliqué en tant qu'entrée à un contrôleur.
Ainsi, le contrôleur produit un signal d'actionnement qui commande l'installation. Dans cette combinaison, la sortie du système de contrôle est ajustée automatiquement jusqu'à ce que nous obtenions la réponse souhaitée. Par conséquent, les systèmes de contrôle en boucle fermée sont également appelés les systèmes de contrôle automatique. Le système de contrôle des feux de signalisation ayant un capteur à l'entrée est un exemple de système de contrôle en boucle fermée.
Les différences entre les systèmes de contrôle en boucle ouverte et en boucle fermée sont mentionnées dans le tableau suivant.
| Systèmes de contrôle en boucle ouverte | Systèmes de contrôle en boucle fermée |
|---|---|
| L'action de contrôle est indépendante de la sortie souhaitée. | L'action de contrôle dépend de la sortie souhaitée. |
| Le chemin de rétroaction n'est pas présent. | Un chemin de rétroaction est présent. |
| Ceux-ci sont également appelés comme non-feedback control systems. | Ceux-ci sont également appelés comme feedback control systems. |
| Conception simple. | Difficile à concevoir. |
| Ce sont économiques. | Celles-ci sont plus coûteuses. |
| Inexacte. | Précis. |
Si la sortie ou une partie de la sortie est renvoyée vers l'entrée et utilisée comme partie de l'entrée système, on parle alors de feedback. Le feedback joue un rôle important pour améliorer les performances des systèmes de contrôle. Dans ce chapitre, laissez-nous discuter des types de rétroaction et des effets de la rétroaction.
Types de rétroaction
Il existe deux types de commentaires -
- Commentaire positif
- Retours négatifs
Commentaire positif
La rétroaction positive ajoute l'entrée de référence, $R(s)$et sortie de rétroaction. La figure suivante montre le schéma de principe depositive feedback control system.

Le concept de fonction de transfert sera discuté dans les chapitres suivants. Pour le moment, considérez que la fonction de transfert du système de contrôle à rétroaction positive est,
$T=\frac{G}{1-GH}$ (Équation 1)
Où,
T est la fonction de transfert ou le gain global du système de contrôle à rétroaction positive.
G est le gain en boucle ouverte, qui est fonction de la fréquence.
H est le gain du chemin de rétroaction, qui est fonction de la fréquence.
Retours négatifs
Un retour négatif réduit l'erreur entre l'entrée de référence, $R(s)$et la sortie du système. La figure suivante montre le schéma de principe dunegative feedback control system.

La fonction de transfert du système de contrôle de rétroaction négative est,
$T=\frac{G}{1+GH}$ (Équation 2)
Où,
T est la fonction de transfert ou le gain global du système de contrôle à rétroaction négative.
G est le gain en boucle ouverte, qui est fonction de la fréquence.
H est le gain du chemin de rétroaction, qui est fonction de la fréquence.
La dérivation de la fonction de transfert ci-dessus est présentée dans les chapitres suivants.
Effets de la rétroaction
Comprenons maintenant les effets du feedback.
Effet de la rétroaction sur le gain global
À partir de l'équation 2, nous pouvons dire que le gain global du système de contrôle en boucle fermée à rétroaction négative est le rapport de «G» et (1 + GH). Ainsi, le gain global peut augmenter ou diminuer en fonction de la valeur de (1 + GH).
Si la valeur de (1 + GH) est inférieure à 1, le gain global augmente. Dans ce cas, la valeur «GH» est négative car le gain du chemin de rétroaction est négatif.
Si la valeur de (1 + GH) est supérieure à 1, le gain global diminue. Dans ce cas, la valeur «GH» est positive car le gain du chemin de rétroaction est positif.
En général, «G» et «H» sont des fonctions de fréquence. Ainsi, la rétroaction augmentera le gain global du système dans une plage de fréquences et diminuera dans l'autre plage de fréquences.
Effet du feedback sur la sensibilité
Sensitivity du gain global du système de contrôle en boucle fermée à rétroaction négative (T) à la variation du gain en boucle ouverte (G) est défini comme
$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{Percentage\: change \: in \:T}{Percentage\: change \: in \:G}$ (Équation 3)
Où, ∂T est le changement incrémentiel de T dû au changement incrémentiel de G.
Nous pouvons réécrire l'équation 3 comme
$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ (Équation 4)
Faites une différenciation partielle par rapport à G des deux côtés de l'équation 2.
$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH).1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ (Équation 5)
À partir de l'équation 2, vous obtiendrez
$\frac{G}{T}=1+GH$ (Équation 6)
Remplacez l'équation 5 et l'équation 6 dans l'équation 4.
$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$
Donc, nous avons le sensitivitydu gain global du système de contrôle en boucle fermée comme l'inverse de (1 + GH). Ainsi, la sensibilité peut augmenter ou diminuer en fonction de la valeur de (1 + GH).
Si la valeur de (1 + GH) est inférieure à 1, la sensibilité augmente. Dans ce cas, la valeur «GH» est négative car le gain du chemin de rétroaction est négatif.
Si la valeur de (1 + GH) est supérieure à 1, la sensibilité diminue. Dans ce cas, la valeur «GH» est positive car le gain du chemin de rétroaction est positif.
En général, «G» et «H» sont des fonctions de fréquence. Ainsi, la rétroaction augmentera la sensibilité du gain du système dans une plage de fréquences et diminuera dans l'autre plage de fréquences. Par conséquent, nous devons choisir les valeurs de «GH» de manière à ce que le système soit insensible ou moins sensible aux variations de paramètres.
Effet de la rétroaction sur la stabilité
Un système est dit stable, si sa sortie est sous contrôle. Sinon, on dit qu'il est instable.
Dans l'équation 2, si la valeur du dénominateur est zéro (c'est-à-dire GH = -1), alors la sortie du système de contrôle sera infinie. Ainsi, le système de contrôle devient instable.
Par conséquent, nous devons bien choisir le retour d'information afin de rendre le système de contrôle stable.
Effet de la rétroaction sur le bruit
Pour connaître l'effet de la rétroaction sur le bruit, comparons les relations de fonction de transfert avec et sans rétroaction due au seul signal de bruit.
Considérez un open loop control system avec un signal de bruit comme indiqué ci-dessous.

le open loop transfer function en raison du seul signal de bruit
$\frac{C(s)}{N(s)}=G_b$ (Équation 7)
Il s'obtient en faisant l'autre entrée $R(s)$ égal à zéro.
Considérez un closed loop control system avec un signal de bruit comme indiqué ci-dessous.

le closed loop transfer function en raison du seul signal de bruit
$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ (Équation 8)
Il s'obtient en faisant l'autre entrée $R(s)$ égal à zéro.
Comparez l'équation 7 et l'équation 8,
Dans le système de commande en boucle fermée, le gain dû au signal de bruit est diminué d'un facteur de $(1+G_a G_b H)$ à condition que le terme $(1+G_a G_b H)$ est supérieur à un.
Les systèmes de contrôle peuvent être représentés avec un ensemble d'équations mathématiques appelées mathematical model. Ces modèles sont utiles pour l'analyse et la conception de systèmes de contrôle. L'analyse du système de contrôle signifie trouver la sortie lorsque nous connaissons l'entrée et le modèle mathématique. La conception du système de contrôle signifie trouver le modèle mathématique lorsque nous connaissons l'entrée et la sortie.
Les modèles mathématiques suivants sont principalement utilisés.
- Modèle d'équation différentielle
- Modèle de fonction de transfert
- Modèle d'espace d'état
Discutons des deux premiers modèles dans ce chapitre.
Modèle d'équation différentielle
Le modèle d'équation différentielle est un modèle mathématique du domaine temporel des systèmes de contrôle. Suivez ces étapes pour le modèle d'équation différentielle.
Appliquer les lois de base au système de contrôle donné.
Obtenez l'équation différentielle en termes d'entrée et de sortie en éliminant la ou les variables intermédiaires.
Exemple
Tenez compte du système électrique suivant, comme illustré dans la figure suivante. Ce circuit se compose d'une résistance, d'une inductance et d'un condensateur. Tous ces éléments électriques sont connectés enseries. La tension d'entrée appliquée à ce circuit est$v_i$ et la tension aux bornes du condensateur est la tension de sortie $v_o$.

L'équation de maillage pour ce circuit est
$$v_i=Ri+L\frac{\text{d}i}{\text{d}t}+v_o$$
Substitut, le courant passant à travers le condensateur $i=c\frac{\text{d}v_o}{\text{d}t}$ dans l'équation ci-dessus.
$$\Rightarrow\:v_i=RC\frac{\text{d}v_o}{\text{d}t}+LC\frac{\text{d}^2v_o}{\text{d}t^2}+v_o$$
$$\Rightarrow\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$
L'équation ci-dessus est un second ordre differential equation.
Modèle de fonction de transfert
Le modèle de fonction de transfert est un modèle mathématique du domaine s des systèmes de contrôle. leTransfer function d'un système LTI (Linear Time Invariant) est défini comme le rapport entre la transformée de Laplace de la sortie et la transformée de Laplace de l'entrée en supposant que toutes les conditions initiales sont nulles.
Si $x(t)$ et $y(t)$ sont l'entrée et la sortie d'un système LTI, alors les transformées de Laplace correspondantes sont $X(s)$ et $Y(s)$.
Par conséquent, la fonction de transfert du système LTI est égale au rapport de $Y(s)$ et $X(s)$.
$$i.e.,\: Transfer\: Function =\frac{Y(s)}{X(s)}$$
Le modèle de fonction de transfert d'un système LTI est illustré dans la figure suivante.

Ici, nous avons représenté un système LTI avec un bloc ayant une fonction de transfert à l'intérieur. Et ce bloc a une entrée$X(s)$ & production $Y(s)$.
Exemple
Auparavant, nous obtenions l'équation différentielle d'un système électrique comme
$$\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$
Appliquez la transformation de Laplace des deux côtés.
$$s^2V_o(s)+\left ( \frac{sR}{L} \right )V_o(s)+\left ( \frac{1}{LC} \right )V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$
$$\Rightarrow \left \{ s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC} \right \}V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$
$$\Rightarrow \frac{V_o(s)}{V_i(s)}=\frac{\frac{1}{LC}}{s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC}}$$
Où,
$v_i(s)$ est la transformée de Laplace de la tension d'entrée $v_i$
$v_o(s)$ est la transformée de Laplace de la tension de sortie $v_o$
L'équation ci-dessus est un transfer functiondu système électrique du second ordre. Le modèle de fonction de transfert de ce système est illustré ci-dessous.

Ici, nous montrons un système électrique de second ordre avec un bloc ayant la fonction de transfert à l'intérieur. Et ce bloc a une entrée$V_i(s)$ & une sortie $V_o(s)$.
Dans ce chapitre, parlons de la differential equation modelingdes systèmes mécaniques. Il existe deux types de systèmes mécaniques en fonction du type de mouvement.
- Systèmes mécaniques translationnels
- Systèmes mécaniques rotatifs
Modélisation des systèmes mécaniques translationnels
Les systèmes mécaniques de translation se déplacent straight line. Ces systèmes se composent principalement de trois éléments de base. Ce sont la masse, le ressort et le dashpot ou l'amortisseur.
Si une force est appliquée à un système mécanique de translation, elle est alors opposée par des forces opposées dues à la masse, à l'élasticité et au frottement du système. Puisque la force appliquée et les forces opposées sont dans des directions opposées, la somme algébrique des forces agissant sur le système est nulle. Voyons maintenant la force opposée par ces trois éléments individuellement.
Masse
La masse est la propriété d'un corps qui stocke kinetic energy. Si une force est appliquée sur un corps ayant une masseM, alors il est opposé par une force opposée due à la masse. Cette force opposée est proportionnelle à l'accélération du corps. Supposons que l'élasticité et le frottement soient négligeables.

$$F_m\propto\: a$$
$$\Rightarrow F_m=Ma=M\frac{\text{d}^2x}{\text{d}t^2}$$
$$F=F_m=M\frac{\text{d}^2x}{\text{d}t^2}$$
Où,
F est la force appliquée
Fm est la force opposée due à la masse
M est la masse
a est l'accélération
x est le déplacement
Printemps
Le printemps est un élément qui stocke potential energy. Si une force est appliquée sur le ressortK, alors il est opposé par une force opposée due à l'élasticité du ressort. Cette force opposée est proportionnelle au déplacement du ressort. Supposons que la masse et le frottement sont négligeables.

$$F\propto\: x$$
$$\Rightarrow F_k=Kx$$
$$F=F_k=Kx$$
Où,
F est la force appliquée
Fk est la force opposée due à l'élasticité du ressort
K est la constante du ressort
x est le déplacement
Dashpot
Si une force est appliquée sur le dashpot B, alors il est opposé par une force opposée due à frictiondu dashpot. Cette force opposée est proportionnelle à la vitesse du corps. Supposons que la masse et l'élasticité soient négligeables.

$$F_b\propto\: \nu$$
$$\Rightarrow F_b=B\nu=B\frac{\text{d}x}{\text{d}t}$$
$$F=F_b=B\frac{\text{d}x}{\text{d}t}$$
Où,
Fb est la force opposée due au frottement du dashpot
B est le coefficient de frottement
v est la vitesse
x est le déplacement
Modélisation des systèmes mécaniques de rotation
Les systèmes mécaniques de rotation se déplacent autour d'un axe fixe. Ces systèmes se composent principalement de trois éléments de base. Ce sontmoment of inertia, torsional spring et dashpot.
Si un couple est appliqué à un système mécanique en rotation, il est alors opposé par des couples opposés dus au moment d'inertie, à l'élasticité et au frottement du système. Le couple appliqué et les couples opposés étant dans des sens opposés, la somme algébrique des couples agissant sur le système est nulle. Voyons maintenant le couple opposé par ces trois éléments individuellement.
Moment d'inertie
Dans le système mécanique de translation, la masse stocke l'énergie cinétique. De même, dans un système mécanique rotatif, le moment d'inertie stockekinetic energy.
Si un couple est appliqué sur un corps ayant un moment d'inertie J, puis il s'oppose à un couple opposé dû au moment d'inertie. Ce couple opposé est proportionnel à l'accélération angulaire du corps. Supposons que l'élasticité et le frottement soient négligeables.

$$T_j\propto\: \alpha$$
$$\Rightarrow T_j=J\alpha=J\frac{\text{d}^2\theta}{\text{d}t^2}$$
$$T=T_j=J\frac{\text{d}^2\theta}{\text{d}t^2}$$
Où,
T est le couple appliqué
Tj est le couple opposé dû au moment d'inertie
J est le moment d'inertie
α est l'accélération angulaire
θ est le déplacement angulaire
Ressort de torsion
Dans le système mécanique de translation, le ressort stocke l'énergie potentielle. De même, dans le système mécanique de rotation, les réserves de ressort de torsionpotential energy.
Si un couple est appliqué sur le ressort de torsion K, alors il s'oppose par un couple opposé dû à l'élasticité du ressort de torsion. Ce couple opposé est proportionnel au déplacement angulaire du ressort de torsion. Supposons que le moment d'inertie et de frottement soit négligeable.
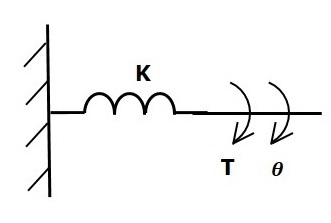
$$T_k\propto\: \theta$$
$$\Rightarrow T_k=K\theta$$
$$T=T_k=K\theta$$
Où,
T est le couple appliqué
Tk est le couple opposé dû à l'élasticité du ressort de torsion
K est la constante du ressort de torsion
θ est le déplacement angulaire
Dashpot
Si un couple est appliqué sur le dashpot B, puis il est opposé par un couple opposé dû au rotational frictiondu dashpot. Ce couple opposé est proportionnel à la vitesse angulaire du corps. Supposons que le moment d'inertie et d'élasticité soit négligeable.
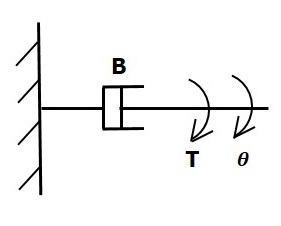
$$T_b\propto\: \omega$$
$$\Rightarrow T_b=B\omega=B\frac{\text{d}\theta}{\text{d}t}$$
$$T=T_b=B\frac{\text{d}\theta}{\text{d}t}$$
Où,
Tb est le couple opposé dû au frottement de rotation du dashpot
B est le coefficient de frottement rotationnel
ω est la vitesse angulaire
θ est le déplacement angulaire
On dit que deux systèmes sont analogous l'un à l'autre si les deux conditions suivantes sont remplies.
- Les deux systèmes sont physiquement différents
- La modélisation d'équations différentielles de ces deux systèmes est la même
Les systèmes électriques et les systèmes mécaniques sont deux systèmes physiquement différents. Il existe deux types d'analogies électriques des systèmes mécaniques de translation. Ce sont l'analogie de la tension de force et l'analogie du courant de force.
Analogie de tension de force
Dans l'analogie de la tension de force, les équations mathématiques de translational mechanical system sont comparées aux équations de maillage du système électrique.
Considérez le système mécanique de translation suivant, comme illustré dans la figure suivante.
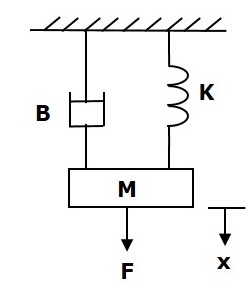
le force balanced equation car ce système est
$$F=F_m+F_b+F_k$$
$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (Equation 1)
Tenez compte du système électrique suivant, comme illustré dans la figure suivante. Ce circuit se compose d'une résistance, d'une inductance et d'un condensateur. Tous ces éléments électriques sont connectés en série. La tension d'entrée appliquée à ce circuit est$V$ volts et le courant circulant dans le circuit est $i$ Ampères.

L'équation de maillage pour ce circuit est
$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (Equation 2)
Remplacer, $i=\frac{\text{d}q}{\text{d}t}$ dans l'équation 2.
$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$
$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (Equation 3)
En comparant l'équation 1 et l'équation 3, nous obtiendrons les quantités analogues du système mécanique de translation et du système électrique. Le tableau suivant montre ces quantités analogues.
| Système mécanique translationnel | Système électrique |
|---|---|
| Force (F) | Tension (V) |
| Masse (M) | Inductance (L) |
| Coefficient de frottement (B) | Résistance (R) |
| Constante de ressort (K) | Réciproque de capacité $(\frac{1}{c})$ |
| Déplacement (x) | Charge (q) |
| Vitesse (v) | Actuel (i) |
De même, il existe une analogie de tension de couple pour les systèmes mécaniques rotatifs. Parlons maintenant de cette analogie.
Analogie de tension de couple
Dans cette analogie, les équations mathématiques de rotational mechanical system sont comparées aux équations de maillage du système électrique.
Le système mécanique de rotation est illustré dans la figure suivante.

L'équation de couple équilibré est
$$T=T_j+T_b+T_k$$
$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (Equation 4)
En comparant l'équation 4 et l'équation 3, nous obtiendrons les quantités analogues de système mécanique de rotation et de système électrique. Le tableau suivant montre ces quantités analogues.
| Système mécanique de rotation | Système électrique |
|---|---|
| Couple (T) | Tension (V) |
| Moment d'inertie (J) | Inductance (L) |
| Coefficient de friction rotationnel (B) | Résistance (R) |
| Constante du ressort de torsion (K) | Réciproque de capacité $(\frac{1}{c})$ |
| Déplacement angulaire (θ) | Charge (q) |
| Vitesse angulaire (ω) | Actuel (i) |
Analogie de courant de force
Dans l'analogie du courant de force, les équations mathématiques du translational mechanical system sont comparées aux équations nodales du système électrique.
Tenez compte du système électrique suivant, comme illustré dans la figure suivante. Ce circuit se compose d'une source de courant, d'une résistance, d'un inducteur et d'un condensateur. Tous ces éléments électriques sont connectés en parallèle.

L'équation nodale est
$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (Equation 5)
Remplacer, $V=\frac{\text{d}\Psi}{\text{d}t}$ dans l'équation 5.
$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$
$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (Equation 6)
En comparant l'équation 1 et l'équation 6, nous obtiendrons les quantités analogues du système mécanique de translation et du système électrique. Le tableau suivant montre ces quantités analogues.
| Système mécanique translationnel | Système électrique |
|---|---|
| Force (F) | Actuel (i) |
| Masse (M) | Capacité (C) |
| Coefficient de frottement (B) | Réciproque de résistance$(\frac{1}{R})$ |
| Constante de ressort (K) | Réciproque d'inductance$(\frac{1}{L})$ |
| Déplacement (x) | Flux magnétique (ψ) |
| Vitesse (v) | Tension (V) |
De même, il existe une analogie du courant de couple pour les systèmes mécaniques rotatifs. Parlons maintenant de cette analogie.
Analogie du courant de couple
Dans cette analogie, les équations mathématiques du rotational mechanical system sont comparées aux équations de maillage nodal du système électrique.
En comparant l'équation 4 et l'équation 6, nous obtiendrons les quantités analogues de système mécanique de rotation et de système électrique. Le tableau suivant montre ces quantités analogues.
| Système mécanique de rotation | Système électrique |
|---|---|
| Couple (T) | Actuel (i) |
| Moment d'inertie (J) | Capacité (C) |
| Coefficient de friction rotationnel (B) | Réciproque de résistance$(\frac{1}{R})$ |
| Constante du ressort de torsion (K) | Réciproque d'inductance$(\frac{1}{L})$ |
| Déplacement angulaire (θ) | Flux magnétique (ψ) |
| Vitesse angulaire (ω) | Tension (V) |
Dans ce chapitre, nous avons discuté des analogies électriques des systèmes mécaniques. Ces analogies sont utiles pour étudier et analyser le système non électrique comme le système mécanique à partir d'un système électrique analogue.
Les schémas de principe se composent d'un seul bloc ou d'une combinaison de blocs. Ceux-ci sont utilisés pour représenter les systèmes de contrôle sous forme picturale.
Éléments de base du diagramme
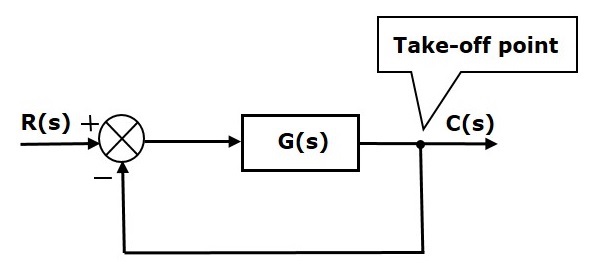
Les éléments de base d'un schéma fonctionnel sont un bloc, le point de sommation et le point de décollage. Considérons le schéma de principe d'un système de commande en boucle fermée comme illustré dans la figure suivante pour identifier ces éléments.

Le schéma de principe ci-dessus se compose de deux blocs ayant les fonctions de transfert G (s) et H (s). Il a également un point de sommation et un point de décollage. Les flèches indiquent la direction du flux des signaux. Parlons maintenant de ces éléments un par un.
Bloquer
La fonction de transfert d'un composant est représentée par un bloc. Le bloc a une seule entrée et une seule sortie.
La figure suivante montre un bloc ayant l'entrée X (s), la sortie Y (s) et la fonction de transfert G (s).

Fonction de transfert,$G(s)=\frac{Y(s)}{X(s)}$
$$\Rightarrow Y(s)=G(s)X(s)$$
La sortie du bloc est obtenue en multipliant la fonction de transfert du bloc par l'entrée.
Point de sommation
Le point de sommation est représenté par un cercle comportant une croix (X) à l'intérieur. Il a deux entrées ou plus et une seule sortie. Il produit la somme algébrique des entrées. Il effectue également la sommation ou la soustraction ou la combinaison de la sommation et de la soustraction des entrées en fonction de la polarité des entrées. Voyons ces trois opérations une par une.
La figure suivante montre le point de sommation avec deux entrées (A, B) et une sortie (Y). Ici, les entrées A et B ont un signe positif. Ainsi, le point de sommation produit la sortie, Y commesum of A and B.
c'est-à-dire, Y = A + B.

La figure suivante montre le point de sommation avec deux entrées (A, B) et une sortie (Y). Ici, les entrées A et B ont des signes opposés, c'est-à-dire que A a un signe positif et B a un signe négatif. Ainsi, le point de sommation produit la sortieY comme le difference of A and B.
Y = A + (-B) = A - B.

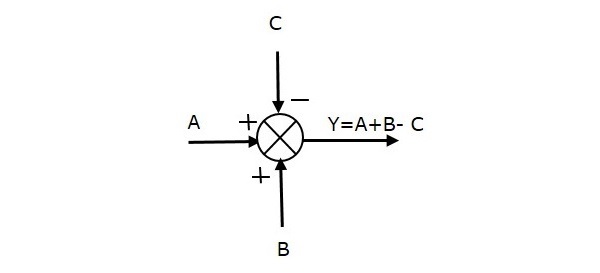
La figure suivante montre le point de sommation avec trois entrées (A, B, C) et une sortie (Y). Ici, les entrées A et B ont des signes positifs et C a un signe négatif. Ainsi, le point de sommation produit la sortieY comme
Y = A + B + (−C) = A + B - C.
Point de décollage
Le point de décollage est un point à partir duquel le même signal d'entrée peut passer par plusieurs branches. Cela signifie qu'avec l'aide du point de décollage, nous pouvons appliquer la même entrée à un ou plusieurs blocs, en additionnant les points.
Dans la figure suivante, le point de décollage est utilisé pour connecter la même entrée, R (s) à deux autres blocs.

Dans la figure suivante, le point de décollage est utilisé pour connecter la (les) sortie (s), comme l'une des entrées au point de sommation.
Représentation schématique des systèmes électriques
Dans cette section, représentons un système électrique avec un schéma de principe. Les systèmes électriques contiennent principalement trois éléments de base -resistor, inductor and capacitor.
Considérez une série de circuits RLC comme indiqué dans la figure suivante. Où, V i (t) et V o (t) sont les tensions d'entrée et de sortie. Soit i (t) le courant traversant le circuit. Ce circuit est dans le domaine temporel.

En appliquant la transformée de Laplace à ce circuit, obtiendra le circuit dans le domaine s. Le circuit est comme illustré dans la figure suivante.
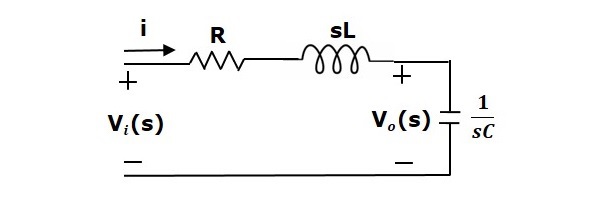
À partir du circuit ci-dessus, nous pouvons écrire
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (Equation 1)
$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (Equation 2)
Dessinons maintenant les schémas de principe de ces deux équations individuellement. Et puis combinez correctement ces schémas de principe afin d'obtenir le schéma de principe global de la série de circuits RLC (s-domaine).
L'équation 1 peut être implémentée avec un bloc ayant la fonction de transfert, $\frac{1}{R+sL}$. L'entrée et la sortie de ce bloc sont$\left \{ V_i(s)-V_o(s) \right \}$ et $I(s)$. Nous avons besoin d'un point de sommation pour obtenir$\left \{ V_i(s)-V_o(s) \right \}$. Le schéma de principe de l'équation 1 est illustré dans la figure suivante.

L'équation 2 peut être implémentée avec un bloc ayant une fonction de transfert, $\frac{1}{sC}$. L'entrée et la sortie de ce bloc sont$I(s)$ et $V_o(s)$. Le schéma de principe de l'équation 2 est illustré dans la figure suivante.

Le schéma de principe global de la série de circuits RLC (s-domaine) est illustré dans la figure suivante.

De même, vous pouvez dessiner le block diagram de tout circuit ou système électrique en suivant simplement cette procédure simple.
Convertissez le circuit électrique du domaine temporel en un circuit électrique du domaine s en appliquant la transformée de Laplace.
Notez les équations pour le courant traversant tous les éléments de branche en série et la tension sur toutes les branches de shunt.
Dessinez les diagrammes de toutes les équations ci-dessus individuellement.
Combinez correctement tous ces schémas de principe afin d'obtenir le schéma de principe global du circuit électrique (domaine s).
L'algèbre du diagramme n'est rien d'autre que l'algèbre impliquée dans les éléments de base du diagramme. Cette algèbre traite de la représentation picturale des équations algébriques.
Connexions de base pour les blocs
Il existe trois types de base de connexions entre deux blocs.
Connexion en série
La connexion en série est également appelée cascade connection. Dans la figure suivante, deux blocs ayant des fonctions de transfert$G_1(s)$ et $G_2(s)$ sont connectés en série.

Pour cette combinaison, nous obtiendrons la sortie $Y(s)$ comme
$$Y(s)=G_2(s)Z(s)$$
Où, $Z(s)=G_1(s)X(s)$
$$\Rightarrow Y(s)=G_2(s)[G_1(s)X(s)]=G_1(s)G_2(s)X(s)$$
$$\Rightarrow Y(s)=\lbrace G_1(s)G_2(s)\rbrace X(s)$$
Comparez cette équation avec la forme standard de l'équation de sortie, $Y(s)=G(s)X(s)$. Où,$G(s) = G_1(s)G_2(s)$.
Cela signifie que nous pouvons représenter le series connectionde deux blocs avec un seul bloc. La fonction de transfert de ce bloc unique est laproduct of the transfer functionsde ces deux blocs. Le schéma fonctionnel équivalent est présenté ci-dessous.
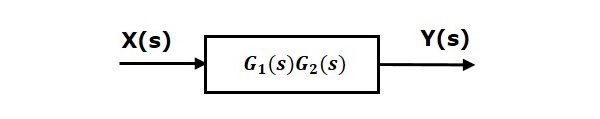
De même, vous pouvez représenter une connexion en série de «n» blocs avec un seul bloc. La fonction de transfert de ce bloc unique est le produit des fonctions de transfert de tous ces «n» blocs.
Connexion parallèle
Les blocs qui sont connectés dans parallel aura le same input. Dans la figure suivante, deux blocs ayant des fonctions de transfert$G_1(s)$ et $G_2(s)$sont connectés en parallèle. Les sorties de ces deux blocs sont connectées au point de sommation.

Pour cette combinaison, nous obtiendrons la sortie $Y(s)$ comme
$$Y(s)=Y_1(s)+Y_2(s)$$
Où, $Y_1(s)=G_1(s)X(s)$ et $Y_2(s)=G_2(s)X(s)$
$$\Rightarrow Y(s)=G_1(s)X(s)+G_2(s)X(s)=\lbrace G_1(s)+G_2(s)\rbrace X(s)$$
Comparez cette équation avec la forme standard de l'équation de sortie, $Y(s)=G(s)X(s)$.
Où, $G(s)=G_1(s)+G_2(s)$.
Cela signifie que nous pouvons représenter le parallel connectionde deux blocs avec un seul bloc. La fonction de transfert de ce bloc unique est lasum of the transfer functionsde ces deux blocs. Le schéma fonctionnel équivalent est présenté ci-dessous.

De même, vous pouvez représenter une connexion parallèle de «n» blocs avec un seul bloc. La fonction de transfert de ce bloc unique est la somme algébrique des fonctions de transfert de tous ces «n» blocs.
Connexion de rétroaction
Comme nous l'avons vu dans les chapitres précédents, il existe deux types de feedback- rétroaction positive et rétroaction négative. La figure suivante montre le système de contrôle de rétroaction négative. Ici, deux blocs ayant des fonctions de transfert$G(s)$ et $H(s)$ forment une boucle fermée.

La sortie du point de sommation est -
$$E(s)=X(s)-H(s)Y(s)$$
Le résultat $Y(s)$ est -
$$Y(s)=E(s)G(s)$$
Remplacer $E(s)$ valeur dans l'équation ci-dessus.
$$Y(s)=\left \{ X(s)-H(s)Y(s)\rbrace G(s) \right\}$$
$$Y(s)\left \{ 1+G(s)H(s)\rbrace = X(s)G(s) \right\}$$
$$\Rightarrow \frac{Y(s)}{X(s)}=\frac{G(s)}{1+G(s)H(s)}$$
Par conséquent, la fonction de transfert en boucle fermée à rétroaction négative est $\frac{G(s)}{1+G(s)H(s)}$
Cela signifie que nous pouvons représenter la connexion de rétroaction négative de deux blocs avec un seul bloc. La fonction de transfert de ce bloc unique est la fonction de transfert en boucle fermée de la rétroaction négative. Le schéma fonctionnel équivalent est présenté ci-dessous.

De même, vous pouvez représenter la connexion de rétroaction positive de deux blocs avec un seul bloc. La fonction de transfert de ce bloc unique est la fonction de transfert en boucle fermée de la rétroaction positive, c'est-à-dire,$\frac{G(s)}{1-G(s)H(s)}$
Algèbre de diagramme de blocs pour la somme des points
Il existe deux possibilités de décaler les points de sommation par rapport aux blocs -
- Décalage du point de sommation après le bloc
- Décalage du point de sommation avant le bloc
Voyons maintenant quel genre d'arrangements il faut faire dans les deux cas ci-dessus, un par un.
Décalage du point de sommation après le bloc
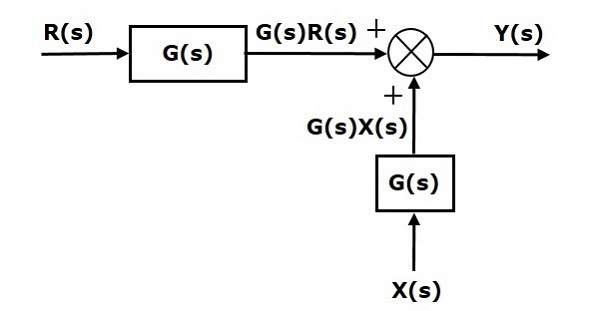
Considérez le schéma de principe illustré dans la figure suivante. Ici, le point de sommation est présent avant le bloc.

Le point de sommation a deux entrées $R(s)$ et $X(s)$. La sortie de celui-ci est$\left \{R(s)+X(s)\right\}$.
Donc, l'entrée du bloc $G(s)$ est $\left \{R(s)+X(s)\right \}$ et le résultat est -
$$Y(s)=G(s)\left \{R(s)+X(s)\right \}$$
$\Rightarrow Y(s)=G(s)R(s)+G(s)X(s)$ (Equation 1)
Maintenant, décalez le point de sommation après le bloc. Ce schéma de principe est illustré dans la figure suivante.

Sortie du bloc $G(s)$ est $G(s)R(s)$.
La sortie du point de sommation est
$Y(s)=G(s)R(s)+X(s)$ (Equation 2)
Comparez l'équation 1 et l'équation 2.
Le premier terme $‘G(s) R(s)’$est la même dans les deux équations. Mais, il y a une différence dans le deuxième mandat. Afin d'obtenir le deuxième terme également, nous avons besoin d'un bloc supplémentaire$G(s)$. C'est avoir l'entrée$X(s)$ et la sortie de ce bloc est donnée comme entrée au point de sommation au lieu de $X(s)$. Ce schéma de principe est illustré dans la figure suivante.
Décalage du point de sommation avant le bloc
Considérez le schéma de principe illustré dans la figure suivante. Ici, le point de sommation est présent après le bloc.

La sortie de ce schéma fonctionnel est -
$Y(s)=G(s)R(s)+X(s)$ (Equation 3)
Maintenant, déplacez le point de sommation avant le bloc. Ce schéma de principe est illustré dans la figure suivante.

La sortie de ce schéma fonctionnel est -
$Y(S)=G(s)R(s)+G(s)X(s)$ (Equation 4)
Comparez l'équation 3 et l'équation 4,
Le premier terme $‘G(s) R(s)’$est la même dans les deux équations. Mais, il y a une différence dans le deuxième mandat. Afin d'obtenir le deuxième terme également, nous avons besoin d'un bloc supplémentaire$\frac{1}{G(s)}$. C'est avoir l'entrée$X(s)$ et la sortie de ce bloc est donnée comme entrée au point de sommation au lieu de $X(s)$. Ce schéma de principe est illustré dans la figure suivante.

Algèbre de schéma fonctionnel pour les points de décollage
Il existe deux possibilités de décaler les points de décollage par rapport aux blocs -
- Changement du point de décollage après le blocage
- Décalage du point de décollage avant le blocage
Voyons maintenant quel genre d'arrangements il faut faire dans les deux cas ci-dessus, un par un.
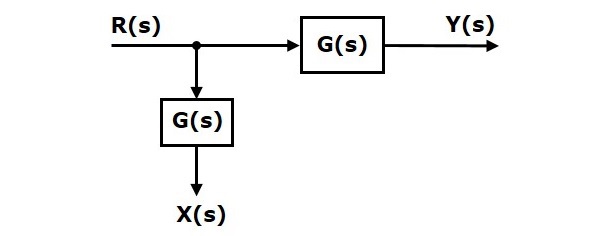
Changement du point de décollage après le blocage
Considérez le schéma de principe illustré dans la figure suivante. Dans ce cas, le point de décollage est présent avant le blocage.

Ici, $X(s)=R(s)$ et $Y(s)=G(s)R(s)$
Lorsque vous déplacez le point de décollage après le blocage, la sortie $Y(s)$sera le même. Mais, il y a une différence dans$X(s)$valeur. Donc, pour obtenir la même chose$X(s)$ valeur, nous avons besoin d'un bloc de plus $\frac{1}{G(s)}$. C'est avoir l'entrée$Y(s)$ et la sortie est $X(s)$. Ce schéma de principe est illustré dans la figure suivante.

Changement du point de décollage avant le blocage
Considérez le schéma de principe illustré dans la figure suivante. Ici, le point de décollage est présent après le blocage.

Ici, $X(s)=Y(s)=G(s)R(s)$
Lorsque vous déplacez le point de décollage avant le bloc, la sortie $Y(s)$sera le même. Mais, il y a une différence dans$X(s)$valeur. Donc, pour obtenir la même chose$X(s)$ valeur, nous avons besoin d'un bloc de plus $G(s)$. C'est avoir l'entrée$R(s)$ et la sortie est $X(s)$. Ce schéma de principe est illustré dans la figure suivante.
Les concepts abordés dans le chapitre précédent sont utiles pour réduire (simplifier) les schémas fonctionnels.
Règles de réduction des schémas fonctionnels
Suivez ces règles pour simplifier (réduire) le diagramme, qui comporte de nombreux blocs, points de sommation et points de décollage.
Rule 1 - Vérifier les blocs connectés en série et simplifier.
Rule 2 - Vérifier les blocs connectés en parallèle et simplifier.
Rule 3 - Vérifier les blocs connectés en boucle de rétroaction et simplifier.
Rule 4 - En cas de difficulté avec le point de décollage lors de la simplification, déplacez-le vers la droite.
Rule 5 - S'il y a des difficultés avec le point de sommation lors de la simplification, déplacez-le vers la gauche.
Rule 6 - Répétez les étapes ci-dessus jusqu'à ce que vous obteniez le formulaire simplifié, c'est-à-dire un seul bloc.
Note - La fonction de transfert présente dans ce bloc unique est la fonction de transfert du schéma de principe global.
Example
Consider the block diagram shown in the following figure. Let us simplify (reduce) this block diagram using the block diagram reduction rules.

Step 1 − Use Rule 1 for blocks $G_1$ and $G_2$. Use Rule 2 for blocks $G_3$ and $G_4$. The modified block diagram is shown in the following figure.

Step 2 − Use Rule 3 for blocks $G_1G_2$ and $H_1$. Use Rule 4 for shifting take-off point after the block $G_5$. The modified block diagram is shown in the following figure.

Step 3 − Use Rule 1 for blocks $(G_3 + G_4)$ and $G_5$. The modified block diagram is shown in the following figure.

Step 4 − Use Rule 3 for blocks $(G_3 + G_4)G_5$ and $H_3$. The modified block diagram is shown in the following figure.

Step 5 − Use Rule 1 for blocks connected in series. The modified block diagram is shown in the following figure.

Step 6 − Use Rule 3 for blocks connected in feedback loop. The modified block diagram is shown in the following figure. This is the simplified block diagram.
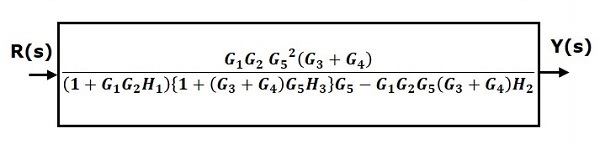
Therefore, the transfer function of the system is
$$\frac{Y(s)}{R(s)}=\frac{G_1G_2G_5^2(G_3+G_4)}{(1+G_1G_2H_1)\lbrace 1+(G_3+G_4)G_5H_3\rbrace G_5-G_1G_2G_5(G_3+G_4)H_2}$$
Note − Follow these steps in order to calculate the transfer function of the block diagram having multiple inputs.
Step 1 − Find the transfer function of block diagram by considering one input at a time and make the remaining inputs as zero.
Step 2 − Repeat step 1 for remaining inputs.
Step 3 − Get the overall transfer function by adding all those transfer functions.
The block diagram reduction process takes more time for complicated systems. Because, we have to draw the (partially simplified) block diagram after each step. So, to overcome this drawback, use signal flow graphs (representation).
In the next two chapters, we will discuss about the concepts related to signal flow graphs, i.e., how to represent signal flow graph from a given block diagram and calculation of transfer function just by using a gain formula without doing any reduction process.
Signal flow graph is a graphical representation of algebraic equations. In this chapter, let us discuss the basic concepts related signal flow graph and also learn how to draw signal flow graphs.
Basic Elements of Signal Flow Graph
Nodes and branches are the basic elements of signal flow graph.
Node
Node is a point which represents either a variable or a signal. There are three types of nodes — input node, output node and mixed node.
Input Node − It is a node, which has only outgoing branches.
Output Node − It is a node, which has only incoming branches.
Mixed Node − It is a node, which has both incoming and outgoing branches.
Example
Let us consider the following signal flow graph to identify these nodes.

The nodes present in this signal flow graph are y1, y2, y3 and y4.
y1 and y4 are the input node and output node respectively.
y2 and y3 are mixed nodes.
Branch
Branch is a line segment which joins two nodes. It has both gain and direction. For example, there are four branches in the above signal flow graph. These branches have gains of a, b, c and -d.
Construction of Signal Flow Graph
Let us construct a signal flow graph by considering the following algebraic equations −
$$y_2=a_{12}y_1+a_{42}y_4$$
$$y_3=a_{23}y_2+a_{53}y_5$$
$$y_4=a_{34}y_3$$
$$y_5=a_{45}y_4+a_{35}y_3$$
$$y_6=a_{56}y_5$$
There will be six nodes (y1, y2, y3, y4, y5 and y6) and eight branches in this signal flow graph. The gains of the branches are a12, a23, a34, a45, a56, a42, a53 and a35.
To get the overall signal flow graph, draw the signal flow graph for each equation, then combine all these signal flow graphs and then follow the steps given below −
Step 1 − Signal flow graph for $y_2 = a_{13}y_1 + a_{42}y_4$ is shown in the following figure.

Step 2 − Signal flow graph for $y_3 = a_{23}y_2 + a_{53}y_5$ is shown in the following figure.

Step 3 − Signal flow graph for $y_4 = a_{34}y_3$ is shown in the following figure.

Step 4 − Signal flow graph for $y_5 = a_{45}y_4 + a_{35}y_3$ is shown in the following figure.

Step 5 − Signal flow graph for $y_6 = a_{56}y_5$ is shown in the following figure.

Step 6 − Signal flow graph of overall system is shown in the following figure.

Conversion of Block Diagrams into Signal Flow Graphs
Follow these steps for converting a block diagram into its equivalent signal flow graph.
Represent all the signals, variables, summing points and take-off points of block diagram as nodes in signal flow graph.
Represent the blocks of block diagram as branches in signal flow graph.
Represent the transfer functions inside the blocks of block diagram as gains of the branches in signal flow graph.
Connect the nodes as per the block diagram. If there is connection between two nodes (but there is no block in between), then represent the gain of the branch as one. For example, between summing points, between summing point and takeoff point, between input and summing point, between take-off point and output.
Exemple
Convertissons le schéma fonctionnel suivant en son graphique de flux de signaux équivalent.

Représente le signal d'entrée $R(s)$ et signal de sortie $C(s)$ du diagramme en tant que nœud d'entrée $R(s)$ et noeud de sortie $C(s)$ du graphique de flux de signal.
Juste pour référence, les nœuds restants (y 1 à y 9 ) sont étiquetés dans le diagramme. Il existe neuf nœuds autres que les nœuds d'entrée et de sortie. Soit quatre nœuds pour quatre points de sommation, quatre nœuds pour quatre points de décollage et un nœud pour la variable entre les blocs$G_1$ et $G_2$.
La figure suivante montre le graphique de flux de signal équivalent.

À l'aide de la formule de gain de Mason (discutée dans le chapitre suivant), vous pouvez calculer la fonction de transfert de ce graphique de flux de signal. C'est l'avantage des graphiques de flux de signaux. Ici, il n'est pas nécessaire de simplifier (réduire) les graphiques de flux de signaux pour le calcul de la fonction de transfert.
Parlons maintenant de la formule de gain de Mason. Supposons qu'il y ait «N» trajets aller dans un graphe de flux de signaux. Le gain entre les nœuds d'entrée et de sortie d'un graphe de flux de signaux n'est rien d'autre que letransfer functiondu système. Il peut être calculé en utilisant la formule de gain de Mason.
Mason’s gain formula is
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^N _{i=1}P_i\Delta _i}{\Delta}$$
Où,
C(s) est le nœud de sortie
R(s) est le nœud d'entrée
T est la fonction de transfert ou le gain entre $R(s)$ et $C(s)$
Piest le i ème gain du trajet aller
$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$
$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$
$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$
Δ i est obtenu à partir de Δ en supprimant les boucles qui touchent le i ème trajet aller .
Considérez le graphique de flux de signaux suivant afin de comprendre la terminologie de base impliquée ici.

Chemin
C'est un parcours de branches d'un nœud à n'importe quel autre nœud dans le sens des flèches de branche. Il ne doit traverser aucun nœud plus d'une fois.
Examples - $y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5$ et $y_5 \rightarrow y_3 \rightarrow y_2$
Chemin avant
Le chemin qui existe entre le nœud d'entrée et le nœud de sortie est appelé forward path.
Examples - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ et $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
Gain du chemin avant
Il est obtenu en calculant le produit de tous les gains de branche du chemin aller.
Examples - $abcde$ est le gain sur la voie aller de $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ et abge est le gain sur la voie aller de $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
Boucle
Le chemin qui commence à partir d'un nœud et se termine au même nœud est appelé loop. C'est donc un chemin fermé.
Examples - $y_2 \rightarrow y_3 \rightarrow y_2$ et $y_3 \rightarrow y_5 \rightarrow y_3$.
Gain de boucle
Il est obtenu en calculant le produit de tous les gains de branche d'une boucle.
Examples - $b_j$ est le gain de boucle de $y_2 \rightarrow y_3 \rightarrow y_2$ et $g_h$ est le gain de boucle de $y_3 \rightarrow y_5 \rightarrow y_3$.
Boucles sans contact
Ce sont les boucles, qui ne devraient avoir aucun nœud commun.
Examples - Les boucles, $y_2 \rightarrow y_3 \rightarrow y_2$ et $y_4 \rightarrow y_5 \rightarrow y_4$ sont sans contact.
Calcul de la fonction de transfert à l'aide de la formule de gain de Mason
Considérons le même graphe de flux de signal pour trouver la fonction de transfert.

Nombre de trajets aller, N = 2.
La première voie à suivre est - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$.
Premier gain de voie avant, $p_1 = abcde$.
La deuxième voie à suivre est - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
Deuxième gain de voie avant, $p_2 = abge$.
Nombre de boucles individuelles, L = 5.
Les boucles sont - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_3 \rightarrow y_5 \rightarrow y_3$, $y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_3$, $y_4 \rightarrow y_5 \rightarrow y_4$ et $y_5 \rightarrow y_5$.
Les gains de boucle sont - $l_1 = bj$, $l_2 = gh$, $l_3 = cdh$, $l_4 = di$ et $l_5 = f$.
Nombre de deux boucles sans contact = 2.
La première paire de boucles sans contact est - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_4 \rightarrow y_5 \rightarrow y_4$.
Gagnez le produit de la première paire de boucles sans contact, $l_1l_4 = bjdi$
La deuxième paire de boucles sans contact est - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_5 \rightarrow y_5$.
Le produit de gain de la deuxième paire de boucles non touchantes est - $l_1l_5 = bjf$
Un nombre plus élevé de (plus de deux) boucles sans contact n'est pas présent dans ce graphique de flux de signaux.
Nous savons,
$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$
$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$
$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$
Remplacez les valeurs de l'équation ci-dessus,
$\Delta =1-(bj+gh+cdh+di+f)+(bjdi+bjf)-(0)$
$\Rightarrow \Delta=1-(bj+gh+cdh+di+f)+bjdi+bjf$
Il n'y a pas de boucle qui ne touche pas le premier chemin aller.
Alors, $\Delta_1=1$.
De même, $\Delta_2=1$. Depuis, pas de boucle qui ne touche pas le deuxième chemin aller.
Substitut, N = 2 dans la formule de gain de Mason
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^2 _{i=1}P_i\Delta _i}{\Delta}$$
$$T=\frac{C(s)}{R(s)}=\frac{P_1\Delta_1+P_2\Delta_2}{\Delta}$$
Remplacez toutes les valeurs nécessaires dans l'équation ci-dessus.
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)1+(abge)1}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
$$\Rightarrow T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
Par conséquent, la fonction de transfert est -
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
Nous pouvons analyser la réponse des systèmes de contrôle à la fois dans le domaine temporel et dans le domaine fréquentiel. Nous discuterons de l'analyse de la réponse en fréquence des systèmes de contrôle dans les chapitres suivants. Parlons maintenant de l'analyse de la réponse temporelle des systèmes de contrôle.
Qu'est-ce que la réponse temporelle?
Si la sortie du système de contrôle pour une entrée varie en fonction du temps, alors on l'appelle le time responsedu système de contrôle. La réponse temporelle se compose de deux parties.
- Réponse transitoire
- Réponse en régime permanent
La réponse du système de commande dans le domaine temporel est illustrée dans la figure suivante.

Ici, les états transitoire et stable sont indiqués sur la figure. Les réponses correspondant à ces états sont appelées réponses transitoires et stables.
Mathématiquement, nous pouvons écrire la réponse temporelle c (t) comme
$$c(t)=c_{tr}(t)+c_{ss}(t)$$
Où,
- c tr (t) est la réponse transitoire
- c ss (t) est la réponse en régime permanent
Réponse transitoire
Après avoir appliqué l'entrée au système de contrôle, la sortie prend un certain temps pour atteindre un état stable. Ainsi, la sortie sera dans un état transitoire jusqu'à ce qu'elle passe à un état stable. Par conséquent, la réponse du système de contrôle pendant l'état transitoire est appeléetransient response.
La réponse transitoire sera nulle pour les grandes valeurs de «t». Idéalement, cette valeur de «t» est l'infini et pratiquement, elle est cinq fois constante.
Mathématiquement, nous pouvons l'écrire comme
$$\lim_{t\rightarrow \infty }c_{tr}(t)=0$$
Réponse en régime permanent
La partie de la réponse temporelle qui reste même après que la réponse transitoire a une valeur nulle pour les grandes valeurs de `` t '' est appelée steady state response. Cela signifie que la réponse transitoire sera nulle même en régime permanent.
Example
Trouvons les termes transitoire et stationnaire de la réponse temporelle du système de contrôle $c(t)=10+5e^{-t}$
Ici, le deuxième terme $5e^{-t}$ sera zéro car tdésigne l'infini. Donc, c'est letransient term. Et le premier terme 10 reste le mêmets'approche de l'infini. Donc, c'est lesteady state term.
Signaux de test standard
Les signaux de test standard sont impulsion, pas, rampe et parabolique. Ces signaux sont utilisés pour connaître les performances des systèmes de contrôle en utilisant la réponse temporelle de la sortie.
Signal d'impulsion de l'unité
Un signal d'impulsion unitaire, δ (t) est défini comme
$\delta (t)=0$ pour $t\neq 0$
et $\int_{0^-}^{0^+} \delta (t)dt=1$
La figure suivante montre le signal d'impulsion de l'unité.

Ainsi, le signal d'impulsion unitaire n'existe que lorsque «t» est égal à zéro. La zone de ce signal sous un petit intervalle de temps autour de «t» est égale à zéro est un. La valeur du signal d'impulsion unitaire est zéro pour toutes les autres valeurs de «t».
Signal d'étape de l'unité
Un signal de pas unitaire, u (t) est défini comme
$$u(t)=1;t\geq 0$$
$=0; t<0$
La figure suivante montre le signal de pas d'unité.

Ainsi, le signal de pas unitaire existe pour toutes les valeurs positives de «t», y compris zéro. Et sa valeur est de un pendant cet intervalle. La valeur du signal de pas unitaire est zéro pour toutes les valeurs négatives de «t».
Signal de rampe de l'unité
Un signal de rampe unitaire, r (t) est défini comme
$$r(t)=t; t\geq 0$$
$=0; t<0$
Nous pouvons écrire le signal de rampe d'unité, $r(t)$ en termes de signal de pas unitaire, $u(t)$ comme
$$r(t)=tu(t)$$
La figure suivante montre le signal de rampe de l'unité.

Ainsi, le signal de rampe d'unité existe pour toutes les valeurs positives de «t», y compris zéro. Et sa valeur augmente linéairement par rapport à «t» pendant cet intervalle. La valeur du signal de rampe unitaire est zéro pour toutes les valeurs négatives de «t».
Signal parabolique d'unité
Un signal parabolique unitaire, p (t) est défini comme,
$$p(t)=\frac{t^2}{2}; t\geq 0$$
$=0; t<0$
Nous pouvons écrire un signal parabolique unitaire, $p(t)$ en termes de signal de pas unitaire, $u(t)$ comme,
$$p(t)=\frac{t^2}{2}u(t)$$
La figure suivante montre le signal parabolique de l'unité.
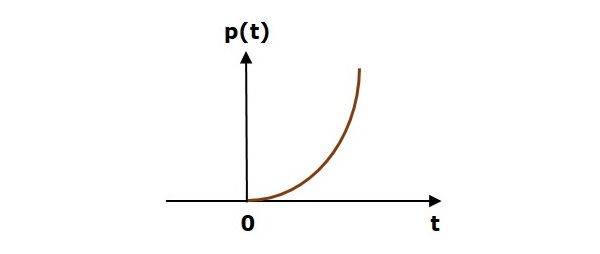
Ainsi, le signal parabolique unitaire existe pour toutes les valeurs positives de ‘t’y compris zéro. Et sa valeur augmente de manière non linéaire par rapport à «t» pendant cet intervalle. La valeur du signal parabolique unitaire est zéro pour toutes les valeurs négatives de «t».
Dans ce chapitre, parlons de la réponse temporelle du système de premier ordre. Considérez le schéma de principe suivant du système de contrôle en boucle fermée. Ici, une fonction de transfert en boucle ouverte,$\frac{1}{sT}$ est lié à une rétroaction négative unitaire.

Nous savons que la fonction de transfert du système de contrôle en boucle fermée a une rétroaction négative unitaire comme,
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
Remplacer, $G(s)=\frac{1}{sT}$ dans l'équation ci-dessus.
$$\frac{C(s)}{R(s)}=\frac{\frac{1}{sT}}{1+\frac{1}{sT}}=\frac{1}{sT+1}$$
La puissance de s est une dans le terme dénominateur. Par conséquent, la fonction de transfert ci-dessus est du premier ordre et le système est ditfirst order system.
Nous pouvons réécrire l'équation ci-dessus comme
$$C(s)=\left ( \frac{1}{sT+1} \right )R(s)$$
Où,
C(s) est la transformée de Laplace du signal de sortie c (t),
R(s) est la transformée de Laplace du signal d'entrée r (t), et
T est la constante de temps.
Suivez ces étapes pour obtenir la réponse (sortie) du système de premier ordre dans le domaine temporel.
Prendre la transformée de Laplace du signal d'entrée $r(t)$.
Considérez l'équation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Remplacer $R(s)$ valeur dans l'équation ci-dessus.
Faire des fractions partielles de $C(s)$ si nécessaire.
Appliquer la transformation de Laplace inverse à $C(s)$.
Dans le chapitre précédent, nous avons vu les signaux de test standard tels que l'impulsion, le pas, la rampe et la parabolique. Découvrons maintenant les réponses du premier système d'ordre pour chaque entrée, une par une. Le nom de la réponse est donné en fonction du nom du signal d'entrée. Par exemple, la réponse du système pour une entrée impulsionnelle est appelée réponse impulsionnelle.
Réponse impulsionnelle du système de premier ordre
Prendre en compte unit impulse signal comme entrée du système de premier ordre.
Alors, $r(t)=\delta (t)$
Appliquez la transformation de Laplace des deux côtés.
$R(s)=1$
Considérez l'équation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Remplacer, $R(s) = 1$ dans l'équation ci-dessus.
$$C(s)=\left ( \frac{1}{sT+1} \right )(1)=\frac{1}{sT+1}$$
Réorganisez l'équation ci-dessus dans l'une des formes standard de transformées de Laplace.
$$C(s)=\frac{1}{T\left (\ s+\frac{1}{T} \right )} \Rightarrow C(s)=\frac{1}{T}\left ( \frac{1}{s+\frac{1}{T}} \right )$$
Appliquez la transformée de Laplace inverse des deux côtés.
$$c(t)=\frac{1}{T}e^\left ( {-\frac{t}{T}} \right )u(t)$$
La réponse impulsionnelle de l'unité est illustrée dans la figure suivante.
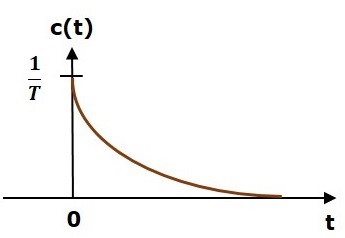
le unit impulse response, c (t) est un signal décroissant exponentiel pour les valeurs positives de «t» et il est nul pour les valeurs négatives de «t».
Réponse échelonnée du système de premier ordre
Prendre en compte unit step signal comme entrée du système de premier ordre.
Alors, $r(t)=u(t)$
Appliquez la transformation de Laplace des deux côtés.
$$R(s)=\frac{1}{s}$$
Considérez l'équation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Remplacer, $R(s)=\frac{1}{s}$ dans l'équation ci-dessus.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s} \right )=\frac{1}{s\left ( sT+1 \right )}$$
Faites des fractions partielles de C (s).
$$C(s)=\frac{1}{s\left ( sT+1 \right )}=\frac{A}{s}+\frac{B}{sT+1}$$
$$\Rightarrow \frac{1}{s\left ( sT+1 \right )}=\frac{A\left ( sT+1 \right )+Bs}{s\left ( sT+1 \right )}$$
Des deux côtés, le terme dénominateur est le même. Donc, ils seront annulés l'un par l'autre. Par conséquent, assimilez les termes du numérateur.
$$1=A\left ( sT+1 \right )+Bs$$
En assimilant les termes constants des deux côtés, vous obtiendrez A = 1.
Remplacez A = 1 et assimilez le coefficient du s termes des deux côtés.
$$0=T+B \Rightarrow B=-T$$
Substitut, A = 1 et B = −T dans l'expansion de fraction partielle de $C(s)$.
$$C(s)=\frac{1}{s}-\frac{T}{sT+1}=\frac{1}{s}-\frac{T}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$
Appliquez la transformée de Laplace inverse des deux côtés.
$$c(t)=\left ( 1-e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
le unit step response, c (t) a à la fois les termes transitoire et stationnaire.
Le terme transitoire dans la réponse de pas unitaire est -
$$c_{tr}(t)=-e^{-\left ( \frac{t}{T} \right )}u(t)$$
Le terme en régime permanent dans la réponse en échelon unitaire est -
$$c_{ss}(t)=u(t)$$
La figure suivante montre la réponse de pas unitaire.

La valeur du unit step response, c(t)est nul à t = 0 et pour toutes les valeurs négatives de t. Il augmente progressivement à partir de la valeur zéro et atteint finalement un en régime permanent. Ainsi, la valeur de l'état stationnaire dépend de l'amplitude de l'entrée.
Réponse de rampe du système de premier ordre
Prendre en compte unit ramp signal comme entrée du système de premier ordre.
$So, r(t)=tu(t)$
Appliquez la transformation de Laplace des deux côtés.
$$R(s)=\frac{1}{s^2}$$
Considérez l'équation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Remplacer, $R(s)=\frac{1}{s^2}$ dans l'équation ci-dessus.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s^2} \right )=\frac{1}{s^2(sT+1)}$$
Faire des fractions partielles de $C(s)$.
$$C(s)=\frac{1}{s^2(sT+1)}=\frac{A}{s^2}+\frac{B}{s}+\frac{C}{sT+1}$$
$$\Rightarrow \frac{1}{s^2(sT+1)}=\frac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1)}$$
Des deux côtés, le terme dénominateur est le même. Donc, ils seront annulés l'un par l'autre. Par conséquent, assimilez les termes du numérateur.
$$1=A(sT+1)+Bs(sT+1)+Cs^2$$
En assimilant les termes constants des deux côtés, vous obtiendrez A = 1.
Remplacez, A = 1 et assimilez le coefficient des termes s des deux côtés.
$$0=T+B \Rightarrow B=-T$$
De même, remplacez B = −T et assimilez le coefficient de $s^2$termes des deux côtés. Tu auras$C=T^2$.
Remplacez A = 1, B = −T et $C = T^2$ dans l'expansion de fraction partielle de $C(s)$.
$$C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{sT+1}=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$
Appliquez la transformée de Laplace inverse des deux côtés.
$$c(t)=\left ( t-T+Te^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
le unit ramp response, c (t) a à la fois les termes transitoire et stationnaire.
Le terme transitoire dans la réponse de la rampe de l'unité est -
$$c_{tr}(t)=Te^{-\left ( \frac{t}{T} \right )}u(t)$$
Le terme en régime permanent dans la réponse de rampe de l'unité est -
$$c_{ss}(t)=(t-T)u(t)$$
La figure suivante montre la réponse de la rampe de l'unité.

le unit ramp response, c (t) suit le signal d'entrée de la rampe unitaire pour toutes les valeurs positives de t. Mais, il y a un écart de T unités par rapport au signal d'entrée.
Réponse parabolique du système du premier ordre
Prendre en compte unit parabolic signal comme entrée du système de premier ordre.
Alors, $r(t)=\frac{t^2}{2}u(t)$
Appliquez la transformation de Laplace des deux côtés.
$$R(s)=\frac{1}{s^3}$$
Considérez l'équation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Remplacer $R(s)=\frac{1}{s^3}$ dans l'équation ci-dessus.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left( \frac{1}{s^3} \right )=\frac{1}{s^3(sT+1)}$$
Faire des fractions partielles de $C(s)$.
$$C(s)=\frac{1}{s^3(sT+1)}=\frac{A}{s^3}+\frac{B}{s^2}+\frac{C}{s}+\frac{D}{sT+1}$$
Après avoir simplifié, vous obtiendrez les valeurs de A, B, C et D comme 1, $-T, \: T^2\: and \: −T^3$respectivement. Remplacez ces valeurs dans l'expansion de fraction partielle ci-dessus de C (s).
$C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^3}{sT+1} \: \Rightarrow C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^2}{s+\frac{1}{T}}$
Appliquez la transformée de Laplace inverse des deux côtés.
$$c(t)=\left ( \frac{t^2}{2} -Tt+T^2-T^2e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
le unit parabolic response, c (t) a à la fois les termes transitoire et stationnaire.
Le terme transitoire de la réponse parabolique unitaire est
$$C_{tr}(t)=-T^2e^{-\left ( \frac{t}{T} \right )}u(t)$$
Le terme à l'état d'équilibre dans la réponse parabolique unitaire est
$$C_{ss}(t)=\left ( \frac{t^2}{2} -Tt+T^2 \right )u(t)$$
A partir de ces réponses, nous pouvons conclure que les systèmes de contrôle du premier ordre ne sont pas stables avec la rampe et les entrées paraboliques car ces réponses continuent d'augmenter même à une durée infinie. Les systèmes de contrôle du premier ordre sont stables avec des entrées d'impulsion et de pas parce que ces réponses ont une sortie bornée. Mais, la réponse impulsionnelle n'a pas de terme d'état stable. Ainsi, le signal de pas est largement utilisé dans le domaine temporel pour analyser les systèmes de contrôle à partir de leurs réponses.
Dans ce chapitre, discutons de la réponse temporelle du système du second ordre. Considérez le schéma fonctionnel suivant du système de contrôle en boucle fermée. Ici, une fonction de transfert en boucle ouverte,$\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ est lié à une rétroaction négative unitaire.

Nous savons que la fonction de transfert du système de contrôle en boucle fermée ayant une rétroaction négative unitaire comme
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
Remplacer, $G(s)=\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ dans l'équation ci-dessus.
$$\frac{C(s)}{R(s)}=\frac{\left (\frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}{1+ \left ( \frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}=\frac{\omega _n^2}{s^2+2\delta \omega _ns+\omega _n^2}$$
La puissance du «s» est de deux dans le terme dénominateur. Par conséquent, la fonction de transfert ci-dessus est du second ordre et le système est ditsecond order system.
L'équation caractéristique est -
$$s^2+2\delta \omega _ns+\omega _n^2=0$$
Les racines de l'équation caractéristique sont -
$$s=\frac{-2\omega \delta _n\pm \sqrt{(2\delta\omega _n)^2-4\omega _n^2}}{2}=\frac{-2(\delta\omega _n\pm \omega _n\sqrt{\delta ^2-1})}{2}$$
$$\Rightarrow s=-\delta \omega_n \pm \omega _n\sqrt{\delta ^2-1}$$
- Les deux racines sont imaginaires lorsque δ = 0.
- Les deux racines sont réelles et égales lorsque δ = 1.
- Les deux racines sont réelles mais non égales lorsque δ> 1.
- Les deux racines sont conjuguées complexes lorsque 0 <δ <1.
Nous pouvons écrire $C(s)$ équation comme,
$$C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$$
Où,
C(s) est la transformée de Laplace du signal de sortie, c (t)
R(s) est la transformée de Laplace du signal d'entrée, r (t)
ωn est la fréquence naturelle
δ est le rapport d'amortissement.
Suivez ces étapes pour obtenir la réponse (sortie) du système de second ordre dans le domaine temporel.
Prendre la transformée de Laplace du signal d'entrée, $r(t)$.
Considérez l'équation, $C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$
Remplacer $R(s)$ valeur dans l'équation ci-dessus.
Faire des fractions partielles de $C(s)$ si nécessaire.
Appliquer la transformation de Laplace inverse à $C(s)$.
Réponse échelonnée du système de second ordre
Considérez le signal de pas d'unité comme une entrée du système de second ordre.
La transformée de Laplace du signal de pas unitaire est,
$$R(s)=\frac{1}{s}$$
Nous savons que la fonction de transfert du système de contrôle en boucle fermée du second ordre est,
$$\frac{C(s)}{R(s)}=\frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$
Cas 1: δ = 0
Remplacer, $\delta = 0$ dans la fonction de transfert.
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+\omega_n^2}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )R(s)$$
Remplacer, $R(s) = \frac{1}{s}$ dans l'équation ci-dessus.
$$C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s^2+\omega_n^2)}$$
Appliquez la transformée de Laplace inverse des deux côtés.
$$c(t)=\left ( 1-\cos(\omega_n t) \right )u(t)$$
Ainsi, la réponse en pas unitaire du système de second ordre lorsque $/delta = 0$ sera un signal de temps continu avec une amplitude et une fréquence constantes.
Cas 2: δ = 1
Remplacer, $/delta = 1$ dans la fonction de transfert.
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\omega_ns+\omega_n^2}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)R(s)$$
Remplacer, $R(s) = \frac{1}{s}$ dans l'équation ci-dessus.
$$C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)\left ( \frac{1}{s} \right)=\frac{\omega_n^2}{s(s+\omega_n)^2}$$
Faire des fractions partielles de $C(s)$.
$$C(s)=\frac{\omega_n^2}{s(s+\omega_n)^2}=\frac{A}{s}+\frac{B}{s+\omega_n}+\frac{C}{(s+\omega_n)^2}$$
Après avoir simplifié, vous obtiendrez les valeurs de A, B et C comme $1,\: -1\: and \: −\omega _n$respectivement. Remplacez ces valeurs dans l'expansion de fraction partielle ci-dessus de$C(s)$.
$$C(s)=\frac{1}{s}-\frac{1}{s+\omega_n}-\frac{\omega_n}{(s+\omega_n)^2}$$
Appliquez la transformée de Laplace inverse des deux côtés.
$$c(t)=(1-e^{-\omega_nt}-\omega _nte^{-\omega_nt})u(t)$$
Ainsi, la réponse de pas unitaire du système du second ordre essaiera d'atteindre l'entrée de pas en régime permanent.
Cas 3: 0 <δ <1
On peut modifier le terme dénominateur de la fonction de transfert comme suit -
$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta \omega_n)+(\delta \omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$
$$=(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)$$
La fonction de transfert devient,
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )R(s)$$
Remplacer, $R(s) = \frac{1}{s}$ dans l'équation ci-dessus.
$$C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}$$
Faire des fractions partielles de $C(s)$.
$$C(s)=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}=\frac{A}{s}+\frac{Bs+C}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
Après avoir simplifié, vous obtiendrez les valeurs de A, B et C comme $1,\: -1 \: and \: −2\delta \omega _n$respectivement. Remplacez ces valeurs dans l'expansion de fraction partielle ci-dessus de C (s).
$$C(s)=\frac{1}{s}-\frac{s+2\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$$C(s)=\frac{1}{s}-\frac{s+\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}-\frac{\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_n\sqrt{1-\delta^2}}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2} \right )$
Remplacer, $\omega_n\sqrt{1-\delta^2}$ comme $\omega_d$ dans l'équation ci-dessus.
$$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+\omega_d^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_d}{(s+\delta\omega_n)^2+\omega_d^2} \right )$$
Appliquez la transformée de Laplace inverse des deux côtés.
$$c(t)=\left ( 1-e^{-\delta \omega_nt}\cos(\omega_dt)-\frac{\delta}{\sqrt{1-\delta^2}}e^{-\delta\omega_nt}\sin(\omega_dt) \right )u(t)$$
$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}\left ( (\sqrt{1-\delta^2})\cos(\omega_dt)+\delta \sin(\omega_dt) \right ) \right )u(t)$$
Si $\sqrt{1-\delta^2}=\sin(\theta)$, alors 'δ' sera cos (θ). Remplacez ces valeurs dans l'équation ci-dessus.
$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}(\sin(\theta)\cos(\omega_dt)+\cos(\theta)\sin(\omega_dt)) \right )u(t)$$
$$\Rightarrow c(t)=\left ( 1-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta) \right )u(t)$$
Ainsi, la réponse de pas unitaire du système du second ordre a des oscillations amorties (amplitude décroissante) lorsque «δ» est compris entre zéro et un.
Cas 4: δ> 1
On peut modifier le terme dénominateur de la fonction de transfert comme suit -
$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta\omega_n)+(\delta\omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$
$$=\left ( s+\delta\omega_n \right )^2-\omega_n^2\left ( \delta^2-1 \right )$$
La fonction de transfert devient,
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)}$$
$$\Rightarrow C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)} \right )R(s)$$
Remplacer, $R(s) = \frac{1}{s}$ dans l'équation ci-dessus.
$C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-(\omega_n\sqrt{\delta^2-1})^2} \right )\left ( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$
Faire des fractions partielles de $C(s)$.
$$C(s)=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$$
$$=\frac{A}{s}+\frac{B}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}}+\frac{C}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}}$$
Après avoir simplifié, vous obtiendrez les valeurs de A, B et C comme 1, $\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$ et $\frac{-1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$respectivement. Remplacez ces valeurs dans l'expansion de fraction partielle ci-dessus de$C(s)$.
$$C(s)=\frac{1}{s}+\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}\left ( \frac{1}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}} \right )-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )\left ( \frac{1}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}} \right )$$
Appliquez la transformée de Laplace inverse des deux côtés.
$c(t)=\left ( 1+\left ( \frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t}-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t} \right )u(t)$
Puisqu'elle est suramortie, la réponse de pas unitaire du système du second ordre lorsque δ> 1 n'atteindra jamais l'entrée de pas en régime permanent.
Réponse impulsionnelle du système de second ordre
le impulse response du système du second ordre peut être obtenu en utilisant l'une quelconque de ces deux méthodes.
Suivez la procédure impliquée lors de la dérivation de la réponse par étapes en tenant compte de la valeur de $R(s)$ comme 1 au lieu de $\frac{1}{s}$.
Faites la différenciation de la réponse par étapes.
Le tableau suivant montre la réponse impulsionnelle du système du second ordre pour 4 cas du rapport d'amortissement.
| État du rapport d'amortissement | Réponse impulsionnelle pour t ≥ 0 |
|---|---|
δ = 0 |
$\omega_n\sin(\omega_nt)$ |
δ = 1 |
$\omega_n^2te^{-\omega_nt}$ |
0 <δ <1 |
$\left ( \frac{\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt)$ |
δ> 1 |
$\left ( \frac{\omega_n}{2\sqrt{\delta^2-1}} \right )\left ( e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t}-e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t} \right )$ |
Dans ce chapitre, examinons les spécifications du domaine temporel du système du second ordre. La réponse échelonnée du système de deuxième ordre pour le boîtier sous-amorti est illustrée dans la figure suivante.

Toutes les spécifications du domaine temporel sont représentées sur cette figure. La réponse jusqu'au temps de stabilisation est appelée réponse transitoire et la réponse après le temps de stabilisation est appelée réponse en régime permanent.
Temporisation
C'est le temps nécessaire pour que la réponse atteigne half of its final valueà partir de l'instant zéro. Il est désigné par$t_d$.
Considérons la réponse échelonnée du système du second ordre pour t ≥ 0, lorsque «δ» est compris entre zéro et un.
$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$
La valeur finale de la réponse échelonnée est un.
Par conséquent, à $t=t_d$, la valeur de la réponse échelonnée sera de 0,5. Remplacez ces valeurs dans l'équation ci-dessus.
$$c(t_d)=0.5=1-\left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)$$
$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)=0.5$$
En utilisant l'approximation linéaire, vous obtiendrez le delay time td comme
$$t_d=\frac{1+0.7\delta}{\omega_n}$$
Temps de montée
C'est le temps nécessaire pour que la réponse monte de 0% to 100% of its final value. Ceci est applicable pour leunder-damped systems. Pour les systèmes suramortis, considérez la durée de 10% à 90% de la valeur finale. Le temps de montée est indiqué partr.
À t = t 1 = 0, c (t) = 0.
Nous savons que la valeur finale de la réponse échelonnée est un.
Par conséquent, à $t = t_2$, la valeur de la réponse échelonnée est de un. Remplacez ces valeurs dans l'équation suivante.
$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$
$$c(t_2)=1=1-\left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)$$
$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)=0$$
$$\Rightarrow \sin(\omega_dt_2+\theta)=0$$
$$\Rightarrow \omega_dt_2+\theta=\pi$$
$$\Rightarrow t_2=\frac{\pi-\theta}{\omega_d}$$
Remplacez les valeurs t 1 et t 2 dans l'équation suivante derise time,
$$t_r=t_2-t_1$$
$$\therefore \: t_r=\frac{\pi-\theta}{\omega_d}$$
À partir de l'équation ci-dessus, nous pouvons conclure que le temps de montée $t_r$ et la fréquence amortie $\omega_d$ sont inversement proportionnels les uns aux autres.
Heure de pointe
C'est le temps nécessaire pour que la réponse atteigne le peak valuepour la première fois. Il est désigné par$t_p$. À$t = t_p$, la première dérivée de la réponse est zéro.
Nous savons que la réponse échelonnée du système de second ordre pour le cas sous-amorti est
$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$
Différencier $c(t)$ par rapport à «t».
$$\frac{\text{d}c(t)}{\text{d}t}=-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\omega_d\cos(\omega_dt+\theta)-\left ( \frac{-\delta\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$
Remplacer, $t=t_p$ et $\frac{\text{d}c(t)}{\text{d}t}=0$ dans l'équation ci-dessus.
$$0=-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\left [ \omega_d\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta) \right ]$$
$$\Rightarrow \omega_n\sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta)=0$$
$$\Rightarrow \sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\sin(\omega_dt_p+\theta)=0$$
$$\Rightarrow \sin(\theta)\cos(\omega_dt_p+\theta)-\cos(\theta)\sin(\omega_dt_p+\theta)=0$$
$$\Rightarrow \sin(\theta-\omega_dt_p-\theta)=0$$
$$\Rightarrow sin(-\omega_dt_p)=0\Rightarrow -\sin(\omega_dt_p)=0\Rightarrow sin(\omega_dt_p)=0$$
$$\Rightarrow \omega_dt_p=\pi$$
$$\Rightarrow t_p=\frac{\pi}{\omega_d}$$
À partir de l'équation ci-dessus, nous pouvons conclure que le temps de pointe $t_p$ et la fréquence amortie $\omega_d$ sont inversement proportionnels les uns aux autres.
Dépassement maximal
Dépassement maximal Mpest défini comme l'écart de la réponse à l'heure de pointe par rapport à la valeur finale de la réponse. Il est également appelé lemaximum overshoot.
Mathématiquement, nous pouvons l'écrire comme
$$M_p=c(t_p)-c(\infty)$$
Où,
c (t p ) est la valeur de crête de la réponse.
c (∞) est la valeur finale (état stationnaire) de la réponse.
À $t = t_p$, la réponse c (t) est -
$$c(t_p)=1-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_p+\theta)$$
Remplacer, $t_p=\frac{\pi}{\omega_d}$ dans la partie droite de l'équation ci-dessus.
$$c(t_P)=1-\left ( \frac{e^{-\delta\omega_n\left ( \frac{\pi}{\omega_d} \right )}}{\sqrt{1-\delta^2}} \right )\sin\left ( \omega_d\left ( \frac{\pi}{\omega_d} \right ) +\theta\right )$$
$$\Rightarrow c(t_p)=1-\left ( \frac{e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}}{\sqrt{1-\delta^2}} \right )(-\sin(\theta))$$
Nous savons que
$$\sin(\theta)=\sqrt{1-\delta^2}$$
Alors, nous obtiendrons $c(t_p)$ comme
$$c(t_p)=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$
Remplacez les valeurs de $c(t_p)$ et $c(\infty)$ dans l'équation de dépassement maximal.
$$M_p=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}-1$$
$$\Rightarrow M_p=e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$
Percentage of peak overshoot % $M_p$ peut être calculé en utilisant cette formule.
$$\%M_p=\frac{M_p}{c(\infty )}\times 100\%$$
En substituant les valeurs de $M_p$ et $c(\infty)$ dans la formule ci-dessus, nous obtiendrons le pourcentage du dépassement maximal $\%M_p$ comme
$$\%M_p=\left ( e^ {-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )} \right )\times 100\%$$
À partir de l'équation ci-dessus, nous pouvons conclure que le pourcentage de dépassement maximal $\% M_p$ diminuera si le taux d'amortissement $\delta$ augmente.
Temps de prise
C'est le temps nécessaire pour que la réponse atteigne l'état d'équilibre et reste dans les bandes de tolérance spécifiées autour de la valeur finale. En général, les bandes de tolérance sont de 2% et 5%. Le temps de stabilisation est indiqué par$t_s$.
Le temps de stabilisation pour la bande de tolérance de 5% est de -
$$t_s=\frac{3}{\delta\omega_n}=3\tau$$
Le temps de stabilisation pour la bande de tolérance de 2% est de -
$$t_s=\frac{4}{\delta\omega_n}=4\tau$$
Où, $\tau$ est la constante de temps et est égal à $\frac{1}{\delta\omega_n}$.
Tant le temps de stabilisation $t_s$ et la constante de temps $\tau$ sont inversement proportionnels au taux d'amortissement $\delta$.
Tant le temps de stabilisation $t_s$ et la constante de temps $\tau$sont indépendants du gain du système. Cela signifie que même le gain du système change, le temps de stabilisation$t_s$ et constante de temps $\tau$ ne changera jamais.
Exemple
Trouvons maintenant les spécifications du domaine temporel d'un système de contrôle ayant la fonction de transfert en boucle fermée $\frac{4}{s^2+2s+4}$ lorsque le signal de pas d'unité est appliqué en tant qu'entrée à ce système de commande.
On sait que la forme standard de la fonction de transfert du système de commande en boucle fermée du second ordre comme
$$\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$
En assimilant ces deux fonctions de transfert, nous obtiendrons la fréquence naturelle non amortie $\omega_n$ comme 2 rad / sec et le taux d'amortissement $\delta$ comme 0,5.
Nous connaissons la formule de la fréquence amortie $\omega_d$ comme
$$\omega_d=\omega_n\sqrt{1-\delta^2}$$
Remplacer, $\omega_n$ et $\delta$ valeurs dans la formule ci-dessus.
$$\Rightarrow \omega_d=2\sqrt{1-(0.5)^2}$$
$$\Rightarrow \omega_d=1.732 \: rad/sec$$
Remplacer, $\delta$ valeur dans la relation suivante
$$\theta=\cos^{-1}\delta$$
$$\Rightarrow \theta=\cos^{-1}(0.5)=\frac{\pi}{3}\:rad$$
Remplacez les valeurs nécessaires ci-dessus dans la formule de chaque spécification du domaine temporel et simplifiez afin d'obtenir les valeurs des spécifications du domaine temporel pour une fonction de transfert donnée.
Le tableau suivant présente les formules des spécifications du domaine temporel, la substitution des valeurs nécessaires et les valeurs finales.
| Spécification du domaine temporel | Formule | Substitution de valeurs dans Formula | Valeur finale |
|---|---|---|---|
Temporisation |
$t_d=\frac{1+0.7\delta}{\omega_n}$ |
$t_d=\frac{1+0.7(0.5)}{2}$ |
$t_d$= 0,675 seconde |
Temps de montée |
$t_r=\frac{\pi-\theta}{\omega_d}$ |
$t_r=\frac{\pi-(\frac{\pi}{3})}{1.732}$ |
$t_r$= 1,207 seconde |
Heure de pointe |
$t_p=\frac{\pi}{\omega_d}$ |
$t_p=\frac{\pi}{1.732}$ |
$t_p$= 1,813 seconde |
% Dépassement maximal |
$\%M_p=\left( e^{-\left (\frac{\delta\pi}{\sqrt{1-\delta^2}} \right ) }\right )\times 100\%$ |
$\%M_p=\left( e^{-\left (\frac{0.5\pi}{\sqrt{1-(0.5)^2}} \right ) }\right )\times 100\%$ |
$\% \: M_p$= 16,32% |
Temps de stabilisation pour une bande de tolérance de 2% |
$t_s=\frac{4}{\delta\omega_n}$ |
$t_S=\frac{4}{(0.5)(2)}$ |
$t_s$= 4 secondes |
La déviation de la sortie du système de commande par rapport à la réponse souhaitée pendant l'état d'équilibre est appelée steady state error. Il est représenté comme$e_{ss}$. Nous pouvons trouver une erreur en régime permanent en utilisant le théorème de la valeur finale comme suit.
$$e_{ss}=\lim_{t \to \infty}e(t)=\lim_{s \to 0}sE(s)$$
Où,
E (s) est la transformée de Laplace du signal d'erreur, $e(t)$
Voyons comment trouver les erreurs d'état stationnaire pour les systèmes de contrôle de rétroaction unitaire et de rétroaction non unitaire un par un.
Erreurs d'état stable pour les systèmes de rétroaction Unity
Considérez le schéma fonctionnel suivant du système de contrôle en boucle fermée, qui a une rétroaction négative unitaire.

Où,
- R (s) est la transformée de Laplace du signal d'entrée de référence $r(t)$
- C (s) est la transformée de Laplace du signal de sortie $c(t)$
Nous connaissons la fonction de transfert du système de contrôle en boucle fermée à rétroaction négative unitaire comme
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
$$\Rightarrow C(s)=\frac{R(s)G(s)}{1+G(s)}$$
La sortie du point de sommation est -
$$E(s)=R(s)-C(s)$$
Substitute $C(s)$ value in the above equation.
$$E(s)=R(s)-\frac{R(s)G(s)}{1+G(s)}$$
$$\Rightarrow E(s)=\frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$
$$\Rightarrow E(s)=\frac{R(s)}{1+G(s)}$$
Substitute $E(s)$ value in the steady state error formula
$$e_{ss}=\lim_{s \to 0} \frac{sR(s)}{1+G(s)}$$
The following table shows the steady state errors and the error constants for standard input signals like unit step, unit ramp & unit parabolic signals.
| Input signal | Steady state error $e_{ss}$ | Error constant |
|---|---|---|
unit step signal |
$\frac{1}{1+k_p}$ |
$K_p=\lim_{s \to 0}G(s)$ |
unit ramp signal |
$\frac{1}{K_v}$ |
$K_v=\lim_{s \to 0}sG(s)$ |
unit parabolic signal |
$\frac{1}{K_a}$ |
$K_a=\lim_{s \to 0}s^2G(s)$ |
Where, $K_p$, $K_v$ and $K_a$ are position error constant, velocity error constant and acceleration error constant respectively.
Note − If any of the above input signals has the amplitude other than unity, then multiply corresponding steady state error with that amplitude.
Note − We can’t define the steady state error for the unit impulse signal because, it exists only at origin. So, we can’t compare the impulse response with the unit impulse input as t denotes infinity.
Example
Let us find the steady state error for an input signal $r(t)=\left( 5+2t+\frac{t^2}{2} \right )u(t)$ of unity negative feedback control system with $G(s)=\frac{5(s+4)}{s^2(s+1)(s+20)}$
The given input signal is a combination of three signals step, ramp and parabolic. The following table shows the error constants and steady state error values for these three signals.
| Input signal | Error constant | Steady state error |
|---|---|---|
$r_1(t)=5u(t)$ |
$K_p=\lim_{s \to 0}G(s)=\infty$ |
$e_{ss1}=\frac{5}{1+k_p}=0$ |
$r_2(t)=2tu(t)$ |
$K_v=\lim_{s \to 0}sG(s)=\infty$ |
$e_{ss2}=\frac{2}{K_v}=0$ |
$r_3(t)=\frac{t^2}{2}u(t)$ |
$K_a=\lim_{s \to 0}s^2G(s)=1$ |
$e_{ss3}=\frac{1}{k_a}=1$ |
We will get the overall steady state error, by adding the above three steady state errors.
$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$
$$\Rightarrow e_{ss}=0+0+1=1$$
Therefore, we got the steady state error $e_{ss}$ as 1 for this example.
Steady State Errors for Non-Unity Feedback Systems
Consider the following block diagram of closed loop control system, which is having nonunity negative feedback.

We can find the steady state errors only for the unity feedback systems. So, we have to convert the non-unity feedback system into unity feedback system. For this, include one unity positive feedback path and one unity negative feedback path in the above block diagram. The new block diagram looks like as shown below.

Simplify the above block diagram by keeping the unity negative feedback as it is. The following is the simplified block diagram.

This block diagram resembles the block diagram of the unity negative feedback closed loop control system. Here, the single block is having the transfer function $\frac{G(s)}{1+G(s)H(s)-G(s)}$ instead of $G(s)$. You can now calculate the steady state errors by using steady state error formula given for the unity negative feedback systems.
Note − It is meaningless to find the steady state errors for unstable closed loop systems. So, we have to calculate the steady state errors only for closed loop stable systems. This means we need to check whether the control system is stable or not before finding the steady state errors. In the next chapter, we will discuss the concepts-related stability.
Stability is an important concept. In this chapter, let us discuss the stability of system and types of systems based on stability.
What is Stability?
A system is said to be stable, if its output is under control. Otherwise, it is said to be unstable. A stable system produces a bounded output for a given bounded input.
The following figure shows the response of a stable system.

C'est la réponse du système de commande de premier ordre pour l'entrée de pas d'unité. Cette réponse a les valeurs comprises entre 0 et 1. Il s'agit donc d'une sortie bornée. Nous savons que le signal de pas unitaire a la valeur de un pour toutes les valeurs positives dety compris zéro. Donc, c'est une entrée bornée. Par conséquent, le système de commande du premier ordre est stable car à la fois l'entrée et la sortie sont limitées.
Types de systèmes basés sur la stabilité
Nous pouvons classer les systèmes en fonction de la stabilité comme suit.
- Système absolument stable
- Système conditionnellement stable
- Système marginalement stable
Système absolument stable
Si le système est stable pour toute la plage de valeurs des composants du système, il est appelé absolutely stable system. Le système de contrôle en boucle ouverte est absolument stable si tous les pôles de la fonction de transfert en boucle ouverte sont présents dans la moitié gauche de‘s’ plane. De même, le système de contrôle en boucle fermée est absolument stable si tous les pôles de la fonction de transfert en boucle fermée sont présents dans la moitié gauche du plan «s».
Système conditionnellement stable
Si le système est stable pour une certaine plage de valeurs de composants système, il est appelé conditionally stable system.
Système marginalement stable
Si le système est stable en produisant un signal de sortie avec une amplitude et une fréquence d'oscillations constantes pour une entrée limitée, alors il est connu comme marginally stable system. Le système de commande en boucle ouverte est légèrement stable si deux pôles quelconques de la fonction de transfert en boucle ouverte sont présents sur l'axe imaginaire. De même, le système de commande en boucle fermée est marginalement stable si deux pôles quelconques de la fonction de transfert en boucle fermée sont présents sur l'axe imaginaire.
Dans ce chapitre, discutons de l'analyse de stabilité dans le ‘s’domaine utilisant le critère de stabilité de RouthHurwitz. Dans ce critère, nous avons besoin de l'équation caractéristique pour trouver la stabilité des systèmes de contrôle en boucle fermée.
Critère de stabilité de Routh-Hurwitz
Le critère de stabilité de Routh-Hurwitz est d'avoir une condition nécessaire et une condition suffisante pour la stabilité. Si un système de contrôle ne satisfait pas à la condition nécessaire, alors nous pouvons dire que le système de contrôle est instable. Mais, si le système de contrôle satisfait à la condition nécessaire, il peut être stable ou non. Ainsi, la condition suffisante est utile pour savoir si le système de contrôle est stable ou non.
Condition nécessaire à la stabilité Routh-Hurwitz
La condition nécessaire est que les coefficients du polynôme caractéristique soient positifs. Cela implique que toutes les racines de l'équation caractéristique doivent avoir des parties réelles négatives.
Considérons l'équation caractéristique de l'ordre 'n' est -
$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0=0$$
Notez qu'il ne devrait pas y avoir de terme manquant dans le nthordre de l'équation caractéristique. Cela signifie que lenth L'équation caractéristique d'ordre ne doit avoir aucun coefficient de valeur nulle.
Condition suffisante pour la stabilité Routh-Hurwitz
La condition suffisante est que tous les éléments de la première colonne du tableau Routh doivent avoir le même signe. Cela signifie que tous les éléments de la première colonne du tableau Routh doivent être positifs ou négatifs.
Méthode Routh Array
Si toutes les racines de l'équation caractéristique existent dans la moitié gauche du plan «s», alors le système de contrôle est stable. Si au moins une racine de l'équation caractéristique existe dans la moitié droite du plan «s», alors le système de contrôle est instable. Il faut donc trouver les racines de l'équation caractéristique pour savoir si le système de contrôle est stable ou instable. Mais, il est difficile de trouver les racines de l'équation caractéristique à mesure que l'ordre augmente.
Donc, pour surmonter ce problème, nous avons le Routh array method. Dans cette méthode, il n'est pas nécessaire de calculer les racines de l'équation caractéristique. Formulez d'abord la table Routh et recherchez le nombre de changements de signe dans la première colonne de la table Routh. Le nombre de changements de signe dans la première colonne du tableau de Routh donne le nombre de racines de l'équation caractéristique qui existent dans la moitié droite du plan «s» et le système de contrôle est instable.
Suivez cette procédure pour former la table Routh.
Remplissez les deux premières lignes du tableau Routh avec les coefficients du polynôme caractéristique comme indiqué dans le tableau ci-dessous. Commencez par le coefficient de$s^n$ et continuer jusqu'au coefficient de $s^0$.
Remplissez les lignes restantes du tableau Routh avec les éléments comme indiqué dans le tableau ci-dessous. Continuez ce processus jusqu'à ce que vous obteniez le premier élément de colonne derow $s^0$ est $a_n$. Ici,$a_n$ est le coefficient de $s^0$ dans le polynôme caractéristique.
Note - Si des éléments de ligne de la table Routh ont un facteur commun, vous pouvez diviser les éléments de ligne avec ce facteur pour que la simplification soit facile.
Le tableau suivant montre le tableau de Routh du n ième ordre polynomial caractéristique.
$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0$$
$s^n$ |
$a_0$ |
$a_2$ |
$a_4$ |
$a_6$ |
... |
... |
$s^{n-1}$ |
$a_1$ |
$a_3$ |
$a_5$ |
$a_7$ |
... |
... |
$s^{n-2}$ |
$b_1=\frac{a_1a_2-a_3a_0}{a_1}$ |
$b_2=\frac{a_1a_4-a_5a_0}{a_1}$ |
$b_3=\frac{a_1a_6-a_7a_0}{a_1}$ |
... |
... |
... |
$s^{n-3}$ |
$c_1=\frac{b_1a_3-b_2a_1}{b_1}$ |
$c_2=\frac{b_1a_55-b_3a_1}{b_1}$ |
$\vdots$ |
|||
$\vdots $ |
$\vdots$ |
$\vdots$ |
$\vdots$ |
|||
$s^1$ |
$\vdots$ |
$\vdots$ |
||||
$s^0$ |
$a_n$ |
Example
Trouvons la stabilité du système de contrôle ayant l'équation caractéristique,
$$s^4+3s^3+3s^2+2s+1=0$$
Step 1 - Vérifier les conditions nécessaires à la stabilité du Routh-Hurwitz.
Tous les coefficients du polynôme caractéristique, $s^4+3s^3+3s^2+2s+1$sont positifs. Ainsi, le système de contrôle remplit la condition nécessaire.
Step 2 - Former le tableau de Routh pour le polynôme caractéristique donné.
$s^4$ |
$1$ |
$3$ |
$1$ |
$s^3$ |
$3$ |
$2$ |
|
$s^2$ |
$\frac{(3 \times 3)-(2 \times 1)}{3}=\frac{7}{3}$ |
$\frac{(3 \times 1)-(0 \times 1)}{3}=\frac{3}{3}=1$ |
|
$s^1$ |
$\frac{\left ( \frac{7}{3}\times 2 \right )-(1 \times 3)}{\frac{7}{3}}=\frac{5}{7}$ |
||
$s^0$ |
$1$ |
Step 3 - Vérifier les conditions suffisantes pour la stabilité Routh-Hurwitz.
Tous les éléments de la première colonne du tableau Routh sont positifs. Il n'y a pas de changement de signe dans la première colonne du tableau Routh. Ainsi, le système de contrôle est stable.
Cas particuliers de Routh Array
On peut rencontrer deux types de situations, en formant la table de Routh. Il est difficile de compléter le tableau de Routh à partir de ces deux situations.
Les deux cas particuliers sont -
- Le premier élément de toute ligne du tableau Routh est zéro.
- Tous les éléments de n'importe quelle ligne du tableau Routh sont nuls.
Voyons maintenant comment surmonter la difficulté dans ces deux cas, un par un.
Le premier élément de n'importe quelle ligne du tableau Routh est zéro
Si une ligne du tableau Routh contient uniquement le premier élément comme zéro et au moins un des éléments restants a une valeur non nulle, remplacez le premier élément par un petit entier positif, $\epsilon$. Et puis continuez le processus pour compléter la table Routh. Maintenant, trouvez le nombre de changements de signe dans la première colonne du tableau Routh en remplaçant$\epsilon$ tend vers zéro.
Example
Trouvons la stabilité du système de contrôle ayant l'équation caractéristique,
$$s^4+2s^3+s^2+2s+1=0$$
Step 1 - Vérifier les conditions nécessaires à la stabilité du Routh-Hurwitz.
Tous les coefficients du polynôme caractéristique, $s^4+2s^3+s^2+2s+1$sont positifs. Ainsi, le système de contrôle a satisfait à la condition nécessaire.
Step 2 - Former le tableau de Routh pour le polynôme caractéristique donné.
$s^4$ |
$1$ |
$1$ |
$1$ |
$s^3$ |
|
|
|
$s^2$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
$\frac{(1 \times 1)-(0 \times 1)}{1}=1$ |
|
$s^1$ |
|||
$s^0$ |
La ligne $s^3$les éléments ont 2 comme facteur commun. Donc, tous ces éléments sont divisés par 2.
Special case (i) - Seul le premier élément de la ligne $s^2$est zéro. Alors, remplacez-le par$\epsilon$ et continuez le processus pour compléter le tableau de Routh.
$s^4$ |
1 |
1 |
1 |
$s^3$ |
1 |
1 |
|
$s^2$ |
$\epsilon$ |
1 |
|
$s^1$ |
$\frac{\left ( \epsilon \times 1 \right )-\left ( 1 \times 1 \right )}{\epsilon}=\frac{\epsilon-1}{\epsilon}$ |
||
$s^0$ |
1 |
Step 3 - Vérifier les conditions suffisantes pour la stabilité Routh-Hurwitz.
Comme $\epsilon$ tend vers zéro, la table Routh devient ainsi.
$s^4$ |
1 |
1 |
1 |
$s^3$ |
1 |
1 |
|
$s^2$ |
0 |
1 |
|
$s^1$ |
-∞ |
||
$s^0$ |
1 |
Il y a deux changements de signe dans la première colonne du tableau Routh. Par conséquent, le système de contrôle est instable.
Tous les éléments de n'importe quelle ligne du tableau Routh sont nuls
Dans ce cas, suivez ces deux étapes -
Écrivez l'équation auxiliaire, A (s) de la ligne, qui est juste au-dessus de la ligne de zéros.
Différencier l'équation auxiliaire, A (s) par rapport à s. Remplissez la rangée de zéros avec ces coefficients.
Example
Trouvons la stabilité du système de contrôle ayant l'équation caractéristique,
$$s^5+3s^4+s^3+3s^2+s+3=0$$
Step 1 - Vérifier les conditions nécessaires à la stabilité du Routh-Hurwitz.
Tous les coefficients du polynôme caractéristique donné sont positifs. Ainsi, le système de contrôle a satisfait à la condition nécessaire.
Step 2 - Former le tableau de Routh pour le polynôme caractéristique donné.
$s^5$ |
1 |
1 |
1 |
$s^4$ |
|
|
|
$s^3$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
|
$s^2$ |
|||
$s^1$ |
|||
$s^0$ |
La ligne $s^4$ les éléments ont le facteur commun de 3. Donc, tous ces éléments sont divisés par 3.
Special case (ii) - Tous les éléments de ligne $s^3$sont nuls. Alors, écrivez l'équation auxiliaire, A (s) de la ligne$s^4$.
$$A(s)=s^4+s^2+1$$
Différenciez l'équation ci-dessus par rapport à l'art.
$$\frac{\text{d}A(s)}{\text{d}s}=4s^3+2s$$
Placez ces coefficients en ligne $s^3$.
$s^5$ |
1 |
1 |
1 |
$s^4$ |
1 |
1 |
1 |
$s^3$ |
|
|
|
$s^2$ |
$\frac{(2 \times 1)-(1 \times 1)}{2}=0.5$ |
$\frac{(2 \times 1)-(0 \times 1)}{2}=1$ |
|
$s^1$ |
$\frac{(0.5 \times 1)-(1 \times 2)}{0.5}=\frac{-1.5}{0.5}=-3$ |
||
$s^0$ |
1 |
Step 3 - Vérifier les conditions suffisantes pour la stabilité Routh-Hurwitz.
Il y a deux changements de signe dans la première colonne du tableau Routh. Par conséquent, le système de contrôle est instable.
Dans le critère de stabilité de Routh-Hurwitz, nous pouvons savoir si les pôles en boucle fermée sont dans la moitié gauche du plan «s» ou sur la moitié droite du plan «s» ou sur un axe imaginaire. Donc, nous ne pouvons pas trouver la nature du système de contrôle. Pour surmonter cette limitation, il existe une technique connue sous le nom de locus racine. Nous discuterons de cette technique dans les deux prochains chapitres.
Dans le diagramme de locus racine, nous pouvons observer le chemin des pôles en boucle fermée. Par conséquent, nous pouvons identifier la nature du système de contrôle. Dans cette technique, nous utiliserons une fonction de transfert en boucle ouverte pour connaître la stabilité du système de contrôle en boucle fermée.
Bases du locus racine
Le locus racine est le lieu des racines de l'équation caractéristique en faisant varier le gain système K de zéro à l'infini.
On sait que l'équation caractéristique du système de contrôle en boucle fermée est
$$1+G(s)H(s)=0$$
Nous pouvons représenter $G(s)H(s)$ comme
$$G(s)H(s)=K\frac{N(s)}{D(s)}$$
Où,
K représente le facteur multiplicateur
N (s) représente le terme numérateur ayant (factorisé) le polynôme d'ordre n de «s».
D (s) représente le terme dénominateur ayant (factorisé) le polynôme d'ordre m de «s».
Remplacer, $G(s)H(s)$ valeur dans l'équation caractéristique.
$$1+k\frac{N(s)}{D(s)}=0$$
$$\Rightarrow D(s)+KN(s)=0$$
Case 1 − K = 0
Si $K=0$, puis $D(s)=0$.
Cela signifie que les pôles en boucle fermée sont égaux aux pôles en boucle ouverte lorsque K est égal à zéro.
Case 2 − K = ∞
Réécrivez l'équation caractéristique ci-dessus comme
$$K\left(\frac{1}{K}+\frac{N(s)}{D(s)} \right )=0 \Rightarrow \frac{1}{K}+\frac{N(s)}{D(s)}=0$$
Remplacer, $K = \infty$ dans l'équation ci-dessus.
$$\frac{1}{\infty}+\frac{N(s)}{D(s)}=0 \Rightarrow \frac{N(s)}{D(s)}=0 \Rightarrow N(s)=0$$
Si $K=\infty$, puis $N(s)=0$. Cela signifie que les pôles de la boucle fermée sont égaux aux zéros de la boucle ouverte lorsque K est l'infini.
À partir de deux cas ci-dessus, nous pouvons conclure que les branches du locus racine commencent aux pôles en boucle ouverte et se terminent aux zéros en boucle ouverte.
Condition d'angle et condition d'amplitude
Les points sur les branches du locus racine satisfont la condition d'angle. Ainsi, la condition d'angle est utilisée pour savoir si le point existe ou non sur la branche du locus racine. Nous pouvons trouver la valeur de K pour les points sur les branches du locus racine en utilisant la condition de magnitude. Ainsi, nous pouvons utiliser la condition de magnitude pour les points, et cela satisfait la condition d'angle.
L'équation caractéristique du système de contrôle en boucle fermée est
$$1+G(s)H(s)=0$$
$$\Rightarrow G(s)H(s)=-1+j0$$
le phase angle de $G(s)H(s)$ est
$$\angle G(s)H(s)=\tan^{-1}\left ( \frac{0}{-1} \right )=(2n+1)\pi$$
le angle conditionest le point auquel l'angle de la fonction de transfert en boucle ouverte est un multiple impair de 180 0 .
Magnitude de $G(s)H(s)$ est -
$$|G(s)H(s)|=\sqrt {(-1)^2+0^2}=1$$
La condition de grandeur est le point (qui satisfait la condition d'angle) auquel la grandeur de la fonction de transfert en boucle ouverte est un.
le root locusest une représentation graphique dans le domaine s et elle est symétrique par rapport à l'axe réel. Parce que les pôles et les zéros en boucle ouverte existent dans le domaine s ayant les valeurs sous forme de paires conjuguées réelles ou complexes. Dans ce chapitre, discutons de la façon de construire (dessiner) le locus racine.
Règles de construction du locus racine
Suivez ces règles pour construire un locus racine.
Rule 1 - Localisez les pôles de la boucle ouverte et les zéros dans le plan 's'.
Rule 2 - Trouvez le nombre de branches du locus racine.
Nous savons que les branches du locus racine commencent aux pôles de la boucle ouverte et se terminent aux zéros de la boucle ouverte. Donc, le nombre de branches du locus racineN est égal au nombre de pôles finis en boucle ouverte P ou le nombre de zéros finis en boucle ouverte Z, selon la valeur la plus élevée.
Mathématiquement, nous pouvons écrire le nombre de branches du locus racine N comme
$N=P$ si $P\geq Z$
$N=Z$ si $P<Z$
Rule 3 - Identifiez et dessinez le real axis root locus branches.
Si l'angle de la fonction de transfert en boucle ouverte en un point est un multiple impair de 180 0 , alors ce point est sur le lieu racine. S'il existe un nombre impair de pôles en boucle ouverte et des zéros sur le côté gauche d'un point sur l'axe réel, alors ce point se trouve sur la branche du locus racine. Par conséquent, la branche de points qui satisfait à cette condition est l'axe réel de la branche du locus racine.
Rule 4 - Trouvez le centre de gravité et l'angle des asymptotes.
Si $P = Z$, alors toutes les branches du locus racine commencent à des pôles finis en boucle ouverte et se terminent à des zéros finis en boucle ouverte.
Si $P > Z$ , puis $Z$ nombre de branches de locus racine commencent aux pôles finis en boucle ouverte et se terminent aux zéros finis en boucle ouverte et $P − Z$ Le nombre de branches de locus racine commence à des pôles de boucle ouverte finis et se termine à des zéros en boucle ouverte infinis.
Si $P < Z$ , alors le nombre P de branches de locus racine commence aux pôles finis en boucle ouverte et se termine aux zéros finis en boucle ouverte et $Z − P$ nombre de branches de locus racine commencent à des pôles en boucle ouverte infinis et se terminent à des zéros en boucle ouverte finie.
Ainsi, certaines branches du locus racine se rapprochent de l'infini, lorsque $P \neq Z$. Les asymptotes donnent la direction de ces branches du locus racinaire. Le point d'intersection des asymptotes sur l'axe réel est appelécentroid.
Nous pouvons calculer le centroid α en utilisant cette formule,
$\alpha = \frac{\sum Real\: part\: of\: finite\: open\: loop\: poles\:-\sum Real\: part\: of\: finite\: open\: loop\: zeros}{P-Z}$
La formule de l'angle de asymptotes θ est
$$\theta=\frac{(2q+1)180^0}{P-Z}$$
Où,
$$q=0,1,2,....,(P-Z)-1$$
Rule 5 - Trouvez les points d'intersection des branches du locus racine avec un axe imaginaire.
Nous pouvons calculer le point auquel la branche du locus racine coupe l'axe imaginaire et la valeur de K à ce stade en utilisant la méthode de tableau Routh et case (ii).
Si tous les éléments d'une ligne quelconque du tableau Routh sont égaux à zéro, alors la branche du locus racine coupe l'axe imaginaire et vice-versa.
Identifiez la ligne de telle manière que si nous rendons le premier élément égal à zéro, les éléments de la ligne entière soient à zéro. Trouvez la valeur deK pour cette combinaison.
Remplacez ceci Kvaleur dans l'équation auxiliaire. Vous obtiendrez le point d'intersection de la branche du locus racine avec un axe imaginaire.
Rule 6 - Trouvez des points de rupture et de rupture.
S'il existe une branche de locus racine d'axe réel entre deux pôles en boucle ouverte, alors il y aura un break-away point entre ces deux pôles en boucle ouverte.
S'il existe une branche de locus racine d'axe réel entre deux zéros en boucle ouverte, alors il y aura un break-in point entre ces deux zéros en boucle ouverte.
Note - Les points de rupture et de rupture n'existent que sur les branches du locus racine de l'axe réel.
Suivez ces étapes pour trouver les points de rupture et de rodage.
Écrire $K$ en terme de $s$ de l'équation caractéristique $1 + G(s)H(s) = 0$.
Différencier $K$par rapport à s et le rendre égal à zéro. Remplacez ces valeurs par$s$ dans l'équation ci-dessus.
Les valeurs de $s$ pour lequel le $K$ la valeur est positive sont les break points.
Rule 7 - Trouvez l'angle de départ et l'angle d'arrivée.
L'angle de départ et l'angle d'arrivée peuvent être calculés respectivement à des pôles en boucle ouverte conjugués complexes et à des zéros en boucle ouverte conjugués complexes.
La formule pour le angle of departure $\phi_d$ est
$$\phi_d=180^0-\phi$$
La formule pour le angle of arrival $\phi_a$ est
$$\phi_a=180^0+\phi$$
Où,
$$\phi=\sum \phi_P-\sum \phi_Z$$
Exemple
Trouvons maintenant le locus racine du système de contrôle ayant une fonction de transfert en boucle ouverte, $G(s)H(s)=\frac{K}{s(s+1)(s+5)}$
Step 1 - La fonction de transfert en boucle ouverte donnée a trois pôles à $s = 0, s = −1$ et $s = −5$. Il n'a pas de zéro. Par conséquent, le nombre de branches de locus racine est égal au nombre de pôles de la fonction de transfert en boucle ouverte.
$$N=P=3$$

Les trois pôles situés sont illustrés dans la figure ci-dessus. Le segment de ligne entre$s = −1$ et $s = 0$est une branche du locus racine sur l'axe réel. Et l'autre branche du locus racine sur l'axe réel est le segment de ligne à gauche de$s = −5$.
Step 2 - Nous obtiendrons les valeurs du centroïde et de l'angle des asymptotes en utilisant les formules données.
Centroïde $\alpha = −2$
L'angle des asymptotes est $\theta = 60^0,180^0$ et $300^0$.
Le centre de gravité et trois asymptotes sont indiqués dans la figure suivante.

Step 3 - Puisque deux asymptotes ont les angles de $60^0$ et $300^0$, deux branches de locus racine coupent l'axe imaginaire. En utilisant la méthode du tableau de Routh et le cas spécial (ii), les branches du locus racine coupent l'axe imaginaire à$j\sqrt{5}$ et $−j\sqrt{5}$.
Il y aura un point de rupture sur la branche du locus racine de l'axe réel entre les pôles $s = −1$ et $s = 0$. En suivant la procédure donnée pour le calcul du point de rupture, nous l'obtiendrons comme$s = −0.473$.
Le diagramme du locus racine pour le système de contrôle donné est illustré dans la figure suivante.

De cette façon, vous pouvez dessiner le diagramme du lieu racine de n'importe quel système de contrôle et observer le mouvement des pôles de la fonction de transfert en boucle fermée.
À partir des diagrammes de locus racine, nous pouvons connaître la plage de valeurs K pour différents types d'amortissement.
Effets de l'ajout de pôles en boucle ouverte et de zéros sur le locus racine
Le locus racine peut être déplacé en ‘s’ plane en ajoutant les pôles en boucle ouverte et les zéros en boucle ouverte.
Si nous incluons un pôle dans la fonction de transfert en boucle ouverte, alors certaines des branches du locus racine se déplaceront vers la moitié droite du plan «s». Pour cette raison, le rapport d'amortissement$\delta$diminue. Ce qui implique, fréquence amortie$\omega_d$ augmente et les spécifications du domaine temporel comme le temps de retard $t_d$, temps de montée $t_r$ et heure de pointe $t_p$diminution. Mais cela affecte la stabilité du système.
Si nous incluons un zéro dans la fonction de transfert en boucle ouverte, alors certaines des branches du locus racine se déplaceront vers la moitié gauche du plan «s». Ainsi, cela augmentera la stabilité du système de contrôle. Dans ce cas, le taux d'amortissement$\delta$augmente. Ce qui implique, fréquence amortie$\omega_d$ diminue et les spécifications du domaine temporel comme le temps de retard $t_d$, temps de montée $t_r$ et heure de pointe $t_p$ augmenter.
Ainsi, en fonction de l'exigence, nous pouvons inclure (ajouter) les pôles en boucle ouverte ou les zéros à la fonction de transfert.
Nous avons déjà discuté de l'analyse de la réponse temporelle des systèmes de contrôle et des spécifications du domaine temporel des systèmes de contrôle du second ordre. Dans ce chapitre, discutons de l'analyse de la réponse en fréquence des systèmes de commande et des spécifications du domaine fréquentiel des systèmes de commande du second ordre.
Qu'est-ce que la réponse en fréquence?
La réponse d'un système peut être partitionnée à la fois en réponse transitoire et en réponse en régime permanent. Nous pouvons trouver la réponse transitoire en utilisant des intégrales de Fourier. La réponse en régime permanent d'un système pour un signal sinusoïdal d'entrée est connue sous le nom defrequency response. Dans ce chapitre, nous nous concentrerons uniquement sur la réponse en régime permanent.
Si un signal sinusoïdal est appliqué en tant qu'entrée à un système linéaire invariant dans le temps (LTI), il produit alors la sortie en régime permanent, qui est également un signal sinusoïdal. Les signaux sinusoïdaux d'entrée et de sortie ont la même fréquence, mais des amplitudes et des angles de phase différents.
Soit le signal d'entrée -
$$r(t)=A\sin(\omega_0t)$$
La fonction de transfert en boucle ouverte sera -
$$G(s)=G(j\omega)$$
Nous pouvons représenter $G(j\omega)$ en termes d'amplitude et de phase comme indiqué ci-dessous.
$$G(j\omega)=|G(j\omega)| \angle G(j\omega)$$
Remplacer, $\omega = \omega_0$ dans l'équation ci-dessus.
$$G(j\omega_0)=|G(j\omega_0)| \angle G(j\omega_0)$$
Le signal de sortie est
$$c(t)=A|G(j\omega_0)|\sin(\omega_0t + \angle G(j\omega_0))$$
le amplitude du signal sinusoïdal de sortie est obtenu en multipliant l'amplitude du signal sinusoïdal d'entrée et l'amplitude de $G(j\omega)$ à $\omega = \omega_0$.
le phase du signal sinusoïdal de sortie est obtenu en additionnant la phase du signal sinusoïdal d'entrée et la phase de $G(j\omega)$ à $\omega = \omega_0$.
Où,
A est l'amplitude du signal sinusoïdal d'entrée.
ω0 est la fréquence angulaire du signal sinusoïdal d'entrée.
On peut écrire, fréquence angulaire $\omega_0$ comme indiqué ci-dessous.
$$\omega_0=2\pi f_0$$
Ici, $f_0$est la fréquence du signal sinusoïdal d'entrée. De même, vous pouvez suivre la même procédure pour le système de contrôle en boucle fermée.
Spécifications du domaine de fréquence
Les spécifications du domaine fréquentiel sont resonant peak, resonant frequency and bandwidth.
Considérons la fonction de transfert du système de contrôle en boucle fermée du second ordre comme,
$$T(s)=\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$
Remplacer, $s = j\omega$ dans l'équation ci-dessus.
$$T(j\omega)=\frac{\omega_n^2}{(j\omega)^2+2\delta\omega_n(j\omega)+\omega_n^2}$$
$$\Rightarrow T(j\omega)=\frac{\omega_n^2}{-\omega^2+2j\delta\omega\omega_n+\omega_n^2}=\frac{\omega_n^2}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$$
$$\Rightarrow T(j\omega)=\frac{1}{\left ( 1-\frac{\omega^2}{\omega_n^2} \right )+j\left ( \frac{2\delta\omega}{\omega_n} \right )}$$
Laisser, $\frac{\omega}{\omega_n}=u$ Remplacez cette valeur dans l'équation ci-dessus.
$$T(j\omega)=\frac{1}{(1-u^2)+j(2\delta u)}$$
Magnitude de $T(j\omega)$ est -
$$M=|T(j\omega)|=\frac{1}{\sqrt {(1-u^2)^2+(2\delta u)^2}}$$
Phase de $T(j\omega)$ est -
$$\angle T(j\omega)=-tan^{-1}\left( \frac{2\delta u}{1-u^2} \right )$$
Fréquence de résonance
C'est la fréquence à laquelle l'amplitude de la réponse en fréquence a une valeur de crête pour la première fois. Il est désigné par$\omega_r$. À$\omega = \omega_r$, la première dérivée de la grandeur de $T(j\omega)$ est zéro.
Différencier $M$ par rapport à $u$.
$$\frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [2(1-u^2)(-2u)+2(2\delta u)(2\delta) \right ]$$
$$\Rightarrow \frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [4u(u^2-1 +2\delta^2) \right ]$$
Remplacer, $u=u_r$ et $\frac{\text{d}M}{\text{d}u}==0$ dans l'équation ci-dessus.
$$0=-\frac{1}{2}\left [ (1-u_r^2)^2+(2\delta u_r)^2 \right ]^{-\frac{3}{2}}\left [ 4u_r(u_r^2-1 +2\delta^2) \right ]$$
$$\Rightarrow 4u_r(u_r^2-1 +2\delta^2)=0$$
$$\Rightarrow u_r^2-1+2\delta^2=0$$
$$\Rightarrow u_r^2=1-2\delta^2$$
$$\Rightarrow u_r=\sqrt{1-2\delta^2}$$
Remplacer, $u_r=\frac{\omega_r}{\omega_n}$ dans l'équation ci-dessus.
$$\frac{\omega_r}{\omega_n}=\sqrt{1-2\delta^2}$$
$$\Rightarrow \omega_r=\omega_n \sqrt{1-2\delta^2}$$
Pic résonnant
C'est la valeur maximale (maximale) de la magnitude de $T(j\omega)$. Il est désigné par$M_r$.
À $u = u_r$, l'ampleur de $T(j\omega)$ est -
$$M_r=\frac{1}{\sqrt{(1-u_r^2)^2+(2\delta u_r)^2}}$$
Remplacer, $u_r = \sqrt{1 − 2\delta^2}$ et $1 − u_r^2 = 2\delta^2$ dans l'équation ci-dessus.
$$M_r=\frac{1}{\sqrt{(2\delta^2)^2+(2\delta \sqrt{1-2\delta^2})^2}}$$
$$\Rightarrow M_r=\frac{1}{2\delta \sqrt {1-\delta^2}}$$
Le pic de résonance de la réponse en fréquence correspond au dépassement de pic de la réponse transitoire du domaine temporel pour certaines valeurs du rapport d'amortissement $\delta$. Ainsi, le pic de résonance et le dépassement de pic sont corrélés l'un à l'autre.
Bande passante
C'est la gamme de fréquences sur laquelle, la magnitude de $T(j\omega)$ tombe à 70,7% de sa valeur de fréquence zéro.
À $\omega = 0$, la valeur de $u$ sera nul.
Remplacer, $u = 0$ dans M.
$$M=\frac{1}{\sqrt {(1-0^2)^2+(2\delta(0))^2}}=1$$
Par conséquent, l'ampleur de $T(j\omega)$ est un à $\omega = 0$.
À une fréquence de 3 dB, l'amplitude de $T(j\omega)$ sera 70,7% de la magnitude de $T(j\omega)$ à $\omega = 0$.
je mange $\omega = \omega_B, M = 0.707(1) = \frac{1}{\sqrt{2}}$
$$\Rightarrow M=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{(1-u_b^2)^2+(2\delta u_b)^2}}$$
$$\Rightarrow 2=(1-u_b^2)^2+(2\delta)^2 u_b^2$$
Laisser, $u_b^2=x$
$$\Rightarrow 2=(1-x)^2+(2\delta)^2 x$$
$$\Rightarrow x^2+(4\delta^2-2)x-1=0$$
$$\Rightarrow x=\frac{-(4\delta^2 -2)\pm \sqrt{(4\delta^2-2)^2+4}}{2}$$
Considérez uniquement la valeur positive de x.
$$x=1-2\delta^2+\sqrt {(2\delta^2-1)^2+1}$$
$$\Rightarrow x=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$
Remplacer, $x=u_b^2=\frac{\omega_b^2}{\omega_n^2}$
$$\frac{\omega_b^2}{\omega_n^2}=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$
$$\Rightarrow \omega_b=\omega_n \sqrt {1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}}$$
Bande passante $\omega_b$ dans la réponse en fréquence est inversement proportionnelle au temps de montée $t_r$ dans le domaine temporel de la réponse transitoire.
Le tracé de Bode ou le diagramme de Bode se compose de deux tracés -
- Graphique de magnitude
- Diagramme de phase
Dans les deux graphiques, l'axe des x représente la fréquence angulaire (échelle logarithmique). Alors que l'axe y représente la magnitude (échelle linéaire) de la fonction de transfert en boucle ouverte dans le tracé d'amplitude et l'angle de phase (échelle linéaire) de la fonction de transfert en boucle ouverte dans le tracé de phase.
le magnitude de la fonction de transfert en boucle ouverte en dB est -
$$M=20\: \log|G(j\omega)H(j\omega)|$$
le phase angle de la fonction de transfert en boucle ouverte en degrés est -
$$\phi=\angle G(j\omega)H(j\omega)$$
Note - La base du logarithme est 10.
Bases des graphiques de Bode
Le tableau suivant montre la pente, l'amplitude et les valeurs d'angle de phase des termes présents dans la fonction de transfert en boucle ouverte. Ces données sont utiles lors du dessin des tracés de Bode.
| Type de terme | G (jω) H (jω) | Pente (dB / déc) | Magnitude (dB) | Angle de phase (degrés) |
|---|---|---|---|---|
Constant |
$K$ |
$0$ |
$20 \log K$ |
$0$ |
Zéro à l'origine |
$j\omega$ |
$20$ |
$20 \log \omega$ |
$90$ |
'n' zéros à l'origine |
$(j\omega)^n$ |
$20\: n$ |
$20\: n \log \omega$ |
$90\: n$ |
Pôle à l'origine |
$\frac{1}{j\omega}$ |
$-20$ |
$-20 \log \omega$ |
$-90 \: or \: 270$ |
'n' pôles à l'origine |
$\frac{1}{(j\omega)^n}$ |
$-20\: n$ |
$-20 \: n \log \omega$ |
$-90 \: n \: or \: 270 \: n$ |
Zéro simple |
$1+j\omega r$ |
$20$ |
$0\: for\: \omega < \frac{1}{r}$ $20\: \log \omega r\: for \: \omega > \frac{1}{r}$ |
$0 \: for \: \omega < \frac{1}{r}$ $90 \: for \: \omega > \frac{1}{r}$ |
Poteau simple |
$\frac{1}{1+j\omega r}$ |
$-20$ |
$0\: for\: \omega < \frac{1}{r}$ $-20\: \log \omega r\: for\: \omega > \frac{1}{r}$ |
$0 \: for \: \omega < \frac{1}{r}$ $-90\: or \: 270 \: for\: \omega > \frac{1}{r}$ |
Terme dérivé du second ordre |
$\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )$ |
$40$ |
$40\: \log\: \omega_n\: for \: \omega < \omega_n$ $20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $40 \: \log \: \omega\:for \:\omega > \omega_n$ |
$0 \: for \: \omega < \omega_n$ $90 \: for \: \omega = \omega_n$ $180 \: for \: \omega > \omega_n$ |
Terme intégral du second ordre |
$\frac{1}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$ |
$-40$ |
$-40\: \log\: \omega_n\: for \: \omega < \omega_n$ $-20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $-40 \: \log \: \omega\:for \:\omega > \omega_n$ |
$-0 \: for \: \omega < \omega_n$ $-90 \: for \: \omega = \omega_n$ $-180 \: for \: \omega > \omega_n$ |
Considérez la fonction de transfert en boucle ouverte $G(s)H(s) = K$.
Ordre de grandeur $M = 20\: \log K$ dB
Angle de phase $\phi = 0$ degrés
Si $K = 1$, alors la magnitude est de 0 dB.
Si $K > 1$, alors la magnitude sera positive.
Si $K < 1$, alors la magnitude sera négative.
La figure suivante montre le tracé de Bode correspondant.


Le tracé de magnitude est une ligne horizontale, indépendante de la fréquence. La ligne 0 dB elle-même est le tracé de magnitude lorsque la valeur de K est un. Pour les valeurs positives de K, la ligne horizontale se décale$20 \:\log K$dB au-dessus de la ligne 0 dB. Pour les valeurs négatives de K, la ligne horizontale se décale$20\: \log K$dB en dessous de la ligne 0 dB. La ligne zéro degré elle-même est le tracé de phase pour toutes les valeurs positives de K.
Considérez la fonction de transfert en boucle ouverte $G(s)H(s) = s$.
Ordre de grandeur $M = 20 \log \omega$ dB
Angle de phase $\phi = 90^0$
À $\omega = 0.1$ rad / sec, la magnitude est de -20 dB.
À $\omega = 1$ rad / sec, la magnitude est de 0 dB.
À $\omega = 10$ rad / sec, la magnitude est de 20 dB.
La figure suivante montre le tracé de Bode correspondant.


Le graphique de magnitude est une ligne qui a une pente de 20 dB / déc. Cette ligne a commencé à$\omega = 0.1$rad / sec ayant une magnitude de -20 dB et il continue sur la même pente. Il touche la ligne 0 dB à$\omega = 1$rad / sec. Dans ce cas, le tracé de phase est de 90 0 ligne.
Considérez la fonction de transfert en boucle ouverte $G(s)H(s) = 1 + s\tau$.
Ordre de grandeur $M = 20\: log \sqrt{1 + \omega^2\tau^2}$ dB
Angle de phase $\phi = \tan^{-1}\omega\tau$ degrés
Pour $ω < \frac{1}{\tau}$ , la magnitude est de 0 dB et l'angle de phase est de 0 degré.
Pour $\omega > \frac{1}{\tau}$ , la magnitude est $20\: \log \omega\tau$dB et l'angle de phase est de 90 0 .
La figure suivante montre le tracé de Bode correspondant.

Le tracé de magnitude a une magnitude de 0 dB jusqu'à $\omega=\frac{1}{\tau}$rad / sec. De$\omega = \frac{1}{\tau}$rad / sec, il a une pente de 20 dB / déc. Dans ce cas, le tracé de phase a un angle de phase de 0 degré jusqu'à$\omega = \frac{1}{\tau}$rad / sec et à partir d'ici, il a un angle de phase de 90 0 . Ce graphique de Bode est appelé leasymptotic Bode plot.
Comme les tracés de magnitude et de phase sont représentés par des lignes droites, les tracés de Bode Exact ressemblent aux tracés de Bode asymptotiques. La seule différence est que les tracés Exact Bode auront des courbes simples au lieu de lignes droites.
De même, vous pouvez dessiner les tracés de Bode pour d'autres termes de la fonction de transfert en boucle ouverte qui sont donnés dans le tableau.
Dans ce chapitre, expliquons en détail comment construire (dessiner) des graphiques de Bode.
Règles de construction des tracés de Bode
Suivez ces règles lors de la construction d'un tracé de Bode.
Représente la fonction de transfert en boucle ouverte sous la forme de constante de temps standard.
Remplacer, $s=j\omega$ dans l'équation ci-dessus.
Trouvez les fréquences de coin et organisez-les par ordre croissant.
Considérez la fréquence de départ du tracé de Bode comme 1/10 ème de la fréquence de coin minimale ou 0,1 rad / s selon la valeur la plus petite et dessinez le tracé de Bode jusqu'à 10 fois la fréquence de coin maximale.
Dessinez les graphiques de magnitude pour chaque terme et combinez correctement ces graphiques.
Dessinez les graphiques de phase pour chaque terme et combinez correctement ces graphiques.
Note - La fréquence de coin est la fréquence à laquelle il y a un changement dans la pente du tracé de magnitude.
Exemple
Considérez la fonction de transfert en boucle ouverte d'un système de contrôle en boucle fermée
$$G(s)H(s)=\frac{10s}{(s+2)(s+5)}$$
Convertissons cette fonction de transfert en boucle ouverte en forme de constante de temps standard.
$$G(s)H(s)=\frac{10s}{2\left( \frac{s}{2}+1 \right )5 \left( \frac{s}{5}+1 \right )}$$
$$\Rightarrow G(s)H(s)=\frac{s}{\left( 1+\frac{s}{2} \right )\left( 1+\frac{s}{5} \right )}$$
Ainsi, nous pouvons dessiner le tracé de Bode dans une feuille semi-journal en utilisant les règles mentionnées précédemment.
Analyse de stabilité à l'aide de graphiques de Bode
À partir des graphiques de Bode, nous pouvons dire si le système de contrôle est stable, marginalement stable ou instable en fonction des valeurs de ces paramètres.
- Fréquence croisée de gain et fréquence croisée de phase
- Marge de gain et marge de phase
Fréquence de croisement de phase
La fréquence à laquelle le tracé de phase a la phase de -180 0 est appeléephase cross over frequency. Il est désigné par$\omega_{pc}$. L'unité de fréquence de coupure de phase estrad/sec.
Gain de fréquence de croisement
La fréquence à laquelle le tracé de magnitude a une magnitude de zéro dB est appelée gain cross over frequency. Il est désigné par$\omega_{gc}$. L'unité de la fréquence de croisement de gain estrad/sec.
La stabilité du système de commande basée sur la relation entre la fréquence de croisement de phase et la fréquence de croisement de gain est indiquée ci-dessous.
Si la phase passe sur la fréquence $\omega_{pc}$ est supérieure à la fréquence de croisement du gain $\omega_{gc}$, alors le système de contrôle est stable.
Si la phase passe sur la fréquence $\omega_{pc}$ est égal à la fréquence de croisement du gain $\omega_{gc}$, alors le système de contrôle est marginally stable.
Si la phase passe sur la fréquence $\omega_{pc}$ est inférieur à la fréquence de croisement du gain $\omega_{gc}$, alors le système de contrôle est unstable.
Gagner de la marge
Marge de gain $GM$ est égal au négatif de l'amplitude en dB à la fréquence de coupure de phase.
$$GM=20\log\left( \frac{1}{M_{pc}}\right )=20logM_{pc}$$
Où, $M_{pc}$est l'amplitude à la fréquence de coupure de phase. L'unité de marge de gain (GM) estdB.
Marge de phase
La formule de la marge de phase $PM$ est
$$PM=180^0+\phi_{gc}$$
Où, $\phi_{gc}$est l'angle de phase à la fréquence de croisement du gain. L'unité de marge de phase estdegrees.
La stabilité du système de contrôle basée sur la relation entre la marge de gain et la marge de phase est indiquée ci-dessous.
Si les deux la marge de gain $GM$ et la marge de phase $PM$ sont positifs, alors le système de contrôle est stable.
Si les deux la marge de gain $GM$ et la marge de phase $PM$ sont égaux à zéro, alors le système de contrôle est marginally stable.
Si la marge de gain $GM$ et / ou la marge de phase $PM$ sont / sont négatifs, alors le système de contrôle est unstable.
Dans les chapitres précédents, nous avons discuté des graphiques de Bode. Là, nous avons deux graphiques séparés pour la magnitude et la phase en fonction de la fréquence. Parlons maintenant des parcelles polaires. Le graphique polaire est un graphique qui peut être tracé entre la magnitude et la phase. Ici, les grandeurs sont représentées par des valeurs normales uniquement.
La forme polaire de $G(j\omega)H(j\omega)$ est
$$G(j\omega)H(j\omega)=|G(j\omega)H(j\omega)| \angle G(j\omega)H(j\omega)$$
le Polar plot est un tracé, qui peut être tracé entre la magnitude et l'angle de phase de $G(j\omega)H(j\omega)$ en variant $\omega$de zéro à ∞. La feuille de graphique polaire est illustrée dans la figure suivante.

Cette feuille graphique se compose de cercles concentriques et de lignes radiales. leconcentric circles et le radial linesreprésentent respectivement les amplitudes et les angles de phase. Ces angles sont représentés par des valeurs positives dans le sens anti-horaire. De même, nous pouvons représenter des angles avec des valeurs négatives dans le sens des aiguilles d'une montre. Par exemple, l'angle 270 0 dans le sens anti-horaire est égal à l'angle -90 0 dans le sens horaire.
Règles de dessin de tracés polaires
Suivez ces règles pour tracer les graphiques polaires.
Remplacer, $s = j\omega$ dans la fonction de transfert en boucle ouverte.
Écrivez les expressions pour la grandeur et la phase de $G(j\omega)H(j\omega)$.
Trouvez la magnitude de départ et la phase de $G(j\omega)H(j\omega)$ en substituant $\omega = 0$. Ainsi, le tracé polaire commence par cette magnitude et l'angle de phase.
Trouvez la magnitude finale et la phase de $G(j\omega)H(j\omega)$ en substituant $\omega = \infty$. Ainsi, le tracé polaire se termine par cette magnitude et l'angle de phase.
Vérifiez si le tracé polaire coupe l'axe réel, en faisant le terme imaginaire de $G(j\omega)H(j\omega)$ égal à zéro et trouvez la ou les valeurs de $\omega$.
Vérifiez si le tracé polaire coupe l'axe imaginaire, en faisant le terme réel de $G(j\omega)H(j\omega)$ égal à zéro et trouvez la ou les valeurs de $\omega$.
Pour dessiner plus clairement le graphique polaire, trouvez la magnitude et la phase de $G(j\omega)H(j\omega)$ en considérant la ou les autres valeurs de $\omega$.
Exemple
Considérez la fonction de transfert en boucle ouverte d'un système de contrôle en boucle fermée.
$$G(s)H(s)=\frac{5}{s(s+1)(s+2)}$$
Trouvons le graphique polaire de ce système de contrôle en utilisant les règles ci-dessus.
Step 1 - Suppléant, $s = j\omega$ dans la fonction de transfert en boucle ouverte.
$$G(j\omega)H(j\omega)=\frac{5}{j\omega(j\omega+1)(j\omega+2)}$$
L'ampleur de la fonction de transfert en boucle ouverte est
$$M=\frac{5}{\omega(\sqrt{\omega^2+1})(\sqrt{\omega^2+4})}$$
L'angle de phase de la fonction de transfert en boucle ouverte est
$$\phi=-90^0-\tan^{-1}\omega-\tan^{-1}\frac{\omega}{2}$$
Step 2 - Le tableau suivant montre l'amplitude et l'angle de phase de la fonction de transfert en boucle ouverte à $\omega = 0$ rad / sec et $\omega = \infty$ rad / sec.
| Fréquence (rad / sec) | Ordre de grandeur | Angle de phase (degrés) |
|---|---|---|
| 0 | ∞ | -90 ou 270 |
| ∞ | 0 | -270 ou 90 |
Ainsi, le tracé polaire commence à (∞, −90 0 ) et se termine à (0, −270 0 ). Les premier et second termes entre crochets indiquent respectivement l'amplitude et l'angle de phase.
Step 3- Sur la base des coordonnées polaires de début et de fin, ce tracé polaire coupera l'axe réel négatif. L'angle de phase correspondant à l'axe réel négatif est de -180 0 ou 180 0 . Ainsi, en assimilant l'angle de phase de la fonction de transfert en boucle ouverte à −180 0 ou 180 0 , nous obtiendrons le$\omega$ value as $\sqrt{2}$.
By substituting $\omega = \sqrt{2}$ in the magnitude of the open loop transfer function, we will get $M = 0.83$. Therefore, the polar plot intersects the negative real axis when $\omega = \sqrt{2}$ and the polar coordinate is (0.83,−1800).
So, we can draw the polar plot with the above information on the polar graph sheet.
Nyquist plots are the continuation of polar plots for finding the stability of the closed loop control systems by varying ω from −∞ to ∞. That means, Nyquist plots are used to draw the complete frequency response of the open loop transfer function.
Nyquist Stability Criterion
The Nyquist stability criterion works on the principle of argument. It states that if there are P poles and Z zeros are enclosed by the ‘s’ plane closed path, then the corresponding $G(s)H(s)$ plane must encircle the origin $P − Z$ times. So, we can write the number of encirclements N as,
$$N=P-Z$$
If the enclosed ‘s’ plane closed path contains only poles, then the direction of the encirclement in the $G(s)H(s)$ plane will be opposite to the direction of the enclosed closed path in the ‘s’ plane.
If the enclosed ‘s’ plane closed path contains only zeros, then the direction of the encirclement in the $G(s)H(s)$ plane will be in the same direction as that of the enclosed closed path in the ‘s’ plane.
Let us now apply the principle of argument to the entire right half of the ‘s’ plane by selecting it as a closed path. This selected path is called the Nyquist contour.
We know that the closed loop control system is stable if all the poles of the closed loop transfer function are in the left half of the ‘s’ plane. So, the poles of the closed loop transfer function are nothing but the roots of the characteristic equation. As the order of the characteristic equation increases, it is difficult to find the roots. So, let us correlate these roots of the characteristic equation as follows.
The Poles of the characteristic equation are same as that of the poles of the open loop transfer function.
The zeros of the characteristic equation are same as that of the poles of the closed loop transfer function.
We know that the open loop control system is stable if there is no open loop pole in the the right half of the ‘s’ plane.
i.e.,$P=0 \Rightarrow N=-Z$
We know that the closed loop control system is stable if there is no closed loop pole in the right half of the ‘s’ plane.
i.e.,$Z=0 \Rightarrow N=P$
Nyquist stability criterionindique que le nombre d'encerclements autour du point critique (1 + j0) doit être égal aux pôles de l'équation caractéristique, qui n'est rien d'autre que les pôles de la fonction de transfert en boucle ouverte dans la moitié droite du plan «s». Le décalage de l'origine vers (1 + j0) donne le plan d'équation caractéristique.
Règles de dessin des tracés de Nyquist
Suivez ces règles pour tracer les parcelles de Nyquist.
Localisez les pôles et les zéros de la fonction de transfert en boucle ouverte $G(s)H(s)$ dans le plan 's'.
Dessinez le graphique polaire en variant $\omega$de zéro à l'infini. Si pôle ou zéro présent à s = 0, alors varier$\omega$ de 0+ à l'infini pour dessiner un tracé polaire.
Dessinez l'image miroir du tracé polaire ci-dessus pour les valeurs de $\omega$allant de −∞ à zéro (0 - si un pôle ou un zéro est présent à s = 0).
Le nombre de demi-cercles de rayon infini sera égal au nombre de pôles ou de zéros à l'origine. Le demi-cercle de rayon infini commencera au point où l'image miroir du tracé polaire se termine. Et ce demi-cercle de rayon infini se terminera au point où le tracé polaire commence.
Après avoir tracé le graphique de Nyquist, nous pouvons trouver la stabilité du système de contrôle en boucle fermée en utilisant le critère de stabilité de Nyquist. Si le point critique (-1 + j0) se situe en dehors de l'encerclement, alors le système de contrôle en boucle fermée est absolument stable.
Analyse de stabilité à l'aide des graphiques de Nyquist
À partir des graphiques de Nyquist, nous pouvons identifier si le système de contrôle est stable, marginalement stable ou instable sur la base des valeurs de ces paramètres.
- Fréquence croisée de gain et fréquence croisée de phase
- Marge de gain et marge de phase
Fréquence de croisement de phase
La fréquence à laquelle le graphique de Nyquist coupe l'axe réel négatif (l'angle de phase est de 180 0 ) est connue sous le nom dephase cross over frequency. Il est désigné par$\omega_{pc}$.
Gain de fréquence de croisement
La fréquence à laquelle le graphique de Nyquist a la magnitude d'un est connue sous le nom de gain cross over frequency. Il est désigné par$\omega_{gc}$.
La stabilité du système de commande basée sur la relation entre la fréquence de croisement de phase et la fréquence de croisement de gain est indiquée ci-dessous.
Si la phase passe sur la fréquence $\omega_{pc}$ est supérieure à la fréquence de croisement du gain $\omega_{gc}$, alors le système de contrôle est stable.
Si la phase passe sur la fréquence $\omega_{pc}$ est égal à la fréquence de croisement du gain $\omega_{gc}$, alors le système de contrôle est marginally stable.
Si la fréquence de croisement de phase $\omega_{pc}$ est inférieur à la fréquence de croisement du gain $\omega_{gc}$, alors le système de contrôle est unstable.
Gagner de la marge
La marge de gain $GM$ est égal à l'inverse de l'amplitude du graphique de Nyquist à la fréquence de croisement de phase.
$$GM=\frac{1}{M_{pc}}$$
Où, $M_{pc}$ est la grandeur en échelle normale à la fréquence de croisement de phase.
Marge de phase
La marge de phase $PM$est égal à la somme de 180 0 et de l'angle de phase à la fréquence de croisement du gain.
$$PM=180^0+\phi_{gc}$$
Où, $\phi_{gc}$ est l'angle de phase à la fréquence de croisement du gain.
La stabilité du système de contrôle basée sur la relation entre la marge de gain et la marge de phase est indiquée ci-dessous.
Si la marge de gain $GM$ est supérieur à un et la marge de phase $PM$ est positif, alors le système de contrôle est stable.
Si la marge de gain $GM$ est égal à un et la marge de phase $PM$ est de zéro degré, alors le système de contrôle est marginally stable.
Si la marge de gain $GM$ est inférieur à un et / ou la marge de phase $PM$ est négatif, alors le système de contrôle est unstable.
Il existe trois types de compensateurs: les compensateurs de retard, d'avance et d'avance. Ceux-ci sont les plus couramment utilisés.
Compensateur de décalage
Le compensateur de décalage est un réseau électrique qui produit une sortie sinusoïdale ayant le décalage de phase lorsqu'une entrée sinusoïdale est appliquée. Le circuit compensateur de retard dans le domaine «s» est illustré dans la figure suivante.

Ici, le condensateur est en série avec la résistance $R_2$ et la sortie est mesurée à travers cette combinaison.
La fonction de transfert de ce compensateur de retard est -
$$\frac{V_o(s)}{V_i(s)}=\frac{1}{\alpha} \left( \frac{s+\frac{1}{\tau}}{s+\frac{1}{\alpha\tau}} \right )$$
Où,
$$\tau=R_2C$$
$$\alpha=\frac{R_1+R_2}{R_2}$$
À partir de l'équation ci-dessus, $\alpha$ est toujours supérieur à un.
À partir de la fonction de transfert, nous pouvons conclure que le compensateur de retard a un pôle à $s = − \frac{1}{\alpha \tau}$ et un zéro à $s = −\frac{1}{\tau}$. Cela signifie que le pôle sera plus proche de l'origine dans la configuration pôle-zéro du compensateur de retard.
Remplacer, $s = j\omega$ dans la fonction de transfert.
$$\frac{V_o(j\omega)}{V_i(j\omega)}=\frac{1}{\alpha}\left( \frac{j\omega+\frac{1}{\tau}}{j\omega+\frac{1}{\alpha\tau}}\right )$$
Angle de phase $\phi = \tan^{−1} \omega\tau − tan^{−1} \alpha\omega\tau$
On sait que la phase du signal sinusoïdal de sortie est égale à la somme des angles de phase du signal sinusoïdal d'entrée et de la fonction de transfert.
Ainsi, pour produire le décalage de phase à la sortie de ce compensateur, l'angle de phase de la fonction de transfert doit être négatif. Cela se produira quand$\alpha > 1$.
Compensateur principal
Le compensateur de plomb est un réseau électrique qui produit une sortie sinusoïdale ayant une avance de phase lorsqu'une entrée sinusoïdale est appliquée. Le circuit compensateur de plomb dans le domaine «s» est illustré dans la figure suivante.

Ici, le condensateur est parallèle à la résistance $R_1$ et la sortie est mesurée aux bornes de la résistance $ R_2.
La fonction de transfert de ce compensateur de plomb est -
$$ \ frac {V_o (s)} {V_i (s)} = \ beta \ left (\ frac {s \ tau + 1} {\ beta s \ tau + 1} \ right) $$
Où,
$$ \ tau = R_1C $$
$$ \ beta = \ frac {R_2} {R_1 + R_2} $$
À partir de la fonction de transfert, nous pouvons conclure que le compensateur de plomb a un pôle à $ s = - \ frac {1} {\ beta}$ and zero at $s = - \ frac {1} {\ beta \ tau} $.
Remplacez, $ s = j \ omega $ dans la fonction de transfert.
$$ \ frac {V_o (j \ omega)} {V_i (j \ omega)} = \ beta \ left (\ frac {j \ omega \ tau + 1} {\ beta j \ omega \ tau + 1} \ right ) $$
Angle de phase $ \ phi = tan ^ {- 1} \ omega \ tau - tan ^ {- 1} \ beta \ omega \ tau $
On sait que la phase du signal sinusoïdal de sortie est égale à la somme des angles de phase du signal sinusoïdal d'entrée et de la fonction de transfert.
Ainsi, afin de produire l'avance de phase à la sortie de ce compensateur, l'angle de phase de la fonction de transfert doit être positif. Cela se produira lorsque $ 0 <\ beta <1 $. Par conséquent, le zéro sera plus proche de l'origine dans la configuration pôle-zéro du compensateur de plomb.
Compensateur de retard
Le compensateur Lag-Lead est un réseau électrique qui produit un décalage de phase dans une région de fréquence et une avance de phase dans une autre région de fréquence. C'est une combinaison du retard et des compensateurs de plomb. Le circuit compensateur de retard dans le domaine «s» est illustré dans la figure suivante.

Ce circuit semble que les deux compensateurs sont en cascade. Ainsi, la fonction de transfert de ce circuit sera le produit des fonctions de transfert du conducteur et des compensateurs de retard.
$$ \ frac {V_o (s)} {V_i (s)} = \ beta \ left (\ frac {s \ tau_1 + 1} {\ beta s \ tau_1 + 1} \ right) \ frac {1} {\ alpha} \ left (\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right) $$
Nous savons que $ \ alpha \ beta = 1 $.
$$ \ Rightarrow \ frac {V_o (s)} {V_i (s)} = \ left (\ frac {s + \ frac {1} {\ tau_1}} {s + \ frac {1} {\ beta \ tau_1}} \ right) \ left (\ frac {s + \ frac {1} {\ tau_2}} {s + \ frac {1} {\ alpha \ tau_2}} \ right) $$
Où,
$$ \ tau_1 = R_1C_1 $$
$$ \ tau_2 = R_2C_2 $$
Les différents types de contrôleurs sont utilisés pour améliorer les performances des systèmes de contrôle. Dans ce chapitre, nous aborderons les contrôleurs de base tels que les contrôleurs proportionnel, dérivé et intégral.
Contrôleur proportionnel
Le régulateur proportionnel produit une sortie, qui est proportionnelle au signal d'erreur.
$$ u (t) \ propto e (t) $$
$$ \ Flèche droite u (t) = K_P e (t) $$
Appliquer la transformation de Laplace des deux côtés -
$$ U (s) = K_P E (s) $$
$$ \ frac {U (s)} {E (s)} = K_P $$
Par conséquent, la fonction de transfert du contrôleur proportionnel est $ K_P $.
Où,
U (s) est la transformée de Laplace du signal d'actionnement u (t)
E (s) est la transformée de Laplace du signal d'erreur e (t)
K P est la constante de proportionnalité
Le schéma de principe du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur proportionnel est illustré dans la figure suivante.

Le contrôleur proportionnel est utilisé pour modifier la réponse transitoire selon l'exigence.
Contrôleur dérivé
Le contrôleur dérivé produit une sortie, qui est dérivée du signal d'erreur.
$$ u (t) = K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$
Appliquez la transformation de Laplace des deux côtés.
$$ U (s) = K_D sE (s) $$
$$ \ frac {U (s)} {E (s)} = K_D s $$
Par conséquent, la fonction de transfert du contrôleur dérivé est $ K_D s $.
Où, $ K_D $ est la constante dérivée.
Le schéma de principe du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur dérivé est illustré dans la figure suivante.

Le contrôleur dérivé est utilisé pour transformer le système de contrôle instable en un système stable.
Contrôleur intégral
Le contrôleur intégral produit une sortie, qui est intégrale du signal d'erreur.
$$ u (t) = K_I \ int e (t) dt $$
Appliquer la transformation de Laplace des deux côtés -
$$ U (s) = \ frac {K_I E (s)} {s} $$
$$ \ frac {U (s)} {E (s)} = \ frac {K_I} {s} $$
Par conséquent, la fonction de transfert du contrôleur intégral est $ \ frac {K_I} {s} $.
Où, $ K_I $ est la constante intégrale.
Le schéma de principe du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur intégré est illustré dans la figure suivante.

Le contrôleur intégré est utilisé pour diminuer l'erreur en régime permanent.
Parlons maintenant de la combinaison de contrôleurs de base.
Contrôleur de dérivée proportionnelle (PD)
Le contrôleur proportionnel dérivé produit une sortie, qui est la combinaison des sorties des contrôleurs proportionnel et dérivé.
$$ u (t) = K_P e (t) + K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$
Appliquer la transformation de Laplace des deux côtés -
$$ U (s) = (K_P + K_D s) E (s) $$
$$ \ frac {U (s)} {E (s)} = K_P + K_D s $$
Par conséquent, la fonction de transfert du contrôleur de dérivée proportionnelle est $ K_P + K_D s $.
Le schéma de principe du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur de dérivation proportionnelle est illustré dans la figure suivante.

Le contrôleur de dérivation proportionnelle est utilisé pour améliorer la stabilité du système de contrôle sans affecter l'erreur en régime permanent.
Contrôleur proportionnel intégral (PI)
Le contrôleur proportionnel intégral produit une sortie, qui est la combinaison des sorties des contrôleurs proportionnel et intégral.
$$ u (t) = K_P e (t) + K_I \ int e (t) dt $$
Appliquer la transformation de Laplace des deux côtés -
$$ U (s) = \ gauche (K_P + \ frac {K_I} {s} \ droite) E (s) $$
$$ \ frac {U (s)} {E (s)} = K_P + \ frac {K_I} {s} $$
Par conséquent, la fonction de transfert du contrôleur proportionnel intégral est $ K_P + \ frac {K_I} {s} $.
Le schéma de principe du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur proportionnel intégral est illustré dans la figure suivante.

Le contrôleur intégral proportionnel est utilisé pour diminuer l'erreur en régime permanent sans affecter la stabilité du système de commande.
Contrôleur PID (Proportional Integral Derivative)
Le contrôleur dérivé intégral proportionnel produit une sortie, qui est la combinaison des sorties des contrôleurs proportionnel, intégral et dérivé.
$$ u (t) = K_P e (t) + K_I \ int e (t) dt + K_D \ frac {\ text {d} e (t)} {\ text {d} t} $$
Appliquer la transformation de Laplace des deux côtés -
$$ U (s) = \ gauche (K_P + \ frac {K_I} {s} + K_D s \ droite) E (s) $$
$$ \ frac {U (s)} {E (s)} = K_P + \ frac {K_I} {s} + K_D s $$
Par conséquent, la fonction de transfert du contrôleur de dérivée intégrale proportionnelle est $ K_P + \ frac {K_I} {s} + K_D s $.
Le schéma de principe du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur de dérivation intégrale proportionnelle est illustré dans la figure suivante.

Le contrôleur de dérivée intégrale proportionnelle est utilisé pour améliorer la stabilité du système de commande et pour diminuer l'erreur en régime permanent.
le state space model du système LTI (Linear Time-Invariant) peut être représenté comme suit:
$$ \ dot {X} = AX + BU $$
$$ Y = CX + DU $$
Les première et deuxième équations sont respectivement appelées équation d'état et équation de sortie.
Où,
X et $ \ dot {X} $ sont respectivement le vecteur d'état et le vecteur d'état différentiel.
U et Y sont respectivement le vecteur d'entrée et le vecteur de sortie.
A est la matrice du système.
B et C sont les matrices d'entrée et de sortie.
D est la matrice d'avance.
Concepts de base du modèle d'espace d'état
La terminologie de base suivante impliquée dans ce chapitre.
Etat
Il s'agit d'un groupe de variables, qui résume l'historique du système afin de prédire les valeurs futures (sorties).
État variable
Le nombre de variables d'état requises est égal au nombre d'éléments de stockage présents dans le système.
Examples - courant traversant l'inductance, tension aux bornes du condensateur
Vecteur d'état
C'est un vecteur qui contient les variables d'état sous forme d'éléments.
Dans les chapitres précédents, nous avons discuté de deux modèles mathématiques des systèmes de contrôle. Ce sont le modèle d'équation différentielle et le modèle de fonction de transfert. Le modèle d'espace d'états peut être obtenu à partir de n'importe lequel de ces deux modèles mathématiques. Parlons maintenant de ces deux méthodes une par une.
Modèle d'espace d'état à partir d'une équation différentielle
Considérez la série suivante du circuit RLC. Il a une tension d'entrée, $ v_i (t)$ and the current flowing through the circuit is $i (t) $.

Il y a deux éléments de stockage (inductance et condensateur) dans ce circuit. Ainsi, le nombre de variables d'état est égal à deux et ces variables d'état sont le courant circulant dans l'inductance, $ i (t)$ and the voltage across capacitor, $v_c (t) $.
À partir du circuit, la tension de sortie, $ v_0 (t)$ is equal to the voltage across capacitor, $v_c (t) $.
$$ v_0 (t) = v_c (t) $$
Appliquez KVL autour de la boucle.
$$ v_i (t) = Ri (t) + L \ frac {\ text {d} i (t)} {\ text {d} t} + v_c (t) $$
$$ \ Rightarrow \ frac {\ text {d} i (t)} {\ text {d} t} = - \ frac {Ri (t)} {L} - \ frac {v_c (t)} {L} + \ frac {v_i (t)} {L} $$
La tension aux bornes du condensateur est -
$$ v_c (t) = \ frac {1} {C} \ int i (t) dt $$
Différenciez l'équation ci-dessus par rapport au temps.
$$ \ frac {\ text {d} v_c (t)} {\ text {d} t} = \ frac {i (t)} {C} $$
Vecteur d'état, $ X = \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} $
Vecteur d'état différentiel, $ \ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t )} {\ text {d} t} \ end {bmatrix} $
Nous pouvons organiser les équations différentielles et l'équation de sortie dans la forme standard du modèle d'espace d'état comme,
$$ \ dot {X} = \ begin {bmatrix} \ frac {\ text {d} i (t)} {\ text {d} t} \\\ frac {\ text {d} v_c (t)} { \ text {d} t} \ end {bmatrix} = \ begin {bmatrix} - \ frac {R} {L} & - \ frac {1} {L} \\\ frac {1} {C} & 0 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} + \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix} \ begin {bmatrix } v_i (t) \ end {bmatrix} $$
$$ Y = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} i (t) \\ v_c (t) \ end {bmatrix} $$
Où,
$$ A = \ begin {bmatrix} - \ frac {R} {L} & - \ frac {1} {L} \\\ frac {1} {C} & 0 \ end {bmatrix}, \: B = \ begin {bmatrix} \ frac {1} {L} \\ 0 \ end {bmatrix}, \: C = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \: et \: D = \ begin {bmatrix } 0 \ end {bmatrix} $$
Modèle d'espace d'état de la fonction de transfert
Considérez les deux types de fonctions de transfert en fonction du type de termes présents dans le numérateur.
- Fonction de transfert ayant un terme constant dans le numérateur.
- Fonction de transfert ayant une fonction polynomiale de «s» dans le numérateur.
Fonction de transfert ayant un terme constant dans le numérateur
Considérez la fonction de transfert suivante d'un système
$$ \ frac {Y (s)} {U (s)} = \ frac {b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1s + a_0} $ $
Réorganisez, l'équation ci-dessus comme
$$ (s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0) Y (s) = b_0 U (s) $$
Appliquez la transformée de Laplace inverse des deux côtés.
$$ \ frac {\ text {d} ^ ny (t)} {\ text {d} t ^ n} + a_ {n-1} \ frac {\ text {d} ^ {n-1} y (t )} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} y (t)} {\ text {d} t} + a_0y (t) = b_0 u (t) $$
Laisser
$$ y (t) = x_1 $$
$$ \ frac {\ text {d} y (t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$
$$ \ frac {\ text {d} ^ 2y (t)} {\ text {d} t ^ 2} = x_3 = \ dot {x} _2 $$
$$. $$
$$. $$
$$. $$
$$ \ frac {\ text {d} ^ {n-1} y (t)} {\ text {d} t ^ {n-1}} = x_n = \ dot {x} _ {n-1} $ $
$$ \ frac {\ text {d} ^ ny (t)} {\ text {d} t ^ n} = \ dot {x} _n $$
et $ u (t) = u $
Ensuite,
$$ \ dot {x} _n + a_ {n-1} x_n + ... + a_1x_2 + a_0x_1 = b_0 u $$
À partir de l'équation ci-dessus, nous pouvons écrire l'équation d'état suivante.
$$ \ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + b_0 u $$
L'équation de sortie est -
$$ y (t) = y = x_1 $$
Le modèle d'espace d'états est -
$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ point {x} _n \ end {bmatrix} $
$$ = \ begin {bmatrix} 0 & 1 & 0 & \ dotso & 0 & 0 \\ 0 & 0 & 1 & \ dotso & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ dotso & \ vdots & \ vdots \\ 0 & 0 & 0 & \ dotso & 0 & 1 \\ - a_0 & -a_1 & -a_2 & \ dotso & -a_ {n-2} & -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix} $$
$$ Y = \ begin {bmatrix} 1 & 0 & \ dotso & 0 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} $$
Ici, $ D = \ left [0 \ right]. $
Exemple
Trouvez le modèle d'espace d'états pour le système ayant une fonction de transfert.
$$ \ frac {Y (s)} {U (s)} = \ frac {1} {s ^ 2 + s + 1} $$
Réorganisez, l'équation ci-dessus comme,
$$ (s ^ 2 + s + 1) Y (s) = U (s) $$
Appliquez la transformée de Laplace inverse des deux côtés.
$$ \ frac {\ text {d} ^ 2y (t)} {\ text {d} t ^ 2} + \ frac {\ text {d} y (t)} {\ text {d} t} + y (t) = u (t) $$
Laisser
$$ y (t) = x_1 $$
$$ \ frac {\ text {d} y (t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$
et $ u (t) = u $
Ensuite, l'équation d'état est
$$ \ dot {x} _2 = -x_1-x_2 + u $$
L'équation de sortie est
$$ y (t) = y = x_1 $$
Le modèle d'espace d'états est
$$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} 0 & 1 \\ - 1 & -1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} \ left [u \ right] $$
$$ Y = \ begin {bmatrix} 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$
Fonction de transfert ayant une fonction polynomiale de 's' dans le numérateur
Considérez la fonction de transfert suivante d'un système
$$ \ frac {Y (s)} {U (s)} = \ frac {b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} $$
$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ left (\ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} \ droite) (b_n s ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0) $$
L'équation ci-dessus se présente sous la forme d'un produit de fonctions de transfert de deux blocs, qui sont en cascade.
$$ \ frac {Y (s)} {U (s)} = \ left (\ frac {V (s)} {U (s)} \ right) \ left (\ frac {Y (s)} {V (s)} \ droite) $$
Ici,
$$ \ frac {V (s)} {U (s)} = \ frac {1} {s ^ n + a_ {n-1} s ^ {n-1} + ... + a_1 s + a_0} $$
Réorganisez, l'équation ci-dessus comme
$$ (s ^ n + a_ {n-1} s ^ {n-1} + ... + a_0) V (s) = U (s) $$
Appliquez la transformée de Laplace inverse des deux côtés.
$$ \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} + a_ {n-1} \ frac {\ text {d} ^ {n-1} v (t )} {\ text {d} t ^ {n-1}} + ... + a_1 \ frac {\ text {d} v (t)} {\ text {d} t} + a_0v (t) = u (t) $$
Laisser
$$ v (t) = x_1 $$
$$ \ frac {\ text {d} v ((t)} {\ text {d} t} = x_2 = \ dot {x} _1 $$
$$ \ frac {\ text {d} ^ 2v (t)} {\ text {d} t ^ 2} = x_3 = \ dot {x} _2 $$
$$. $$
$$. $$
$$. $$
$$ \ frac {\ text {d} ^ {n-1} v (t)} {\ text {d} t ^ {n-1}} = x_n = \ dot {x} _ {n-1} $ $
$$ \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} = \ dot {x} _n $$
et $ u (t) = u $
Ensuite, l'équation d'état est
$$ \ dot {x} _n = -a_0x_1-a_1x_2 -...- a_ {n-1} x_n + u $$
Considérer,
$$ \ frac {Y (s)} {V (s)} = b_ns ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0 $$
Réorganisez, l'équation ci-dessus comme
$$ Y (s) = (b_ns ^ n + b_ {n-1} s ^ {n-1} + ... + b_1s + b_0) V (s) $$
Appliquez la transformée de Laplace inverse des deux côtés.
$$ y (t) = b_n \ frac {\ text {d} ^ nv (t)} {\ text {d} t ^ n} + b_ {n-1} \ frac {\ text {d} ^ {n -1} v (t)} {\ text {d} t ^ {n-1}} + ... + b_1 \ frac {\ text {d} v (t)} {\ text {d} t} + b_0v (t) $$
En remplaçant les variables d'état et $ y (t) = y $ dans l'équation ci-dessus, obtiendra l'équation de sortie comme,
$$ y = b_n \ dot {x} _n + b_ {n-1} x_n + ... + b_1x_2 + b_0x_1 $$
Remplacez, $ \ dot {x} _n $ valeur dans l'équation ci-dessus.
$$ y = b_n (-a_0x_1-a_1x_2 -...- a_ {n-1} x_n + u) + b_ {n-1} x_n + ... + b_1x_2 + b_0x_1 $$
$$ y = (b_0-b_na_0) x_1 + (b_1-b_na_1) x_2 + ... + (b_ {n-1} -b_na_ {n-1}) x_n + b_n u $$
Le modèle d'espace d'états est
$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \\\ vdots \\\ dot {x} _ {n-1} \\\ point {x} _n \ end {bmatrix} $
$$ = \ begin {bmatrix} 0 & 1 & 0 & \ dotso & 0 & 0 \\ 0 & 0 & 1 & \ dotso & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ dotso & \ vdots & \ vdots \\ 0 & 0 & 0 & \ dotso & 0 & 1 \\ - a_0 & -a_1 & -a_2 & \ dotso & -a_ {n-2} & -a_ {n-1} \ end {bmatrix } \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} + \ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ b_0 \ end {bmatrix} \ begin {bmatrix} u \ end {bmatrix} $$
$$ Y = [b_0-b_na_0 \ quad b_1-b_na_1 \ quad ... \ quad b_ {n-2} -b_na_ {n-2} \ quad b_ {n-1} -b_na_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n-1} \\ x_n \ end {bmatrix} $$
Si $ b_n = 0 $, alors,
$$ Y = [b_0 \ quad b_1 \ quad ... \ quad b_ {n-2} \ quad b_ {n-1}] \ begin {bmatrix} x_1 \\ x_2 \\\ vdots \\ x_ {n- 1} \\ x_n \ end {bmatrix} $$
Dans le chapitre précédent, nous avons appris comment obtenir le modèle d'espace d'états à partir d'une équation différentielle et d'une fonction de transfert. Dans ce chapitre, discutons de la façon d'obtenir une fonction de transfert à partir du modèle d'espace d'état.
Fonction de transfert à partir du modèle d'espace d'état
Nous savons que le modèle d'espace d'état d'un système LTI (Linear Time-Invariant) est -
$$ \ dot {X} = AX + BU $$
$$ Y = CX + DU $$
Appliquez la transformation de Laplace des deux côtés de l'équation d'état.
$$ sX (s) = AX (s) + BU (s) $$
$$ \ Flèche droite (sI-A) X (s) = BU (s) $$
$$ \ Rightarrow X (s) = (sI-A) ^ {- 1} BU (s) $$
Appliquez la transformation de Laplace des deux côtés de l'équation de sortie.
$$ Y (s) = CX (s) + DU (s) $$
Remplacez la valeur X (s) dans l'équation ci-dessus.
$$ \ Rightarrow Y (s) = C (sI-A) ^ {- 1} BU (s) + DU (s) $$
$$ \ Flèche droite Y (s) = [C (sI-A) ^ {- 1} B + D] U (s) $$
$$ \ Rightarrow \ frac {Y (s)} {U (s)} = C (sI-A) ^ {- 1} B + D $$
L'équation ci-dessus représente la fonction de transfert du système. Ainsi, nous pouvons calculer la fonction de transfert du système en utilisant cette formule pour le système représenté dans le modèle d'espace d'états.
Note - Lorsque $ D = [0] $, la fonction de transfert sera
$$ \ frac {Y (s)} {U (s)} = C (sI-A) ^ {- 1} B $$
Example
Calculons la fonction de transfert du système représenté dans le modèle d'espace d'états comme,
$$ \ dot {X} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u] $$
$$ Y = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$
Ici,
$$ A = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix}, \ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}, \ quad C = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ quad et \ quad D = [0] $$
La formule de la fonction de transfert lorsque $ D = [0] $ est -
$$ \ frac {Y (s)} {U (s)} = C (sI-A) ^ {- 1} B $$
Remplacez les matrices A, B et C dans l'équation ci-dessus.
$$ \ frac {Y (s)} {U (s)} = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} s + 1 & 1 \\ - 1 & s \ end {bmatrix } ^ {- 1} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$
$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ frac {\ begin {bmatrix} s & -1 \\ 1 & s + 1 \ end {bmatrix}} {(s + 1) s-1 (-1)} \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$
$$ \ Rightarrow \ frac {Y (s)} {U (s)} = \ frac {\ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} s \\ 1 \ end {bmatrix}} {s ^ 2 + s + 1} = \ frac {1} {s ^ 2 + s + 1} $$
Par conséquent, la fonction de transfert du système pour le modèle d'espace d'états donné est
$$ \ frac {Y (s)} {U (s)} = \ frac {1} {s ^ 2 + s + 1} $$
Matrice de transition d'état et ses propriétés
Si le système a des conditions initiales, alors il produira une sortie. Puisque cette sortie est présente même en l'absence d'entrée, elle est appeléezero input response$ x_ {ZIR} (t) $. Mathématiquement, nous pouvons l'écrire comme,
$$ x_ {ZIR} (t) = e ^ {At} X (0) = L ^ {- 1} \ left \ {\ left [sI-A \ right] ^ {- 1} X (0) \ right \} $$
À partir de la relation ci-dessus, nous pouvons écrire la matrice de transition d'état $ \ phi (t) $ comme
$$ \ phi (t) = e ^ {At} = L ^ {- 1} [sI-A] ^ {- 1} $$
Ainsi, la réponse d'entrée nulle peut être obtenue en multipliant la matrice de transition d'état $ \ phi (t) $ avec la matrice des conditions initiales.
Voici les propriétés de la matrice de transition d'état.
Si $ t = 0 $, alors la matrice de transition d'état sera égale à une matrice d'identité.
$$ \ phi (0) = I $$
L'inverse de la matrice de transition d'état sera le même que celui de la matrice de transition d'état simplement en remplaçant «t» par «-t».
$$ \ phi ^ {- 1} (t) = \ phi (−t) $$
Si $ t = t_1 + t_2$ , then the corresponding state transition matrix is equal to the multiplication of the two state transition matrices at $t = t_1$ and $t = t_2 $.
$$ \ phi (t_1 + t_2) = \ phi (t_1) \ phi (t_2) $$
Contrôlabilité et observabilité
Parlons maintenant de la contrôlabilité et de l'observabilité du système de contrôle un par un.
Contrôlabilité
On dit qu'un système de contrôle est controllable si les états initiaux du système de commande sont transférés (modifiés) vers certains autres états souhaités par une entrée commandée en durée finie.
Nous pouvons vérifier la contrôlabilité d'un système de contrôle en utilisant Kalman’s test.
Écrivez la matrice $ Q_c $ sous la forme suivante.
$$ Q_c = \ gauche [B \ quad AB \ quad A ^ 2B \ quad ... \ quad A ^ {n-1} B \ droite] $$
Trouvez le déterminant de la matrice $ Q_c $ et s'il n'est pas égal à zéro, alors le système de contrôle est contrôlable.
Observabilité
On dit qu'un système de contrôle est observable s'il est capable de déterminer les états initiaux du système de contrôle en observant les sorties en durée finie.
Nous pouvons vérifier l'observabilité d'un système de contrôle en utilisant Kalman’s test.
Écrivez la matrice $ Q_o $ sous la forme suivante.
$$ Q_o = \ gauche [C ^ T \ quad A ^ TC ^ T \ quad (A ^ T) ^ 2C ^ T \ quad ... \ quad (A ^ T) ^ {n-1} C ^ T \ droite] $$
Trouvez le déterminant de la matrice $ Q_o $ et s'il n'est pas égal à zéro, alors le système de contrôle est observable.
Example
Vérifions la contrôlabilité et l'observabilité d'un système de contrôle qui est représenté dans le modèle d'espace d'états comme,
$$ \ dot {x} = \ begin {bmatrix} \ dot {x} _1 \\\ dot {x} _2 \ end {bmatrix} = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} + \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} [u] $$
$$ Y = \ begin {bmatrix} 0 & 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ x_2 \ end {bmatrix} $$
Ici,
$$ A = \ begin {bmatrix} -1 & -1 \\ 1 & 0 \ end {bmatrix}, \ quad B = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}, \ quad \ begin {bmatrix } 0 & 1 \ end {bmatrix}, D = [0] \ quad et \ quad n = 2 $$
Pour $ n = 2$, the matrix $Q_c $ sera
$$ Q_c = \ gauche [B \ quad AB \ droite] $$
Nous obtiendrons le produit des matrices A et B comme,
$$ AB = \ begin {bmatrix} -1 \\ 1 \ end {bmatrix} $$
$$ \ Rightarrow Q_c = \ begin {bmatrix} 1 & -1 \\ 0 & 1 \ end {bmatrix} $$
$$ | Q_c | = 1 \ neq 0 $$
Puisque le déterminant de la matrice $ Q_c $ n'est pas égal à zéro, le système de contrôle donné est contrôlable.
Pour $ n = 2$, the matrix $Q_o $ sera -
$$ Q_o = \ gauche [C ^ T \ quad A ^ TC ^ T \ droite] $$
Ici,
$$ A ^ T = \ begin {bmatrix} -1 & 1 \\ - 1 & 0 \ end {bmatrix} \ quad et \ quad C ^ T = \ begin {bmatrix} 0 \\ 1 \ end {bmatrix} $ $
On obtiendra le produit des matrices $ A ^ T$ and $C ^ T $ comme
$$ A ^ TC ^ T = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix} $$
$$ \ Rightarrow Q_o = \ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix} $$
$$ \ Flèche droite | Q_o | = -1 \ quad \ neq 0 $$
Puisque, le déterminant de la matrice $ Q_o $ n'est pas égal à zéro, le système de contrôle donné est observable.
Par conséquent, le système de contrôle donné est à la fois contrôlable et observable.