Analogies électriques des systèmes mécaniques
On dit que deux systèmes sont analogous l'un à l'autre si les deux conditions suivantes sont remplies.
- Les deux systèmes sont physiquement différents
- La modélisation d'équations différentielles de ces deux systèmes est la même
Les systèmes électriques et les systèmes mécaniques sont deux systèmes physiquement différents. Il existe deux types d'analogies électriques des systèmes mécaniques de translation. Ce sont l'analogie de la tension de force et l'analogie du courant de force.
Analogie de tension de force
Dans l'analogie de la tension de force, les équations mathématiques de translational mechanical system sont comparées aux équations de maillage du système électrique.
Considérez le système mécanique de translation suivant, comme illustré dans la figure suivante.
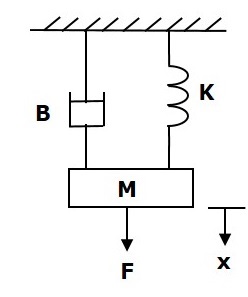
le force balanced equation car ce système est
$$ F = F_m + F_b + F_k $$
$ \ Rightarrow F = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} + B \ frac {\ text {d} x} {\ text {d} t} + Kx $ (Equation 1)
Tenez compte du système électrique suivant, comme illustré dans la figure suivante. Ce circuit se compose d'une résistance, d'une inductance et d'un condensateur. Tous ces éléments électriques sont connectés en série. La tension d'entrée appliquée à ce circuit est de $ V $ volts et le courant traversant le circuit est de $ i $ ampères.

L'équation de maillage pour ce circuit est
$ V = Ri + L \ frac {\ text {d} i} {\ text {d} t} + \ frac {1} {c} \ int idt $ (Equation 2)
Remplacez, $ i = \ frac {\ text {d} q} {\ text {d} t} $ dans l'équation 2.
$$ V = R \ frac {\ text {d} q} {\ text {d} t} + L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + \ frac { q} {C} $$
$ \ Rightarrow V = L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + R \ frac {\ text {d} q} {\ text {d} t} + \ gauche (\ frac {1} {c} \ droite) q $ (Equation 3)
En comparant l'équation 1 et l'équation 3, nous obtiendrons les quantités analogues du système mécanique de translation et du système électrique. Le tableau suivant montre ces quantités analogues.
| Système mécanique translationnel | Système électrique |
|---|---|
| Force (F) | Tension (V) |
| Masse (M) | Inductance (L) |
| Coefficient de frottement (B) | Résistance (R) |
| Constante de ressort (K) | Réciproque de capacité $ (\ frac {1} {c}) $ |
| Déplacement (x) | Charge (q) |
| Vitesse (v) | Actuel (i) |
De même, il existe une analogie de tension de couple pour les systèmes mécaniques rotatifs. Parlons maintenant de cette analogie.
Analogie de tension de couple
Dans cette analogie, les équations mathématiques de rotational mechanical system sont comparées aux équations de maillage du système électrique.
Le système mécanique de rotation est illustré dans la figure suivante.

L'équation de couple équilibré est
$$ T = T_j + T_b + T_k $$
$ \ Rightarrow T = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} + B \ frac {\ text {d} \ theta} {\ text {d} t} + k \ thêta $ (Equation 4)
En comparant l'équation 4 et l'équation 3, nous obtiendrons les quantités analogues de système mécanique de rotation et de système électrique. Le tableau suivant montre ces quantités analogues.
| Système mécanique de rotation | Système électrique |
|---|---|
| Couple (T) | Tension (V) |
| Moment d'inertie (J) | Inductance (L) |
| Coefficient de friction rotationnel (B) | Résistance (R) |
| Constante du ressort de torsion (K) | Réciproque de capacité $ (\ frac {1} {c}) $ |
| Déplacement angulaire (θ) | Charge (q) |
| Vitesse angulaire (ω) | Actuel (i) |
Analogie de courant de force
Dans l'analogie du courant de force, les équations mathématiques du translational mechanical system sont comparées aux équations nodales du système électrique.
Tenez compte du système électrique suivant, comme illustré dans la figure suivante. Ce circuit se compose d'une source de courant, d'une résistance, d'un inducteur et d'un condensateur. Tous ces éléments électriques sont connectés en parallèle.

L'équation nodale est
$ i = \ frac {V} {R} + \ frac {1} {L} \ int Vdt + C \ frac {\ text {d} V} {\ text {d} t} $ (Equation 5)
Remplacez, $ V = \ frac {\ text {d} \ Psi} {\ text {d} t} $ dans l'équation 5.
$$ i = \ frac {1} {R} \ frac {\ text {d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi + C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} $$
$ \ Rightarrow i = C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} + \ left (\ frac {1} {R} \ right) \ frac {\ text { d} \ Psi} {\ text {d} t} + \ gauche (\ frac {1} {L} \ droite) \ Psi $ (Equation 6)
En comparant l'équation 1 et l'équation 6, nous obtiendrons les quantités analogues du système mécanique de translation et du système électrique. Le tableau suivant montre ces quantités analogues.
| Système mécanique translationnel | Système électrique |
|---|---|
| Force (F) | Actuel (i) |
| Masse (M) | Capacité (C) |
| Coefficient de frottement (B) | Réciproque de résistance $ (\ frac {1} {R}) $ |
| Constante de ressort (K) | Réciproque d'inductance $ (\ frac {1} {L}) $ |
| Déplacement (x) | Flux magnétique (ψ) |
| Vitesse (v) | Tension (V) |
De même, il existe une analogie du courant de couple pour les systèmes mécaniques rotatifs. Parlons maintenant de cette analogie.
Analogie du courant de couple
Dans cette analogie, les équations mathématiques du rotational mechanical system sont comparées aux équations de maillage nodal du système électrique.
En comparant l'équation 4 et l'équation 6, nous obtiendrons les quantités analogues de système mécanique de rotation et de système électrique. Le tableau suivant montre ces quantités analogues.
| Système mécanique de rotation | Système électrique |
|---|---|
| Couple (T) | Actuel (i) |
| Moment d'inertie (J) | Capacité (C) |
| Coefficient de friction rotationnel (B) | Réciproque de résistance $ (\ frac {1} {R}) $ |
| Constante du ressort de torsion (K) | Réciproque d'inductance $ (\ frac {1} {L}) $ |
| Déplacement angulaire (θ) | Flux magnétique (ψ) |
| Vitesse angulaire (ω) | Tension (V) |
Dans ce chapitre, nous avons discuté des analogies électriques des systèmes mécaniques. Ces analogies sont utiles pour étudier et analyser le système non électrique comme le système mécanique à partir d'un système électrique analogue.