Modélisation des systèmes mécaniques
Dans ce chapitre, parlons de la differential equation modelingdes systèmes mécaniques. Il existe deux types de systèmes mécaniques en fonction du type de mouvement.
- Systèmes mécaniques translationnels
- Systèmes mécaniques rotatifs
Modélisation des systèmes mécaniques translationnels
Les systèmes mécaniques de translation se déplacent straight line. Ces systèmes se composent principalement de trois éléments de base. Ce sont la masse, le ressort et le dashpot ou l'amortisseur.
Si une force est appliquée à un système mécanique de translation, elle est alors opposée par des forces opposées dues à la masse, à l'élasticité et au frottement du système. Puisque la force appliquée et les forces opposées sont dans des directions opposées, la somme algébrique des forces agissant sur le système est nulle. Voyons maintenant la force opposée par ces trois éléments individuellement.
Masse
La masse est la propriété d'un corps qui stocke kinetic energy. Si une force est appliquée sur un corps ayant une masseM, alors il est opposé par une force opposée due à la masse. Cette force opposée est proportionnelle à l'accélération du corps. Supposons que l'élasticité et le frottement soient négligeables.

$$ F_m \ propto \: a $$
$$ \ Rightarrow F_m = Ma = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
$$ F = F_m = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
Où,
F est la force appliquée
Fm est la force opposée due à la masse
M est la masse
a est l'accélération
x est le déplacement
Printemps
Le printemps est un élément qui stocke potential energy. Si une force est appliquée sur le ressortK, alors il est opposé par une force opposée due à l'élasticité du ressort. Cette force opposée est proportionnelle au déplacement du ressort. Supposons que la masse et le frottement sont négligeables.

$$ F \ propto \: x $$
$$ \ Rightarrow F_k = Kx $$
$$ F = F_k = Kx $$
Où,
F est la force appliquée
Fk est la force opposée due à l'élasticité du ressort
K est la constante du ressort
x est le déplacement
Dashpot
Si une force est appliquée sur le dashpot B, alors il est opposé par une force opposée due à frictiondu dashpot. Cette force opposée est proportionnelle à la vitesse du corps. Supposons que la masse et l'élasticité soient négligeables.

$$ F_b \ propto \: \ nu $$
$$ \ Rightarrow F_b = B \ nu = B \ frac {\ text {d} x} {\ text {d} t} $$
$$ F = F_b = B \ frac {\ text {d} x} {\ text {d} t} $$
Où,
Fb est la force opposée due au frottement du dashpot
B est le coefficient de frottement
v est la vitesse
x est le déplacement
Modélisation des systèmes mécaniques de rotation
Les systèmes mécaniques de rotation se déplacent autour d'un axe fixe. Ces systèmes se composent principalement de trois éléments de base. Ce sontmoment of inertia, torsional spring et dashpot.
Si un couple est appliqué à un système mécanique en rotation, il est alors opposé par des couples opposés dus au moment d'inertie, à l'élasticité et au frottement du système. Le couple appliqué et les couples opposés étant dans des sens opposés, la somme algébrique des couples agissant sur le système est nulle. Voyons maintenant le couple opposé par ces trois éléments individuellement.
Moment d'inertie
Dans le système mécanique de translation, la masse stocke l'énergie cinétique. De même, dans un système mécanique rotatif, le moment d'inertie stockekinetic energy.
Si un couple est appliqué sur un corps ayant un moment d'inertie J, puis il s'oppose par un couple opposé dû au moment d'inertie. Ce couple opposé est proportionnel à l'accélération angulaire du corps. Supposons que l'élasticité et le frottement soient négligeables.

$$ T_j \ propto \: \ alpha $$
$$ \ Rightarrow T_j = J \ alpha = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
$$ T = T_j = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
Où,
T est le couple appliqué
Tj est le couple opposé dû au moment d'inertie
J est le moment d'inertie
α est l'accélération angulaire
θ est le déplacement angulaire
Ressort de torsion
Dans le système mécanique de translation, le ressort stocke l'énergie potentielle. De même, dans le système mécanique de rotation, les réserves de ressort de torsionpotential energy.
Si un couple est appliqué sur le ressort de torsion K, alors il est opposé par un couple opposé dû à l'élasticité du ressort de torsion. Ce couple opposé est proportionnel au déplacement angulaire du ressort de torsion. Supposons que le moment d'inertie et de frottement soit négligeable.
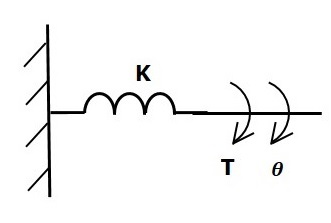
$$ T_k \ propto \: \ theta $$
$$ \ Rightarrow T_k = K \ theta $$
$$ T = T_k = K \ theta $$
Où,
T est le couple appliqué
Tk est le couple opposé dû à l'élasticité du ressort de torsion
K est la constante du ressort de torsion
θ est le déplacement angulaire
Dashpot
Si un couple est appliqué sur le dashpot B, puis il est opposé par un couple opposé dû au rotational frictiondu dashpot. Ce couple opposé est proportionnel à la vitesse angulaire du corps. Supposons que le moment d'inertie et l'élasticité soient négligeables.
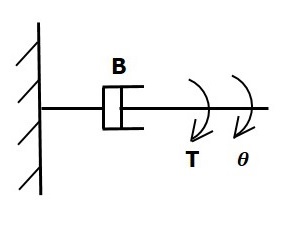
$$ T_b \ propto \: \ omega $$
$$ \ Rightarrow T_b = B \ omega = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
$$ T = T_b = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
Où,
Tb est le couple opposé dû au frottement en rotation du dashpot
B est le coefficient de frottement rotationnel
ω est la vitesse angulaire
θ est le déplacement angulaire