Systèmes de contrôle - Analyse du temps de réponse
Nous pouvons analyser la réponse des systèmes de contrôle à la fois dans le domaine temporel et dans le domaine fréquentiel. Nous discuterons de l'analyse de la réponse en fréquence des systèmes de contrôle dans les chapitres suivants. Parlons maintenant de l'analyse de la réponse temporelle des systèmes de contrôle.
Qu'est-ce que la réponse temporelle?
Si la sortie du système de contrôle pour une entrée varie en fonction du temps, alors on l'appelle le time responsedu système de contrôle. La réponse temporelle se compose de deux parties.
- Réponse transitoire
- Réponse en régime permanent
La réponse du système de commande dans le domaine temporel est illustrée dans la figure suivante.

Ici, les états transitoire et stable sont indiqués sur la figure. Les réponses correspondant à ces états sont appelées réponses transitoires et stables.
Mathématiquement, nous pouvons écrire la réponse temporelle c (t) comme
$$ c (t) = c_ {tr} (t) + c_ {ss} (t) $$
Où,
- c tr (t) est la réponse transitoire
- c ss (t) est la réponse en régime permanent
Réponse transitoire
Après avoir appliqué l'entrée au système de contrôle, la sortie prend un certain temps pour atteindre un état stable. Ainsi, la sortie sera dans un état transitoire jusqu'à ce qu'elle passe à un état stable. Par conséquent, la réponse du système de contrôle pendant l'état transitoire est appeléetransient response.
La réponse transitoire sera nulle pour les grandes valeurs de «t». Idéalement, cette valeur de «t» est l'infini et pratiquement, elle est cinq fois constante.
Mathématiquement, nous pouvons l'écrire comme
$$ \ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0 $$
Réponse en régime permanent
La partie de la réponse temporelle qui reste même après que la réponse transitoire a une valeur nulle pour les grandes valeurs de `` t '' est appelée steady state response. Cela signifie que la réponse transitoire sera nulle même en régime permanent.
Example
Trouvons les termes transitoire et stationnaire de la réponse temporelle du système de contrôle $ c (t) = 10 + 5e ^ {- t} $
Ici, le deuxième terme $ 5e ^ {- t} $ sera nul comme tdésigne l'infini. Donc, c'est letransient term. Et le premier terme 10 reste le mêmets'approche de l'infini. Donc, c'est lesteady state term.
Signaux de test standard
Les signaux de test standard sont impulsion, pas, rampe et parabolique. Ces signaux sont utilisés pour connaître les performances des systèmes de contrôle en utilisant la réponse temporelle de la sortie.
Signal d'impulsion de l'unité
Un signal d'impulsion unitaire, δ (t) est défini comme
$ \ delta (t) = 0 $ pour $ t \ neq 0 $
et $ \ int_ {0 ^ -} ^ {0 ^ +} \ delta (t) dt = 1 $
La figure suivante montre le signal d'impulsion de l'unité.

Ainsi, le signal d'impulsion unitaire n'existe que lorsque «t» est égal à zéro. La zone de ce signal sous un petit intervalle de temps autour de «t» est égale à zéro est un. La valeur du signal d'impulsion unitaire est égale à zéro pour toutes les autres valeurs de «t».
Signal de pas d'unité
Un signal de pas unitaire, u (t) est défini comme
$$ u (t) = 1; t \ geq 0 $$
$ = 0; t <0 $
La figure suivante montre le signal de pas d'unité.

Ainsi, le signal de pas unitaire existe pour toutes les valeurs positives de «t», y compris zéro. Et sa valeur est de un pendant cet intervalle. La valeur du signal de pas unitaire est zéro pour toutes les valeurs négatives de «t».
Signal de rampe de l'unité
Un signal de rampe unitaire, r (t) est défini comme
$$ r (t) = t; t \ geq 0 $$
$ = 0; t <0 $
Nous pouvons écrire le signal de rampe unitaire, $ r (t) $ en termes de signal de pas unitaire, $ u (t) $ comme
$$ r (t) = tu (t) $$
La figure suivante montre le signal de rampe de l'unité.

Ainsi, le signal de rampe d'unité existe pour toutes les valeurs positives de «t», y compris zéro. Et sa valeur augmente linéairement par rapport à «t» pendant cet intervalle. La valeur du signal de rampe unitaire est zéro pour toutes les valeurs négatives de «t».
Signal parabolique d'unité
Un signal parabolique unitaire, p (t) est défini comme,
$$ p (t) = \ frac {t ^ 2} {2}; t \ geq 0 $$
$ = 0; t <0 $
Nous pouvons écrire un signal parabolique unitaire, $ p (t) $ en termes de signal de pas unitaire, $ u (t) $ comme,
$$ p (t) = \ frac {t ^ 2} {2} u (t) $$
La figure suivante montre le signal parabolique de l'unité.
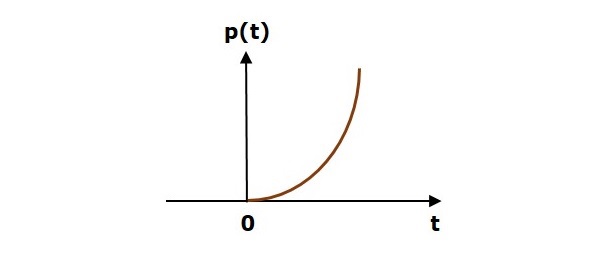
Ainsi, le signal parabolique unitaire existe pour toutes les valeurs positives de ‘t’y compris zéro. Et sa valeur augmente de manière non linéaire par rapport à «t» pendant cet intervalle. La valeur du signal parabolique unitaire est zéro pour toutes les valeurs négatives de «t».