Optimisation convexe - Minima et Maxima
Local Minima ou Minimize
$ \ bar {x} \ in \: S $ est dit minima locaux d'une fonction $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ où $ N_ \ varepsilon \ left (\ bar {x} \ right) $ signifie le voisinage de $ \ bar {x} $, soit $ N_ \ varepsilon \ left (\ bar {x} \ right) $ signifie $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $
Local Maxima ou Maximizer
$ \ bar {x} \ in \: S $ est dit être les maxima locaux d'une fonction $ f $ if $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ où $ N_ \ varepsilon \ left (\ bar {x} \ right) $ signifie le voisinage de $ \ bar {x} $, soit $ N_ \ varepsilon \ left (\ bar {x} \ right) $ signifie $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $
Minimums mondiaux
$ \ bar {x} \ in \: S $ est dit être des minima globaux d'une fonction $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ en S $
Maximas globaux
$ \ bar {x} \ in \: S $ est dit maximum global d'une fonction $ f $ if $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ en S $
Exemples
Step 1- trouver les minima et maxima locaux de $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ droite | $
Solution -

D'après le graphique de la fonction ci-dessus, il est clair que les minima locaux se produisent à $ x = \ pm 2 $ et les maxima locaux à $ x = 0 $
Step 2- trouver les minima globaux de la fonction $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ droite | $
Solution -
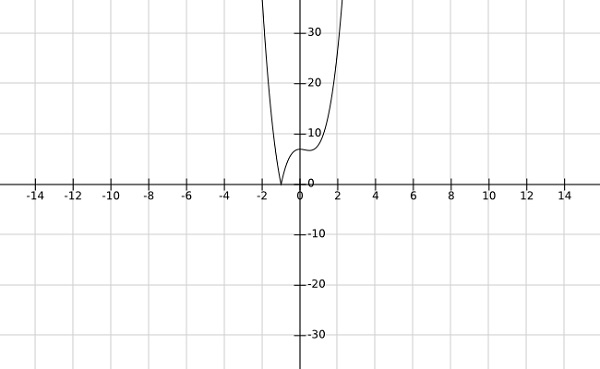
D'après le graphique de la fonction ci-dessus, il est clair que les minima globaux se produisent à $ x = -1 $.