Structures de données et algorithmes - Tableaux

Array est un conteneur qui peut contenir un nombre fixe d'éléments et ces éléments doivent être du même type. La plupart des structures de données utilisent des tableaux pour implémenter leurs algorithmes. Voici les termes importants pour comprendre le concept de Array.

• Element - Chaque élément stocké dans un tableau est appelé un élément.

• Index - Chaque emplacement d'un élément dans un tableau a un index numérique, qui est utilisé pour identifier l'élément.

Représentation du tableau

Les tableaux peuvent être déclarés de différentes manières dans différentes langues. Pour illustration, prenons la déclaration de tableau C.

Les tableaux peuvent être déclarés de différentes manières dans différentes langues. Pour illustration, prenons la déclaration de tableau C.

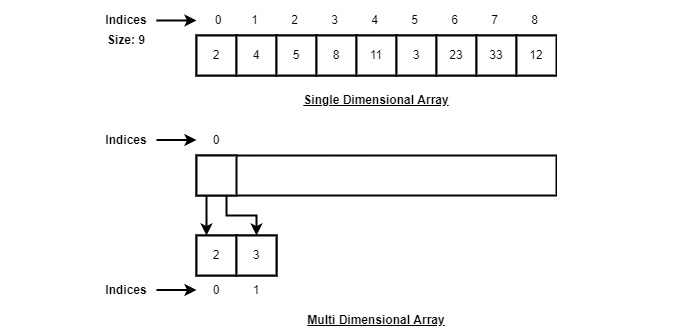
Conformément à l'illustration ci-dessus, voici les points importants à considérer.

• L'index commence par 0.

• La longueur du tableau est de 10, ce qui signifie qu'il peut stocker 10 éléments.

• Chaque élément est accessible via son index. Par exemple, nous pouvons récupérer un élément à l'index 6 comme 9.

Opérations de base

Voici les opérations de base prises en charge par une baie.

• Traverse - imprimer tous les éléments du tableau un par un.

• Insertion - Ajoute un élément à l'index donné.

• Deletion - Supprime un élément à l'index donné.

• Search - Recherche un élément en utilisant l'index donné ou par la valeur.

• Update - Met à jour un élément à l'index donné.

En C, lorsqu'un tableau est initialisé avec size, il attribue des valeurs par défaut à ses éléments dans l'ordre suivant.

Type de données	Valeur par défaut
booléen	faux
carboniser	0
int	0
flotte	0,0
double	0,0f
néant
wchar_t	0

Fonctionnement de la traversée

Cette opération consiste à parcourir les éléments d'un tableau.

Exemple

Le programme suivant parcourt et imprime les éléments d'un tableau:

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;   
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Lorsque nous compilons et exécutons le programme ci-dessus, il produit le résultat suivant -

Production

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8

Opération d'insertion

L'opération d'insertion consiste à insérer un ou plusieurs éléments de données dans un tableau. En fonction de l'exigence, un nouvel élément peut être ajouté au début, à la fin ou à tout index donné du tableau.

Ici, nous voyons une implémentation pratique de l'opération d'insertion, où nous ajoutons des données à la fin du tableau -

Exemple

Voici la mise en œuvre de l'algorithme ci-dessus -

#include <stdio.h>

main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   
   printf("The original array elements are :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }

   n = n + 1;
	
   while( j >= k) {
      LA[j+1] = LA[j];
      j = j - 1;
   }

   LA[k] = item;

   printf("The array elements after insertion :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Lorsque nous compilons et exécutons le programme ci-dessus, il produit le résultat suivant -

Production

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after insertion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 10 
LA[4] = 7 
LA[5] = 8

Pour d'autres variantes de l'opération d'insertion de tableau, cliquez ici

Opération de suppression

La suppression fait référence à la suppression d'un élément existant du tableau et à la réorganisation de tous les éléments d'un tableau.

Algorithme

Considérer LA est un tableau linéaire avec N éléments et K est un entier positif tel que K<=N. Voici l'algorithme pour supprimer un élément disponible à la K ^e position de LA.

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop

Exemple

Voici la mise en œuvre de l'algorithme ci-dessus -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   j = k;
	
   while( j < n) {
      LA[j-1] = LA[j];
      j = j + 1;
   }
	
   n = n -1;
   
   printf("The array elements after deletion :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Lorsque nous compilons et exécutons le programme ci-dessus, il produit le résultat suivant -

Production

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after deletion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 7 
LA[3] = 8

Opération de recherche

Vous pouvez effectuer une recherche d'un élément de tableau en fonction de sa valeur ou de son index.

Algorithme

Considérer LA est un tableau linéaire avec N éléments et K est un entier positif tel que K<=N. Voici l'algorithme pour trouver un élément avec une valeur de ITEM en utilisant la recherche séquentielle.

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

Exemple

Voici la mise en œuvre de l'algorithme ci-dessus -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   while( j < n){
      if( LA[j] == item ) {
         break;
      }
		
      j = j + 1;
   }
	
   printf("Found element %d at position %d\n", item, j+1);
}

Lorsque nous compilons et exécutons le programme ci-dessus, il produit le résultat suivant -

Production

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
Found element 5 at position 3

Opération de mise à jour

L'opération de mise à jour fait référence à la mise à jour d'un élément existant du tableau à un index donné.

Algorithme

Considérer LA est un tableau linéaire avec N éléments et K est un entier positif tel que K<=N. Voici l'algorithme pour mettre à jour un élément disponible à la K ^e position de LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop

Exemple

Voici la mise en œuvre de l'algorithme ci-dessus -

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   LA[k-1] = item;

   printf("The array elements after updation :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Lorsque nous compilons et exécutons le programme ci-dessus, il produit le résultat suivant -

Production

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after updation :
LA[0] = 1 
LA[1] = 3 
LA[2] = 10 
LA[3] = 7 
LA[4] = 8