Structures de données de tas
Le tas est un cas particulier de structure de données d'arborescence binaire équilibrée où la clé du nœud racine est comparée à ses enfants et arrangée en conséquence. Siα a un nœud enfant β puis -
touche (α) ≥ touche (β)
La valeur de parent étant supérieure à celle de child, cette propriété génère Max Heap. Sur la base de ces critères, un tas peut être de deux types -
For Input → 35 33 42 10 14 19 27 44 26 31Min-Heap - Où la valeur du nœud racine est inférieure ou égale à l'un de ses enfants.
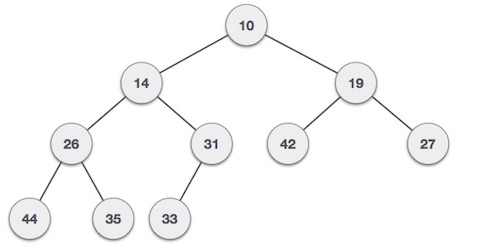
Max-Heap - Où la valeur du nœud racine est supérieure ou égale à l'un de ses enfants.

Les deux arbres sont construits en utilisant la même entrée et le même ordre d'arrivée.
Algorithme de construction de tas maximum
Nous utiliserons le même exemple pour montrer comment un Max Heap est créé. La procédure pour créer un tas min est similaire mais nous optons pour des valeurs min au lieu de valeurs max.
Nous allons dériver un algorithme pour le tas maximum en insérant un élément à la fois. À tout moment, le tas doit conserver sa propriété. Lors de l'insertion, nous supposons également que nous insérons un nœud dans une arborescence déjà remplie.
Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.Note - Dans l'algorithme de construction Min Heap, nous nous attendons à ce que la valeur du nœud parent soit inférieure à celle du nœud enfant.
Comprenons la construction de Max Heap par une illustration animée. Nous considérons le même échantillon d'entrée que nous avons utilisé précédemment.

Algorithme de suppression maximale du tas
Dérivons un algorithme pour supprimer du tas max. La suppression dans Max (ou Min) Heap se produit toujours à la racine pour supprimer la valeur Maximum (ou minimum).
Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.