Structure de données et algorithmes - Arbres AVL

Que faire si l'entrée de l'arbre de recherche binaire est triée (par ordre croissant ou décroissant)? Cela ressemblera alors à ceci -

On observe que les performances les plus défavorables de BST sont les plus proches des algorithmes de recherche linéaire, c'est-à-dire Ο (n). Dans les données en temps réel, nous ne pouvons pas prédire le modèle de données et leurs fréquences. Il est donc nécessaire d'équilibrer la BST existante.

Nommé d'après leur inventeur Adelson, Velski & Landis, AVL treessont un arbre de recherche binaire d'équilibrage de la hauteur. L'arbre AVL vérifie la hauteur des sous-arbres gauche et droit et assure que la différence n'est pas supérieure à 1. Cette différence est appeléeBalance Factor.

Ici, nous voyons que le premier arbre est équilibré et les deux suivants ne sont pas équilibrés -

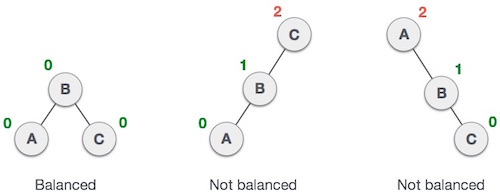
Dans le deuxième arbre, le sous-arbre gauche de C a la hauteur 2 et le sous-arbre droit a la hauteur 0, donc la différence est 2. Dans le troisième arbre, le sous-arbre droit de Aa la hauteur 2 et la gauche est manquante, donc c'est 0, et la différence est à nouveau 2. L'arbre AVL permet à la différence (facteur d'équilibre) d'être seulement 1.

BalanceFactor = height(left-sutree) − height(right-sutree)

Si la différence de hauteur des sous-arbres gauche et droit est supérieure à 1, l'arbre est équilibré en utilisant certaines techniques de rotation.

Rotations AVL

Pour s'équilibrer, un arbre AVL peut effectuer les quatre types de rotations suivants -

Rotation gauche
Rotation droite
Rotation gauche-droite
Rotation droite-gauche

Les deux premières rotations sont des rotations simples et les deux suivantes sont des rotations doubles. Pour avoir un arbre déséquilibré, il faut au moins un arbre de hauteur 2. Avec cet arbre simple, comprenons-les un par un.

Rotation gauche

Si un arbre devient déséquilibré, lorsqu'un nœud est inséré dans le sous-arbre droit du sous-arbre droit, nous effectuons une seule rotation à gauche -

Dans notre exemple, node Aest devenu déséquilibré lorsqu'un nœud est inséré dans le sous-arbre droit du sous-arbre droit de A. Nous effectuons la rotation gauche en faisantA le sous-arbre gauche de B.

Rotation à droite

L'arbre AVL peut devenir déséquilibré, si un nœud est inséré dans le sous-arbre gauche du sous-arbre gauche. L'arbre a alors besoin d'une bonne rotation.

Comme illustré, le nœud déséquilibré devient l'enfant droit de son enfant gauche en effectuant une rotation à droite.

Rotation gauche-droite

Les doubles rotations sont une version légèrement complexe des versions déjà expliquées des rotations. Pour mieux les comprendre, il faut prendre note de chaque action effectuée lors de la rotation. Voyons d'abord comment effectuer une rotation gauche-droite. Une rotation gauche-droite est une combinaison de rotation gauche suivie d'une rotation droite.

Etat	action
	Un nœud a été inséré dans le sous-arbre droit du sous-arbre gauche. Cela faitCun nœud déséquilibré. Ces scénarios amènent l'arborescence AVL à effectuer une rotation gauche-droite.
	Nous effectuons d'abord la rotation gauche sur le sous-arbre gauche de C. Cela faitA, le sous-arbre gauche de B.
	Nœud C est toujours déséquilibré, mais maintenant, c'est à cause du sous-arbre gauche du sous-arbre gauche.
	Nous allons maintenant faire pivoter l'arbre à droite, B le nouveau nœud racine de ce sous-arbre. C devient maintenant le sous-arbre droit de son propre sous-arbre gauche.
	L'arbre est maintenant équilibré.

Rotation droite-gauche

Le deuxième type de double rotation est la rotation droite-gauche. C'est une combinaison de rotation droite suivie d'une rotation gauche.

Etat	action
	Un nœud a été inséré dans le sous-arbre gauche du sous-arbre droit. Cela faitA, un nœud déséquilibré avec un facteur d'équilibre 2.
	Tout d'abord, nous effectuons la bonne rotation le long C nœud, création C le sous-arbre droit de son propre sous-arbre gauche B. Maintenant,B devient le bon sous-arbre de A.
	Nœud A est toujours déséquilibré à cause du sous-arbre droit de son sous-arbre droit et nécessite une rotation à gauche.
	Une rotation à gauche est effectuée en faisant B le nouveau nœud racine du sous-arbre. A devient le sous-arbre gauche de son sous-arbre droit B.
	L'arbre est maintenant équilibré.