Structures de données - Analyse asymptotique

L'analyse asymptotique d'un algorithme fait référence à la définition de la limite / cadrage mathématique de ses performances d'exécution. En utilisant une analyse asymptotique, nous pouvons très bien conclure le meilleur cas, le cas moyen et le pire des scénarios d'un algorithme.

L'analyse asymptotique est liée à l'entrée, c'est-à-dire que s'il n'y a pas d'entrée dans l'algorithme, elle est conclue pour fonctionner en temps constant. Hormis l '«entrée», tous les autres facteurs sont considérés comme constants.

L'analyse asymptotique fait référence au calcul du temps d'exécution de toute opération en unités mathématiques de calcul. Par exemple, le temps d'exécution d'une opération est calculé comme f (n) et peut être pour une autre opération, il est calculé comme g (n ² ). Cela signifie que le temps de fonctionnement de la première opération augmentera linéairement avec l'augmentation den et le temps de fonctionnement de la deuxième opération augmentera de façon exponentielle lorsque naugmente. De même, le temps d'exécution des deux opérations sera presque le même sin est significativement petit.

Habituellement, le temps requis par un algorithme relève de trois types -

Best Case - Temps minimum requis pour l'exécution du programme.
Average Case - Temps moyen requis pour l'exécution du programme.
Worst Case - Temps maximum requis pour l'exécution du programme.

Notations asymptotiques

Voici les notations asymptotiques couramment utilisées pour calculer la complexité du temps d'exécution d'un algorithme.

Ο Notation
Notation Ω
Notation θ

Big Oh Notation, Ο

La notation Ο (n) est la manière formelle d'exprimer la limite supérieure du temps d'exécution d'un algorithme. Il mesure la complexité temporelle du cas le plus défavorable ou la durée la plus longue qu'un algorithme peut prendre pour se terminer.

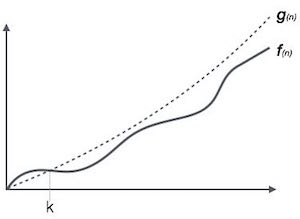
Par exemple, pour une fonction f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n₀ such that f(n) ≤ c.g(n) for all n > n₀. }

Notation oméga, Ω

La notation Ω (n) est la manière formelle d'exprimer la borne inférieure du temps d'exécution d'un algorithme. Il mesure la meilleure complexité temporelle du cas ou le meilleur temps qu'un algorithme peut prendre pour se terminer.

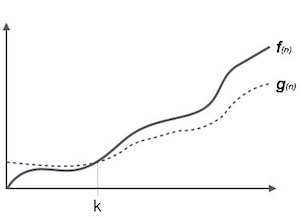
Par exemple, pour une fonction f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n₀ such that g(n) ≤ c.f(n) for all n > n₀. }

Notation thêta, θ

La notation θ (n) est la manière formelle d'exprimer à la fois la borne inférieure et la borne supérieure du temps d'exécution d'un algorithme. Il est représenté comme suit -

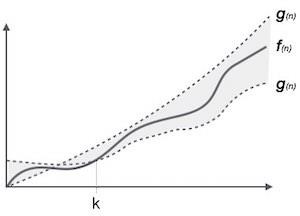
θ(f(n)) = { g(n) if and only if g(n) =  Ο(f(n)) and g(n) = Ω(f(n)) for all n > n₀. }

Notations asymptotiques courantes

Voici une liste de quelques notations asymptotiques courantes -

constant	-	Ο (1)
logarithmique	-	Ο (log n)
linéaire	-	Ο (n)
n log n	-	Ο (n log n)
quadratique	-	Ο (n ² )
cubique	-	Ο (n ³ )
polynôme	-	n ^{Ο (1)}
exponentiel	-	2 ^{Ο (n)}