Structures de données - Divisez pour conquérir
Dans l'approche de division pour conquérir, le problème en cours est divisé en sous-problèmes plus petits, puis chaque problème est résolu indépendamment. Lorsque nous continuons à diviser les sous-problèmes en sous-problèmes encore plus petits, nous pouvons éventuellement atteindre un stade où plus aucune division n'est possible. Ces plus petits sous-problèmes "atomiques" (fractions) sont résolus. La solution de tous les sous-problèmes est finalement fusionnée afin d'obtenir la solution d'un problème original.
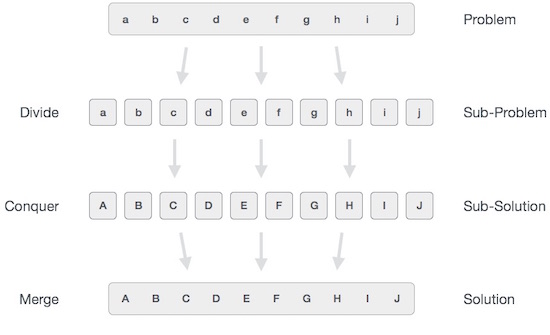
Globalement, nous pouvons comprendre divide-and-conquer approche dans un processus en trois étapes.
Diviser / Pause
Cette étape consiste à diviser le problème en sous-problèmes plus petits. Les sous-problèmes doivent représenter une partie du problème d'origine. Cette étape adopte généralement une approche récursive pour diviser le problème jusqu'à ce qu'aucun sous-problème ne soit davantage divisible. À ce stade, les sous-problèmes deviennent de nature atomique mais représentent encore une partie du problème réel.
Conquérir / Résoudre
Cette étape reçoit beaucoup de sous-problèmes plus petits à résoudre. Généralement, à ce niveau, les problèmes sont considérés comme «résolus» d'eux-mêmes.
Fusionner / Combiner
Lorsque les sous-problèmes plus petits sont résolus, cette étape les combine de manière récursive jusqu'à ce qu'ils formulent une solution du problème d'origine. Cette approche algorithmique fonctionne de manière récursive et les étapes de conquête et de fusion fonctionnent si étroitement qu'elles apparaissent comme une seule.
Exemples
Les algorithmes informatiques suivants sont basés sur divide-and-conquer approche de programmation -
- Tri par fusion
- Tri rapide
- Recherche binaire
- Multiplication matricielle de Strassen
- Paire la plus proche (points)
Il existe différentes façons de résoudre n'importe quel problème informatique, mais celles mentionnées sont un bon exemple d'approche de division pour conquérir.