Circuits numériques - Dé-multiplexeurs
De-Multiplexerest un circuit combinatoire qui effectue l'opération inverse du multiplexeur. Il a une seule entrée, «n» lignes de sélection et un maximum de 2 n sorties. L'entrée sera connectée à l'une de ces sorties en fonction des valeurs des lignes de sélection.
Puisqu'il y a 'n' lignes de sélection, il y aura 2 n combinaisons possibles de zéros et de uns. Ainsi, chaque combinaison ne peut sélectionner qu'une seule sortie. Le De-Multiplexer est également appeléDe-Mux.
Dé-multiplexeur 1x4
Le De-Multiplexer 1x4 a une entrée I, deux lignes de sélection, s 1 & s 0 et quatre sorties Y 3 , Y 2 , Y 1 et Y 0 . leblock diagram du De-Multiplexer 1x4 est illustré dans la figure suivante.

L'entrée unique «I» sera connectée à l'une des quatre sorties, Y 3 à Y 0 en fonction des valeurs des lignes de sélection s 1 et s0. leTruth table du De-Multiplexer 1x4 est illustré ci-dessous.
| Entrées de sélection | Les sorties | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
À partir du tableau de vérité ci-dessus, nous pouvons directement écrire le Boolean functions pour chaque sortie comme
$$ Y_ {3} = s_ {1} s_ {0} I $$
$$ Y_ {2} = s_ {1} {s_ {0}} 'I $$
$$ Y_ {1} = {s_ {1}} 's_ {0} I $$
$$ Y_ {0} = {s_1} '{s_ {0}}' I $$
Nous pouvons implémenter ces fonctions booléennes en utilisant des onduleurs et des portes ET à 3 entrées. lecircuit diagram du De-Multiplexer 1x4 est illustré dans la figure suivante.

Nous pouvons facilement comprendre le fonctionnement du circuit ci-dessus. De même, vous pouvez implémenter un De-Multiplexer 1x8 et 1x16 De-Multiplexer en suivant la même procédure.
Implémentation de dé-multiplexeurs d'ordre supérieur
Maintenant, implémentons les deux dé-multiplexeurs d'ordre supérieur suivants en utilisant des dé-multiplexeurs d'ordre inférieur.
- Dé-multiplexeur 1x8
- Dé-multiplexeur 1x16
Dé-multiplexeur 1x8
Dans cette section, implémentons le Dé-multiplexeur 1x8 à l'aide de Dé-multiplexeurs 1x4 et De-Multiplexeur 1x2. Nous savons que le De-Multiplexer 1x4 a une seule entrée, deux lignes de sélection et quatre sorties. Alors que le De-Multiplexer 1x8 a une seule entrée, trois lignes de sélection et huit sorties.
Donc, nous avons besoin de deux 1x4 De-Multiplexersdans la deuxième étape afin d'obtenir les huit derniers résultats. Puisque, le nombre d'entrées dans la deuxième étape est de deux, nous avons besoin1x2 DeMultiplexerdans le premier étage de sorte que les sorties du premier étage seront les entrées du deuxième étage. L'entrée de ce dé-multiplexeur 1x2 sera l'entrée globale du dé-multiplexeur 1x8.
Supposons que le De-Multiplexer 1x8 ait une entrée I, trois lignes de sélection s 2 , s 1 & s 0 et les sorties Y 7 à Y 0 . leTruth table du De-Multiplexer 1x8 est illustré ci-dessous.
| Entrées de sélection | Les sorties | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Nous pouvons implémenter facilement le De-Multiplexer 1x8 en utilisant des multiplexeurs d'ordre inférieur en considérant le tableau de vérité ci-dessus. leblock diagram du De-Multiplexer 1x8 est illustré dans la figure suivante.

Le commun selection lines, s1 & s0sont appliqués aux deux dé-multiplexeurs 1x4. Les sorties du De-Multiplexer 1x4 supérieur sont Y 7 à Y 4 et les sorties du De-Multiplexer 1x4 inférieur sont Y 3 à Y 0 .
L'autre selection line, s2est appliqué au De-Multiplexer 1x2. Si s 2 est égal à zéro, alors l'une des quatre sorties du De-Multiplexer 1x4 inférieur sera égale à l'entrée, I basée sur les valeurs des lignes de sélection s 1 et s 0 . De même, si s 2 est un, alors l'une des quatre sorties du DeMultiplexer 1x4 supérieur sera égale à l'entrée, I sur la base des valeurs des lignes de sélection s 1 et s 0 .
Dé-multiplexeur 1x16
Dans cette section, implémentons le De-Multiplexer 1x16 en utilisant 1x8 De-Multiplexers et 1x2 De-Multiplexer. Nous savons que le De-Multiplexer 1x8 a une seule entrée, trois lignes de sélection et huit sorties. Alors que le De-Multiplexer 1x16 a une seule entrée, quatre lignes de sélection et seize sorties.
Donc, nous avons besoin de deux 1x8 De-Multiplexersdans la deuxième étape afin d'obtenir les seize sorties finales. Puisque, le nombre d'entrées dans la deuxième étape est de deux, nous avons besoin1x2 DeMultiplexerdans le premier étage de sorte que les sorties du premier étage seront les entrées du deuxième étage. L'entrée de ce dé-multiplexeur 1x2 sera l'entrée globale du dé-multiplexeur 1x16.
Supposons que le De-Multiplexer 1x16 ait une entrée I, quatre lignes de sélection s 3 , s 2 , s 1 & s 0 et les sorties Y 15 à Y 0 . leblock diagram du De-Multiplexer 1x16 utilisant des multiplexeurs d'ordre inférieur est illustré dans la figure suivante.
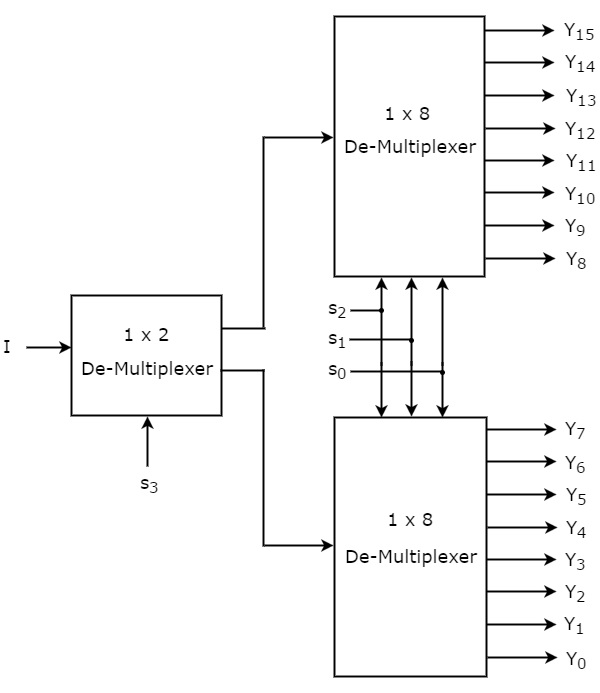
Le commun selection lines s2, s1 & s0sont appliqués aux deux dé-multiplexeurs 1x8. Les sorties du De-Multiplexer 1x8 supérieur sont Y 15 à Y 8 et les sorties du DeMultiplexer 1x8 inférieur sont Y 7 à Y 0 .
L'autre selection line, s3est appliqué au De-Multiplexer 1x2. Si s 3 est égal à zéro, alors l'une des huit sorties du De-Multiplexer 1x8 inférieur sera égale à l'entrée, I basée sur les valeurs des lignes de sélection s 2 , s 1 et s 0 . De même, si s3 est un, alors l'une des 8 sorties du De-Multiplexer 1x8 supérieur sera égale à l'entrée, I basée sur les valeurs des lignes de sélection s 2 , s 1 et s 0 .