Circuits numériques - Réalisation logique à deux niveaux
Le nombre maximum de niveaux présents entre les entrées et la sortie est de deux two level logic. Cela signifie que, quel que soit le nombre total de portes logiques, le nombre maximum de portes logiques présentes (en cascade) entre n'importe quelle entrée et sortie est de deux en logique à deux niveaux. Ici, les sorties des portes logiques de premier niveau sont connectées en tant qu'entrées de portes logiques de deuxième niveau.
Considérez les quatre portes logiques AND, OR, NAND & NOR. Puisqu'il y a 4 portes logiques, nous aurons 16 façons possibles de réaliser une logique à deux niveaux. Ce sont AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-OR, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND, NOR-OR, NOR-NAND, NOR-NOR.
Ces réalisations logiques à deux niveaux peuvent être classées dans les deux catégories suivantes.
- Forme dégénérative
- Forme non dégénérative
Forme dégénérative
Si la sortie de la réalisation logique à deux niveaux peut être obtenue en utilisant une seule porte logique, alors elle est appelée comme degenerative form. Évidemment, le nombre d'entrées d'une seule porte logique augmente. Pour cette raison, le fan-in de la porte logique augmente. C'est un avantage de la forme dégénérative.
Seulement 6 combinationsdes réalisations logiques à deux niveaux sur 16 combinaisons se présentent sous forme dégénérative. Ce sont AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND.
Dans cette section, parlons de quelques réalisations. Supposons que A, B, C et D sont les entrées et Y est la sortie dans chaque réalisation logique.
AND-AND Logic
Dans cette réalisation logique, les portes ET sont présentes dans les deux niveaux. La figure ci-dessous montre un exemple pourAND-AND logic la concrétisation.

Nous obtiendrons les sorties des portes logiques de premier niveau comme $ Y_ {1} = AB $ et $ Y_ {2} = CD $
Ces sorties, $ Y_ {1} $ et $ Y_ {2} $ sont appliquées comme entrées de la porte ET qui est présente au deuxième niveau. Ainsi, la sortie de cette porte ET est
$$ Y = Y_ {1} Y_ {2} $$
Remplacez les valeurs $ Y_ {1} $ et $ Y_ {2} $ dans l'équation ci-dessus.
$$ Y = \ gauche (AB \ droite) \ gauche (CD \ droite) $$
$ \ Flèche droite Y = ABCD $
Par conséquent, la sortie de cette réalisation logique ET-ET est ABCD. Cette fonction booléenne peut être implémentée en utilisant une porte ET à 4 entrées. Par conséquent, c'estdegenerative form.
Logique AND-NAND
Dans cette réalisation logique, les portes ET sont présentes au premier niveau et les portes NAND sont présentes au deuxième niveau. La figure suivante montre un exemple deAND-NAND logic la concrétisation.
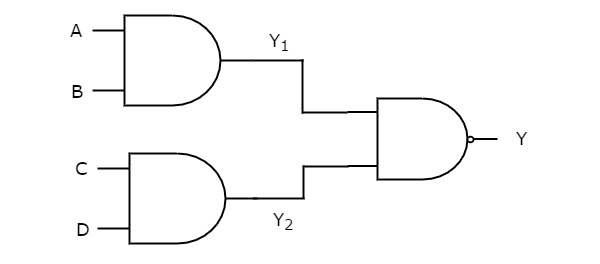
Auparavant, nous obtenions les sorties des portes logiques de premier niveau comme $ Y_ {1} = AB $ et $ Y_ {2} = CD $
Ces sorties, $ Y_ {1} $ et $ Y_ {2} $ sont appliquées comme entrées de la porte NAND qui est présente au deuxième niveau. Ainsi, la sortie de cette porte NAND est
$$ Y = {\ gauche (Y_ {1} Y_ {2} \ droite)} '$$
Remplacez les valeurs $ Y_ {1} $ et $ Y_ {2} $ dans l'équation ci-dessus.
$$ Y = {\ gauche (\ gauche (AB \ droite) \ gauche (CD \ droite) \ droite)} '$$
$ \ Rightarrow Y = {\ gauche (ABCD \ droite)} '$
Par conséquent, la sortie de cette réalisation logique AND-NAND est $ {\ left (ABCD \ right)} '$. Cette fonction booléenne peut être implémentée en utilisant une porte NAND à 4 entrées. Par conséquent, c'estdegenerative form.
Logique OR-OR
Dans cette réalisation logique, les portes OU sont présentes dans les deux niveaux. La figure suivante montre un exemple deOR-OR logic la concrétisation.
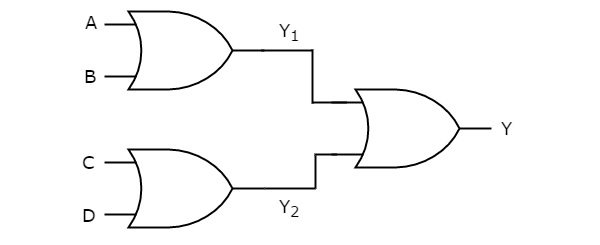
Nous obtiendrons les sorties des portes logiques de premier niveau comme $ Y_ {1} = A + B $ et $ Y_ {2} = C + D $.
Ces sorties, $ Y_ {1} $ et $ Y_ {2} $ sont appliquées comme entrées de la porte OU qui est présente au deuxième niveau. Ainsi, la sortie de cette porte OU est
$$ Y = Y_ {1} + Y_ {2} $$
Remplacez les valeurs $ Y_ {1} $ et $ Y_ {2} $ dans l'équation ci-dessus.
$$ Y = \ gauche (A + B \ droite) + \ gauche (C + D \ droite) $$
$ \ Flèche droite Y = A + B + C + D $
Par conséquent, la sortie de cette réalisation logique OU-OU est A+B+C+D. Cette fonction booléenne peut être implémentée en utilisant une porte OU à 4 entrées. Par conséquent, c'estdegenerative form.
De même, vous pouvez vérifier si les réalisations restantes appartiennent ou non à cette catégorie.
Forme non dégénérative
Si la sortie de la réalisation logique à deux niveaux ne peut pas être obtenue en utilisant une porte logique unique, alors elle est appelée comme non-degenerative form.
Le reste 10 combinationsdes réalisations logiques à deux niveaux se présentent sous forme non dégénérative. Ce sont AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR.
Maintenant, laissez-nous discuter de quelques réalisations. Supposons que A, B, C et D sont les entrées et Y est la sortie dans chaque réalisation logique.
Logique AND-OR
Dans cette réalisation logique, les portes ET sont présentes au premier niveau et les portes OU sont présentes au deuxième niveau. La figure ci-dessous montre un exemple pourAND-OR logic la concrétisation.

Auparavant, nous obtenions les sorties des portes logiques de premier niveau comme $ Y_ {1} = AB $ et $ Y_ {2} = CD $.
Ces sorties Y1 et Y2 sont appliquées en tant qu'entrées de la porte OU qui est présente au deuxième niveau. Ainsi, la sortie de cette porte OU est
$$ Y = Y_ {1} + Y_ {2} $$
Remplacez les valeurs $ Y_ {1} $ et $ Y_ {2} $ dans l'équation ci-dessus
$$ Y = AB + CD $$
Par conséquent, la sortie de cette réalisation logique ET-OU est AB+CD. Cette fonction booléenne est enSum of Productsforme. Puisque nous ne pouvons pas l'implémenter en utilisant une seule porte logique, cette réalisation logique ET-OU est unnon-degenerative form.
Logique AND-NOR
Dans cette réalisation logique, les portes ET sont présentes au premier niveau et la ou les portes NOR sont présentes au deuxième niveau. La figure suivante montre un exemple deAND-NOR logic la concrétisation.

Nous connaissons les sorties des portes logiques de premier niveau comme $ Y_ {1} = AB $ et $ Y_ {2} = CD $
Ces sorties Y1 et Y2 sont appliquées en tant qu'entrées de la porte NOR qui est présente au deuxième niveau. Ainsi, la sortie de cette porte NOR est
$$ Y = {\ gauche (Y_ {1} + Y_ {2} \ droite)} '$$
Remplacez les valeurs $ Y_ {1} $ et $ Y_ {2} $ dans l'équation ci-dessus.
$$ Y = {\ gauche (AB + CD \ droite)} '$$
Par conséquent, la sortie de cette réalisation logique AND-NOR est $ {\ left (AB + CD \ right)} '$. Cette fonction booléenne est enAND-OR-Invertforme. Puisque nous ne pouvons pas l'implémenter en utilisant une seule porte logique, cette réalisation logique AND-NOR est unnon-degenerative form
OR-AND logique
Dans cette réalisation logique, les portes OU sont présentes au premier niveau et les portes ET sont présentes au deuxième niveau. La figure suivante montre un exemple deOR-AND logic la concrétisation.

Auparavant, nous obtenions les sorties des portes logiques de premier niveau comme $ Y_ {1} = A + B $ et $ Y_ {2} = C + D $.
Ces sorties, $ Y_ {1} $ et $ Y_ {2} $ sont appliquées comme entrées de la porte ET qui est présente au deuxième niveau. Ainsi, la sortie de cette porte ET est
$$ Y = Y_ {1} Y_ {2} $$
Remplacez les valeurs $ Y_ {1} $ et $ Y_ {2} $ dans l'équation ci-dessus.
$$ Y = \ gauche (A + B \ droite) \ gauche (C + D \ droite) $$
Par conséquent, la sortie de cette réalisation logique OU-ET est (A + B) (C + D). Cette fonction booléenne est enProduct of Sumsforme. Puisque nous ne pouvons pas l'implémenter en utilisant une seule porte logique, cette réalisation logique OU-ET est unnon-degenerative form.
De même, vous pouvez vérifier si les réalisations restantes appartiennent ou non à cette catégorie.